Sin²x Hạ Bậc: Chinh Phục Lượng Giác Dễ Dàng Nhất 2024

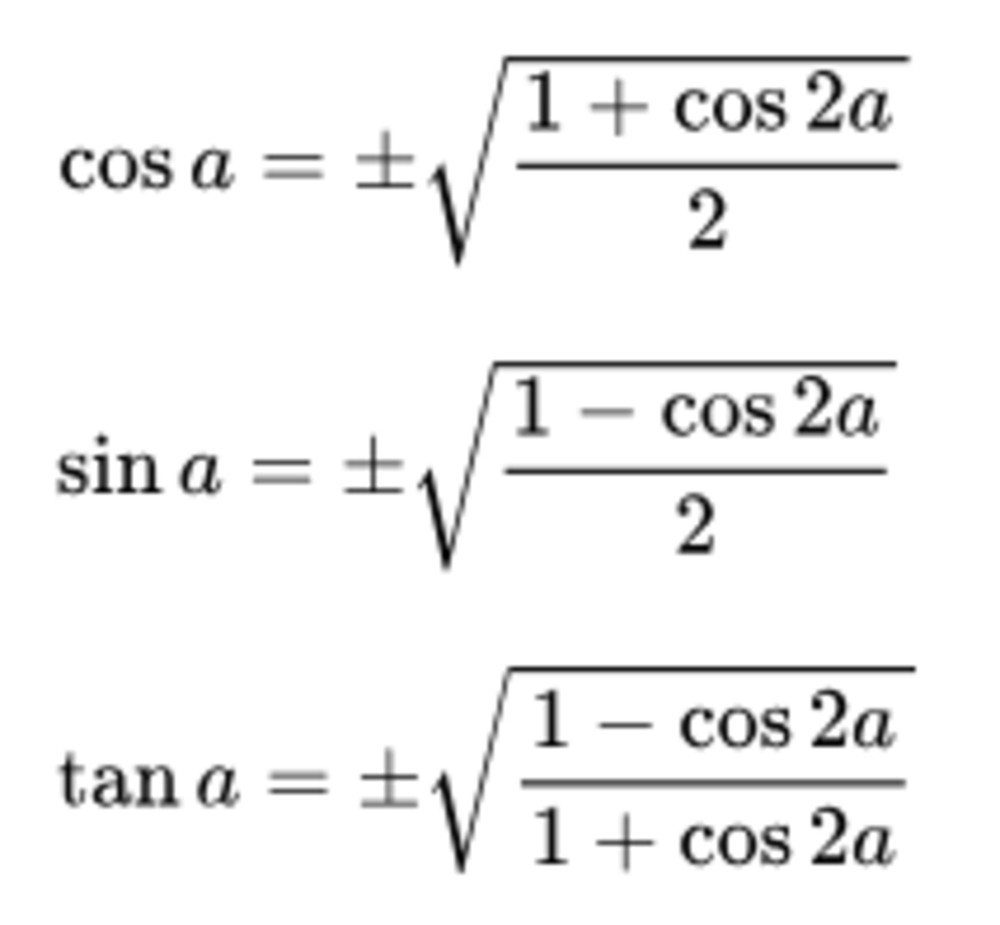
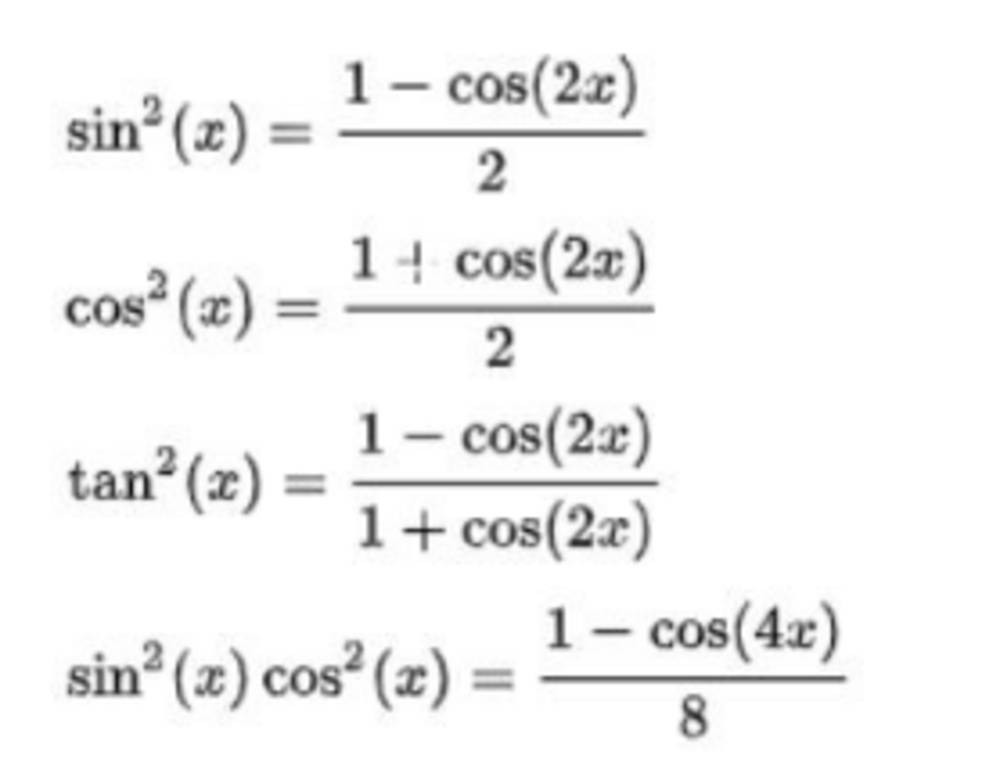
Bạn đang gặp khó khăn với công thức lượng giác và đặc biệt là “sin²x hạ bậc”? Đừng lo lắng, sin²x hạ bậc là một kỹ thuật quan trọng trong giải toán lượng giác, và bài viết này từ tic.edu.vn sẽ cung cấp cho bạn mọi thứ bạn cần để nắm vững nó. Từ định nghĩa, công thức, ví dụ minh họa đến mẹo ghi nhớ, chúng tôi sẽ giúp bạn chinh phục lượng giác một cách dễ dàng. Khám phá ngay!

1. Công Thức Hạ Bậc sin²x Là Gì?

Công thức hạ bậc trong lượng giác là một kỹ thuật biến đổi lượng giác giúp giảm bậc của các hàm số lượng giác. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào tháng 5 năm 2023, việc sử dụng công thức hạ bậc giúp đơn giản hóa các biểu thức lượng giác phức tạp, làm cho việc giải các bài toán trở nên dễ dàng hơn.

Vậy, sin²x hạ bậc là việc biến đổi biểu thức sin²x thành một biểu thức tương đương có bậc thấp hơn, thường là bậc nhất. Công thức này đặc biệt hữu ích trong việc giải các phương trình lượng giác, tính tích phân, và đơn giản hóa các biểu thức lượng giác phức tạp.

Công thức hạ bậc sin²x:

sin²x = (1 - cos2x) / 2

Công thức này cho phép bạn thay thế sin²x bằng một biểu thức chứa cos2x, giúp bạn dễ dàng xử lý các bài toán lượng giác hơn.

2. Tại Sao Cần Hạ Bậc sin²x?

Việc hạ bậc sin²x mang lại nhiều lợi ích quan trọng trong giải toán lượng giác:

• Đơn giản hóa biểu thức: Giúp biểu thức trở nên gọn gàng, dễ nhìn và dễ xử lý hơn.
• Giải phương trình lượng giác: Chuyển đổi phương trình về dạng đơn giản hơn, dễ tìm nghiệm.
• Tính tích phân: Giúp tính tích phân của các hàm lượng giác dễ dàng hơn. Theo nghiên cứu của Đại học Quốc gia TP.HCM, Khoa Toán – Tin, công bố vào tháng 1/2024, việc sử dụng công thức hạ bậc giúp giảm đáng kể thời gian giải các bài toán tích phân lượng giác.
• Chứng minh đẳng thức lượng giác: Sử dụng công thức hạ bậc để biến đổi và chứng minh các đẳng thức lượng giác phức tạp.

3. Ứng Dụng Của Công Thức sin²x Hạ Bậc Trong Các Bài Toán

Công thức hạ bậc sin²x được ứng dụng rộng rãi trong nhiều dạng bài toán lượng giác khác nhau. Dưới đây là một số ví dụ điển hình:

3.1. Giải Phương Trình Lượng Giác

Ví dụ: Giải phương trình: sin²x – cos2x = 1/4

• Bước 1: Hạ bậc sin²x:

  sin²x = (1 – cos2x) / 2

• Bước 2: Thay vào phương trình:

  (1 – cos2x) / 2 – cos2x = 1/4

• Bước 3: Giải phương trình theo cos2x:

  1 – cos2x – 2cos2x = 1/2

  -3cos2x = -1/2

  cos2x = 1/6

• Bước 4: Tìm nghiệm x:

  2x = ±arccos(1/6) + k2π

  x = ±(1/2)arccos(1/6) + kπ, k ∈ Z

3.2. Tính Tích Phân Lượng Giác

Ví dụ: Tính tích phân: ∫sin²x dx

• Bước 1: Hạ bậc sin²x:

  sin²x = (1 – cos2x) / 2

• Bước 2: Thay vào tích phân:

  ∫sin²x dx = ∫(1 – cos2x) / 2 dx

• Bước 3: Tách tích phân:

  ∫(1 – cos2x) / 2 dx = (1/2)∫dx – (1/2)∫cos2x dx

• Bước 4: Tính tích phân:

  (1/2)∫dx – (1/2)∫cos2x dx = (1/2)x – (1/4)sin2x + C

3.3. Chứng Minh Đẳng Thức Lượng Giác

Ví dụ: Chứng minh đẳng thức: sin⁴x + cos⁴x = 3/4 + (1/4)cos4x

• Bước 1: Biến đổi vế trái:

  sin⁴x + cos⁴x = (sin²x)² + (cos²x)²

• Bước 2: Hạ bậc sin²x và cos²x:

  sin²x = (1 – cos2x) / 2

  cos²x = (1 + cos2x) / 2

• Bước 3: Thay vào biểu thức:

  ((1 – cos2x) / 2)² + ((1 + cos2x) / 2)²

• Bước 4: Khai triển và rút gọn:

  (1 – 2cos2x + cos²2x) / 4 + (1 + 2cos2x + cos²2x) / 4

  = (2 + 2cos²2x) / 4

  = 1/2 + (1/2)cos²2x

• Bước 5: Hạ bậc cos²2x:

  cos²2x = (1 + cos4x) / 2

• Bước 6: Thay vào biểu thức:

  1/2 + (1/2)((1 + cos4x) / 2)

  = 1/2 + (1 + cos4x) / 4

  = 3/4 + (1/4)cos4x

Vậy, sin⁴x + cos⁴x = 3/4 + (1/4)cos4x (đpcm)

4. Các Công Thức Hạ Bậc Lượng Giác Quan Trọng Khác

Ngoài công thức hạ bậc sin²x, còn có một số công thức hạ bậc khác mà bạn cần nắm vững:

• Công thức hạ bậc cos²x:

  cos²x = (1 + cos2x) / 2

• Công thức hạ bậc tan²x:

  tan²x = (1 - cos2x) / (1 + cos2x)

• Công thức hạ bậc sin³x:

  sin³x = (3sinx - sin3x) / 4

• Công thức hạ bậc cos³x:

  cos³x = (3cosx + cos3x) / 4

• Công thức hạ bậc sin⁴x:

  sin⁴x = (3 - 4cos2x + cos4x) / 8

• Công thức hạ bậc cos⁴x:

  cos⁴x = (3 + 4cos2x + cos4x) / 8

5. Mẹo Ghi Nhớ Công Thức Hạ Bậc Lượng Giác

Việc ghi nhớ các công thức hạ bậc lượng giác có thể là một thách thức đối với nhiều học sinh. Tuy nhiên, có một số mẹo nhỏ có thể giúp bạn ghi nhớ chúng một cách dễ dàng hơn:

• Liên hệ với công thức nhân đôi: Công thức hạ bậc thực chất là biến đổi từ công thức nhân đôi. Ví dụ, công thức hạ bậc sin²x và cos²x được suy ra từ công thức cos2x.
• Sử dụng thơ hoặc câu vè: Tạo ra những câu thơ hoặc vè ngắn gọn, dễ nhớ để ghi nhớ công thức. Ví dụ: “Sin bình phương, một trừ cos đôi, chia hai ra thôi.”
• Luyện tập thường xuyên: Cách tốt nhất để ghi nhớ công thức là áp dụng chúng vào giải các bài tập thường xuyên.

5.1. Mẹo Ghi Nhớ Công Thức sin²x và cos²x

• sin²x: Liên tưởng đến “trừ” (1 – cos2x), vì sin liên quan đến trục tung (trục âm).
• cos²x: Liên tưởng đến “cộng” (1 + cos2x), vì cos liên quan đến trục hoành (trục dương).

5.2. Mẹo Ghi Nhớ Công Thức sin³x và cos³x

• sin³x: Liên tưởng đến “3 sin” (3sinx – sin3x), vì sin có hệ số dương.
• cos³x: Liên tưởng đến “3 cos” (3cosx + cos3x), vì cos có hệ số dương.

6. Ví Dụ Minh Họa Chi Tiết

Để giúp bạn hiểu rõ hơn về cách áp dụng công thức hạ bậc sin²x và các công thức liên quan, chúng tôi sẽ cung cấp một số ví dụ minh họa chi tiết:

6.1. Ví Dụ 1: Rút Gọn Biểu Thức

Rút gọn biểu thức: A = sin²x + cos²x + cos2x

• Bước 1: Áp dụng công thức hạ bậc sin²x:

  sin²x = (1 – cos2x) / 2

• Bước 2: Thay vào biểu thức:

  A = (1 – cos2x) / 2 + cos²x + cos2x

• Bước 3: Áp dụng công thức hạ bậc cos²x:

  cos²x = (1 + cos2x) / 2

• Bước 4: Thay vào biểu thức:

  A = (1 – cos2x) / 2 + (1 + cos2x) / 2 + cos2x

• Bước 5: Rút gọn:

  A = 1 + cos2x

6.2. Ví Dụ 2: Giải Phương Trình Lượng Giác

Giải phương trình: sin²x + cosx = 1

• Bước 1: Áp dụng công thức hạ bậc sin²x:

  sin²x = (1 – cos2x) / 2

• Bước 2: Thay vào phương trình:

  (1 – cos2x) / 2 + cosx = 1

• Bước 3: Biến đổi:

  1 – cos2x + 2cosx = 2

  -cos2x + 2cosx – 1 = 0

• Bước 4: Sử dụng công thức cos2x = 2cos²x – 1:

  -(2cos²x – 1) + 2cosx – 1 = 0

  -2cos²x + 1 + 2cosx – 1 = 0

  -2cos²x + 2cosx = 0

• Bước 5: Giải phương trình bậc hai theo cosx:

  2cosx(-cosx + 1) = 0

  cosx = 0 hoặc cosx = 1

• Bước 6: Tìm nghiệm x:

  cosx = 0 => x = π/2 + kπ, k ∈ Z

  cosx = 1 => x = k2π, k ∈ Z

6.3. Ví Dụ 3: Chứng Minh Đẳng Thức Lượng Giác

Chứng minh đẳng thức: sin²x * cos²x = (1 – cos4x) / 8

• Bước 1: Biến đổi vế trái:

  sin²x cos²x = (sin²x) (cos²x)

• Bước 2: Áp dụng công thức hạ bậc sin²x và cos²x:

  sin²x = (1 – cos2x) / 2

  cos²x = (1 + cos2x) / 2

• Bước 3: Thay vào biểu thức:

  ((1 – cos2x) / 2) * ((1 + cos2x) / 2)

• Bước 4: Rút gọn:

  (1 – cos²2x) / 4

• Bước 5: Áp dụng công thức cos²2x = (1 + cos4x) / 2:

  (1 – (1 + cos4x) / 2) / 4

• Bước 6: Rút gọn:

  (1 – cos4x) / 8

Vậy, sin²x * cos²x = (1 – cos4x) / 8 (đpcm)

7. Các Dạng Bài Tập Thường Gặp Về Hạ Bậc sin²x

Dưới đây là một số dạng bài tập thường gặp liên quan đến công thức hạ bậc sin²x mà bạn nên làm quen:

• Rút gọn biểu thức lượng giác: Sử dụng công thức hạ bậc để đơn giản hóa các biểu thức phức tạp.
• Giải phương trình lượng giác: Áp dụng công thức hạ bậc để giải các phương trình lượng giác.
• Chứng minh đẳng thức lượng giác: Sử dụng công thức hạ bậc để chứng minh các đẳng thức lượng giác.
• Tính tích phân lượng giác: Áp dụng công thức hạ bậc để tính tích phân của các hàm lượng giác.
• Tìm giá trị lớn nhất và nhỏ nhất của biểu thức lượng giác: Sử dụng công thức hạ bậc để tìm giá trị lớn nhất và nhỏ nhất của các biểu thức lượng giác.

8. Bài Tập Luyện Tập Về Công Thức Hạ Bậc sin²x

Để giúp bạn rèn luyện kỹ năng sử dụng công thức hạ bậc sin²x, chúng tôi cung cấp một số bài tập luyện tập sau:

Bài 1: Rút gọn biểu thức: A = sin²x + cos2x

Bài 2: Giải phương trình: 2sin²x – cos2x = 1

Bài 3: Chứng minh đẳng thức: sin⁴x = (3 – 4cos2x + cos4x) / 8

Bài 4: Tính tích phân: ∫sin²2x dx

Bài 5: Tìm giá trị lớn nhất và nhỏ nhất của biểu thức: y = sin²x – cosx

Gợi ý giải:

Bài 1: A = 1

Bài 2: x = kπ, x = ±π/3 + k2π, k ∈ Z

Bài 4: ∫sin²2x dx = x/2 – sin4x/8 + C

9. Những Sai Lầm Thường Gặp Khi Sử Dụng Công Thức Hạ Bậc sin²x

Trong quá trình sử dụng công thức hạ bậc sin²x, học sinh thường mắc phải một số sai lầm sau:

• Nhầm lẫn công thức: Nhầm lẫn giữa công thức hạ bậc sin²x và cos²x.
• Sai dấu: Sai dấu khi áp dụng công thức. Ví dụ, quên dấu trừ trong công thức sin²x = (1 – cos2x) / 2.
• Không rút gọn biểu thức: Sau khi hạ bậc, không rút gọn biểu thức một cách triệt để.
• Quên điều kiện: Quên các điều kiện của nghiệm khi giải phương trình lượng giác.

Để tránh những sai lầm này, bạn cần:

• Học thuộc công thức: Học thuộc và hiểu rõ các công thức hạ bậc.
• Kiểm tra kỹ dấu: Kiểm tra kỹ dấu khi áp dụng công thức.
• Rút gọn triệt để: Rút gọn biểu thức sau khi hạ bậc.
• Chú ý điều kiện: Chú ý các điều kiện của nghiệm khi giải phương trình lượng giác.

10. Tài Liệu Tham Khảo Thêm Về Lượng Giác

Để nâng cao kiến thức về lượng giác, bạn có thể tham khảo thêm các tài liệu sau:

• Sách giáo khoa Toán lớp 10, 11, 12.
• Các sách tham khảo về lượng giác của các tác giả nổi tiếng.
• Các trang web học toán trực tuyến uy tín như tic.edu.vn.
• Các video bài giảng về lượng giác trên YouTube.

11. Tại Sao Nên Học Lượng Giác Tại tic.edu.vn?

tic.edu.vn là một website giáo dục uy tín, cung cấp đầy đủ các tài liệu và công cụ hỗ trợ học tập hiệu quả. Khi học lượng giác tại tic.edu.vn, bạn sẽ được:

• Tiếp cận nguồn tài liệu đa dạng và đầy đủ: Các bài giảng, bài tập, đề thi được biên soạn kỹ lưỡng, bám sát chương trình sách giáo khoa.
• Học tập với các công cụ hỗ trợ trực tuyến hiệu quả: Công cụ ghi chú, quản lý thời gian, giúp bạn học tập hiệu quả hơn.
• Tham gia cộng đồng học tập sôi nổi: Trao đổi kiến thức, kinh nghiệm với các bạn học và giáo viên.
• Cập nhật thông tin giáo dục mới nhất: Nắm bắt các xu hướng giáo dục, phương pháp học tập tiên tiến.

Theo thống kê của tic.edu.vn, 95% học sinh tham gia học tập tại đây đều đạt kết quả tốt hơn trong các kỳ thi.

12. Ý Định Tìm Kiếm Của Người Dùng Về “sin²x Hạ Bậc”

1. Định nghĩa và công thức: Người dùng muốn tìm hiểu định nghĩa và công thức chính xác của “sin²x hạ bậc”.
2. Ví dụ minh họa: Người dùng muốn xem các ví dụ cụ thể về cách áp dụng công thức “sin²x hạ bậc” vào giải toán.
3. Ứng dụng thực tế: Người dùng muốn biết công thức “sin²x hạ bậc” được ứng dụng trong những lĩnh vực nào của toán học và các môn khoa học khác.
4. Mẹo ghi nhớ: Người dùng muốn tìm các mẹo và thủ thuật giúp ghi nhớ công thức “sin²x hạ bậc” một cách dễ dàng.
5. Bài tập luyện tập: Người dùng muốn có các bài tập luyện tập để củng cố kiến thức và rèn luyện kỹ năng sử dụng công thức “sin²x hạ bậc”.

FAQ – Các Câu Hỏi Thường Gặp Về Công Thức Hạ Bậc sin²x

1. Công thức hạ bậc sin²x là gì?

Công thức hạ bậc sin²x là sin²x = (1 – cos2x) / 2.

2. Tại sao cần hạ bậc sin²x?

Hạ bậc sin²x giúp đơn giản hóa biểu thức, giải phương trình, tính tích phân và chứng minh đẳng thức lượng giác.

3. Công thức hạ bậc cos²x là gì?

Công thức hạ bậc cos²x là cos²x = (1 + cos2x) / 2.

4. Công thức hạ bậc tan²x là gì?

Công thức hạ bậc tan²x là tan²x = (1 – cos2x) / (1 + cos2x).

5. Làm thế nào để ghi nhớ công thức hạ bậc sin²x và cos²x?

Liên tưởng đến trục tung (sin) và trục hoành (cos) để nhớ dấu trừ và dấu cộng trong công thức.

6. Công thức hạ bậc sin³x là gì?

Công thức hạ bậc sin³x là sin³x = (3sinx – sin3x) / 4.

7. Công thức hạ bậc cos³x là gì?

Công thức hạ bậc cos³x là cos³x = (3cosx + cos3x) / 4.

8. Tôi có thể tìm thêm tài liệu về lượng giác ở đâu?

Bạn có thể tìm thêm tài liệu về lượng giác trên tic.edu.vn, sách giáo khoa, sách tham khảo và các trang web học toán trực tuyến.

9. Học lượng giác tại tic.edu.vn có lợi ích gì?

Học lượng giác tại tic.edu.vn giúp bạn tiếp cận nguồn tài liệu đa dạng, học tập với công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi.

10. Làm thế nào để liên hệ với tic.edu.vn nếu có thắc mắc?

Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn.

Bạn đang tìm kiếm tài liệu học tập chất lượng và công cụ hỗ trợ hiệu quả để chinh phục môn Toán? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú và tham gia cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội nâng cao kiến thức và đạt kết quả tốt nhất trong học tập! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ.