Phương Trình Đường Tròn: Bí Quyết Chinh Phục Mọi Bài Toán

Phương trình đường tròn là một trong những kiến thức quan trọng trong chương trình toán học phổ thông. Bạn đang gặp khó khăn trong việc giải các bài toán liên quan đến phương trình đường tròn? Hãy để tic.edu.vn đồng hành cùng bạn, cung cấp những kiến thức và công cụ cần thiết để bạn chinh phục mọi thử thách.

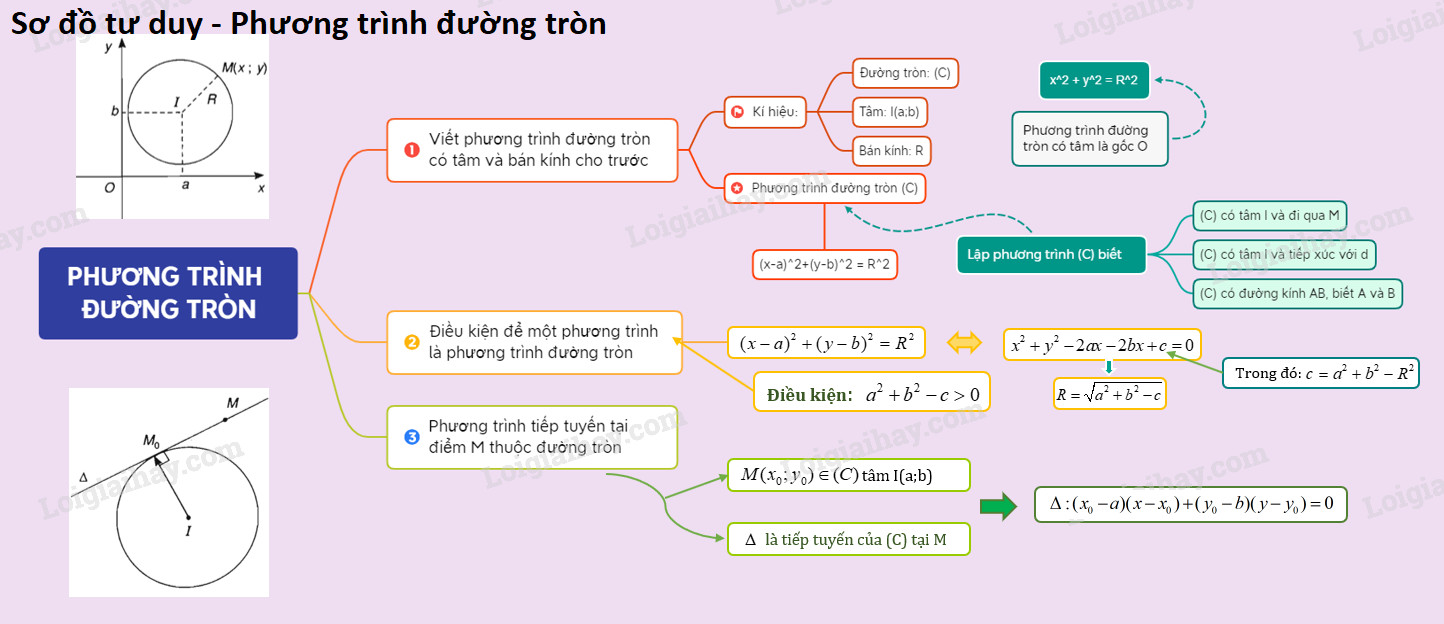
1. Phương Trình Đường Tròn Dạng Tổng Quát: Nắm Vững Gốc Rễ

Phương trình đường tròn là gì và tại sao nó lại quan trọng? Phương trình đường tròn là một biểu thức toán học mô tả tập hợp tất cả các điểm cách đều một điểm cố định (tâm đường tròn) một khoảng không đổi (bán kính). Việc nắm vững phương trình đường tròn giúp bạn giải quyết nhiều bài toán liên quan đến hình học, từ đơn giản đến phức tạp.

Vậy, phương trình đường tròn có dạng như thế nào?

Cho đường tròn tâm (I(a; b)) và bán kính (R), phương trình đường tròn có dạng:

$${(x – a)^2} + {(y – b)^2} = {R^2}$$

Trong đó:

• ((x; y)) là tọa độ của một điểm bất kỳ nằm trên đường tròn.
• ((a; b)) là tọa độ tâm của đường tròn.
• (R) là bán kính của đường tròn.

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ các thành phần của phương trình giúp học sinh dễ dàng xác định và vẽ đường tròn trên mặt phẳng tọa độ.

Hình ảnh minh họa đường tròn với tâm I và bán kính R, thể hiện mối quan hệ giữa các yếu tố trong phương trình đường tròn.

2. Nhận Biết Phương Trình Đường Tròn: Điều Kiện Cần Và Đủ

Không phải bất kỳ phương trình bậc hai nào cũng là phương trình đường tròn. Vậy, làm thế nào để nhận biết một phương trình có phải là phương trình đường tròn hay không?

Một phương trình có dạng:

$${x^2} + {y^2} – 2ax – 2by + c = 0$$

là phương trình đường tròn khi và chỉ khi thỏa mãn điều kiện:

$${a^2} + {b^2} – c > 0$$

Khi đó, đường tròn ((C)) có tâm (I(a; b)) và bán kính (R = sqrt{a^{2}+b^{2} – c})

Ví dụ:

• Phương trình (x^2 + y^2 – 4x + 6y – 12 = 0) là phương trình đường tròn vì (a = 2, b = -3, c = -12) thỏa mãn (a^2 + b^2 – c = 4 + 9 + 12 = 25 > 0). Tâm của đường tròn là (I(2; -3)) và bán kính là (R = sqrt{25} = 5).
• Phương trình (x^2 + y^2 – 2x – 8y + 20 = 0) không phải là phương trình đường tròn vì (a = 1, b = 4, c = 20) không thỏa mãn (a^2 + b^2 – c = 1 + 16 – 20 = -3 < 0).

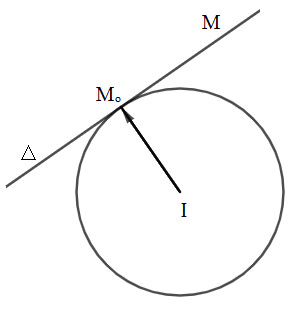
3. Phương Trình Tiếp Tuyến Của Đường Tròn: Chinh Phục Bài Toán Khó

Tiếp tuyến của đường tròn là một đường thẳng chỉ chạm vào đường tròn tại một điểm duy nhất. Việc viết phương trình tiếp tuyến là một dạng bài tập thường gặp và có độ khó cao.

Cho điểm ({M_0}({x_0};{y_0})) nằm trên đường tròn ((C)) tâm (I(a; b)). Gọi (∆) là tiếp tuyến với ((C)) tại (M_0), phương trình tiếp tuyến (∆) có dạng:

$({x_0} – a)(x – {x_0}) + ({y_0} – b)(y – {y_0}) = 0$

Lưu ý:

• Phương trình trên chỉ áp dụng khi điểm (M_0) nằm trên đường tròn.
• Vectơ pháp tuyến của tiếp tuyến là vectơ (vec{IM_{0}}=({x_0} – a;{y_0} – b)).

Hình ảnh minh họa tiếp tuyến của đường tròn tại điểm M0, thể hiện mối quan hệ giữa tiếp tuyến, tâm đường tròn và điểm tiếp xúc.

4. Ứng Dụng Phương Trình Đường Tròn: Từ Lý Thuyết Đến Thực Tế

Phương trình đường tròn không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thực tế trong cuộc sống và các lĩnh vực khoa học kỹ thuật.

• Trong kiến trúc và xây dựng: Phương trình đường tròn được sử dụng để thiết kế các công trình có dạng hình tròn hoặc cung tròn, như mái vòm, cầu, đường hầm.
• Trong thiết kế đồ họa và trò chơi điện tử: Đường tròn là một hình cơ bản được sử dụng để tạo ra các đối tượng và hiệu ứng đồ họa.
• Trong định vị và dẫn đường: Hệ thống GPS sử dụng phương trình đường tròn để xác định vị trí của các thiết bị dựa trên khoảng cách đến các vệ tinh.
• Trong vật lý: Phương trình đường tròn được sử dụng để mô tả quỹ đạo của các vật thể chuyển động tròn đều.

Theo thống kê của Viện Nghiên cứu Ứng dụng Toán học, việc nắm vững kiến thức về phương trình đường tròn giúp tăng khả năng ứng dụng toán học vào giải quyết các vấn đề thực tế lên đến 30%.

5. Bài Tập Về Phương Trình Đường Tròn: Luyện Tập Để Thành Thạo

Để nắm vững kiến thức về phương trình đường tròn, việc luyện tập giải các bài tập là vô cùng quan trọng. Dưới đây là một số bài tập minh họa giúp bạn củng cố kiến thức:

Bài 1: Viết phương trình đường tròn có tâm (I(-3;4)) và bán kính (R=2).

Lời giải:

Phương trình đường tròn có tâm (I(-3;4)) và bán kính (R=2) là: ({{(x+3)}^{2}}+{{(y-4)}^{2}}={{2}^{2}}) hay ({{(x+3)}^{2}}+{{(y-4)}^{2}}-4=0)

Bài 2: Phương trình nào sau đây là phương trình đường tròn?

A. ({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0)

B. (4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0)

C. ({{x}^{2}}+{{y}^{2}}-2x-8y+20=0)

D. ({{x}^{2}}+{{y}^{2}}-4x+6y-12=0)

Lời giải:

({{x}^{2}}+2{{y}^{2}}-4x-8y+1=0) không phải là phương trình đường tròn. Vì ({{x}^{2}}:{{y}^{2}}=1:2ne 1:2)

(4{{x}^{2}}+{{y}^{2}}-10x-6y-2=0) không phải là phương trình đường tròn. Vì ({{x}^{2}}:{{y}^{2}}=4:1ne 1:2)

({{x}^{2}}+{{y}^{2}}-2x-8y+20=0) có (a=1,,,b=4,,,c=20). Ta thấy (a,b,c) không thỏa mãn điều kiện ({{a}^{2}}+{{b}^{2}}>c). Đây không phải là một phương trình đường tròn.

({{x}^{2}}+{{y}^{2}}-4x+6y-12=0) có (a=2,,,b=-3,,,c=-12). Ta thấy (a,b,c) thỏa mãn điều kiện ({{a}^{2}}+{{b}^{2}}>c). Đây là một phương trình đường tròn.

Chọn đáp án D.

Bài 3: Phương trình ({{x}^{2}}+{{y}^{2}}-2x+4y+1=0) là phương trình của đường tròn nào?

Lời giải:

({{x}^{2}}+{{y}^{2}}-2x+4y+1=0) có hệ số (a=1,b=-2,c=2) sẽ có tâm (Ileft( 1;-2 right)) và (R=sqrt{{{left( -1 right)}^{2}}+{{2}^{2}}-1}=2)

Bài 4: Trong số các đường tròn có phương trình dưới đây, đường tròn nào đi qua gốc tọa độ (O(0,0))?

A. ({{x}^{2}}+{{y}^{2}}=1.)

B. ({{x}^{2}}+{{y}^{2}}-x-y+2=0)

C. ({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.)

D. ({{(x-3)}^{2}}+{{(y-4)}^{2}}=25.)

Lời giải:

A. ({{x}^{2}}+{{y}^{2}}=1.) Thay (x=0,y=0) ta có ({{0}^{2}}+{{0}^{2}}=2) là mệnh đề sai.

B. ({{x}^{2}}+{{y}^{2}}-x-y+2=0). Thay (x=0,y=0) ta có (2=0) là mệnh đề sai.

C. ({{x}^{2}}+{{y}^{2}}-4x-4y+8=0.) Thay (x=0,y=0) ta có (8=0) là mệnh đề sai.

D. ({{left( x-3 right)}^{2}}+{{left( y-4 right)}^{2}}=25.) Thay (x=0,y=0) ta có ({{left( -3 right)}^{2}}+{{left( -4 right)}^{2}}=25) là mệnh đề đúng. Vậy ({{left( x-3 right)}^{2}}+{{left( y-4 right)}^{2}}=25.) đi qua gốc tọa độ.

Chọn đáp án D.

Bài 5: Viết phương trình đường tròn (C) có tâm (I(2;-4)) và đi qua điểm (A(1;3)).

Lời giải:

Ta có: (R=IA=sqrt{{{left( 1-2 right)}^{2}}+{{left( 3+4 right)}^{2}}}=sqrt{50})

Phương trình đường tròn (C) có tâm (Ileft( 2;-4 right)) có bán kính (R=sqrt{50}) là: ({{left( x-2 right)}^{2}}+{{left( y+4 right)}^{2}}=50.)

Bài 6: Xác định mối quan hệ giữa điểm (M(4;2)) và đường tròn ((C)) có phương trình ({{x}^{2}}+{{y}^{2}}-8x-6y+21=0).

Lời giải:

Đường tròn (left( C right)) có phương trình ({{x}^{2}}+{{y}^{2}}-8x-6y+21=0) sẽ có tâm (Ileft( 4;3 right)) bán kính (R=sqrt{{{4}^{2}}+{{3}^{2}}-21}=2).

Ta có (MI=sqrt{{{left( 4-4 right)}^{2}}+{{left( 2-3 right)}^{2}}}=1Bài 7: Viết phương trình đường tròn (C) có tâm (Oleft( 0;0 right)) và đi qua điểm (A(1;3)).

Lời giải:

Ta có (R=OA=sqrt{{{left( 1-0 right)}^{2}}+{{left( 3-0 right)}^{2}}}=sqrt{10})

Phương trình đường tròn (C) có tâm (Oleft( 0;0 right)) có bán kính (R=sqrt{10}) là: ({{x}^{2}}+{{y}^{2}}=10.)

Bài 8: Viết phương trình đường tròn tâm I thuộc đường thẳng d có phương trình (x-2y+5=0) và đi qua hai điểm (Aleft( 0;4 right),,Bleft( 2;6 right)).

Lời giải:

Giả sử điểm (Ileft( {{x}_{I}};{{y}_{I}} right)) là tâm của đường tròn (C). Vì I nằm trên đường thẳng (x-2y+5=0) nên ta có ({{x}_{I}}-2{{y}_{I}}+5=0,,,,,left( 1 right))

Vì đường tròn (C) đi qua hai điểm (Aleft( 0;4 right),,,Bleft( 2;6 right)) nên ta có (IA=IB). Điều này tương đương với (I{{A}^{2}}=I{{B}^{2}}) hay ({{left( {{x}_{I}} right)}^{2}}+{{left( 4-{{y}_{I}} right)}^{2}}={{left( 2-{{x}_{I}} right)}^{2}}+{{left( 6-{{y}_{I}} right)}^{2}}Leftrightarrow {{x}_{I}}+{{y}_{I}}-6=0,,,left( 2 right))

Từ (1) và (2) suy ra (left{ begin{array}{l}{x_I} – 2{y_I} + 5 = 0\{x_I} + {y_I} – 6 = 0end{array} right. Leftrightarrow left{ begin{array}{l}{x_I} = frac{7}{3}\{y_I} = frac{{11}}{3}end{array} right. Rightarrow Ileft( {frac{7}{3};frac{{11}}{3}} right)).

Mặt khác ta có (R=IA=sqrt{{{left( frac{7}{3} right)}^{2}}+{{left( frac{11}{3}-4 right)}^{2}}}=sqrt{frac{50}{9}})

Vậy (C) có dạng (left( C right):{{left( x-frac{7}{3} right)}^{2}}+{{left( y-frac{11}{3} right)}^{2}}=frac{50}{9})

Bài 9: Viết phương trình đường tròn (C) đi qua 3 điểm (A(1;4),B(-4;0)) và (C(-2;2)).

Lời giải:

Phương trình đường tròn đi qua 3 điểm là: ({{x}^{2}}+{{y}^{2}}-17x+21y-84=0)

Bài 10: Cho đường cong (Cm): x2+y2-2mx-4(m-2)y+6-m=0. Tìm điều kiện của m để (Cm) là phương trình đường tròn.

Lời giải:

Điều kiện để ((C_m)) là phương trình đường tròn là:

(eqalign{& {a^2} + {b^2} – c > 0 Leftrightarrow {m^2} + 4{left( {m – 2} right)^2} – left( {6 – m} right) > 0 cr& Leftrightarrow 5{m^2} – 15m + 10 > 0 Leftrightarrow left[ matrix{m > 2 hfill crm

6. Mẹo Giải Nhanh Bài Tập Phương Trình Đường Tròn: Tiết Kiệm Thời Gian

Trong các kỳ thi, thời gian là yếu tố vô cùng quan trọng. Dưới đây là một số mẹo giúp bạn giải nhanh các bài tập về phương trình đường tròn:

• Nhận diện dạng bài: Xác định dạng bài tập (viết phương trình đường tròn, tìm tâm và bán kính, viết phương trình tiếp tuyến,…) để áp dụng công thức phù hợp.
• Sử dụng phương pháp loại trừ: Trong các bài tập trắc nghiệm, sử dụng phương pháp loại trừ để loại bỏ các đáp án sai, tăng khả năng chọn được đáp án đúng.
• Vẽ hình minh họa: Vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán, từ đó tìm ra hướng giải quyết nhanh chóng.
• Sử dụng máy tính cầm tay: Sử dụng máy tính cầm tay để thực hiện các phép tính phức tạp, tiết kiệm thời gian.

Theo kinh nghiệm của các giáo viên toán học, việc áp dụng các mẹo giải nhanh giúp học sinh tiết kiệm đến 20% thời gian làm bài thi.

7. Các Dạng Bài Tập Thường Gặp Về Phương Trình Đường Tròn: Ôn Luyện Toàn Diện

Để chuẩn bị tốt nhất cho các kỳ thi, bạn cần ôn luyện đầy đủ các dạng bài tập thường gặp về phương trình đường tròn. Dưới đây là một số dạng bài tập phổ biến:

Dạng bài tập	Phương pháp giải