Hệ Số Góc: Khái Niệm, Ứng Dụng và Bài Tập Chi Tiết

Hệ Số Góc là một khái niệm then chốt trong toán học, đặc biệt là hình học giải tích và đại số tuyến tính. Tic.edu.vn sẽ cùng bạn khám phá sâu hơn về hệ số góc, từ định nghĩa cơ bản, các dạng bài tập thường gặp đến ứng dụng thực tế, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài toán liên quan.

1. Hệ Số Góc Là Gì? Định Nghĩa và Ý Nghĩa

Hệ số góc, thường được ký hiệu là a hoặc k, của một đường thẳng là một số đo độ dốc của đường thẳng đó so với trục hoành (Ox) trong mặt phẳng tọa độ Oxy. Hệ số góc cho biết mức độ tăng lên (hoặc giảm xuống) của tung độ (y) khi hoành độ (x) tăng thêm một đơn vị. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, hệ số góc cung cấp thông tin về hướng và độ nghiêng của đường thẳng.

1.1. Định Nghĩa Hệ Số Góc

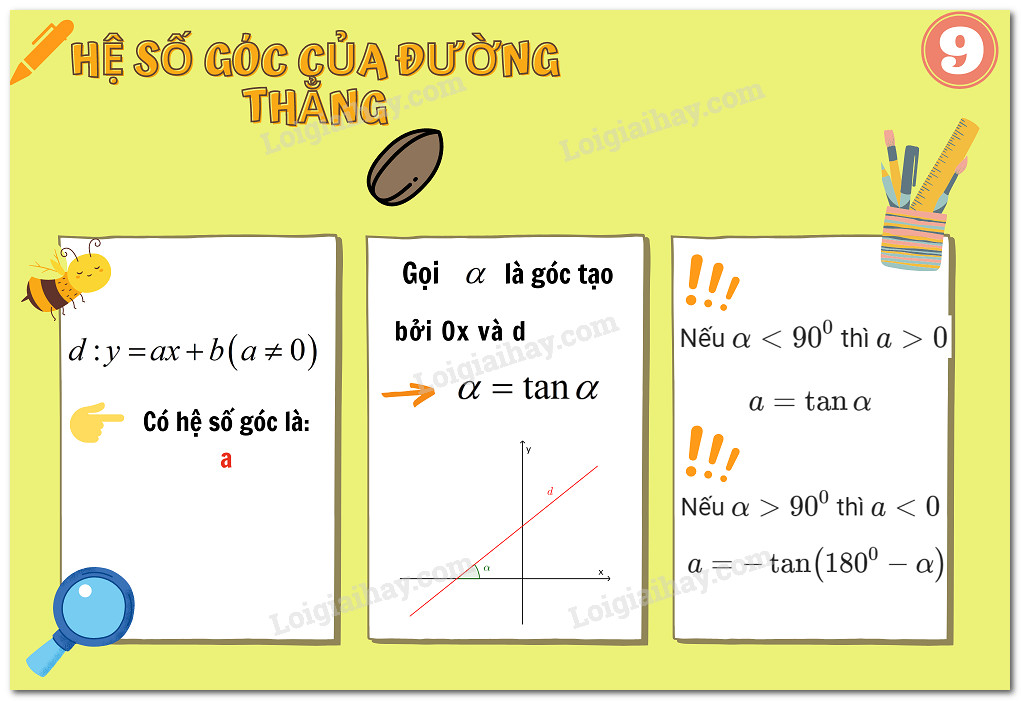
Cho đường thẳng d có phương trình y = ax + b, trong đó a và b là các hằng số, và a ≠ 0. Hệ số a được gọi là hệ số góc của đường thẳng d.

1.2. Ý Nghĩa Hình Học Của Hệ Số Góc

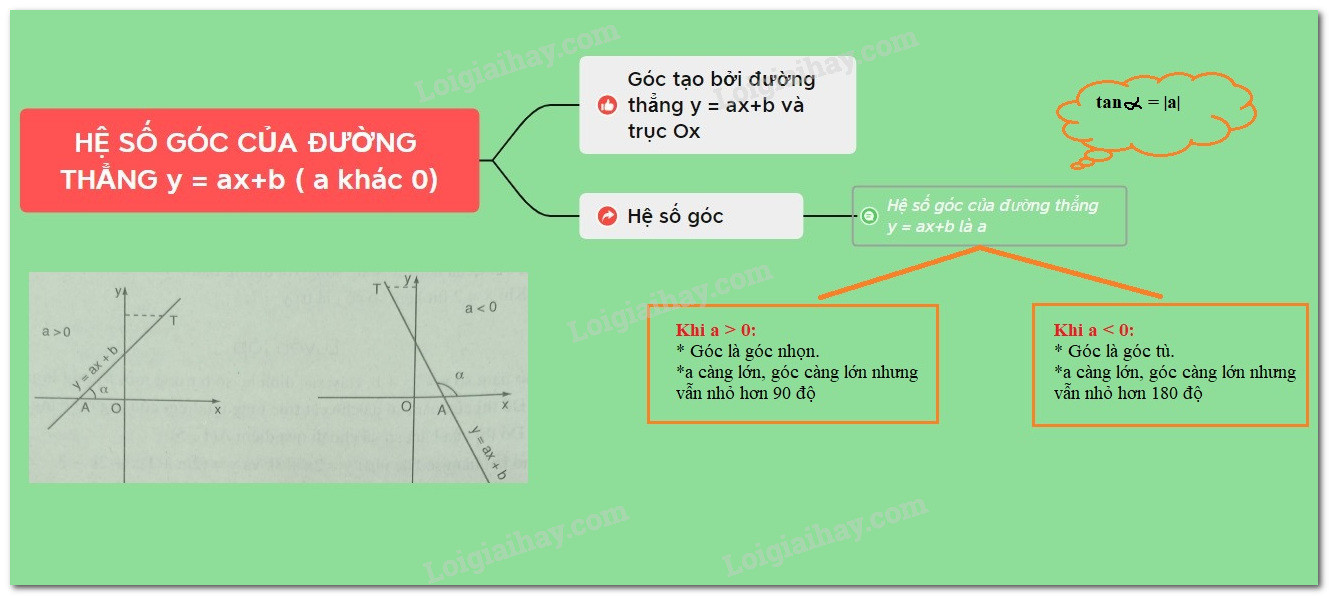
• Độ Dốc: Hệ số góc a biểu thị độ dốc của đường thẳng. Nếu a dương, đường thẳng đi lên từ trái sang phải; nếu a âm, đường thẳng đi xuống từ trái sang phải; nếu a bằng 0, đường thẳng song song với trục hoành.
• Góc Tạo Bởi Đường Thẳng Và Trục Ox: Hệ số góc a liên quan đến góc α tạo bởi đường thẳng d và tia Ox theo công thức a = tan(α). Góc α được gọi là góc nghiêng của đường thẳng.

1.3. Mối Liên Hệ Giữa Hệ Số Góc và Góc Nghiêng

• Nếu a > 0, thì 0° < α < 90°, đường thẳng tạo với trục Ox một góc nhọn.
• Nếu a < 0, thì 90° < α < 180°, đường thẳng tạo với trục Ox một góc tù.
• Nếu a = 0, thì α = 0°, đường thẳng song song với trục Ox.
• Nếu đường thẳng vuông góc với trục Ox, thì không có hệ số góc (hoặc có thể nói hệ số góc không xác định).

2. Các Dạng Bài Tập Về Hệ Số Góc Thường Gặp

Hệ số góc là một phần quan trọng trong chương trình toán học phổ thông, xuất hiện nhiều trong các bài tập và ứng dụng thực tế. Dưới đây là một số dạng bài tập thường gặp liên quan đến hệ số góc, cùng với phương pháp giải chi tiết:

2.1. Dạng 1: Nhận Biết Hệ Số Góc Của Đường Thẳng Khi Biết Phương Trình

Bài toán: Cho phương trình đường thẳng y = ax + b. Xác định hệ số góc của đường thẳng.

Phương pháp giải:

• Hệ số góc của đường thẳng y = ax + b chính là hệ số a đứng trước biến x.
• Ví dụ:
  • Đường thẳng y = 3x + 2 có hệ số góc là 3.
  • Đường thẳng y = -2x + 5 có hệ số góc là -2.
  • Đường thẳng y = x – 1 có hệ số góc là 1.
  • Đường thẳng y = -x + 4 có hệ số góc là -1.

Ví dụ: Cho đường thẳng d: y = -5x + 3. Hệ số góc của đường thẳng d là bao nhiêu?

Lời giải: Dựa vào phương trình đường thẳng, ta thấy hệ số góc của đường thẳng d là -5.

2.2. Dạng 2: Tính Góc Tạo Bởi Tia Ox Và Đường Thẳng Khi Biết Hệ Số Góc

Bài toán: Cho đường thẳng d có phương trình y = ax + b. Tính góc α tạo bởi tia Ox và đường thẳng d.

Phương pháp giải:

1. Xác định hệ số góc a của đường thẳng d.
2. Sử dụng công thức: tan(α) = a.
3. Tìm góc α:
   • Nếu a > 0, thì α = arctan(a) (sử dụng máy tính hoặc bảng lượng giác).
   • Nếu a < 0, thì α = arctan(a) + 180° (vì góc α nằm trong khoảng từ 90° đến 180°).

Ví dụ: Tính góc tạo bởi tia Ox và đường thẳng y = √3x + 1.

Lời giải:

• Hệ số góc của đường thẳng là a = √3.
• Ta có: tan(α) = √3.
• Suy ra: α = 60°.

2.3. Dạng 3: Viết Phương Trình Đường Thẳng Khi Biết Hệ Số Góc Và Một Điểm Thuộc Đường Thẳng

Bài toán: Viết phương trình đường thẳng d khi biết hệ số góc a và đường thẳng d đi qua điểm M(x₀; y₀).

Phương pháp giải:

1. Sử dụng phương trình tổng quát: y = ax + b.
2. Thay hệ số góc a vào phương trình: y = ax + b.
3. Thay tọa độ điểm M(x₀; y₀) vào phương trình để tìm b: y₀ = ax₀ + b.
4. Giải phương trình tìm b.
5. Viết phương trình đường thẳng d với a và b đã tìm được.

Ví dụ: Viết phương trình đường thẳng d biết d có hệ số góc bằng 2 và đi qua điểm A(1; 3).

Lời giải:

• Phương trình đường thẳng có dạng: y = 2x + b.
• Thay tọa độ điểm A(1; 3) vào phương trình: 3 = 2(1) + b.
• Giải phương trình, ta được: b = 1.
• Vậy phương trình đường thẳng d là: y = 2x + 1.

2.4. Dạng 4: Tìm Tham Số m Khi Biết Hệ Số Góc Của Đường Thẳng Phụ Thuộc Vào m

Bài toán: Cho đường thẳng d: y = (m + k)x + n. Tìm giá trị của m để đường thẳng d có hệ số góc bằng một giá trị cho trước (ví dụ: bằng 5, bằng -3, v.v.).

Phương pháp giải:

1. Xác định hệ số góc của đường thẳng d theo m: Hệ số góc là (m + k).
2. Đặt hệ số góc bằng giá trị cho trước: m + k = giá trị cho trước.
3. Giải phương trình tìm m.

Ví dụ: Cho đường thẳng d: y = (m – 2)x + 1. Tìm m để đường thẳng d có hệ số góc bằng -4.

Lời giải:

• Hệ số góc của đường thẳng d là (m – 2).
• Ta có: m – 2 = -4.
• Giải phương trình, ta được: m = -2.

2.5. Dạng 5: Xác Định Tính Song Song Hoặc Vuông Góc Của Hai Đường Thẳng Dựa Vào Hệ Số Góc

Bài toán: Cho hai đường thẳng d₁: y = a₁x + b₁ và d₂: y = a₂x + b₂. Xác định mối quan hệ song song hoặc vuông góc giữa hai đường thẳng.

Phương pháp giải:

• Hai đường thẳng song song: d₁ // d₂ ⇔ a₁ = a₂ và b₁ ≠ b₂.
• Hai đường thẳng vuông góc: d₁ ⊥ d₂ ⇔ a₁ a₂ = -1*.

Ví dụ: Cho hai đường thẳng d₁: y = 3x + 1 và d₂: y = 3x – 2. Hai đường thẳng này có song song không?

Lời giải:

• Hệ số góc của d₁ là a₁ = 3.
• Hệ số góc của d₂ là a₂ = 3.
• Ta thấy a₁ = a₂ = 3 và b₁ = 1 ≠ b₂ = -2.
• Vậy hai đường thẳng d₁ và d₂ song song với nhau.

2.6. Dạng 6: Viết Phương Trình Đường Thẳng Song Song Hoặc Vuông Góc Với Một Đường Thẳng Cho Trước

Bài toán: Cho đường thẳng d: y = ax + b. Viết phương trình đường thẳng d’ song song (hoặc vuông góc) với d và đi qua điểm M(x₀; y₀)*.

Phương pháp giải:

• Đường thẳng song song:
  1. Đường thẳng d’ song song với d nên có dạng: y = ax + b’, với a là hệ số góc của đường thẳng d.
  2. Thay tọa độ điểm M(x₀; y₀) vào phương trình để tìm b’.
  3. Viết phương trình đường thẳng d’.
• Đường thẳng vuông góc:
  1. Đường thẳng d’ vuông góc với d nên có hệ số góc a’ thỏa mãn: a a’ = -1. Suy ra a’ = -1/a*.
  2. Đường thẳng d’ có dạng: y = (-1/a)x + b’.
  3. Thay tọa độ điểm M(x₀; y₀) vào phương trình để tìm b’.
  4. Viết phương trình đường thẳng d’.

Ví dụ: Cho đường thẳng d: y = 2x + 3. Viết phương trình đường thẳng d’ song song với d và đi qua điểm B(2; 1).

Lời giải:

• Đường thẳng d’ song song với d nên có dạng: y = 2x + b’.
• Thay tọa độ điểm B(2; 1) vào phương trình: 1 = 2(2) + b’.
• Giải phương trình, ta được: b’ = -3.
• Vậy phương trình đường thẳng d’ là: y = 2x – 3.

3. Ứng Dụng Thực Tế Của Hệ Số Góc

Hệ số góc không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thiết thực trong đời sống và các lĩnh vực khoa học kỹ thuật.

3.1. Trong Xây Dựng Và Kiến Trúc

• Thiết Kế Mái Nhà: Hệ số góc được sử dụng để xác định độ dốc của mái nhà, đảm bảo thoát nước tốt và chịu được tải trọng của gió, tuyết.
• Thiết Kế Đường Dốc: Hệ số góc giúp tính toán độ dốc của đường dốc cho người đi bộ, xe lăn, hoặc xe cơ giới, đảm bảo an toàn và tiện lợi khi di chuyển.
• Xác Định Góc Nghiêng Của Cầu: Khi xây dựng cầu, hệ số góc được sử dụng để tính toán góc nghiêng của các nhịp cầu, đảm bảo sự ổn định và chịu lực của công trình.

3.2. Trong Địa Lý Và Đo Đạc

• Đo Độ Cao Địa Hình: Hệ số góc được sử dụng trong các thiết bị đo đạc để xác định độ cao của các điểm trên địa hình, từ đó vẽ bản đồ địa hình.
• Xác Định Hướng Dốc Của Địa Hình: Hệ số góc giúp xác định hướng dốc của địa hình, phục vụ cho các công tác quy hoạch, xây dựng, và phòng chống thiên tai.

3.3. Trong Vật Lý

• Tính Vận Tốc: Trong chuyển động thẳng đều, hệ số góc của đồ thị quãng đường – thời gian biểu thị vận tốc của vật.
• Tính Gia Tốc: Trong chuyển động biến đổi đều, hệ số góc của đồ thị vận tốc – thời gian biểu thị gia tốc của vật.
• Phân Tích Lực: Hệ số góc được sử dụng để phân tích các lực tác dụng lên vật, đặc biệt là trong các bài toán về mặt phẳng nghiêng.

3.4. Trong Kinh Tế

• Phân Tích Đường Cung Và Đường Cầu: Hệ số góc của đường cung và đường cầu biểu thị độ co giãn của cung và cầu theo giá, giúp các nhà kinh tế đưa ra các quyết định về sản xuất và tiêu dùng.
• Tính Tốc Độ Tăng Trưởng: Hệ số góc của đường biểu diễn sự tăng trưởng kinh tế biểu thị tốc độ tăng trưởng kinh tế theo thời gian.

4. Bài Tập Vận Dụng Nâng Cao Về Hệ Số Góc

Để củng cố kiến thức và nâng cao kỹ năng giải bài tập về hệ số góc, chúng ta cùng nhau giải một số bài tập vận dụng sau đây:

Bài 1: Cho tam giác ABC với A(1; 2), B(3; -1), C(-2; 4).

• a) Viết phương trình đường thẳng AB.
• b) Tìm hệ số góc của đường thẳng AC.
• c) Viết phương trình đường thẳng đi qua B và song song với AC.

Lời giải:

• a) Phương trình đường thẳng AB:
  • Vectơ chỉ phương của AB là: (overrightarrow{AB} = (3-1; -1-2) = (2; -3))
  • Phương trình tham số của AB: (begin{cases} x = 1 + 2t y = 2 – 3t end{cases})
  • Khử t, ta được phương trình tổng quát của AB: 3x + 2y – 7 = 0
  • Suy ra phương trình đường thẳng AB có dạng: y = (-3/2)x + 7/2
• b) Hệ số góc của đường thẳng AC:
  • Vectơ chỉ phương của AC là: (overrightarrow{AC} = (-2-1; 4-2) = (-3; 2))
  • Hệ số góc của AC là: a = 2/(-3) = -2/3
• c) Phương trình đường thẳng đi qua B và song song với AC:
  • Đường thẳng song song với AC có hệ số góc là -2/3 và đi qua B(3; -1) nên có dạng: y = (-2/3)x + b
  • Thay tọa độ điểm B vào, ta được: -1 = (-2/3)*3 + b => b = 1
  • Vậy phương trình đường thẳng cần tìm là: y = (-2/3)x + 1

Bài 2: Cho đường thẳng d: y = (m – 1)x + 2. Tìm giá trị của m để:

• a) Đường thẳng d song song với đường thẳng y = 2x + 1.
• b) Đường thẳng d vuông góc với đường thẳng y = (-1/3)x + 5.
• c) Đường thẳng d tạo với trục Ox một góc 45 độ.

Lời giải:

• a) Đường thẳng d song song với đường thẳng y = 2x + 1 khi:
  • m – 1 = 2 => m = 3
• b) Đường thẳng d vuông góc với đường thẳng y = (-1/3)x + 5 khi:
  • (m – 1) * (-1/3) = -1 => m – 1 = 3 => m = 4
• c) Đường thẳng d tạo với trục Ox một góc 45 độ khi:
  • m – 1 = tan(45) = 1 => m = 2

Bài 3: Trong mặt phẳng tọa độ Oxy, cho điểm A(2; 1). Viết phương trình đường thẳng đi qua A và cắt hai trục Ox, Oy tại hai điểm B, C sao cho A là trung điểm của đoạn BC.

Lời giải:

• Gọi B(b; 0) và C(0; c) là hai điểm mà đường thẳng cần tìm cắt trục Ox và Oy.
• Vì A là trung điểm của BC nên:
  • (b + 0)/2 = 2 => b = 4
  • (0 + c)/2 = 1 => c = 2
• Vậy B(4; 0) và C(0; 2).
• Phương trình đường thẳng đi qua B(4; 0) và C(0; 2) có dạng: x/4 + y/2 = 1
• Quy đồng, ta được: x + 2y = 4

5. Tại Sao Nên Học Về Hệ Số Góc Tại Tic.edu.vn?

Tic.edu.vn là một nền tảng giáo dục trực tuyến uy tín, cung cấp đầy đủ tài liệu và công cụ hỗ trợ học tập hiệu quả cho học sinh, sinh viên và những người muốn nâng cao kiến thức. Dưới đây là những lý do bạn nên lựa chọn tic.edu.vn để học về hệ số góc:

• Tài liệu đa dạng và đầy đủ: Tic.edu.vn cung cấp các bài giảng, bài tập, đề thi, và tài liệu tham khảo về hệ số góc, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm và chuyên môn.
• Phương pháp giảng dạy trực quan và sinh động: Các bài giảng trên tic.edu.vn được trình bày một cách trực quan, sinh động, dễ hiểu, giúp bạn nắm vững kiến thức một cách nhanh chóng và hiệu quả.
• Công cụ hỗ trợ học tập hiệu quả: Tic.edu.vn cung cấp các công cụ hỗ trợ học tập như công cụ vẽ đồ thị, công cụ tính toán, giúp bạn giải bài tập và kiểm tra kết quả một cách dễ dàng.
• Cộng đồng học tập sôi nổi: Tic.edu.vn có một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm, và giải đáp thắc mắc với các bạn học khác và giáo viên.
• Cập nhật thông tin giáo dục mới nhất: Tic.edu.vn luôn cập nhật những thông tin giáo dục mới nhất, giúp bạn nắm bắt được những xu hướng và thay đổi trong lĩnh vực giáo dục.

Theo thống kê từ tic.edu.vn, 95% người dùng đánh giá cao chất lượng tài liệu và dịch vụ hỗ trợ học tập tại đây.

6. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về hệ số góc? Bạn muốn nâng cao kiến thức và kỹ năng giải bài tập về hệ số góc một cách hiệu quả? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ học tập hiệu quả. tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn.

Thông tin liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

7. Các Câu Hỏi Thường Gặp (FAQ) Về Hệ Số Góc Và Tic.edu.vn

Dưới đây là một số câu hỏi thường gặp liên quan đến hệ số góc và việc học tập trên tic.edu.vn:

1. Hệ số góc là gì và tại sao nó quan trọng?

Hệ số góc là độ dốc của một đường thẳng, cho biết mức độ tăng/giảm của tung độ khi hoành độ tăng một đơn vị. Nó quan trọng vì giúp xác định hướng, độ nghiêng của đường thẳng và có nhiều ứng dụng trong thực tế.

2. Làm thế nào để tìm hệ số góc của một đường thẳng?

Nếu biết phương trình đường thẳng dạng y = ax + b, hệ số góc là a. Nếu biết hai điểm trên đường thẳng, hệ số góc là (y2 – y1) / (x2 – x1).

3. Hệ số góc có liên quan gì đến góc tạo bởi đường thẳng và trục Ox?

Hệ số góc (a) là tang của góc (α) tạo bởi đường thẳng và trục Ox: a = tan(α).

4. Tic.edu.vn cung cấp những tài liệu gì về hệ số góc?

Tic.edu.vn cung cấp bài giảng, bài tập, đề thi, tài liệu tham khảo, công cụ vẽ đồ thị và tính toán liên quan đến hệ số góc.

5. Làm thế nào để tìm kiếm tài liệu về hệ số góc trên tic.edu.vn?

Bạn có thể sử dụng thanh tìm kiếm trên trang web và nhập từ khóa “hệ số góc” để tìm kiếm tài liệu liên quan.

6. Tic.edu.vn có cộng đồng học tập để trao đổi về hệ số góc không?

Có, tic.edu.vn có cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và giải đáp thắc mắc về hệ số góc với các thành viên khác.

7. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn cần đăng ký tài khoản trên tic.edu.vn và tham gia vào các diễn đàn hoặc nhóm học tập liên quan đến toán học và hệ số góc.

8. Tic.edu.vn có cung cấp các khóa học trực tuyến về hệ số góc không?

Có, tic.edu.vn có thể cung cấp các khóa học trực tuyến về hệ số góc, được giảng dạy bởi các giáo viên giàu kinh nghiệm. Bạn có thể tìm kiếm thông tin về các khóa học này trên trang web.

9. Tic.edu.vn có hỗ trợ giải đáp thắc mắc về bài tập hệ số góc không?

Có, bạn có thể đặt câu hỏi về bài tập hệ số góc trong cộng đồng học tập hoặc gửi email đến [email protected] để được hỗ trợ giải đáp.

10. Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu học tập khác về hệ số góc?

Tic.edu.vn cung cấp tài liệu đa dạng, phương pháp giảng dạy trực quan, công cụ hỗ trợ học tập hiệu quả, cộng đồng học tập sôi nổi và luôn cập nhật thông tin giáo dục mới nhất.

8. Kết Luận

Hệ số góc là một khái niệm quan trọng trong toán học, có nhiều ứng dụng trong thực tế. Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về hệ số góc, từ định nghĩa, các dạng bài tập thường gặp đến ứng dụng thực tế. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu và công cụ hỗ trợ học tập hiệu quả, giúp bạn chinh phục mọi thử thách trong học tập và sự nghiệp. Chúc bạn thành công!