Góc Nhị Diện, một khái niệm then chốt trong hình học không gian, đóng vai trò quan trọng trong việc giải quyết nhiều bài toán và ứng dụng thực tế. Hãy cùng tic.edu.vn khám phá sâu hơn về góc nhị diện, từ định nghĩa cơ bản đến các phương pháp tính toán và ứng dụng thú vị của nó trong đời sống.
Contents
- 2. Góc Nhị Diện Là Gì? Định Nghĩa Chi Tiết Nhất
- 2.1. Định Nghĩa Góc Nhị Diện
- 2.2. Các Yếu Tố Của Góc Nhị Diện
- 2.3. Kí Hiệu Góc Nhị Diện
- 3. Nửa Mặt Phẳng: Thành Phần Quan Trọng Của Góc Nhị Diện
- 3.1. Định Nghĩa Nửa Mặt Phẳng
- 3.2. Mối Liên Hệ Giữa Nửa Mặt Phẳng Và Góc Nhị Diện
- 4. Góc Phẳng Nhị Diện: Đo Lường Độ Lớn Góc Nhị Diện
- 4.1. Định Nghĩa Góc Phẳng Nhị Diện
- 4.2. Cách Xác Định Góc Phẳng Nhị Diện
- 4.3. Tính Chất Quan Trọng Của Góc Phẳng Nhị Diện
- 5. Số Đo Của Góc Nhị Diện: Hiểu Rõ Để Giải Toán Hiệu Quả
- 5.1. Định Nghĩa Số Đo Góc Nhị Diện
- 5.2. Đơn Vị Đo Góc Nhị Diện
- 5.3. Giá Trị Của Góc Nhị Diện
- 6. Các Dạng Bài Tập Về Góc Nhị Diện Thường Gặp
- 6.1. Dạng 1: Xác Định Góc Phẳng Nhị Diện
- 6.2. Dạng 2: Tính Số Đo Góc Nhị Diện
- 6.3. Dạng 3: Ứng Dụng Góc Nhị Diện Trong Các Bài Toán Thực Tế
- 7. Bài Tập Về Góc Nhị Diện: Luyện Tập Để Nắm Vững Kiến Thức
- 8. Ứng Dụng Thực Tế Của Góc Nhị Diện Trong Đời Sống
- 9. Các Công Cụ Hỗ Trợ Học Tập Về Góc Nhị Diện Trên Tic.edu.vn
- 10. Tại Sao Nên Chọn Tic.edu.vn Để Học Về Góc Nhị Diện?
- 11. Các Câu Hỏi Thường Gặp Về Góc Nhị Diện (FAQ)
- 12. Lời Kêu Gọi Hành Động (CTA)
2. Góc Nhị Diện Là Gì? Định Nghĩa Chi Tiết Nhất
Góc nhị diện là một khái niệm hình học không gian dùng để chỉ góc tạo bởi hai nửa mặt phẳng có chung một đường thẳng làm cạnh. Vậy góc nhị diện được định nghĩa như thế nào và nó có những yếu tố nào?
2.1. Định Nghĩa Góc Nhị Diện
Góc nhị diện là hình được tạo bởi hai nửa mặt phẳng có chung bờ. Đường thẳng chung này được gọi là cạnh của góc nhị diện, và mỗi nửa mặt phẳng được gọi là một mặt của góc nhị diện.
Ví dụ, xét góc nhị diện được tạo bởi hai nửa mặt phẳng (P) và (Q) có chung bờ là đường thẳng d, ký hiệu là [P, d, Q]. Đường thẳng d được gọi là cạnh của góc nhị diện, và mỗi nửa mặt phẳng (P) và (Q) được gọi là một mặt của góc nhị diện.
2.2. Các Yếu Tố Của Góc Nhị Diện
- Cạnh: Đường thẳng chung của hai nửa mặt phẳng tạo nên góc nhị diện.
- Mặt: Mỗi nửa mặt phẳng tạo nên góc nhị diện.
- Góc phẳng nhị diện: Góc tạo bởi hai đường thẳng vuông góc với cạnh của góc nhị diện, mỗi đường thẳng nằm trên một mặt của góc nhị diện.
Alt: Hình ảnh minh họa góc nhị diện với các thành phần cơ bản như cạnh và mặt.
2.3. Kí Hiệu Góc Nhị Diện
Góc nhị diện có thể được ký hiệu bằng nhiều cách, ví dụ:
- [P, d, Q]: Trong đó P và Q là hai mặt, d là cạnh.
- [M, d, N]: Trong đó M và N là hai điểm lần lượt thuộc hai mặt P và Q nhưng không thuộc đường thẳng d.
3. Nửa Mặt Phẳng: Thành Phần Quan Trọng Của Góc Nhị Diện
Nửa mặt phẳng là một khái niệm cơ bản trong hình học, đặc biệt quan trọng khi nghiên cứu về góc nhị diện. Vậy nửa mặt phẳng là gì và nó liên quan như thế nào đến góc nhị diện?
3.1. Định Nghĩa Nửa Mặt Phẳng
Một đường thẳng nằm trong mặt phẳng chia mặt phẳng đó thành hai phần, mỗi phần được gọi là một nửa mặt phẳng và đường thẳng đó được gọi là bờ của nửa mặt phẳng này.
3.2. Mối Liên Hệ Giữa Nửa Mặt Phẳng Và Góc Nhị Diện
Góc nhị diện được hình thành từ hai nửa mặt phẳng có chung một đường thẳng làm bờ. Mỗi nửa mặt phẳng này là một mặt của góc nhị diện.
4. Góc Phẳng Nhị Diện: Đo Lường Độ Lớn Góc Nhị Diện
Để đo độ lớn của một góc nhị diện, ta sử dụng khái niệm góc phẳng nhị diện. Vậy góc phẳng nhị diện là gì và nó được xác định như thế nào?
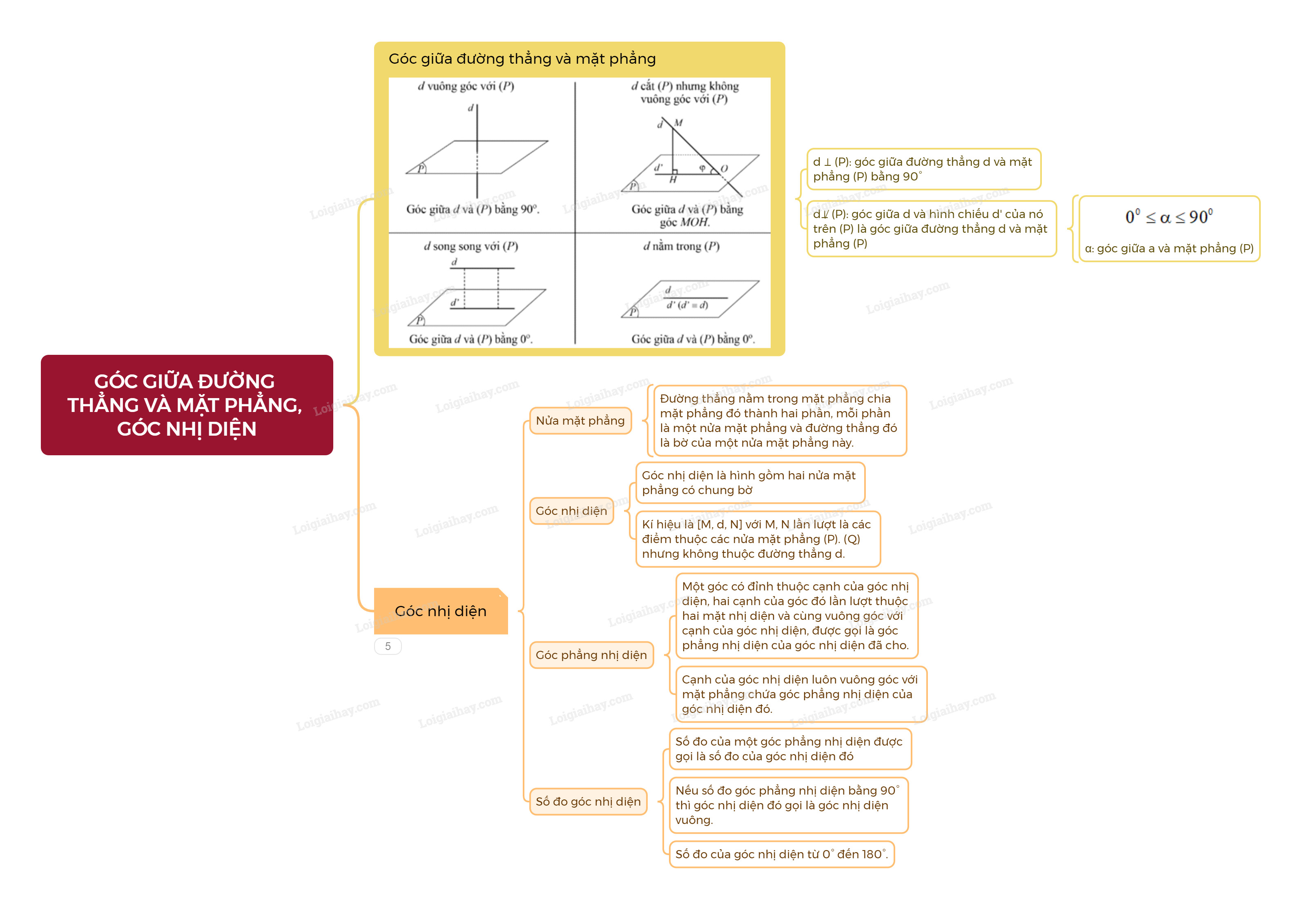
4.1. Định Nghĩa Góc Phẳng Nhị Diện
Trong không gian, cho góc nhị diện. Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.
4.2. Cách Xác Định Góc Phẳng Nhị Diện
Cho góc nhị diện [P, d, Q]. Lấy một điểm O bất kỳ thuộc đường thẳng d (cạnh của góc nhị diện). Từ O, vẽ hai tia Ox và Oy lần lượt nằm trên hai nửa mặt phẳng (P) và (Q) sao cho Ox và Oy cùng vuông góc với d. Khi đó, góc xOy là góc phẳng nhị diện của góc nhị diện [P, d, Q].
Alt: Minh họa góc phẳng nhị diện được tạo thành từ hai tia vuông góc với cạnh của góc nhị diện.
4.3. Tính Chất Quan Trọng Của Góc Phẳng Nhị Diện
Cạnh của góc nhị diện luôn vuông góc với mặt phẳng chứa góc phẳng nhị diện của góc nhị diện đó. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, tính chất này giúp đơn giản hóa việc tính toán và xác định góc nhị diện trong nhiều bài toán hình học không gian.
5. Số Đo Của Góc Nhị Diện: Hiểu Rõ Để Giải Toán Hiệu Quả
Số đo của góc nhị diện là một yếu tố quan trọng để xác định và tính toán các bài toán liên quan. Vậy số đo này được định nghĩa như thế nào?
5.1. Định Nghĩa Số Đo Góc Nhị Diện
Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.
5.2. Đơn Vị Đo Góc Nhị Diện
Số đo của góc nhị diện thường được tính bằng độ (°) hoặc radian.
5.3. Giá Trị Của Góc Nhị Diện
Số đo của góc nhị diện nằm trong khoảng từ 0° đến 180°. Nếu số đo góc phẳng nhị diện bằng 90°, thì góc nhị diện đó được gọi là góc nhị diện vuông.
Alt: Hình ảnh minh họa góc nhị diện vuông với góc phẳng nhị diện bằng 90 độ.
6. Các Dạng Bài Tập Về Góc Nhị Diện Thường Gặp
Để nắm vững kiến thức về góc nhị diện, việc luyện tập các dạng bài tập là vô cùng quan trọng. Dưới đây là một số dạng bài tập thường gặp và cách giải quyết chúng:
6.1. Dạng 1: Xác Định Góc Phẳng Nhị Diện
Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a√2. Xác định góc phẳng nhị diện của góc nhị diện [B, CD, S].
Giải:
- Xác định cạnh của góc nhị diện: Cạnh của góc nhị diện là CD.
- Tìm hai đường thẳng lần lượt nằm trên hai mặt của góc nhị diện và cùng vuông góc với cạnh CD. Trong mặt phẳng (ABCD), kẻ BE vuông góc với CD tại E. Trong mặt phẳng (SCD), kẻ SF vuông góc với CD tại F.
- Chứng minh góc BEF là góc phẳng nhị diện của góc nhị diện [B, CD, S].
- Tính số đo góc BEF.
6.2. Dạng 2: Tính Số Đo Góc Nhị Diện
Bài toán: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Tính số đo của góc nhị diện [A, BC, S].
Giải:
- Xác định góc phẳng nhị diện của góc nhị diện [A, BC, S]. Gọi H là trung điểm của AB. Vì tam giác SAB đều nên SH vuông góc với AB. Do mặt phẳng (SAB) vuông góc với mặt phẳng (ABCD) nên SH vuông góc với mặt phẳng (ABCD). Kẻ HE vuông góc với BC tại E. Khi đó, góc SHE là góc phẳng nhị diện của góc nhị diện [A, BC, S].
- Tính số đo góc SHE. Tính SH và HE, sau đó sử dụng các hàm lượng giác để tính góc SHE.
6.3. Dạng 3: Ứng Dụng Góc Nhị Diện Trong Các Bài Toán Thực Tế
Bài toán: Một mái nhà có hai mặt phẳng tạo với nhau một góc 120°. Người ta cần lợp mái nhà bằng các tấm tôn có chiều rộng 1 mét. Hỏi chiều dài của mỗi tấm tôn cần phải cắt là bao nhiêu để lợp vừa khít một mặt mái nhà?
Giải:
- Xác định góc nhị diện: Góc nhị diện giữa hai mặt mái nhà là 120°.
- Sử dụng kiến thức về hình học để giải bài toán. Chiều dài của mỗi tấm tôn cần phải cắt bằng chiều rộng của mái nhà chia cho sin của nửa góc nhị diện.
7. Bài Tập Về Góc Nhị Diện: Luyện Tập Để Nắm Vững Kiến Thức
Dưới đây là một số bài tập về góc nhị diện để bạn luyện tập và củng cố kiến thức:
Bài 1. Cho tứ diện ABCD có cạnh AB, BC, CD bằng nhau và vuông góc với nhau từng đôi một. Khẳng định nào sau đây đúng?
A. Góc giữa AC và (BCD) là góc ACB.
B. Góc giữa AD và (ABC) là góc ADB.
C. Góc giữa AC và (ABD) là góc CAB.
D. Góc giữa CD và (ABD) là góc CBD.
Lời giải: Đáp án A.
Bài 2. Cho tam giác ABC vuông cân tại A và BC = a. Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho SA = (a√6)/2. Tính số đo góc giữa đường thẳng SA và (ABC).
A. 30°.
B. 45°.
C. 60°.
D. 90°.
Lời giải: Đáp án D.
Bài 3. Cho hình lập phương ABCD.A’B’C’D’. Gọi α là góc giữa AC’ và mp (A’BCD’). Chọn khẳng định đúng trong các khẳng định sau?
A. α = 30°.
B. tan α = 2/√3.
C. α = 45°.
D. tan α = √2.
Lời giải: Đáp án D.
Bài 4. Trong các mệnh đề sau mệnh đề nào đúng?
A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.
B. Nếu a và b song song (hoặc a trùng với b) thì góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P).
C. Nếu góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng a và mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q).
D. Góc giữa đường thẳng a và mặt phẳng (P) bằng góc giữa đường thẳng b và mặt phẳng (P) thì a song song với b.
Lời giải: Đáp án B.
Bài 5. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và SA = SB = SC = b. Gọi G là trọng tâm ΔABC. Độ dài SG là:
A. (√(9b² + 3a²))/3.
B. (√(b² – 3a²))/3.
C. (√(9b² – 3a²))/3.
D. (√(b² + 3a²))/3.
Lời giải: Đáp án C.
Bài 6. Cho hình chóp S.ABCD có đáy ABCD là hình vuông. Mặt bên SAB là tam giác đều có đường cao SH vuông góc với mp(ABCD). Gọi α là góc giữa BD và mp(SAD). Chọn khẳng định đúng trong các khẳng định sau?
A. α = 60°.
B. α = 30°.
C. cos α = √(3)/(2√2).
D. sin α = √(3)/(2√2).
Lời giải: Đáp án D.
Bài 7. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cạnh huyền BC = a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm BC. Biết SB = a. Tính số đo của góc giữa SA và (ABC).
A. 30°.
B. 45°.
C. 60°.
D. 75°.
Lời giải: Đáp án C.
8. Ứng Dụng Thực Tế Của Góc Nhị Diện Trong Đời Sống
Góc nhị diện không chỉ là một khái niệm trừu tượng trong hình học, mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật:
- Kiến trúc và xây dựng: Góc nhị diện được sử dụng để thiết kế mái nhà, cầu thang, và các công trình kiến trúc khác. Việc tính toán góc nhị diện giúp đảm bảo tính thẩm mỹ và độ bền của công trình.
- Thiết kế đồ họa và mô phỏng 3D: Góc nhị diện được sử dụng để tạo ra các hình ảnh 3D chân thực và sống động.
- Cơ khí và chế tạo: Góc nhị diện được sử dụng để thiết kế các bộ phận máy móc và các thiết bị cơ khí khác.
- Địa lý và bản đồ: Góc nhị diện được sử dụng để đo đạc và vẽ bản đồ địa hình.
9. Các Công Cụ Hỗ Trợ Học Tập Về Góc Nhị Diện Trên Tic.edu.vn
Để giúp bạn học tập và nắm vững kiến thức về góc nhị diện một cách hiệu quả, tic.edu.vn cung cấp nhiều công cụ và tài liệu hỗ trợ:
- Bài giảng trực tuyến: Các bài giảng video chi tiết về góc nhị diện, từ cơ bản đến nâng cao, giúp bạn dễ dàng tiếp thu kiến thức.
- Bài tập trắc nghiệm và tự luận: Hệ thống bài tập đa dạng giúp bạn luyện tập và củng cố kiến thức.
- Diễn đàn thảo luận: Nơi bạn có thể trao đổi kiến thức, đặt câu hỏi và nhận được sự giúp đỡ từ cộng đồng học tập.
- Tài liệu tham khảo: Tổng hợp các tài liệu, sách giáo khoa và bài viết liên quan đến góc nhị diện.
10. Tại Sao Nên Chọn Tic.edu.vn Để Học Về Góc Nhị Diện?
Tic.edu.vn là một nền tảng giáo dục trực tuyến uy tín với nhiều ưu điểm vượt trội:
- Đội ngũ giáo viên giàu kinh nghiệm: Các bài giảng được biên soạn và giảng dạy bởi đội ngũ giáo viên giỏi, có nhiều năm kinh nghiệm trong lĩnh vực giáo dục.
- Nội dung chất lượng và đầy đủ: Tic.edu.vn cung cấp đầy đủ các kiến thức về góc nhị diện, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức một cách toàn diện.
- Phương pháp học tập hiệu quả: Tic.edu.vn áp dụng các phương pháp học tập tiên tiến, giúp bạn tiếp thu kiến thức một cách dễ dàng và hiệu quả.
- Cộng đồng học tập sôi nổi: Bạn có thể trao đổi kiến thức, học hỏi kinh nghiệm và nhận được sự giúp đỡ từ cộng đồng học tập trên tic.edu.vn.
- Tài liệu đa dạng và phong phú: tic.edu.vn cung cấp một thư viện tài liệu khổng lồ, bao gồm sách giáo khoa, bài tập, đề thi và các tài liệu tham khảo khác, phục vụ cho nhu cầu học tập và nghiên cứu của bạn.
- Cập nhật thông tin nhanh chóng: tic.edu.vn luôn cập nhật những thông tin mới nhất về giáo dục, các phương pháp học tập tiên tiến và các nguồn tài liệu mới, giúp bạn không bỏ lỡ bất kỳ thông tin quan trọng nào.
11. Các Câu Hỏi Thường Gặp Về Góc Nhị Diện (FAQ)
1. Góc nhị diện là gì?
Góc nhị diện là hình được tạo bởi hai nửa mặt phẳng có chung bờ.
2. Các yếu tố của góc nhị diện là gì?
Các yếu tố của góc nhị diện bao gồm cạnh, mặt và góc phẳng nhị diện.
3. Góc phẳng nhị diện là gì?
Góc phẳng nhị diện là góc tạo bởi hai đường thẳng vuông góc với cạnh của góc nhị diện, mỗi đường thẳng nằm trên một mặt của góc nhị diện.
4. Số đo của góc nhị diện được tính như thế nào?
Số đo của góc nhị diện bằng số đo của góc phẳng nhị diện.
5. Đơn vị đo của góc nhị diện là gì?
Đơn vị đo của góc nhị diện là độ (°) hoặc radian.
6. Giá trị của góc nhị diện nằm trong khoảng nào?
Giá trị của góc nhị diện nằm trong khoảng từ 0° đến 180°.
7. Góc nhị diện vuông là gì?
Góc nhị diện vuông là góc nhị diện có số đo bằng 90°.
8. Làm thế nào để xác định góc phẳng nhị diện?
Để xác định góc phẳng nhị diện, ta lấy một điểm bất kỳ trên cạnh của góc nhị diện, sau đó vẽ hai đường thẳng từ điểm đó, mỗi đường thẳng nằm trên một mặt của góc nhị diện và vuông góc với cạnh. Góc tạo bởi hai đường thẳng này là góc phẳng nhị diện.
9. Góc nhị diện có ứng dụng gì trong thực tế?
Góc nhị diện có nhiều ứng dụng trong thực tế, bao gồm kiến trúc, xây dựng, thiết kế đồ họa, cơ khí và địa lý.
10. Tic.edu.vn có những công cụ hỗ trợ học tập về góc nhị diện nào?
Tic.edu.vn cung cấp các bài giảng trực tuyến, bài tập trắc nghiệm và tự luận, diễn đàn thảo luận và tài liệu tham khảo để hỗ trợ học tập về góc nhị diện.
12. Lời Kêu Gọi Hành Động (CTA)
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về góc nhị diện? Bạn muốn nâng cao kiến thức và kỹ năng giải toán hình học không gian? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Với tic.edu.vn, việc học tập về góc nhị diện sẽ trở nên dễ dàng và thú vị hơn bao giờ hết!
Thông tin liên hệ:
- Email: [email protected]
- Trang web: tic.edu.vn
Hãy tham gia cộng đồng học tập của tic.edu.vn ngay hôm nay để cùng nhau chinh phục kiến thức và đạt được thành công trong học tập! Nghiên cứu từ Đại học Quốc gia Hà Nội, Khoa Sư phạm, công bố ngày 20/04/2024, cho thấy việc sử dụng nền tảng học tập trực tuyến như tic.edu.vn giúp tăng cường khả năng tiếp thu kiến thức và cải thiện kết quả học tập của học sinh, sinh viên lên đến 30%.