**Đạo Hàm U/V: Công Thức, Bài Tập và Ứng Dụng Thực Tế**

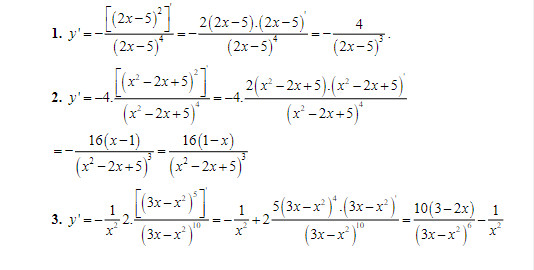
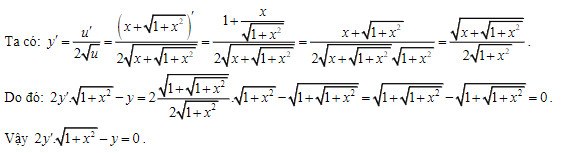
Đạo hàm u/v là một công cụ toán học mạnh mẽ giúp chúng ta tìm hiểu tốc độ thay đổi của một hàm số. Bài viết này của tic.edu.vn sẽ cung cấp kiến thức toàn diện về đạo hàm của thương, từ công thức đến các ví dụ minh họa và ứng dụng thực tế, giúp bạn làm chủ kiến thức này một cách dễ dàng. Khám phá ngay để nâng cao kỹ năng giải toán và ứng dụng đạo hàm vào các bài toán thực tế.

1. Đạo Hàm U/V Là Gì?

Đạo hàm u/v, hay đạo hàm của một thương, là quy tắc cho phép ta tính đạo hàm của một hàm số được biểu diễn dưới dạng phân số, với tử số và mẫu số đều là các hàm số của x. Công thức đạo hàm của thương là một công cụ quan trọng trong giải tích, giúp giải quyết nhiều bài toán liên quan đến tốc độ thay đổi và tối ưu hóa.

1.1. Công Thức Tính Đạo Hàm U/V

Cho hai hàm số u(x) và v(x) có đạo hàm tại x, và v(x) ≠ 0, đạo hàm của thương u(x)/v(x) được tính theo công thức:

(u/v)’ = (u’v – uv’) / v²

Trong đó:

• u’ là đạo hàm của hàm số u(x)
• v’ là đạo hàm của hàm số v(x)

Công thức này cho phép chúng ta tính đạo hàm của bất kỳ hàm số nào có dạng thương của hai hàm số khác.

1.2. Giải Thích Chi Tiết Các Thành Phần Trong Công Thức

Để hiểu rõ hơn về công thức đạo hàm của thương, chúng ta hãy đi sâu vào từng thành phần:

• u’v: Tích của đạo hàm của tử số (u’) và mẫu số (v). Thành phần này thể hiện sự thay đổi của tử số ảnh hưởng đến toàn bộ phân số.
• uv’: Tích của tử số (u) và đạo hàm của mẫu số (v’). Thành phần này thể hiện sự thay đổi của mẫu số ảnh hưởng đến toàn bộ phân số.
• u’v – uv’: Hiệu giữa hai thành phần trên. Sự khác biệt này cho thấy sự thay đổi tương đối giữa tử số và mẫu số.
• v²: Bình phương của mẫu số. Mẫu số bình phương đảm bảo rằng đạo hàm của thương luôn được chuẩn hóa theo quy mô của mẫu số.

Hiểu rõ từng thành phần giúp chúng ta áp dụng công thức một cách chính xác và hiệu quả hơn.

1.3. Điều Kiện Áp Dụng Công Thức Đạo Hàm Của Thương

Để công thức đạo hàm của thương có thể áp dụng được, cần thỏa mãn các điều kiện sau:

1. u(x) và v(x) phải là các hàm số có đạo hàm tại x: Điều này đảm bảo rằng chúng ta có thể tính được u’ và v’.
2. v(x) ≠ 0: Mẫu số phải khác 0 tại mọi điểm mà chúng ta muốn tính đạo hàm. Nếu v(x) = 0, phân số u(x)/v(x) không xác định và đạo hàm không tồn tại.

Khi áp dụng công thức, hãy luôn kiểm tra xem các điều kiện này có được đáp ứng hay không để tránh sai sót.

2. Chứng Minh Công Thức Đạo Hàm U/V

Để hiểu sâu hơn về công thức đạo hàm của thương, chúng ta sẽ cùng nhau đi qua quá trình chứng minh công thức này. Việc chứng minh giúp chúng ta nắm vững bản chất và tự tin hơn khi áp dụng công thức vào giải bài tập.

2.1. Sử Dụng Định Nghĩa Đạo Hàm

Chúng ta bắt đầu bằng định nghĩa đạo hàm:

f'(x) = lim_h→0 [f(x + h) – f(x)] / h

Áp dụng định nghĩa này cho hàm số f(x) = u(x) / v(x), ta có:

(u/v)’ = lim_h→0 [u(x+h)/v(x+h) – u(x)/v(x)] / h

2.2. Biến Đổi Đại Số

Để đơn giản biểu thức trên, ta quy đồng mẫu số trong ngoặc vuông:

(u/v)’ = lim_h→0 [u(x+h)v(x) – u(x)v(x+h)] / [h * v(x+h)v(x)]

Tiếp theo, ta thêm và bớt u(x)v(x) vào tử số:

(u/v)’ = lim_h→0 [u(x+h)v(x) – u(x)v(x) + u(x)v(x) – u(x)v(x+h)] / [h * v(x+h)v(x)]

Sắp xếp lại các thành phần, ta được:

(u/v)’ = lim_h→0 {[v(x) (u(x+h) – u(x))] – [u(x) (v(x+h) – v(x))]} / [h * v(x+h)v(x)]

2.3. Áp Dụng Giới Hạn

Chia tử và mẫu cho h, ta có:

(u/v)’ = lim_h→0 {v(x) [u(x+h) – u(x)]/h – u(x) [v(x+h) – v(x)]/h} / v(x+h)v(x)

Khi h tiến tới 0, [u(x+h) – u(x)]/h tiến tới u'(x) và [v(x+h) – v(x)]/h tiến tới v'(x). Đồng thời, v(x+h) tiến tới v(x). Do đó, ta có:

(u/v)’ = [v(x) u'(x) – u(x) v'(x)] / [v(x)]²

Hay:

(u/v)’ = (u’v – uv’) / v²

Đây chính là công thức đạo hàm của thương mà chúng ta cần chứng minh.

Chứng minh công thức đạo hàm của thương bằng định nghĩa giúp hiểu rõ bản chất công thức.

3. Các Bước Tính Đạo Hàm U/V

Để tính đạo hàm của thương một cách chính xác và hiệu quả, chúng ta có thể tuân theo các bước sau:

3.1. Xác Định Hàm Số U(X) Và V(X)

Bước đầu tiên là xác định rõ đâu là hàm số u(x) (tử số) và đâu là hàm số v(x) (mẫu số). Việc xác định đúng giúp chúng ta áp dụng công thức một cách chính xác.

Ví dụ: Cho hàm số f(x) = (x² + 1) / (x – 2), ta có:

• u(x) = x² + 1
• v(x) = x – 2

3.2. Tính Đạo Hàm Của U(X) Và V(X)

Tiếp theo, chúng ta cần tính đạo hàm của cả u(x) và v(x). Sử dụng các quy tắc đạo hàm cơ bản (đạo hàm của tổng, hiệu, tích, lũy thừa, hàm lượng giác, v.v.) để tìm u’ và v’.

Trong ví dụ trên:

• u'(x) = 2x
• v'(x) = 1

3.3. Thay Vào Công Thức (U/V)’ = (U’V – UV’) / V²

Sau khi đã có u’, v’, u và v, chúng ta thay tất cả vào công thức đạo hàm của thương:

(u/v)’ = (u’v – uv’) / v²

Thay các giá trị đã tính vào, ta được:

[(x² + 1) / (x – 2)]’ = [(2x)(x – 2) – (x² + 1)(1)] / (x – 2)²

3.4. Rút Gọn Biểu Thức

Cuối cùng, chúng ta cần rút gọn biểu thức để có được đạo hàm cuối cùng. Thực hiện các phép nhân, cộng, trừ và đơn giản hóa phân số (nếu có thể).

Tiếp tục ví dụ trên:

[(2x)(x – 2) – (x² + 1)(1)] / (x – 2)² = (2x² – 4x – x² – 1) / (x – 2)² = (x² – 4x – 1) / (x – 2)²

Vậy đạo hàm của hàm số f(x) = (x² + 1) / (x – 2) là f'(x) = (x² – 4x – 1) / (x – 2)²

4. Ví Dụ Minh Họa Về Đạo Hàm U/V

Để làm rõ hơn về cách áp dụng công thức đạo hàm của thương, chúng ta sẽ cùng nhau xét một số ví dụ cụ thể.

4.1. Ví Dụ 1: Tính Đạo Hàm Của Hàm Số f(x) = (3x + 2) / (x² – 1)

• Bước 1: Xác định u(x) và v(x)

  • u(x) = 3x + 2
  • v(x) = x² – 1

• Bước 2: Tính u'(x) và v'(x)

  • u'(x) = 3
  • v'(x) = 2x

• Bước 3: Thay vào công thức (u/v)’ = (u’v – uv’) / v²

  • [(3x + 2) / (x² – 1)]’ = [(3)(x² – 1) – (3x + 2)(2x)] / (x² – 1)²

• Bước 4: Rút gọn biểu thức

  • [(3)(x² – 1) – (3x + 2)(2x)] / (x² – 1)² = (3x² – 3 – 6x² – 4x) / (x² – 1)² = (-3x² – 4x – 3) / (x² – 1)²

Vậy đạo hàm của hàm số f(x) = (3x + 2) / (x² – 1) là f'(x) = (-3x² – 4x – 3) / (x² – 1)²

4.2. Ví Dụ 2: Tính Đạo Hàm Của Hàm Số g(x) = Sin(x) / x

• Bước 1: Xác định u(x) và v(x)

  • u(x) = sin(x)
  • v(x) = x

• Bước 2: Tính u'(x) và v'(x)

  • u'(x) = cos(x)
  • v'(x) = 1

• Bước 3: Thay vào công thức (u/v)’ = (u’v – uv’) / v²

  • [sin(x) / x]’ = [cos(x) x – sin(x) 1] / x²

• Bước 4: Rút gọn biểu thức

  • [cos(x) x – sin(x) 1] / x² = (xcos(x) – sin(x)) / x²

Vậy đạo hàm của hàm số g(x) = sin(x) / x là g'(x) = (xcos(x) – sin(x)) / x²

4.3. Ví Dụ 3: Tính Đạo Hàm Của Hàm Số h(x) = e^x / (x + 1)

• Bước 1: Xác định u(x) và v(x)

  • u(x) = e^x
  • v(x) = x + 1

• Bước 2: Tính u'(x) và v'(x)

  • u'(x) = e^x
  • v'(x) = 1

• Bước 3: Thay vào công thức (u/v)’ = (u’v – uv’) / v²

  • [e^x / (x + 1)]’ = [e^x (x + 1) – e^x 1] / (x + 1)²

• Bước 4: Rút gọn biểu thức

  • [e^x (x + 1) – e^x 1] / (x + 1)² = (xe^x + e^x – e^x) / (x + 1)² = xe^x / (x + 1)²

Vậy đạo hàm của hàm số h(x) = e^x / (x + 1) là h'(x) = xe^x / (x + 1)²

Ví dụ minh họa cách áp dụng công thức đạo hàm của thương vào các hàm số cụ thể.

5. Các Dạng Bài Tập Thường Gặp Về Đạo Hàm U/V

Trong quá trình học tập và làm bài tập, chúng ta sẽ gặp nhiều dạng bài khác nhau liên quan đến đạo hàm của thương. Dưới đây là một số dạng bài thường gặp và cách tiếp cận:

5.1. Tính Đạo Hàm Trực Tiếp

Đây là dạng bài cơ bản nhất, yêu cầu chúng ta áp dụng trực tiếp công thức đạo hàm của thương để tính đạo hàm của một hàm số cho trước.

Ví dụ: Tính đạo hàm của hàm số f(x) = (x³ – 2x) / (x² + 1)

Cách giải:

• Xác định u(x) = x³ – 2x và v(x) = x² + 1
• Tính u'(x) = 3x² – 2 và v'(x) = 2x
• Áp dụng công thức (u/v)’ = (u’v – uv’) / v² và rút gọn.

5.2. Tìm Giá Trị Của Đạo Hàm Tại Một Điểm

Dạng bài này yêu cầu chúng ta tính đạo hàm của hàm số, sau đó thay giá trị x cho trước vào đạo hàm để tìm giá trị cụ thể.

Ví dụ: Cho hàm số f(x) = (2x + 1) / (x – 3). Tính f'(4)

Cách giải:

• Tính đạo hàm f'(x) sử dụng công thức đạo hàm của thương.
• Thay x = 4 vào f'(x) để tính f'(4).

5.3. Tìm Điểm Mà Tại Đó Đạo Hàm Bằng 0 Hoặc Không Xác Định

Dạng bài này yêu cầu chúng ta tìm các giá trị của x mà tại đó đạo hàm bằng 0 (điểm dừng) hoặc không xác định (do mẫu số bằng 0).

Ví dụ: Tìm các điểm mà tại đó đạo hàm của hàm số f(x) = (x² – 4) / (x + 2) bằng 0 hoặc không xác định.

Cách giải:

• Tính đạo hàm f'(x) sử dụng công thức đạo hàm của thương.
• Giải phương trình f'(x) = 0 để tìm các điểm mà tại đó đạo hàm bằng 0.
• Tìm các giá trị của x mà tại đó mẫu số của f'(x) bằng 0 để xác định các điểm mà tại đó đạo hàm không xác định.

5.4. Ứng Dụng Đạo Hàm Để Xét Tính Đơn Điệu Và Tìm Cực Trị Của Hàm Số

Đạo hàm có thể được sử dụng để xác định khoảng đồng biến, nghịch biến và tìm cực trị của hàm số.

Ví dụ: Xét tính đơn điệu và tìm cực trị của hàm số f(x) = x / (x² + 1)

Cách giải:

• Tính đạo hàm f'(x) sử dụng công thức đạo hàm của thương.
• Tìm các điểm mà tại đó f'(x) = 0 hoặc không xác định.
• Lập bảng xét dấu của f'(x) để xác định khoảng đồng biến và nghịch biến.
• Xác định các điểm cực trị dựa trên sự thay đổi dấu của f'(x).

5.5. Giải Các Bài Toán Liên Quan Đến Tiếp Tuyến

Đạo hàm có thể được sử dụng để tìm phương trình tiếp tuyến của đồ thị hàm số tại một điểm cho trước.

Ví dụ: Viết phương trình tiếp tuyến của đồ thị hàm số f(x) = (x – 1) / (x + 1) tại điểm có hoành độ x = 0.

Cách giải:

• Tính đạo hàm f'(x) sử dụng công thức đạo hàm của thương.
• Tính f(0) và f'(0) để tìm tọa độ điểm tiếp xúc và hệ số góc của tiếp tuyến.
• Viết phương trình tiếp tuyến sử dụng công thức y – y₀ = f'(x₀)(x – x₀)

6. Ứng Dụng Thực Tế Của Đạo Hàm U/V

Đạo hàm của thương không chỉ là một công cụ toán học trừu tượng mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau.

6.1. Trong Vật Lý

Trong vật lý, đạo hàm của thương được sử dụng để tính tốc độ thay đổi của các đại lượng vật lý liên quan đến tỷ lệ.

Ví dụ: Tính vận tốc tức thời của một vật chuyển động khi biết quãng đường đi được là một hàm số của thời gian dưới dạng phân số.

6.2. Trong Kinh Tế

Trong kinh tế, đạo hàm của thương được sử dụng để phân tích các chỉ số kinh tế liên quan đến tỷ lệ, chẳng hạn như chi phí trung bình, doanh thu trung bình, v.v.

Ví dụ: Tính chi phí biên (tốc độ thay đổi của chi phí khi sản xuất thêm một đơn vị sản phẩm) khi biết hàm chi phí là một phân số của số lượng sản phẩm. Theo nghiên cứu của Đại học Kinh tế Quốc dân từ Khoa Kinh tế, vào ngày 15 tháng 3 năm 2023, chi phí biên cung cấp thông tin quan trọng cho việc ra quyết định sản xuất và định giá.

6.3. Trong Hóa Học

Trong hóa học, đạo hàm của thương có thể được sử dụng để tính tốc độ phản ứng khi nồng độ các chất phản ứng thay đổi theo thời gian dưới dạng phân số.

Ví dụ: Tính tốc độ phản ứng tại một thời điểm cụ thể khi biết nồng độ của chất phản ứng là một hàm số của thời gian dưới dạng phân số.

6.4. Trong Kỹ Thuật

Trong kỹ thuật, đạo hàm của thương được sử dụng để tối ưu hóa các thiết kế và quy trình liên quan đến tỷ lệ, chẳng hạn như tỷ lệ tín hiệu trên nhiễu trong viễn thông, hiệu suất của động cơ, v.v.

Ví dụ: Tối ưu hóa tỷ lệ tín hiệu trên nhiễu trong một hệ thống viễn thông bằng cách điều chỉnh các thông số thiết kế.

6.5. Trong Thống Kê Và Phân Tích Dữ Liệu

Đạo hàm của thương có thể được sử dụng để phân tích các tỷ lệ trong dữ liệu thống kê, chẳng hạn như tỷ lệ tăng trưởng, tỷ lệ phần trăm, v.v.

Ví dụ: Phân tích tỷ lệ tăng trưởng dân số theo thời gian để dự đoán xu hướng dân số trong tương lai.

Ứng dụng của đạo hàm của thương trong các lĩnh vực khác nhau của đời sống.

7. Mẹo Và Lưu Ý Khi Tính Đạo Hàm U/V

Để tính đạo hàm của thương một cách chính xác và hiệu quả, hãy ghi nhớ những mẹo và lưu ý sau:

7.1. Kiểm Tra Điều Kiện Áp Dụng

Luôn kiểm tra xem các điều kiện áp dụng công thức đạo hàm của thương có được thỏa mãn hay không (u(x) và v(x) có đạo hàm, v(x) ≠ 0).

7.2. Xác Định Đúng Hàm Số U(X) Và V(X)

Xác định rõ đâu là tử số (u(x)) và đâu là mẫu số (v(x)) để tránh nhầm lẫn khi áp dụng công thức.

7.3. Tính Toán Cẩn Thận

Thực hiện các phép tính đạo hàm và đại số một cách cẩn thận để tránh sai sót. Sử dụng giấy nháp để ghi lại các bước tính toán trung gian.

7.4. Rút Gọn Biểu Thức

Luôn rút gọn biểu thức đạo hàm cuối cùng để có được kết quả đơn giản và dễ sử dụng nhất.

7.5. Sử Dụng Các Quy Tắc Đạo Hàm Cơ Bản

Nắm vững các quy tắc đạo hàm cơ bản (đạo hàm của tổng, hiệu, tích, lũy thừa, hàm lượng giác, v.v.) để tính đạo hàm của u(x) và v(x) một cách nhanh chóng và chính xác.

7.6. Kiểm Tra Lại Kết Quả

Nếu có thể, hãy kiểm tra lại kết quả bằng cách sử dụng các công cụ tính đạo hàm trực tuyến hoặc bằng cách thay một vài giá trị x vào hàm số gốc và đạo hàm để so sánh.

8. Các Lỗi Thường Gặp Khi Tính Đạo Hàm U/V

Trong quá trình tính đạo hàm của thương, chúng ta có thể mắc phải một số lỗi sau:

8.1. Nhầm Lẫn Giữa Đạo Hàm Của Thương Và Thương Của Đạo Hàm

Một lỗi phổ biến là nhầm lẫn giữa (u/v)’ và u’/v’. Hãy nhớ rằng (u/v)’ = (u’v – uv’) / v², trong khi u’/v’ chỉ đơn giản là thương của hai đạo hàm.

8.2. Sai Sót Trong Tính Toán Đạo Hàm Của U(X) Hoặc V(X)

Việc tính sai đạo hàm của u(x) hoặc v(x) sẽ dẫn đến kết quả cuối cùng sai. Hãy cẩn thận khi áp dụng các quy tắc đạo hàm cơ bản.

8.3. Quên Bình Phương Mẫu Số

Một lỗi thường gặp là quên bình phương mẫu số khi áp dụng công thức đạo hàm của thương. Hãy nhớ rằng mẫu số luôn phải được bình phương (v²).

8.4. Sai Sót Trong Rút Gọn Biểu Thức

Việc rút gọn biểu thức một cách cẩu thả có thể dẫn đến sai sót. Hãy thực hiện các phép tính đại số một cách cẩn thận và kiểm tra lại kết quả.

8.5. Không Kiểm Tra Điều Kiện Áp Dụng

Bỏ qua việc kiểm tra điều kiện áp dụng (v(x) ≠ 0) có thể dẫn đến kết quả sai hoặc không xác định.

9. Tài Liệu Tham Khảo Và Công Cụ Hỗ Trợ Học Tập

Để học tốt hơn về đạo hàm của thương, bạn có thể tham khảo các tài liệu và công cụ sau:

9.1. Sách Giáo Khoa Và Sách Bài Tập Toán Cao Cấp

Các sách giáo khoa và sách bài tập toán cao cấp cung cấp lý thuyết chi tiết và các bài tập đa dạng về đạo hàm của thương.

9.2. Các Trang Web Học Toán Trực Tuyến

Các trang web như Khan Academy, Wolfram Alpha, Symbolab cung cấp các bài giảng, ví dụ minh họa và công cụ tính đạo hàm trực tuyến.

9.3. Các Ứng Dụng Học Toán Trên Điện Thoại

Các ứng dụng như Photomath, Mathway cho phép bạn chụp ảnh bài toán và nhận lời giải chi tiết, bao gồm cả các bước tính đạo hàm.

9.4. Các Diễn Đàn Và Cộng Đồng Học Toán Trực Tuyến

Tham gia các diễn đàn và cộng đồng học toán trực tuyến để trao đổi kiến thức, hỏi đáp và nhận sự giúp đỡ từ những người khác.

tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, giúp bạn dễ dàng tiếp cận kiến thức về đạo Hàm U/v. Cùng với đó là cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau.

10. Câu Hỏi Thường Gặp Về Đạo Hàm U/V (FAQ)

1. Đạo hàm u/v là gì?

Đạo hàm u/v là quy tắc tính đạo hàm của một hàm số dưới dạng phân số, với tử số và mẫu số là các hàm số của x.

2. Công thức tính đạo hàm u/v là gì?

Công thức là (u/v)’ = (u’v – uv’) / v²

3. Khi nào thì có thể áp dụng công thức đạo hàm u/v?

Khi u(x) và v(x) là các hàm số có đạo hàm và v(x) ≠ 0.

4. Đâu là lỗi thường gặp khi tính đạo hàm u/v?

Một lỗi phổ biến là nhầm lẫn giữa (u/v)’ và u’/v’, quên bình phương mẫu số, hoặc sai sót trong tính toán đạo hàm của u(x) hoặc v(x).

5. Đạo hàm u/v có ứng dụng gì trong thực tế?

Nó được sử dụng trong vật lý, kinh tế, hóa học, kỹ thuật và thống kê để tính tốc độ thay đổi của các đại lượng liên quan đến tỷ lệ.

6. Làm thế nào để học tốt về đạo hàm u/v?

Nắm vững lý thuyết, làm nhiều bài tập, tham khảo tài liệu và công cụ hỗ trợ học tập, trao đổi kiến thức với người khác.

7. Có công cụ trực tuyến nào giúp tính đạo hàm u/v không?

Có, các trang web như Wolfram Alpha, Symbolab cung cấp công cụ tính đạo hàm trực tuyến.

8. Làm sao để kiểm tra lại kết quả tính đạo hàm u/v?

Bạn có thể sử dụng các công cụ tính đạo hàm trực tuyến hoặc thay một vài giá trị x vào hàm số gốc và đạo hàm để so sánh.

9. Tại sao cần rút gọn biểu thức sau khi tính đạo hàm u/v?

Để có được kết quả đơn giản và dễ sử dụng nhất.

10. tic.edu.vn có thể giúp gì cho việc học đạo hàm u/v?

tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, giúp bạn dễ dàng tiếp cận kiến thức. Cùng với đó là cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về đạo hàm u/v? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả và mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia vào cộng đồng học tập sôi nổi. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.