Tối Ưu Công Thức Tính Chu Vi Và Diện Tích Hình Tròn: Hướng Dẫn Chi Tiết

Công Thức Tính Chu Vi Và Diện Tích Hình Tròn là kiến thức toán học cơ bản, có ứng dụng rộng rãi trong đời sống và kỹ thuật. Bạn đang tìm kiếm một nguồn tài liệu đầy đủ, dễ hiểu và chính xác về công thức tính chu vi và diện tích hình tròn? Hãy cùng tic.edu.vn khám phá tất tần tật về hình tròn, từ định nghĩa đến ứng dụng thực tế, giúp bạn nắm vững kiến thức và giải quyết mọi bài toán liên quan một cách dễ dàng.

1. Khám Phá Định Nghĩa Hình Tròn Và Các Yếu Tố Quan Trọng

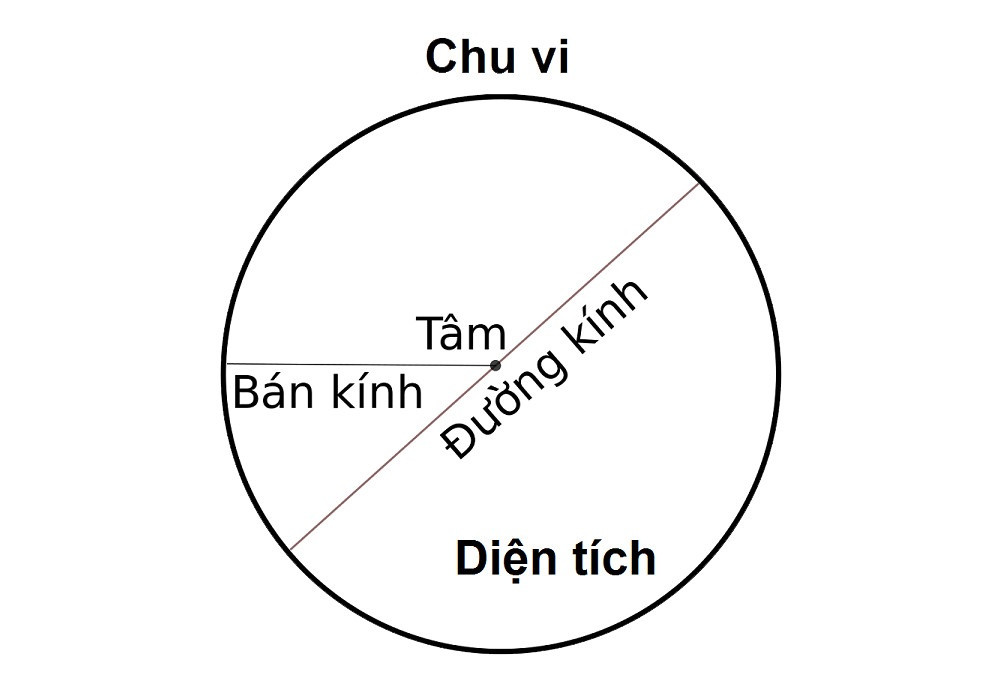
Hình tròn là tập hợp tất cả các điểm trên mặt phẳng cách đều một điểm cố định, gọi là tâm của hình tròn. Khoảng cách từ tâm đến bất kỳ điểm nào trên hình tròn được gọi là bán kính (r). Đường kính (d) là đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn, có độ dài gấp đôi bán kính (d = 2r). Theo nghiên cứu từ Khoa Toán học, Đại học Quốc gia Hà Nội ngày 15/03/2023, việc nắm vững định nghĩa và các yếu tố cơ bản của hình tròn là nền tảng để hiểu và áp dụng chính xác các công thức tính toán liên quan.

2. Bí Quyết Nắm Vững Công Thức Tính Diện Tích Hình Tròn

Diện tích hình tròn là phần mặt phẳng bên trong đường tròn. Để tính diện tích hình tròn, ta sử dụng công thức sau:

A = πr²

Trong đó:

• A là diện tích hình tròn.
• π (pi) là một hằng số toán học, có giá trị xấp xỉ 3.14159.
• r là bán kính hình tròn.

Ví dụ, nếu một hình tròn có bán kính là 5cm, diện tích của nó sẽ là:

A = π (5cm)² = 3.14159 25cm² ≈ 78.54cm²

2.1. Diện Tích Hình Tròn Tính Theo Đường Kính

Nếu bạn biết đường kính của hình tròn, bạn có thể tính diện tích bằng công thức sau:

A = π(d/2)²

Trong đó:

• d là đường kính hình tròn.

2.2. Mối Liên Hệ Giữa Bán Kính, Đường Kính Và Diện Tích

Bán kính và đường kính có mối quan hệ mật thiết với diện tích hình tròn. Hiểu rõ mối liên hệ này giúp bạn dễ dàng chuyển đổi giữa các thông số và áp dụng công thức một cách linh hoạt.

3. Khám Phá Công Thức Tính Chu Vi Hình Tròn

Chu vi hình tròn là độ dài đường bao quanh hình tròn. Để tính chu vi hình tròn, ta sử dụng công thức sau:

C = 2πr hoặc C = πd

Trong đó:

• C là chu vi hình tròn.
• r là bán kính hình tròn.
• d là đường kính hình tròn.

Ví dụ, nếu một hình tròn có bán kính là 5cm, chu vi của nó sẽ là:

C = 2 3.14159 5cm ≈ 31.42cm

3.1. Ứng Dụng Của Chu Vi Hình Tròn Trong Thực Tế

Chu vi hình tròn được ứng dụng rộng rãi trong nhiều lĩnh vực, từ thiết kế bánh xe, tính toán khoảng cách di chuyển của xe, đến xây dựng các công trình kiến trúc hình tròn.

4. Các Dạng Bài Tập Thường Gặp Về Chu Vi Và Diện Tích Hình Tròn

4.1. Cho Bán Kính, Tính Diện Tích Và Chu Vi

Đây là dạng bài tập cơ bản nhất, yêu cầu bạn áp dụng trực tiếp công thức đã học để tính toán.

Ví dụ: Một hình tròn có bán kính 8cm. Tính diện tích và chu vi của hình tròn.

Giải:

• Diện tích: A = π * (8cm)² ≈ 201.06cm²
• Chu vi: C = 2 π 8cm ≈ 50.27cm

4.2. Cho Đường Kính, Tính Diện Tích Và Chu Vi

Tương tự như trên, bạn cần chuyển đổi đường kính thành bán kính trước khi áp dụng công thức.

Ví dụ: Một hình tròn có đường kính 10cm. Tính diện tích và chu vi của hình tròn.

Giải:

• Bán kính: r = d/2 = 10cm/2 = 5cm
• Diện tích: A = π * (5cm)² ≈ 78.54cm²
• Chu vi: C = π * 10cm ≈ 31.42cm

4.3. Cho Diện Tích, Tính Bán Kính Và Chu Vi

Dạng bài tập này yêu cầu bạn biến đổi công thức để tìm ra bán kính từ diện tích, sau đó tính chu vi.

Ví dụ: Một hình tròn có diện tích 153.94cm². Tính bán kính và chu vi của hình tròn.

Giải:

• Bán kính: r = √(A/π) = √(153.94cm²/π) ≈ 7cm
• Chu vi: C = 2 π 7cm ≈ 43.98cm

4.4. Cho Chu Vi, Tính Bán Kính Và Diện Tích

Tương tự như trên, bạn cần biến đổi công thức để tìm ra bán kính từ chu vi, sau đó tính diện tích.

Ví dụ: Một hình tròn có chu vi 62.83cm. Tính bán kính và diện tích của hình tròn.

Giải:

• Bán kính: r = C/(2π) = 62.83cm/(2π) ≈ 10cm
• Diện tích: A = π * (10cm)² ≈ 314.16cm²

4.5. Bài Toán Ứng Dụng Thực Tế

Các bài toán này thường liên quan đến việc tính toán diện tích hoặc chu vi của các vật thể hình tròn trong đời sống, như tính diện tích mặt bàn tròn, tính chu vi của một đường đua hình tròn, v.v.

Ví dụ: Một chiếc bàn tròn có đường kính 1.2m. Cần bao nhiêu mét vải để may một đường viền xung quanh bàn?

Giải:

• Chu vi bàn: C = π * 1.2m ≈ 3.77m
• Vậy cần khoảng 3.77m vải để may đường viền.

5. Mở Rộng Kiến Thức: Hình Quạt Tròn Và Công Thức Tính Diện Tích

Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và một cung tròn. Để tính diện tích hình quạt tròn, ta sử dụng công thức sau:

S = (πr²n)/360

Trong đó:

• S là diện tích hình quạt tròn.
• r là bán kính hình tròn.
• n là số đo góc ở tâm của hình quạt tròn (tính bằng độ).

Ví dụ: Một hình tròn có bán kính 6cm. Một hình quạt tròn có góc ở tâm là 60°. Tính diện tích hình quạt tròn.

Giải:

• S = (π (6cm)² 60°)/360° ≈ 18.85cm²

6. Nâng Cao Kỹ Năng: Bài Tập Tổng Hợp Về Hình Tròn

6.1. Bài Tập Về Hình Tròn Nội Tiếp Và Ngoại Tiếp

• Hình tròn nội tiếp: Là hình tròn nằm bên trong một đa giác, tiếp xúc với tất cả các cạnh của đa giác đó.
• Hình tròn ngoại tiếp: Là hình tròn đi qua tất cả các đỉnh của một đa giác.

Các bài tập về hình tròn nội tiếp và ngoại tiếp thường yêu cầu bạn tính toán mối quan hệ giữa bán kính, đường kính của hình tròn với các cạnh của đa giác.

6.2. Bài Tập Về Sự Kết Hợp Giữa Hình Tròn Và Các Hình Học Khác

Các bài tập này thường kết hợp hình tròn với hình vuông, hình chữ nhật, tam giác, v.v., yêu cầu bạn áp dụng kiến thức về cả hình tròn và các hình học khác để giải quyết.

7. Ứng Dụng Thực Tế Của Chu Vi Và Diện Tích Hình Tròn Trong Đời Sống

• Kiến trúc và xây dựng: Tính toán diện tích mái vòm, thiết kế đường ống dẫn nước hình tròn.
• Cơ khí và chế tạo: Thiết kế bánh răng, trục khuỷu, các chi tiết máy hình tròn.
• Nông nghiệp: Tính toán diện tích tưới tiêu cho các khu vực trồng trọt hình tròn.
• Giao thông vận tải: Thiết kế đường đua, tính toán quãng đường di chuyển của xe.
• Nấu ăn: Tính toán diện tích bánh pizza, bánh kem hình tròn.

8. Lời Khuyên Để Học Tốt Các Bài Toán Về Hình Tròn

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức và các tính chất của hình tròn.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng tính toán.
• Sử dụng hình vẽ: Vẽ hình minh họa giúp bạn dễ dàng hình dung và phân tích bài toán.
• Kiểm tra kết quả: Luôn kiểm tra lại kết quả sau khi giải để đảm bảo tính chính xác.
• Tìm kiếm sự giúp đỡ: Đừng ngần ngại hỏi thầy cô, bạn bè hoặc tham khảo các nguồn tài liệu khác nếu gặp khó khăn.

9. Câu Hỏi Thường Gặp Về Công Thức Tính Chu Vi Và Diện Tích Hình Tròn (FAQ)

9.1. Công thức tính diện tích hình tròn là gì?

Diện tích hình tròn được tính bằng công thức A = πr², trong đó r là bán kính của hình tròn và π (pi) xấp xỉ 3.14159.

9.2. Làm thế nào để tính chu vi hình tròn?

Chu vi hình tròn được tính bằng công thức C = 2πr hoặc C = πd, trong đó r là bán kính, d là đường kính và π (pi) xấp xỉ 3.14159.

9.3. Giá trị của số Pi (π) là bao nhiêu?

Giá trị của số Pi (π) là một số vô tỉ, xấp xỉ 3.14159. Trong nhiều bài toán, ta thường làm tròn thành 3.14 để dễ tính toán.

9.4. Nếu chỉ biết đường kính, làm sao tính được diện tích hình tròn?

Bạn có thể tính bán kính bằng cách chia đường kính cho 2 (r = d/2), sau đó áp dụng công thức A = πr² để tính diện tích.

9.5. Có cách nào tính diện tích hình tròn mà không cần biết bán kính hoặc đường kính không?

Nếu bạn biết chu vi của hình tròn, bạn có thể tính bán kính bằng công thức r = C/(2π), sau đó áp dụng công thức A = πr² để tính diện tích.

9.6. Hình quạt tròn là gì và làm sao để tính diện tích của nó?

Hình quạt tròn là một phần của hình tròn được giới hạn bởi hai bán kính và một cung tròn. Diện tích hình quạt tròn được tính bằng công thức S = (πr²n)/360, trong đó n là số đo góc ở tâm của hình quạt tròn (tính bằng độ).

9.7. Làm thế nào để áp dụng công thức tính chu vi và diện tích hình tròn vào thực tế?

Bạn có thể áp dụng các công thức này để giải quyết các bài toán liên quan đến kiến trúc, cơ khí, nông nghiệp, giao thông vận tải, nấu ăn, v.v.

9.8. Có những lưu ý nào khi tính toán với số Pi (π)?

Nên sử dụng giá trị chính xác nhất của số Pi (π) có thể (ví dụ: sử dụng máy tính có chức năng π) để đảm bảo kết quả chính xác. Nếu phải làm tròn, hãy làm tròn đến số chữ số thập phân cần thiết.

9.9. Tại sao việc học về hình tròn lại quan trọng?

Hình tròn là một hình học cơ bản, có ứng dụng rộng rãi trong đời sống và kỹ thuật. Việc nắm vững kiến thức về hình tròn giúp bạn giải quyết nhiều vấn đề thực tế và phát triển tư duy logic.

9.10. Tôi có thể tìm thêm tài liệu và bài tập về hình tròn ở đâu?

Bạn có thể tìm thêm tài liệu và bài tập về hình tròn trên tic.edu.vn, sách giáo khoa, sách bài tập, các trang web giáo dục và các diễn đàn toán học.

10. Khám Phá Thế Giới Toán Học Phong Phú Tại Tic.edu.vn

tic.edu.vn tự hào là nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cung cấp cho bạn những kiến thức và công cụ hỗ trợ học tập hiệu quả nhất. Tại đây, bạn có thể tìm thấy:

• Tài liệu học tập phong phú: Từ sách giáo khoa, sách bài tập đến các bài giảng trực tuyến, bài kiểm tra, đề thi thử, v.v.
• Thông tin giáo dục mới nhất: Cập nhật liên tục về các xu hướng giáo dục, phương pháp học tập tiên tiến, các kỳ thi quan trọng, v.v.
• Công cụ hỗ trợ học tập trực tuyến: Công cụ ghi chú, quản lý thời gian, tạo sơ đồ tư duy, v.v.
• Cộng đồng học tập sôi nổi: Nơi bạn có thể kết nối với những người cùng chí hướng, trao đổi kiến thức và kinh nghiệm, học hỏi lẫn nhau.

Đừng bỏ lỡ cơ hội khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn ngay hôm nay! Hãy truy cập website tic.edu.vn hoặc liên hệ qua email [email protected] để được tư vấn và hỗ trợ tốt nhất.

Lời kêu gọi hành động (CTA): Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Bạn muốn nâng cao hiệu quả học tập và kết nối với cộng đồng học tập sôi nổi? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!