Công Thức Nhị Thức Newton: Ứng Dụng, Ví Dụ Và Bài Tập

Công Thức Nhị Thức Newton là một công cụ mạnh mẽ trong toán học, cho phép khai triển biểu thức lũy thừa một cách dễ dàng, và tic.edu.vn sẽ giúp bạn nắm vững kiến thức này thông qua các bài viết chi tiết, ví dụ minh họa và bài tập đa dạng. Bài viết này sẽ cung cấp cho bạn cái nhìn tổng quan về định nghĩa, ứng dụng và lợi ích của công thức này.

1. Định Nghĩa và Công Thức Nhị Thức Newton

1.1. Công Thức Tổng Quát

Công thức nhị thức Newton là một công thức toán học quan trọng cho phép khai triển một biểu thức có dạng (a + b)ⁿ, trong đó a và b là các số thực hoặc biểu thức đại số, và n là một số nguyên dương. Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, công thức này cung cấp một phương pháp hệ thống để mở rộng biểu thức thành một tổng các số hạng.

Công thức nhị thức Newton có dạng như sau:

(a + b)ⁿ = ∑_k=0ⁿ C(n, k) a^n-k b^k

Trong đó:

• a, b: Là các số thực hoặc biểu thức đại số.
• n: Là một số nguyên dương (n ≥ 0).
• k: Là chỉ số chạy từ 0 đến n.
• C(n, k): Là tổ hợp chập k của n, được tính bằng công thức: C(n, k) = n! / (k! * (n-k)!)
• ∑: Ký hiệu tổng, biểu thị việc cộng tất cả các số hạng từ k = 0 đến k = n.

Công thức này có thể được viết khai triển ra như sau:

(a + b)ⁿ = C(n, 0) aⁿ + C(n, 1) a^n-1 b + C(n, 2) a^n-2 b² + … + C(n, k) a^n-k b^k + … + C(n, n) bⁿ

1.2. Các Tính Chất Quan Trọng

Công thức nhị thức Newton không chỉ là một công cụ khai triển, mà còn ẩn chứa nhiều tính chất thú vị và hữu ích.

• Số lượng số hạng: Khai triển (a + b)ⁿ luôn có n + 1 số hạng. Điều này giúp ta dễ dàng kiểm tra xem khai triển đã đầy đủ hay chưa.
• Quy luật số mũ: Trong mỗi số hạng, tổng số mũ của a và b luôn bằng n. Số mũ của a giảm dần từ n về 0, trong khi số mũ của b tăng dần từ 0 đến n.
• Tính đối xứng của hệ số: Các hệ số C(n, k) có tính đối xứng, tức là C(n, k) = C(n, n-k). Điều này có nghĩa là hệ số của số hạng đầu tiên bằng hệ số của số hạng cuối cùng, hệ số của số hạng thứ hai bằng hệ số của số hạng áp chót, và cứ tiếp tục như vậy.
• Số hạng tổng quát: Số hạng thứ k + 1 trong khai triển có dạng: T_k+1 = C(n, k) a^n-k b^k. Công thức này rất hữu ích khi ta muốn tìm một số hạng cụ thể trong khai triển mà không cần phải khai triển toàn bộ.

1.3. Hệ Quả Quan Trọng

Từ công thức nhị thức Newton, ta có thể suy ra một số hệ quả quan trọng, thường được sử dụng trong các bài toán:

• Tổng các hệ số: Nếu thay a = b = 1 vào công thức, ta được: 2ⁿ = C(n, 0) + C(n, 1) + … + C(n, n). Hệ quả này cho biết tổng tất cả các hệ số trong khai triển bằng 2 mũ n.
• Tổng các hệ số với dấu xen kẽ: Nếu thay a = 1 và b = -1 vào công thức, ta được: 0 = C(n, 0) – C(n, 1) + C(n, 2) – … + (-1)ⁿC(n, n). Hệ quả này cho biết tổng các hệ số với dấu xen kẽ bằng 0.

1.4. Tam Giác Pascal

Tam giác Pascal là một cách trực quan để biểu diễn các hệ số nhị thức C(n, k). Mỗi hàng của tam giác Pascal tương ứng với một giá trị của n, và các số trong hàng đó là các hệ số C(n, k) tương ứng với k = 0, 1, …, n.

Cách xây dựng tam giác Pascal rất đơn giản:

1. Hàng đầu tiên chỉ có số 1.
2. Các hàng tiếp theo được tạo ra bằng cách cộng hai số liền kề ở hàng trên. Các số ở hai đầu hàng luôn là 1.

Ví dụ, tam giác Pascal cho đến hàng thứ 5 như sau:

      1
    1   1
  1   2   1
1   3   3   1

Các số trong tam giác Pascal chính là các hệ số nhị thức. Ví dụ, hàng thứ 4 (1 3 3 1) tương ứng với các hệ số trong khai triển (a + b)³: 1a³ + 3a²b + 3ab² + 1b³.

Sử dụng tam giác Pascal giúp ta nhanh chóng tìm được các hệ số nhị thức mà không cần phải tính toán bằng công thức tổ hợp.

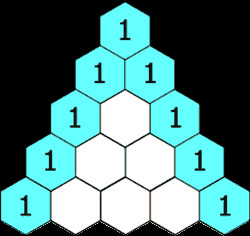Tam giác Pascal minh họa các hệ số nhị thức

**1.5. Mở Rộng cho Số Mũ Âm và Không Nguyên

Mặc dù công thức nhị thức Newton ban đầu được định nghĩa cho số mũ nguyên dương, nó có thể được mở rộng cho số mũ âm và không nguyên thông qua khai triển Taylor hoặc khai triển Maclaurin. Tuy nhiên, trong trường hợp này, khai triển trở thành một chuỗi vô hạn.

2. Ứng Dụng Thực Tế của Công Thức Nhị Thức Newton

Công thức nhị thức Newton không chỉ là một công cụ lý thuyết, nó còn có rất nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau.

2.1. Toán Học

• Giải các bài toán tổ hợp: Công thức nhị thức Newton liên hệ mật thiết với các bài toán tổ hợp. Nó giúp ta tính số lượng các tổ hợp, chỉnh hợp, và giải các bài toán liên quan đến xác suất.
• Chứng minh các đẳng thức: Công thức nhị thức Newton có thể được sử dụng để chứng minh nhiều đẳng thức toán học phức tạp.
• Tìm giới hạn: Trong một số trường hợp, công thức nhị thức Newton giúp đơn giản hóa biểu thức và tìm giới hạn của các hàm số.

2.2. Vật Lý

• Tính gần đúng: Trong vật lý, công thức nhị thức Newton được sử dụng để tính gần đúng các biểu thức phức tạp khi một số hạng nhỏ hơn rất nhiều so với các số hạng khác. Ví dụ, trong cơ học cổ điển, khi vận tốc của vật nhỏ hơn rất nhiều so với vận tốc ánh sáng, ta có thể sử dụng công thức nhị thức Newton để đơn giản hóa các công thức liên quan đến hiệu ứng tương đối tính.
• Dao động: Trong các bài toán về dao động, công thức nhị thức Newton có thể được sử dụng để phân tích và giải các phương trình dao động phức tạp.

2.3. Khoa Học Máy Tính

• Xây dựng thuật toán: Trong một số thuật toán, công thức nhị thức Newton được sử dụng để tính toán các giá trị tổ hợp, từ đó giải quyết các bài toán liên quan đến tổ hợp và xác suất.
• Phân tích dữ liệu: Trong phân tích dữ liệu, công thức nhị thức Newton có thể được sử dụng để mô hình hóa và phân tích các hiện tượng tuân theo phân phối nhị thức.

2.4. Kinh Tế và Tài Chính

• Mô hình hóa rủi ro: Trong lĩnh vực tài chính, công thức nhị thức Newton có thể được sử dụng để mô hình hóa rủi ro và tính toán giá trị của các công cụ tài chính phức tạp.
• Dự báo: Trong kinh tế, công thức nhị thức Newton có thể được sử dụng để dự báo các xu hướng và biến động của thị trường.

2.5. Thống Kê

• Phân phối nhị thức: Công thức nhị thức Newton là nền tảng của phân phối nhị thức, một phân phối xác suất quan trọng trong thống kê. Phân phối nhị thức được sử dụng để mô hình hóa số lượng thành công trong một chuỗi các thử nghiệm độc lập, mỗi thử nghiệm có hai kết quả có thể xảy ra (thành công hoặc thất bại).
• Kiểm định giả thuyết: Trong kiểm định giả thuyết, công thức nhị thức Newton được sử dụng để tính toán p-value, một thước đo mức độ tin cậy của giả thuyết.

2.6. Ví Dụ Cụ Thể

• Tính lãi kép: Giả sử bạn gửi một khoản tiền vào ngân hàng với lãi suất r mỗi kỳ. Sau n kỳ, số tiền bạn nhận được sẽ là (1 + r)ⁿ lần số tiền ban đầu. Công thức nhị thức Newton có thể được sử dụng để khai triển biểu thức này và tính toán số tiền bạn nhận được sau n kỳ.
• Xác suất trúng xổ số: Giả sử bạn mua một vé xổ số có n số, và bạn cần trúng k số để thắng giải. Xác suất trúng giải có thể được tính bằng công thức nhị thức Newton.
• Phân tích gen: Trong di truyền học, công thức nhị thức Newton được sử dụng để tính toán xác suất xuất hiện của các kiểu gen khác nhau trong quần thể.

3. Các Dạng Bài Tập Thường Gặp và Phương Pháp Giải

Công thức nhị thức Newton là một chủ đề quan trọng trong chương trình toán học phổ thông, và có rất nhiều dạng bài tập khác nhau liên quan đến công thức này. Dưới đây là một số dạng bài tập thường gặp và phương pháp giải:

3.1. Khai Triển Trực Tiếp

Dạng bài: Cho biểu thức (a + b)ⁿ, hãy khai triển biểu thức này bằng công thức nhị thức Newton.

Phương pháp giải:

1. Xác định a, b và n.
2. Áp dụng công thức nhị thức Newton: (a + b)ⁿ = ∑_k=0ⁿ C(n, k) a^n-k b^k.
3. Tính các hệ số C(n, k) bằng công thức tổ hợp hoặc sử dụng tam giác Pascal.
4. Viết khai triển đầy đủ, rút gọn nếu có thể.

Ví dụ: Khai triển biểu thức (2x + y)³.

Giải:

1. a = 2x, b = y, n = 3.
2. (2x + y)³ = C(3, 0) (2x)³ + C(3, 1) (2x)² y + C(3, 2) (2x) y² + C(3, 3) y³.
3. C(3, 0) = 1, C(3, 1) = 3, C(3, 2) = 3, C(3, 3) = 1.
4. (2x + y)³ = 1 (2x)³ + 3 (2x)² y + 3 (2x) y² + 1 y³ = 8x³ + 12x²y + 6xy² + y³.

3.2. Tìm Số Hạng Tổng Quát

Dạng bài: Cho khai triển (a + b)ⁿ, tìm số hạng thứ k+1.

Phương pháp giải:

1. Xác định a, b, n và k.
2. Áp dụng công thức số hạng tổng quát: T_k+1 = C(n, k) a^n-k b^k.
3. Tính C(n, k) và thay vào công thức để tìm số hạng thứ k+1.

Ví dụ: Tìm số hạng thứ 3 trong khai triển (x – 1)⁵.

Giải:

1. a = x, b = -1, n = 5, k = 2 (vì số hạng thứ 3 tương ứng với k = 2).
2. T₃ = C(5, 2) x^5-2 (-1)².
3. C(5, 2) = 10.
4. T₃ = 10 x³ 1 = 10x³.

3.3. Tìm Hệ Số của Một Số Hạng

Dạng bài: Cho khai triển (a + b)ⁿ, tìm hệ số của số hạng chứa x^m.

Phương pháp giải:

1. Viết số hạng tổng quát: T_k+1 = C(n, k) a^n-k b^k.
2. Xác định giá trị của k sao cho số mũ của x trong T_k+1 bằng m.
3. Thay giá trị k vừa tìm được vào công thức T_k+1 để tìm hệ số của số hạng chứa x^m.

Ví dụ: Tìm hệ số của x² trong khai triển (x + 2)⁴.

Giải:

1. T_k+1 = C(4, k) x^4-k 2^k.
2. Ta cần tìm k sao cho 4 – k = 2, suy ra k = 2.
3. Hệ số của x² là C(4, 2) 2² = 6 4 = 24.

3.4. Tìm Số Hạng Không Chứa x

Dạng bài: Cho khai triển (a + b)ⁿ, trong đó a và b là các biểu thức chứa x, tìm số hạng không chứa x (tức là số hạng có số mũ của x bằng 0).

Phương pháp giải:

1. Viết số hạng tổng quát: T_k+1 = C(n, k) a^n-k b^k.
2. Xác định giá trị của k sao cho số mũ của x trong T_k+1 bằng 0.
3. Thay giá trị k vừa tìm được vào công thức T_k+1 để tìm số hạng không chứa x.

Ví dụ: Tìm số hạng không chứa x trong khai triển (x + 1/x)⁶.

Giải:

1. T_k+1 = C(6, k) x^6-k (1/x)^k = C(6, k) * x^6-2k.
2. Ta cần tìm k sao cho 6 – 2k = 0, suy ra k = 3.
3. Số hạng không chứa x là C(6, 3) = 20.

3.5. Tính Tổng Các Hệ Số

Dạng bài: Cho khai triển (a + b)ⁿ = a₀ + a₁x + a₂x² + … + a_nxⁿ, tính tổng a₀ + a₁ + a₂ + … + a_n.

Phương pháp giải:

1. Thay x = 1 vào khai triển: (a + b)ⁿ = a₀ + a₁ + a₂ + … + a_n.
2. Tính giá trị của (a + b)ⁿ.

Ví dụ: Tính tổng các hệ số trong khai triển (1 + x)⁵.

Giải:

1. Thay x = 1 vào khai triển: (1 + 1)⁵ = a₀ + a₁ + a₂ + a₃ + a₄ + a₅.
2. (1 + 1)⁵ = 2⁵ = 32.
3. Vậy tổng các hệ số là 32.

3.6. Tính Tổng Các Hệ Số với Dấu Xen Kẽ

Dạng bài: Cho khai triển (a + b)ⁿ = a₀ + a₁x + a₂x² + … + a_nxⁿ, tính tổng a₀ – a₁ + a₂ – a₃ + … + (-1)ⁿa_n.

Phương pháp giải:

1. Thay x = -1 vào khai triển: (a – b)ⁿ = a₀ – a₁ + a₂ – a₃ + … + (-1)ⁿa_n.
2. Tính giá trị của (a – b)ⁿ.

Ví dụ: Tính tổng các hệ số với dấu xen kẽ trong khai triển (1 + x)⁵.

Giải:

1. Thay x = -1 vào khai triển: (1 – 1)⁵ = a₀ – a₁ + a₂ – a₃ + a₄ – a₅.
2. (1 – 1)⁵ = 0⁵ = 0.
3. Vậy tổng các hệ số với dấu xen kẽ là 0.

3.7. Bài Toán Liên Quan Đến Tổ Hợp

Dạng bài: Các bài toán liên quan đến việc đếm số lượng các tổ hợp, chỉnh hợp, hoặc giải các bài toán xác suất sử dụng công thức nhị thức Newton.

Phương pháp giải:

1. Xác định bài toán thuộc loại tổ hợp hay xác suất.
2. Sử dụng công thức nhị thức Newton để tính toán các giá trị tổ hợp cần thiết.
3. Áp dụng các quy tắc đếm hoặc công thức xác suất để giải bài toán.

Ví dụ: Một lớp học có 20 học sinh. Cần chọn ra 5 học sinh để tham gia đội văn nghệ. Hỏi có bao nhiêu cách chọn?

Giải:

1. Đây là bài toán tổ hợp, vì thứ tự chọn không quan trọng.
2. Số cách chọn 5 học sinh từ 20 học sinh là C(20, 5) = 20! / (5! * 15!) = 15504.
3. Vậy có 15504 cách chọn.

3.8. Bài Toán Chứng Minh Đẳng Thức

Dạng bài: Chứng minh một đẳng thức liên quan đến công thức nhị thức Newton.

Phương pháp giải:

1. Sử dụng công thức nhị thức Newton để khai triển các biểu thức trong đẳng thức.
2. Biến đổi các biểu thức đã khai triển để chứng minh đẳng thức.
3. Sử dụng các tính chất của hệ số nhị thức và các hệ quả của công thức nhị thức Newton để đơn giản hóa quá trình chứng minh.

Ví dụ: Chứng minh rằng C(n, 0) + C(n, 1) + … + C(n, n) = 2ⁿ.

Giải:

1. Áp dụng công thức nhị thức Newton cho (1 + 1)ⁿ: (1 + 1)ⁿ = C(n, 0) + C(n, 1) + … + C(n, n).
2. (1 + 1)ⁿ = 2ⁿ.
3. Vậy C(n, 0) + C(n, 1) + … + C(n, n) = 2ⁿ.

4. Mẹo và Thủ Thuật Khi Sử Dụng Công Thức Nhị Thức Newton

Để sử dụng công thức nhị thức Newton một cách hiệu quả, bạn có thể áp dụng một số mẹo và thủ thuật sau:

• Nhận diện dạng bài: Trước khi bắt đầu giải bài tập, hãy xác định rõ dạng bài để chọn phương pháp giải phù hợp.
• Sử dụng tam giác Pascal: Khi n nhỏ, sử dụng tam giác Pascal để tìm các hệ số nhị thức sẽ nhanh hơn so với việc tính toán bằng công thức tổ hợp.
• Ghi nhớ các hệ quả: Ghi nhớ các hệ quả của công thức nhị thức Newton (ví dụ: tổng các hệ số, tổng các hệ số với dấu xen kẽ) để áp dụng trực tiếp vào bài toán.
• Rút gọn biểu thức: Trước khi khai triển, hãy rút gọn biểu thức (a + b)ⁿ nếu có thể.
• Kiểm tra lại kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả bằng cách thay một vài giá trị cụ thể của x vào biểu thức ban đầu và biểu thức đã khai triển để đảm bảo chúng có giá trị bằng nhau.

5. Lời Khuyên Học Tập và Nguồn Tài Liệu Tham Khảo

Để học tốt công thức nhị thức Newton, bạn nên:

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, công thức, các tính chất và hệ quả của công thức nhị thức Newton.
• Làm nhiều bài tập: Luyện tập giải nhiều bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải toán.
• Tham khảo tài liệu: Đọc thêm sách, báo, và các tài liệu trực tuyến về công thức nhị thức Newton để mở rộng kiến thức và hiểu sâu hơn về chủ đề này.

Một số nguồn tài liệu tham khảo hữu ích:

• Sách giáo khoa toán học lớp 10: Cung cấp kiến thức cơ bản về công thức nhị thức Newton.
• Các trang web học toán trực tuyến: Ví dụ như Khan Academy, VietJack, tic.edu.vn cung cấp các bài giảng, bài tập và tài liệu tham khảo về công thức nhị thức Newton.
• Sách bài tập toán nâng cao: Cung cấp các bài tập khó và phức tạp hơn về công thức nhị thức Newton.

6. Tại Sao Nên Học Công Thức Nhị Thức Newton tại tic.edu.vn?

tic.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng về công thức nhị thức Newton, bao gồm:

• Bài viết chi tiết và dễ hiểu: Các bài viết được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, trình bày kiến thức một cách rõ ràng, dễ hiểu, phù hợp với mọi đối tượng học sinh.
• Ví dụ minh họa đa dạng: Các ví dụ được lựa chọn kỹ lưỡng, bao gồm nhiều dạng bài tập khác nhau, giúp học sinh nắm vững phương pháp giải toán.
• Bài tập tự luyện có đáp án: Các bài tập tự luyện được thiết kế theo nhiều mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải toán và kiểm tra kiến thức.
• Cộng đồng học tập sôi động: Học sinh có thể tham gia vào cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức, thảo luận bài tập và nhận được sự hỗ trợ từ các bạn học và giáo viên.
• Công cụ hỗ trợ học tập hiệu quả: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp học sinh học tập hiệu quả hơn.

Ngoài ra, tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất và chính xác, giúp học sinh nắm bắt được các xu hướng và thay đổi trong chương trình học.

7. Tổng Kết

Công thức nhị thức Newton là một công cụ mạnh mẽ và hữu ích trong toán học và nhiều lĩnh vực khác. Việc nắm vững công thức này sẽ giúp bạn giải quyết nhiều bài toán phức tạp và mở rộng kiến thức của mình. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục công thức nhị thức Newton và đạt được thành công trong học tập.

8. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về công thức nhị thức Newton? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt về công thức nhị thức Newton!

Tại tic.edu.vn, bạn sẽ tìm thấy:

• Các bài viết chi tiết, dễ hiểu về công thức nhị thức Newton.
• Ví dụ minh họa đa dạng, giúp bạn nắm vững phương pháp giải toán.
• Bài tập tự luyện có đáp án, giúp bạn rèn luyện kỹ năng giải toán và kiểm tra kiến thức.
• Cộng đồng học tập sôi động, nơi bạn có thể trao đổi kiến thức, thảo luận bài tập và nhận được sự hỗ trợ từ các bạn học và giáo viên.
• Các công cụ hỗ trợ học tập trực tuyến, giúp bạn học tập hiệu quả hơn.

Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn về công thức nhị thức Newton! Hãy truy cập tic.edu.vn ngay bây giờ!

Email: [email protected]

Trang web: tic.edu.vn

9. Câu Hỏi Thường Gặp (FAQ)

1. Công thức nhị thức Newton là gì?

Công thức nhị thức Newton là một công thức toán học cho phép khai triển một biểu thức có dạng (a + b)ⁿ thành một tổng các số hạng.

2. Công thức nhị thức Newton có dạng như thế nào?

(a + b)ⁿ = ∑_k=0ⁿ C(n, k) a^n-k b^k

3. Các hệ số C(n, k) được tính như thế nào?

C(n, k) = n! / (k! * (n-k)!)

4. Công thức nhị thức Newton có những tính chất quan trọng nào?

• Số lượng số hạng là n + 1.
• Tổng số mũ của a và b trong mỗi số hạng luôn bằng n.
• Các hệ số C(n, k) có tính đối xứng: C(n, k) = C(n, n-k).

5. Số hạng tổng quát trong khai triển (a + b)ⁿ có dạng như thế nào?

T_k+1 = C(n, k) a^n-k b^k

6. Làm thế nào để tìm hệ số của một số hạng cụ thể trong khai triển?

Sử dụng công thức số hạng tổng quát và xác định giá trị của k sao cho số mũ của biến số trong số hạng đó bằng số mũ đã cho.

7. Làm thế nào để tìm số hạng không chứa x trong khai triển?

Sử dụng công thức số hạng tổng quát và xác định giá trị của k sao cho số mũ của x bằng 0.

8. Làm thế nào để tính tổng các hệ số trong khai triển?

Thay x = 1 vào khai triển.

9. Làm thế nào để tính tổng các hệ số với dấu xen kẽ trong khai triển?

Thay x = -1 vào khai triển.

10. tic.edu.vn có thể giúp tôi học công thức nhị thức Newton như thế nào?

tic.edu.vn cung cấp các bài viết chi tiết, ví dụ minh họa, bài tập tự luyện và cộng đồng học tập sôi động để giúp bạn nắm vững công thức nhị thức Newton và giải quyết các bài toán liên quan.