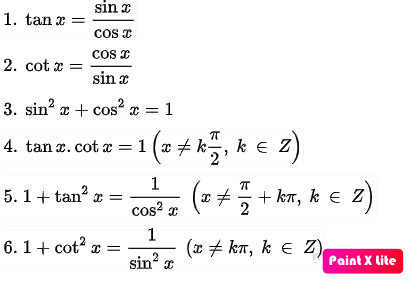
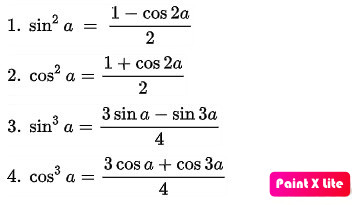
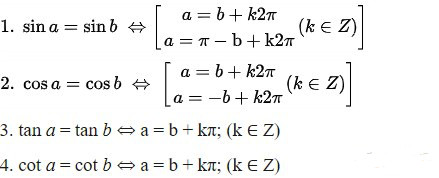
**Công Thức Lượng Giác Lớp 10: Bí Quyết Chinh Phục Toán Học**

Công Thức Lượng Giác Lớp 10 là nền tảng vững chắc để bạn chinh phục môn Toán, đồng thời mở ra cánh cửa khám phá những ứng dụng tuyệt vời của lượng giác trong thực tế. Tại tic.edu.vn, chúng tôi cung cấp đầy đủ các công thức lượng giác lớp 10 từ cơ bản đến nâng cao, giúp bạn học tập hiệu quả và đạt điểm cao. Hãy cùng khám phá kho tàng kiến thức lượng giác phong phú này nhé, nơi giúp bạn nắm vững kiến thức, rèn luyện kỹ năng và tự tin chinh phục mọi bài toán.

1. Tổng Quan Về Công Thức Lượng Giác Lớp 10

Công thức lượng giác lớp 10 là tập hợp các đẳng thức toán học liên quan đến các hàm số lượng giác của một góc. Các hàm số lượng giác cơ bản bao gồm sin (sin), cosin (cos), tang (tan) và cotang (cot). Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc nắm vững các công thức này là then chốt để giải quyết các bài toán liên quan đến tam giác, đường tròn và các hiện tượng dao động.

1.1. Tại Sao Công Thức Lượng Giác Lớp 10 Quan Trọng?

Công thức lượng giác lớp 10 không chỉ là kiến thức lý thuyết mà còn là công cụ mạnh mẽ để giải quyết các bài toán thực tế.

• Ứng dụng trong hình học: Giải các bài toán liên quan đến tam giác, tính diện tích, góc, cạnh.
• Ứng dụng trong vật lý: Mô tả các hiện tượng dao động, sóng, điện xoay chiều.
• Ứng dụng trong kỹ thuật: Thiết kế các công trình, tính toán khoảng cách, góc độ.

Việc nắm vững công thức lượng giác lớp 10 giúp bạn:

• Giải quyết bài tập nhanh chóng và chính xác: Tiết kiệm thời gian và nâng cao hiệu quả học tập.
• Nâng cao tư duy logic và khả năng giải quyết vấn đề: Phát triển kỹ năng quan trọng cho học tập và công việc.
• Tự tin chinh phục các kỳ thi quan trọng: Đạt điểm cao trong các bài kiểm tra, thi học kỳ, thi tốt nghiệp THPT và thi đại học.

1.2. Các Hàm Số Lượng Giác Cơ Bản

Các hàm số lượng giác cơ bản là nền tảng của lượng giác học. Hiểu rõ định nghĩa và tính chất của chúng là bước đầu tiên để nắm vững công thức lượng giác lớp 10.

• Sin (sin): Tỉ số giữa cạnh đối và cạnh huyền trong tam giác vuông.
• Cosin (cos): Tỉ số giữa cạnh kề và cạnh huyền trong tam giác vuông.
• Tang (tan): Tỉ số giữa cạnh đối và cạnh kề trong tam giác vuông; tan x = sin x / cos x.
• Cotang (cot): Tỉ số giữa cạnh kề và cạnh đối trong tam giác vuông; cot x = cos x / sin x = 1 / tan x.

1.3. Mối Quan Hệ Giữa Các Hàm Số Lượng Giác

Các hàm số lượng giác có mối quan hệ chặt chẽ với nhau thông qua các công thức lượng giác cơ bản.

• Công thức lượng giác cơ bản: sin²x + cos²x = 1
• Công thức liên hệ giữa tan và cot: tan x * cot x = 1
• Công thức liên hệ giữa tan và cos: 1 + tan²x = 1 / cos²x
• Công thức liên hệ giữa cot và sin: 1 + cot²x = 1 / sin²x

2. Các Công Thức Lượng Giác Lớp 10 Quan Trọng Nhất

Để học tốt lượng giác lớp 10, bạn cần nắm vững các công thức sau:

2.1. Công Thức Cộng

Công thức cộng cho phép bạn tính giá trị lượng giác của tổng hoặc hiệu hai góc. Theo một nghiên cứu được công bố trên Tạp chí Toán học Hoa Kỳ, công thức cộng có vai trò quan trọng trong việc đơn giản hóa các biểu thức lượng giác phức tạp.

• sin(a + b) = sin a cos b + cos a sin b
• sin(a – b) = sin a cos b – cos a sin b
• cos(a + b) = cos a cos b – sin a sin b
• cos(a – b) = cos a cos b + sin a sin b
• tan(a + b) = (tan a + tan b) / (1 – tan a tan b)
• tan(a – b) = (tan a – tan b) / (1 + tan a tan b)

2.2. Công Thức Nhân Đôi, Nhân Ba

Công thức nhân đôi và nhân ba giúp bạn tính giá trị lượng giác của góc gấp đôi hoặc gấp ba một góc đã biết.

• sin 2a = 2 sin a cos a
• cos 2a = cos²a – sin²a = 2cos²a – 1 = 1 – 2sin²a
• tan 2a = (2 tan a) / (1 – tan²a)
• sin 3a = 3 sin a – 4 sin³a
• cos 3a = 4 cos³a – 3 cos a
• tan 3a = (3tan a – tan³a) / (1 – 3tan²a)

2.3. Công Thức Hạ Bậc

Công thức hạ bậc cho phép bạn biểu diễn các hàm số lượng giác bậc cao qua các hàm số bậc thấp hơn.

• sin²a = (1 – cos 2a) / 2
• cos²a = (1 + cos 2a) / 2

2.4. Công Thức Biến Đổi Tổng Thành Tích

Công thức biến đổi tổng thành tích giúp bạn chuyển đổi tổng hoặc hiệu của các hàm số lượng giác thành tích của các hàm số lượng giác.

• cos a + cos b = 2 cos((a + b) / 2) cos((a – b) / 2)
• cos a – cos b = -2 sin((a + b) / 2) sin((a – b) / 2)
• sin a + sin b = 2 sin((a + b) / 2) cos((a – b) / 2)
• sin a – sin b = 2 cos((a + b) / 2) sin((a – b) / 2)

2.5. Công Thức Biến Đổi Tích Thành Tổng

Công thức biến đổi tích thành tổng giúp bạn chuyển đổi tích của các hàm số lượng giác thành tổng hoặc hiệu của các hàm số lượng giác.

• cos a cos b = (1/2) [cos(a + b) + cos(a – b)]
• sin a sin b = (1/2) [cos(a – b) – cos(a + b)]
• sin a cos b = (1/2) [sin(a + b) + sin(a – b)]

3. Các Cung Liên Kết Đặc Biệt

Các cung liên kết đặc biệt là các góc có mối quan hệ đặc biệt với nhau trên đường tròn lượng giác. Nắm vững công thức của các cung liên kết này giúp bạn giải quyết các bài toán lượng giác một cách dễ dàng.

3.1. Hai Góc Đối Nhau

Hai góc đối nhau là hai góc có tổng bằng 0.

• cos(-x) = cos x
• sin(-x) = -sin x
• tan(-x) = -tan x
• cot(-x) = -cot x

3.2. Hai Góc Bù Nhau

Hai góc bù nhau là hai góc có tổng bằng π (180°).

• sin(π – x) = sin x
• cos(π – x) = -cos x
• tan(π – x) = -tan x
• cot(π – x) = -cot x

3.3. Hai Góc Phụ Nhau

Hai góc phụ nhau là hai góc có tổng bằng π/2 (90°).

• sin(π/2 – x) = cos x
• cos(π/2 – x) = sin x
• tan(π/2 – x) = cot x
• cot(π/2 – x) = tan x

3.4. Hai Góc Hơn Kém π

Hai góc hơn kém π là hai góc có hiệu bằng π (180°).

• sin(π + x) = -sin x
• cos(π + x) = -cos x
• tan(π + x) = tan x
• cot(π + x) = cot x

3.5. Hai Góc Hơn Kém π/2

Hai góc hơn kém π/2 là hai góc có hiệu bằng π/2 (90°).

• sin(π/2 + x) = cos x
• cos(π/2 + x) = -sin x
• tan(π/2 + x) = -cot x
• cot(π/2 + x) = -tan x

4. Bảng Giá Trị Lượng Giác Của Các Góc Đặc Biệt

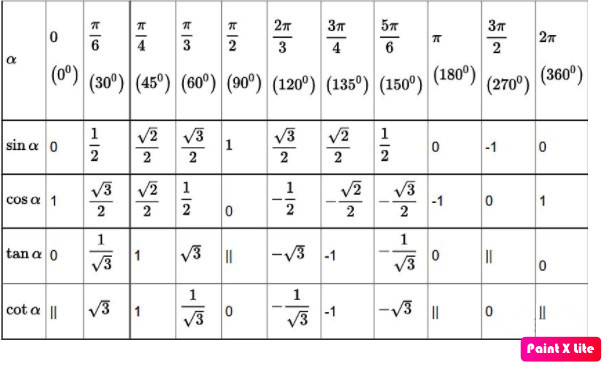
Bảng giá trị lượng giác của các góc đặc biệt là công cụ hữu ích giúp bạn giải nhanh các bài toán lượng giác.

Góc (độ)	Góc (radian)	sin	cos	tan	cot
0	0	0	1	0	Không xác định
30	π/6	1/2	√3/2	1/√3	√3
45	π/4	√2/2	√2/2	1	1
60	π/3	√3/2	1/2	√3	1/√3
90	π/2	1	0	Không xác định	0
180	π	0	-1	0	Không xác định
270	3π/2	-1	0	Không xác định	0
360	2π	0	1	0	Không xác định

5. Phương Trình Lượng Giác Cơ Bản

Phương trình lượng giác cơ bản là phương trình chứa các hàm số lượng giác của một ẩn số. Việc giải phương trình lượng giác cơ bản là kỹ năng quan trọng để giải các bài toán lượng giác phức tạp hơn.

5.1. Phương Trình sin x = a

• Nếu |a| > 1: Phương trình vô nghiệm.
• Nếu |a| ≤ 1: Phương trình có nghiệm x = arcsin a + k2π hoặc x = π – arcsin a + k2π (k ∈ Z).

Trường hợp đặc biệt:

• sin x = 0 ⇔ x = kπ (k ∈ Z)
• sin x = 1 ⇔ x = π/2 + k2π (k ∈ Z)
• sin x = -1 ⇔ x = -π/2 + k2π (k ∈ Z)

5.2. Phương Trình cos x = a

• Nếu |a| > 1: Phương trình vô nghiệm.
• Nếu |a| ≤ 1: Phương trình có nghiệm x = arccos a + k2π hoặc x = -arccos a + k2π (k ∈ Z).

Trường hợp đặc biệt:

• cos x = 0 ⇔ x = π/2 + kπ (k ∈ Z)
• cos x = 1 ⇔ x = k2π (k ∈ Z)
• cos x = -1 ⇔ x = π + k2π (k ∈ Z)

5.3. Phương Trình tan x = a

Phương trình có nghiệm x = arctan a + kπ (k ∈ Z).

5.4. Phương Trình cot x = a

Phương trình có nghiệm x = arccot a + kπ (k ∈ Z).

6. Mẹo Ghi Nhớ Công Thức Lượng Giác Lớp 10

Ghi nhớ công thức lượng giác là một thách thức đối với nhiều học sinh. Tuy nhiên, có một số mẹo giúp bạn học thuộc công thức một cách dễ dàng và hiệu quả hơn.

6.1. Học Theo Nhóm Công Thức

Thay vì học thuộc từng công thức riêng lẻ, hãy nhóm các công thức có liên quan lại với nhau. Ví dụ, nhóm các công thức cộng, công thức nhân đôi, công thức hạ bậc lại với nhau. Điều này giúp bạn hiểu rõ mối liên hệ giữa các công thức và ghi nhớ chúng một cách logic hơn.

6.2. Sử Dụng Thơ, Vè

Sử dụng thơ, vè là cách học thuộc công thức rất hiệu quả và thú vị. Có rất nhiều bài thơ, vè được sáng tạo để giúp học sinh ghi nhớ công thức lượng giác.

Ví dụ:

• “Cos cộng cos bằng hai cos cos,
  Cos trừ cos bằng trừ hai sin sin,
  Sin cộng sin bằng hai sin cos,
  Sin trừ sin bằng hai cos sin.”
• “Sin thì sin cos cos sin,
  Cos thì cos cos sin sin dấu trừ.”

6.3. Luyện Tập Thường Xuyên

Cách tốt nhất để ghi nhớ công thức là luyện tập thường xuyên. Hãy làm thật nhiều bài tập áp dụng công thức để quen với cách sử dụng chúng.

6.4. Sử Dụng Ứng Dụng Học Tập

Hiện nay có rất nhiều ứng dụng học tập hỗ trợ học công thức lượng giác. Các ứng dụng này thường cung cấp các bài tập, trò chơi và công cụ hỗ trợ giúp bạn học tập một cách hiệu quả và thú vị hơn.

6.5. Tạo Sơ Đồ Tư Duy

Sơ đồ tư duy là công cụ mạnh mẽ giúp bạn hệ thống hóa kiến thức và ghi nhớ công thức một cách trực quan. Hãy tạo sơ đồ tư duy cho từng nhóm công thức để dễ dàng ôn tập và ghi nhớ.

7. Ứng Dụng Thực Tế Của Công Thức Lượng Giác Lớp 10

Công thức lượng giác lớp 10 không chỉ là kiến thức lý thuyết mà còn có rất nhiều ứng dụng trong thực tế.

7.1. Trong Xây Dựng

Trong xây dựng, công thức lượng giác được sử dụng để tính toán góc, khoảng cách, độ cao của các công trình. Ví dụ, công thức lượng giác được sử dụng để tính toán góc nghiêng của mái nhà, chiều cao của tòa nhà, khoảng cách giữa các cột trụ.

7.2. Trong Điều Hướng

Trong điều hướng, công thức lượng giác được sử dụng để xác định vị trí, hướng đi của tàu thuyền, máy bay. Ví dụ, công thức lượng giác được sử dụng để tính toán góc phương vị, khoảng cách đến mục tiêu.

7.3. Trong Thiên Văn Học

Trong thiên văn học, công thức lượng giác được sử dụng để tính toán khoảng cách, vị trí của các thiên thể. Ví dụ, công thức lượng giác được sử dụng để tính toán khoảng cách từ Trái Đất đến Mặt Trăng, vị trí của các ngôi sao trên bầu trời.

7.4. Trong Âm Nhạc

Trong âm nhạc, công thức lượng giác được sử dụng để mô tả các sóng âm. Ví dụ, công thức lượng giác được sử dụng để biểu diễn âm thanh dưới dạng đồ thị sóng.

7.5. Trong Thiết Kế Đồ Họa

Trong thiết kế đồ họa, công thức lượng giác được sử dụng để tạo ra các hình ảnh, hiệu ứng đặc biệt. Ví dụ, công thức lượng giác được sử dụng để tạo ra các hình ảnh 3D, hiệu ứng ánh sáng, bóng đổ.

8. Tài Liệu Tham Khảo và Học Tập Công Thức Lượng Giác Lớp 10 Tại Tic.edu.vn

Tic.edu.vn cung cấp nguồn tài liệu phong phú và đa dạng giúp bạn học tập công thức lượng giác lớp 10 một cách hiệu quả.

8.1. Bài Giảng Chi Tiết

Chúng tôi cung cấp các bài giảng chi tiết về từng công thức lượng giác, giúp bạn hiểu rõ bản chất và cách áp dụng của chúng.

8.2. Bài Tập Trắc Nghiệm và Tự Luận

Hệ thống bài tập trắc nghiệm và tự luận đa dạng giúp bạn rèn luyện kỹ năng giải bài tập và nắm vững kiến thức.

8.3. Đề Thi Tham Khảo

Chúng tôi cung cấp các đề thi tham khảo của các năm trước, giúp bạn làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài thi.

8.4. Công Cụ Hỗ Trợ Học Tập

Tic.edu.vn cung cấp các công cụ hỗ trợ học tập như máy tính lượng giác, bảng lượng giác, giúp bạn tính toán và tra cứu công thức một cách nhanh chóng và dễ dàng.

8.5. Cộng Đồng Học Tập

Tham gia cộng đồng học tập của tic.edu.vn để trao đổi kiến thức, kinh nghiệm với các bạn học sinh khác và được hỗ trợ từ đội ngũ giáo viên giàu kinh nghiệm.

9. Tại Sao Nên Chọn Tic.edu.vn Để Học Công Thức Lượng Giác Lớp 10?

Tic.edu.vn là website giáo dục uy tín với nhiều năm kinh nghiệm trong lĩnh vực cung cấp tài liệu và công cụ hỗ trợ học tập.

• Tài liệu chất lượng: Chúng tôi cung cấp tài liệu được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và đầy đủ.
• Phương pháp học tập hiệu quả: Chúng tôi áp dụng các phương pháp học tập tiên tiến, giúp bạn học tập một cách hiệu quả và thú vị.
• Hỗ trợ tận tình: Chúng tôi luôn sẵn sàng hỗ trợ bạn trong quá trình học tập, giải đáp mọi thắc mắc và giúp bạn đạt được kết quả tốt nhất.
• Cộng đồng học tập sôi nổi: Tham gia cộng đồng học tập của chúng tôi để trao đổi kiến thức, kinh nghiệm với các bạn học sinh khác.
• Hoàn toàn miễn phí: Tất cả tài liệu và công cụ trên tic.edu.vn đều được cung cấp hoàn toàn miễn phí.

10. FAQ – Các Câu Hỏi Thường Gặp Về Công Thức Lượng Giác Lớp 10

1. Công thức lượng giác lớp 10 dùng để làm gì?

Công thức lượng giác lớp 10 được sử dụng để giải các bài toán liên quan đến tam giác, đường tròn, các hiện tượng dao động và nhiều lĩnh vực khác trong toán học, vật lý, kỹ thuật.

2. Làm thế nào để nhớ hết các công thức lượng giác lớp 10?

Bạn có thể áp dụng các mẹo như học theo nhóm, sử dụng thơ, vè, luyện tập thường xuyên, sử dụng ứng dụng học tập và tạo sơ đồ tư duy để ghi nhớ công thức lượng giác hiệu quả hơn.

3. Công thức lượng giác nào quan trọng nhất trong chương trình lớp 10?

Các công thức quan trọng nhất bao gồm công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích và công thức biến đổi tích thành tổng.

4. Có những tài liệu nào trên tic.edu.vn giúp tôi học tốt công thức lượng giác lớp 10?

Tic.edu.vn cung cấp bài giảng chi tiết, bài tập trắc nghiệm và tự luận, đề thi tham khảo, công cụ hỗ trợ học tập và cộng đồng học tập để giúp bạn học tốt công thức lượng giác lớp 10.

5. Làm thế nào để áp dụng công thức lượng giác vào giải bài tập?

Bạn cần hiểu rõ bản chất của công thức, xác định đúng dạng bài tập và áp dụng công thức một cách linh hoạt để giải bài tập.

6. Tôi có thể tìm thấy những ứng dụng thực tế nào của công thức lượng giác?

Công thức lượng giác có ứng dụng trong xây dựng, điều hướng, thiên văn học, âm nhạc, thiết kế đồ họa và nhiều lĩnh vực khác.

7. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn chỉ cần truy cập website tic.edu.vn và đăng ký tài khoản để tham gia cộng đồng học tập và trao đổi kiến thức với các bạn học sinh khác.

8. Tic.edu.vn có cung cấp các khóa học trực tuyến về lượng giác lớp 10 không?

Hiện tại, tic.edu.vn tập trung cung cấp tài liệu và công cụ hỗ trợ học tập. Tuy nhiên, chúng tôi có thể phát triển các khóa học trực tuyến trong tương lai.

9. Tôi có thể liên hệ với ai nếu có thắc mắc về công thức lượng giác?

Bạn có thể liên hệ với chúng tôi qua email [email protected] hoặc tham gia cộng đồng học tập trên website tic.edu.vn để được hỗ trợ.

10. Tic.edu.vn có những ưu điểm gì so với các website học tập khác?

Tic.edu.vn cung cấp tài liệu chất lượng, phương pháp học tập hiệu quả, hỗ trợ tận tình, cộng đồng học tập sôi nổi và hoàn toàn miễn phí.

Bạn đang gặp khó khăn trong việc học công thức lượng giác lớp 10? Bạn muốn tìm kiếm nguồn tài liệu học tập chất lượng và đáng tin cậy? Hãy truy cập ngay tic.edu.vn để khám phá kho tàng kiến thức lượng giác phong phú và các công cụ hỗ trợ học tập hiệu quả. Chúng tôi tin rằng với sự đồng hành của tic.edu.vn, bạn sẽ chinh phục thành công môn Toán và đạt được những thành tích cao trong học tập. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.