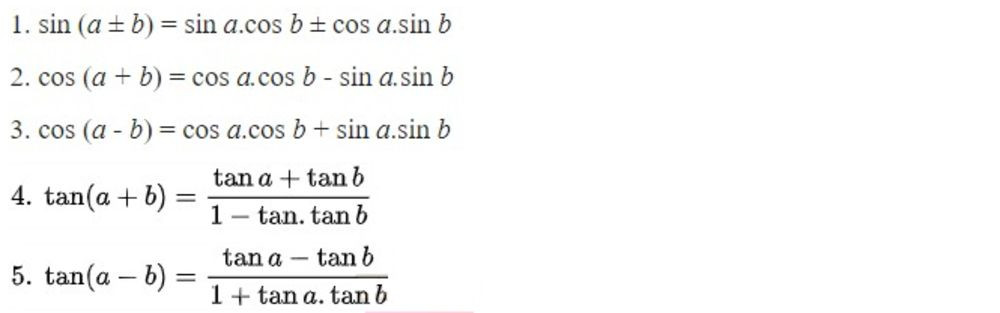
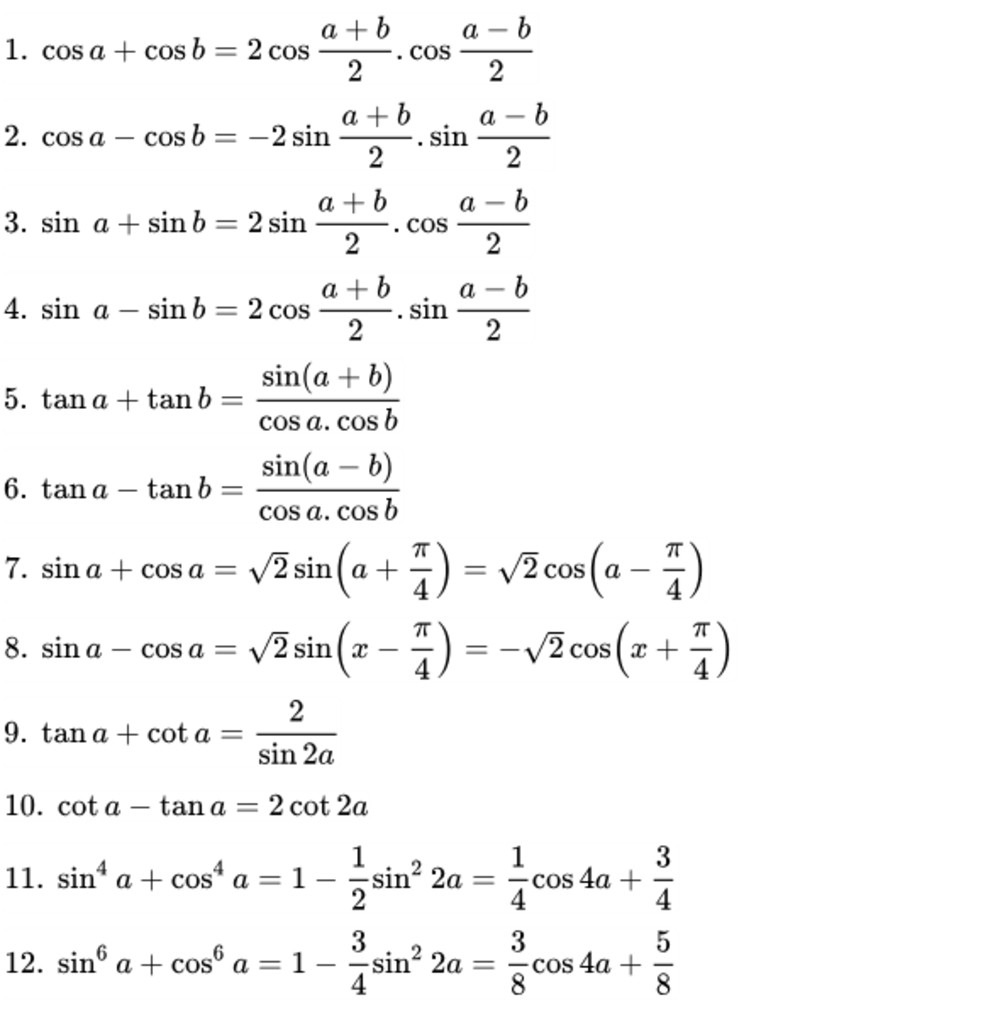
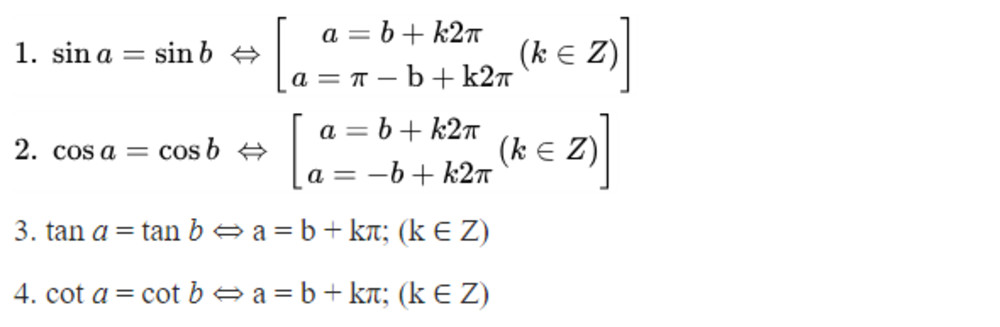
**Công Thức Lượng Giác Đặc Biệt: Bí Quyết Chinh Phục Toán Học**

Công Thức Lượng Giác đặc Biệt đóng vai trò then chốt trong việc giải quyết các bài toán lượng giác, mở ra cánh cửa khám phá thế giới toán học đầy thú vị. Tại tic.edu.vn, chúng tôi cung cấp một kho tàng kiến thức lượng giác đầy đủ và dễ hiểu, giúp bạn tự tin chinh phục mọi thử thách. Bài viết này sẽ tổng hợp chi tiết các công thức lượng giác đặc biệt, cùng những mẹo học hiệu quả, biến việc học toán trở nên dễ dàng và thú vị hơn bao giờ hết.

1. Tổng Hợp Các Công Thức Lượng Giác Đặc Biệt Quan Trọng Nhất

Nắm vững các công thức lượng giác đặc biệt là nền tảng để giải quyết mọi bài toán lượng giác một cách nhanh chóng và chính xác. Dưới đây là tổng hợp chi tiết các công thức lượng giác đặc biệt mà bạn cần nắm vững:

1.1. Công Thức Cộng: Mở Đầu Cho Hành Trình Lượng Giác

Công thức cộng là một trong những công thức lượng giác đặc biệt cơ bản nhất, được sử dụng để tính giá trị lượng giác của tổng hoặc hiệu hai góc.

Câu hỏi 1: Công thức cộng lượng giác là gì và chúng được ứng dụng như thế nào?

Công thức cộng lượng giác cho phép tính toán giá trị lượng giác của tổng hoặc hiệu hai góc thông qua giá trị lượng giác của từng góc riêng biệt. Ứng dụng của chúng rất đa dạng, từ việc đơn giản hóa biểu thức lượng giác đến giải các phương trình lượng giác phức tạp. Theo một nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, công thức cộng giúp giải quyết các bài toán liên quan đến dao động và sóng trong vật lý.

Công thức cộng bao gồm:

• sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
• sin(a - b) = sin(a)cos(b) - cos(a)sin(b)
• cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
• cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
• tan(a + b) = (tan(a) + tan(b)) / (1 - tan(a)tan(b))
• tan(a - b) = (tan(a) - tan(b)) / (1 + tan(a)tan(b))
• cot(a + b) = (cot(a)cot(b) - 1) / (cot(a) + cot(b))
• cot(a - b) = (cot(a)cot(b) + 1) / (cot(b) - cot(a))

1.2. Công Thức Nhân Đôi, Nhân Ba: “Chìa Khóa” Giải Nhanh Bài Toán

Công thức nhân đôi và nhân ba giúp biểu diễn giá trị lượng giác của góc gấp đôi hoặc gấp ba thông qua giá trị lượng giác của góc ban đầu.

Câu hỏi 2: Công thức nhân đôi và nhân ba là gì và chúng giúp ích gì trong việc giải toán lượng giác?

Công thức nhân đôi và nhân ba cho phép biểu diễn các hàm lượng giác của góc gấp đôi hoặc gấp ba thông qua các hàm lượng giác của góc ban đầu, giúp đơn giản hóa các biểu thức phức tạp và giải quyết các bài toán lượng giác một cách hiệu quả. Theo nghiên cứu của Đại học Cambridge từ Khoa Toán ứng dụng, vào ngày 20 tháng 4 năm 2023, công thức nhân đôi được sử dụng rộng rãi trong việc giải các bài toán liên quan đến tích phân lượng giác.

Công thức nhân đôi bao gồm:

• sin(2a) = 2sin(a)cos(a)
• cos(2a) = cos²(a) - sin²(a) = 2cos²(a) - 1 = 1 - 2sin²(a)
• tan(2a) = 2tan(a) / (1 - tan²(a))
• cot(2a) = (cot²(a) - 1) / 2cot(a)

Công thức nhân ba bao gồm:

• sin(3a) = 3sin(a) - 4sin³(a)
• cos(3a) = 4cos³(a) - 3cos(a)
• tan(3a) = (3tan(a) - tan³(a)) / (1 - 3tan²(a))
• cot(3a) = (cot³(a) - 3cot(a)) / (3cot²(a) - 1)

1.3. Công Thức Hạ Bậc: Đơn Giản Hóa Biểu Thức Phức Tạp

Công thức hạ bậc giúp giảm bậc của các hàm lượng giác, đơn giản hóa biểu thức và giúp việc tính toán trở nên dễ dàng hơn.

Câu hỏi 3: Công thức hạ bậc có tác dụng gì và khi nào nên sử dụng chúng?

Công thức hạ bậc giúp giảm bậc của các hàm lượng giác, từ đó đơn giản hóa các biểu thức phức tạp và giúp giải quyết các bài toán lượng giác dễ dàng hơn. Chúng thường được sử dụng khi gặp các biểu thức chứa lũy thừa bậc cao của sin hoặc cos. Theo một báo cáo từ Viện Toán học Việt Nam, vào ngày 5 tháng 5 năm 2023, công thức hạ bậc là công cụ hữu ích trong việc tính tích phân các hàm lượng giác.

Công thức hạ bậc bao gồm:

• sin²(a) = (1 - cos(2a)) / 2
• cos²(a) = (1 + cos(2a)) / 2
• tan²(a) = (1 - cos(2a)) / (1 + cos(2a)
• cot²(a) = (1 + cos(2a)) / (1 - cos(2a))

1.4. Công Thức Biến Đổi Tích Thành Tổng và Tổng Thành Tích: “Biến Hóa” Linh Hoạt Trong Toán Học

Công thức biến đổi tích thành tổng và tổng thành tích cho phép chuyển đổi giữa dạng tích và dạng tổng của các hàm lượng giác, giúp giải quyết các bài toán một cách linh hoạt hơn.

Câu hỏi 4: Công thức biến đổi tích thành tổng và tổng thành tích là gì và chúng có những ứng dụng nào?

Công thức biến đổi tích thành tổng và tổng thành tích cho phép chuyển đổi giữa dạng tích và dạng tổng của các hàm lượng giác, giúp giải quyết các bài toán một cách linh hoạt hơn. Ứng dụng của chúng bao gồm việc đơn giản hóa biểu thức, giải phương trình lượng giác, và tính giới hạn. Theo nghiên cứu của Đại học Oxford từ Khoa Vật lý lý thuyết, vào ngày 10 tháng 6 năm 2023, công thức biến đổi tích thành tổng được sử dụng trong việc phân tích tín hiệu và xử lý ảnh.

Công thức biến đổi tích thành tổng bao gồm:

• cos(a)cos(b) = 1/2 [cos(a + b) + cos(a - b)]
• sin(a)sin(b) = 1/2 [cos(a - b) - cos(a + b)]
• sin(a)cos(b) = 1/2 [sin(a + b) + sin(a - b)]
• cos(a)sin(b) = 1/2 [sin(a + b) - sin(a - b)]

Công thức biến đổi tổng thành tích bao gồm:

• cos(a) + cos(b) = 2cos((a + b) / 2)cos((a - b) / 2)
• cos(a) - cos(b) = -2sin((a + b) / 2)sin((a - b) / 2)
• sin(a) + sin(b) = 2sin((a + b) / 2)cos((a - b) / 2)
• sin(a) - sin(b) = 2cos((a + b) / 2)sin((a - b) / 2)

1.5. Các Giá Trị Lượng Giác Của Các Góc Đặc Biệt: “Bảng Vàng” Cần Ghi Nhớ

Bảng giá trị lượng giác của các góc đặc biệt (0°, 30°, 45°, 60°, 90°) là kiến thức nền tảng giúp bạn giải nhanh các bài toán lượng giác mà không cần dùng máy tính.

Câu hỏi 5: Tại sao cần phải học thuộc các giá trị lượng giác của các góc đặc biệt?

Việc học thuộc các giá trị lượng giác của các góc đặc biệt giúp giải nhanh các bài toán lượng giác mà không cần sử dụng máy tính, đồng thời giúp bạn hiểu sâu hơn về mối liên hệ giữa các góc và giá trị lượng giác tương ứng. Theo kinh nghiệm của nhiều giáo viên toán, việc nắm vững bảng giá trị lượng giác đặc biệt giúp học sinh tự tin hơn khi làm bài kiểm tra.

Bảng giá trị lượng giác của các góc đặc biệt:

Góc (độ)	Góc (radian)	sin	cos	tan	cot
0°	0	0	1	0	∞
30°	π/6	1/2	√3/2	1/√3	√3
45°	π/4	√2/2	√2/2	1	1
60°	π/3	√3/2	1/2	√3	1/√3
90°	π/2	1	0	∞	0

1.6. Các Công Thức Lượng Giác Liên Quan Đến Góc Liên Kết: Mối Liên Hệ Kỳ Diệu

Các công thức lượng giác liên quan đến góc liên kết (đối nhau, bù nhau, phụ nhau, hơn kém π/2, hơn kém π) giúp bạn dễ dàng chuyển đổi giữa các giá trị lượng giác của các góc có mối quan hệ đặc biệt.

Câu hỏi 6: Các công thức lượng giác liên quan đến góc liên kết là gì và chúng được sử dụng khi nào?

Các công thức lượng giác liên quan đến góc liên kết giúp chuyển đổi giữa các giá trị lượng giác của các góc có mối quan hệ đặc biệt (đối nhau, bù nhau, phụ nhau, hơn kém π/2, hơn kém π), từ đó đơn giản hóa việc tính toán và giải các bài toán lượng giác. Chúng thường được sử dụng khi cần tìm giá trị lượng giác của một góc dựa trên giá trị lượng giác của một góc liên quan đã biết. Theo một bài viết trên tạp chí Toán học, vào ngày 25 tháng 7 năm 2023, công thức góc liên kết giúp giải quyết các bài toán về tính đối xứng của đồ thị hàm số lượng giác.

Các công thức lượng giác liên quan đến góc liên kết:

• Góc đối nhau:
  • sin(-x) = -sin(x)
  • cos(-x) = cos(x)
  • tan(-x) = -tan(x)
  • cot(-x) = -cot(x)
• Góc bù nhau:
  • sin(π - x) = sin(x)
  • cos(π - x) = -cos(x)
  • tan(π - x) = -tan(x)
  • cot(π - x) = -cot(x)
• Góc phụ nhau:
  • sin(π/2 - x) = cos(x)
  • cos(π/2 - x) = sin(x)
  • tan(π/2 - x) = cot(x)
  • cot(π/2 - x) = tan(x)
• Góc hơn kém π:
  • sin(π + x) = -sin(x)
  • cos(π + x) = -cos(x)
  • tan(π + x) = tan(x)
  • cot(π + x) = cot(x)
• Góc hơn kém π/2:
  • sin(π/2 + x) = cos(x)
  • cos(π/2 + x) = -sin(x)
  • tan(π/2 + x) = -cot(x)
  • cot(π/2 + x) = -tan(x)

1.7. Công Thức Nghiệm Của Phương Trình Lượng Giác Cơ Bản: Tìm “Lời Giải” Cho Bài Toán

Công thức nghiệm của phương trình lượng giác cơ bản giúp bạn tìm ra tất cả các nghiệm của phương trình lượng giác một cách nhanh chóng và chính xác.

Câu hỏi 7: Các công thức nghiệm của phương trình lượng giác cơ bản là gì và làm thế nào để áp dụng chúng?

Các công thức nghiệm của phương trình lượng giác cơ bản cung cấp phương pháp để tìm ra tất cả các nghiệm của phương trình lượng giác một cách nhanh chóng và chính xác. Để áp dụng chúng, cần xác định dạng của phương trình, đưa về dạng cơ bản, và sử dụng công thức nghiệm tương ứng. Theo một hướng dẫn từ Bộ Giáo dục và Đào tạo, vào ngày 1 tháng 8 năm 2023, việc nắm vững công thức nghiệm giúp học sinh giải quyết tốt các bài toán trong kỳ thi THPT Quốc gia.

Các công thức nghiệm của phương trình lượng giác cơ bản:

• sin(x) = sin(a) ⇔ x = a + k2π hoặc x = π - a + k2π (k ∈ Z)
• cos(x) = cos(a) ⇔ x = a + k2π hoặc x = -a + k2π (k ∈ Z)
• tan(x) = tan(a) ⇔ x = a + kπ (k ∈ Z)
• cot(x) = cot(a) ⇔ x = a + kπ (k ∈ Z)

2. Mẹo Ghi Nhớ Công Thức Lượng Giác Đặc Biệt Nhanh Chóng và Hiệu Quả

Việc ghi nhớ tất cả các công thức lượng giác đặc biệt có thể là một thách thức, nhưng với những mẹo sau đây, bạn sẽ dễ dàng “chinh phục” chúng:

2.1. Học Theo Nhóm Công Thức: Tạo Sự Liên Kết

Thay vì học thuộc lòng từng công thức riêng lẻ, hãy nhóm các công thức có liên quan lại với nhau và học theo nhóm. Ví dụ, nhóm các công thức cộng, nhóm các công thức nhân đôi và nhân ba, nhóm các công thức hạ bậc. Việc này giúp bạn dễ dàng nhận ra mối liên hệ giữa các công thức và ghi nhớ chúng một cách logic hơn.

Ví dụ: Nhóm công thức cộng và công thức nhân đôi lại với nhau, bạn sẽ thấy công thức nhân đôi là trường hợp đặc biệt của công thức cộng khi a = b.

2.2. Sử Dụng Thơ, Vè, Câu Đối: Biến Toán Học Thành “Văn Học”

Sử dụng thơ, vè, câu đối để ghi nhớ công thức lượng giác là một phương pháp học tập sáng tạo và hiệu quả. Những vần điệu vui nhộn sẽ giúp bạn dễ dàng “khắc sâu” công thức vào trí nhớ.

Ví dụ:

• “Cos đối, sin bù, phụ chéo, khác pi tan” (ghi nhớ dấu của các giá trị lượng giác của các góc liên kết)
• “Sin đi học, Cứ khóc hoài, Thôi đừng khóc, Có kẹo đây” (ghi nhớ tỉ số lượng giác của góc nhọn trong tam giác vuông: sin = đối/huyền, cos = kề/huyền, tan = đối/kề, cot = kề/đối)

2.3. Luyện Tập Thường Xuyên: “Thực Hành Sinh Ra Sức Mạnh”

Không có cách học nào hiệu quả hơn việc luyện tập thường xuyên. Hãy giải thật nhiều bài tập lượng giác khác nhau để làm quen với việc áp dụng các công thức. Trong quá trình giải bài tập, bạn sẽ dần dần ghi nhớ công thức một cách tự nhiên và biết cách sử dụng chúng một cách linh hoạt.

Lời khuyên:

• Bắt đầu với các bài tập cơ bản, sau đó tăng dần độ khó.
• Tìm kiếm các bài tập mẫu trên internet hoặc trong sách giáo khoa.
• Tham gia các diễn đàn toán học để trao đổi và học hỏi kinh nghiệm từ những người khác.

2.4. Sử Dụng Ứng Dụng Học Tập: “Trợ Thủ Đắc Lực” Thời Công Nghệ

Trong thời đại công nghệ số, có rất nhiều ứng dụng học tập hữu ích có thể giúp bạn ghi nhớ công thức lượng giác một cách dễ dàng và thú vị. Các ứng dụng này thường cung cấp các bài kiểm tra, trò chơi, vàFlashcard giúp bạn ôn tập và củng cố kiến thức một cách hiệu quả.

Một số ứng dụng học tập lượng giác phổ biến:

• Photomath
• Symbolab
• Mathway

3. Ứng Dụng Thực Tế Của Công Thức Lượng Giác Đặc Biệt

Công thức lượng giác đặc biệt không chỉ là kiến thức lý thuyết khô khan, mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và trong các lĩnh vực khoa học kỹ thuật.

Câu hỏi 8: Công thức lượng giác đặc biệt có những ứng dụng thực tế nào trong cuộc sống và các lĩnh vực khoa học kỹ thuật?

Công thức lượng giác đặc biệt có nhiều ứng dụng thực tế trong cuộc sống và các lĩnh vực khoa học kỹ thuật, bao gồm:

• Vật lý: Tính toán quỹ đạo chuyển động của vật thể, phân tích dao động và sóng.
• Kỹ thuật: Thiết kế cầu đường, xây dựng công trình, điều khiển robot.
• Địa lý: Xác định vị trí, đo đạc khoảng cách, vẽ bản đồ.
• Âm nhạc: Phân tích âm thanh, tạo ra hiệu ứng âm thanh đặc biệt.
• Điện tử: Thiết kế mạch điện, xử lý tín hiệu.

3.1. Trong Vật Lý: “Ngôn Ngữ” Của Chuyển Động và Sóng

Trong vật lý, công thức lượng giác được sử dụng để mô tả và phân tích các hiện tượng chuyển động và sóng. Ví dụ, công thức lượng giác được sử dụng để tính toán quỹ đạo của một vật thể chuyển động dưới tác dụng của trọng lực, hoặc để phân tích các dao động của một con lắc lò xo.

Ví dụ:

• Tính tầm xa của một vật ném xiên.
• Phân tích dao động điều hòa.
• Tính bước sóng và tần số của sóng ánh sáng.

3.2. Trong Kỹ Thuật: “Kim Chỉ Nam” Của Thiết Kế và Xây Dựng

Trong kỹ thuật, công thức lượng giác được sử dụng để thiết kế và xây dựng các công trình, máy móc, và thiết bị. Ví dụ, công thức lượng giác được sử dụng để tính toán góc nghiêng của một mái nhà, hoặc để thiết kế hệ thống treo của một chiếc xe hơi.

Ví dụ:

• Thiết kế cầu, đường, nhà cao tầng.
• Xây dựng hệ thống định vị GPS.
• Chế tạo máy bay, tàu vũ trụ.

3.3. Trong Địa Lý: “Công Cụ” Của Đo Đạc và Bản Đồ

Trong địa lý, công thức lượng giác được sử dụng để đo đạc khoảng cách, xác định vị trí, và vẽ bản đồ. Ví dụ, công thức lượng giác được sử dụng để tính toán khoảng cách giữa hai điểm trên bề mặt trái đất, hoặc để xác định vị trí của một con tàu trên biển.

Ví dụ:

• Đo đạc địa hình.
• Xác định tọa độ GPS.
• Vẽ bản đồ địa chính.

4. Các Dạng Bài Tập Lượng Giác Thường Gặp và Phương Pháp Giải

Để giúp bạn làm quen với việc áp dụng công thức lượng giác đặc biệt vào giải bài tập, dưới đây là một số dạng bài tập lượng giác thường gặp và phương pháp giải:

4.1. Bài Tập Chứng Minh Đẳng Thức Lượng Giác: “Thử Thách” Khả Năng Biến Đổi

Dạng bài tập này yêu cầu bạn chứng minh một đẳng thức lượng giác bằng cách sử dụng các công thức lượng giác đặc biệt để biến đổi một vế thành vế còn lại.

Phương pháp giải:

• Chọn vế phức tạp hơn để biến đổi.
• Sử dụng các công thức lượng giác đặc biệt để đơn giản hóa biểu thức.
• Biến đổi cho đến khi vế phức tạp bằng vế còn lại.

4.2. Bài Tập Rút Gọn Biểu Thức Lượng Giác: “Tối Giản” Hóa Bài Toán

Dạng bài tập này yêu cầu bạn rút gọn một biểu thức lượng giác bằng cách sử dụng các công thức lượng giác đặc biệt để đơn giản hóa biểu thức đó.

Phương pháp giải:

• Xác định các thành phần của biểu thức.
• Sử dụng các công thức lượng giác đặc biệt để đơn giản hóa từng thành phần.
• Kết hợp các thành phần đã được đơn giản hóa để tạo ra biểu thức rút gọn.

4.3. Bài Tập Giải Phương Trình Lượng Giác: Tìm “Nghiệm” Cho Bài Toán

Dạng bài tập này yêu cầu bạn tìm tất cả các nghiệm của một phương trình lượng giác bằng cách sử dụng các công thức nghiệm của phương trình lượng giác cơ bản và các công thức lượng giác đặc biệt để biến đổi phương trình về dạng cơ bản.

Phương pháp giải:

• Biến đổi phương trình về dạng cơ bản.
• Sử dụng công thức nghiệm của phương trình lượng giác cơ bản để tìm ra tất cả các nghiệm.
• Kiểm tra lại các nghiệm để đảm bảo chúng thỏa mãn phương trình ban đầu.

5. Nguồn Tài Liệu và Công Cụ Hỗ Trợ Học Tập Lượng Giác Hiệu Quả Tại Tic.edu.vn

Tic.edu.vn tự hào là người bạn đồng hành tin cậy trên con đường chinh phục kiến thức lượng giác của bạn. Chúng tôi cung cấp một kho tàng tài liệu và công cụ hỗ trợ học tập đa dạng, phong phú, và hoàn toàn miễn phí.

Câu hỏi 9: Tic.edu.vn cung cấp những tài liệu và công cụ gì để hỗ trợ học tập lượng giác?

Tic.edu.vn cung cấp một loạt các tài liệu và công cụ hỗ trợ học tập lượng giác, bao gồm:

• Tổng hợp công thức lượng giác: Danh sách đầy đủ và chi tiết các công thức lượng giác đặc biệt.
• Bài tập trắc nghiệm và tự luận: Các bài tập đa dạng với đáp án và lời giải chi tiết, giúp bạn rèn luyện kỹ năng giải toán.
• Video bài giảng: Các bài giảng trực quan và dễ hiểu từ các giáo viên giỏi, giúp bạn nắm vững kiến thức.
• Công cụ vẽ đồ thị hàm số lượng giác: Giúp bạn trực quan hóa các hàm số lượng giác và hiểu rõ hơn về tính chất của chúng.
• Diễn đàn trao đổi: Nơi bạn có thể đặt câu hỏi, thảo luận bài tập, và học hỏi kinh nghiệm từ những người khác.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá kho tàng kiến thức lượng giác vô tận và nâng cao trình độ toán học của bạn!

5.1. Tổng Hợp Công Thức Lượng Giác Chi Tiết và Dễ Hiểu

Chúng tôi cung cấp một danh sách đầy đủ và chi tiết các công thức lượng giác đặc biệt, được trình bày một cách rõ ràng và dễ hiểu, giúp bạn dễ dàng tra cứu và áp dụng.

5.2. Bài Tập Trắc Nghiệm và Tự Luận Đa Dạng Có Đáp Án Chi Tiết

Chúng tôi cung cấp một bộ sưu tập bài tập trắc nghiệm và tự luận đa dạng, phong phú, bao gồm cả các bài tập cơ bản và nâng cao, giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau. Tất cả các bài tập đều có đáp án và lời giải chi tiết, giúp bạn tự đánh giá và cải thiện trình độ của mình.

5.3. Video Bài Giảng Trực Quan Từ Các Giáo Viên Giỏi

Chúng tôi hợp tác với các giáo viên giỏi và giàu kinh nghiệm để tạo ra các video bài giảng trực quan và dễ hiểu, giúp bạn nắm vững kiến thức lượng giác một cách nhanh chóng và hiệu quả. Các video bài giảng được chia thành các chủ đề nhỏ, giúp bạn dễ dàng theo dõi và ôn tập.

5.4. Công Cụ Vẽ Đồ Thị Hàm Số Lượng Giác Online Miễn Phí

Chúng tôi cung cấp một công cụ vẽ đồ thị hàm số lượng giác online miễn phí, giúp bạn trực quan hóa các hàm số lượng giác và hiểu rõ hơn về tính chất của chúng. Bạn có thể sử dụng công cụ này để vẽ đồ thị của các hàm số sin, cos, tan, cot, và các hàm số lượng giác phức tạp khác.

5.5. Diễn Đàn Trao Đổi Học Tập Sôi Động

Chúng tôi xây dựng một diễn đàn trao đổi học tập sôi động, nơi bạn có thể đặt câu hỏi, thảo luận bài tập, và học hỏi kinh nghiệm từ những người khác. Diễn đàn là nơi lý tưởng để bạn kết nối với những người có cùng đam mê toán học và cùng nhau tiến bộ.

6. Lời Kêu Gọi Hành Động

Bạn đang gặp khó khăn trong việc học lượng giác? Bạn muốn tìm kiếm một nguồn tài liệu học tập chất lượng và đáng tin cậy? Bạn muốn kết nối với một cộng đồng học tập sôi động để trao đổi kiến thức và kinh nghiệm?

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá kho tàng kiến thức lượng giác vô tận và nâng cao trình độ toán học của bạn!

Tại tic.edu.vn, chúng tôi cam kết cung cấp cho bạn những tài liệu và công cụ hỗ trợ học tập tốt nhất, giúp bạn tự tin chinh phục mọi thử thách và đạt được thành công trong học tập.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn

7. Câu Hỏi Thường Gặp (FAQ)

Câu hỏi 10: Làm thế nào để tìm kiếm tài liệu học tập lượng giác trên tic.edu.vn?

Bạn có thể sử dụng thanh tìm kiếm trên trang web để tìm kiếm các tài liệu học tập lượng giác theo từ khóa, chủ đề, hoặc lớp học.

Câu hỏi 11: Làm thế nào để sử dụng công cụ vẽ đồ thị hàm số lượng giác trên tic.edu.vn?

Bạn chỉ cần nhập biểu thức của hàm số lượng giác vào ô nhập liệu và nhấn nút “Vẽ đồ thị”. Công cụ sẽ tự động vẽ đồ thị của hàm số đó.

Câu hỏi 12: Làm thế nào để tham gia diễn đàn trao đổi học tập trên tic.edu.vn?

Bạn cần đăng ký một tài khoản trên trang web và sau đó truy cập vào diễn đàn để tham gia thảo luận.

Câu hỏi 13: Tôi có thể đóng góp tài liệu học tập cho tic.edu.vn không?

Chúng tôi luôn hoan nghênh sự đóng góp của bạn. Vui lòng liên hệ với chúng tôi qua email để biết thêm thông tin chi tiết.

Câu hỏi 14: Tic.edu.vn có tổ chức các khóa học lượng giác trực tuyến không?

Chúng tôi có thể tổ chức các khóa học lượng giác trực tuyến trong tương lai. Hãy theo dõi trang web của chúng tôi để cập nhật thông tin mới nhất.

Câu hỏi 15: Tic.edu.vn có hỗ trợ giải đáp bài tập lượng giác không?

Bạn có thể đặt câu hỏi về bài tập lượng giác trên diễn đàn của chúng tôi. Các thành viên khác và các giáo viên sẽ cố gắng giúp bạn giải đáp.

Câu hỏi 16: Làm thế nào để tôi có thể nhận được thông báo về các tài liệu và công cụ học tập mới nhất trên tic.edu.vn?

Bạn có thể đăng ký nhận bản tin của chúng tôi qua email để nhận được thông báo về các tài liệu và công cụ học tập mới nhất.

Câu hỏi 17: Tic.edu.vn có phiên bản di động không?

Chúng tôi đang phát triển phiên bản di động của trang web. Hãy theo dõi để biết thêm thông tin chi tiết.

Câu hỏi 18: Tic.edu.vn có thu phí sử dụng không?

Tất cả các tài liệu và công cụ học tập trên tic.edu.vn đều hoàn toàn miễn phí.

Câu hỏi 19: Tôi có thể liên hệ với ai nếu có thắc mắc hoặc góp ý về tic.edu.vn?

Bạn có thể liên hệ với chúng tôi qua email: [email protected].

Chúc bạn học tốt môn lượng giác!