Cho Hình Chóp S.ABCD Có Đáy ABCD Là Hình Chữ Nhật: A-Z

Cho Hình Chóp S.abcd Có đáy Abcd Là Hình Chữ Nhật mở ra vô vàn bài toán hình học thú vị, từ tính toán cơ bản đến chứng minh phức tạp. Hãy cùng tic.edu.vn khám phá sâu hơn về dạng hình này và cách chinh phục các bài tập liên quan.

1. Hình Chóp S.ABCD Đáy Hình Chữ Nhật Là Gì?

Hình chóp S.ABCD có đáy ABCD là hình chữ nhật là một hình chóp tứ giác đặc biệt, nơi đáy của nó là một hình chữ nhật. Điểm S là đỉnh của chóp, nằm ngoài mặt phẳng chứa đáy.

• Định nghĩa: Hình chóp S.ABCD là hình chóp có đáy ABCD là hình chữ nhật và S là đỉnh nằm ngoài mặt phẳng (ABCD).
• Các yếu tố:
  • Đáy: Hình chữ nhật ABCD.
  • Đỉnh: Điểm S.
  • Các cạnh bên: SA, SB, SC, SD.
  • Các mặt bên: SAB, SBC, SCD, SDA.
  • Đường cao: Đoạn thẳng SH vuông góc với mặt phẳng (ABCD), với H là chân đường cao.

2. Các Tính Chất Quan Trọng Của Hình Chóp S.ABCD Với Đáy Là Hình Chữ Nhật

Hình chóp S.ABCD với đáy là hình chữ nhật sở hữu những tính chất hình học đặc trưng, tạo nên sự thú vị trong việc nghiên cứu và giải toán. Dưới đây là một số tính chất quan trọng:

1. Tính chất về đáy: Đáy ABCD là hình chữ nhật, do đó có các cạnh đối song song và bằng nhau (AB // CD, AD // BC, AB = CD, AD = BC), các góc ở đỉnh đều là góc vuông (∠A = ∠B = ∠C = ∠D = 90°), và hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
2. Tính chất về đường cao: Đường cao SH vuông góc với mặt phẳng đáy (ABCD), tức là SH vuông góc với mọi đường thẳng nằm trong mặt phẳng (ABCD). Điều này rất quan trọng trong việc tính toán thể tích và khoảng cách.
3. Tính chất về các mặt bên: Các mặt bên của hình chóp (SAB, SBC, SCD, SDA) là các tam giác. Tùy thuộc vào vị trí của đỉnh S so với đáy ABCD, các tam giác này có thể là tam giác thường, tam giác cân, hoặc tam giác vuông.
4. Tính chất đặc biệt khi SA vuông góc với đáy: Nếu SA vuông góc với mặt phẳng (ABCD), thì SA là đường cao của hình chóp. Khi đó:
   • Tam giác SAB, SAC, SAD là các tam giác vuông tại A.
   • Việc tính toán trở nên đơn giản hơn vì có thể sử dụng định lý Pythagoras và các hệ thức lượng trong tam giác vuông.
5. Tính chất về các đường thẳng vuông góc: Trong nhiều bài toán, việc xác định các đường thẳng vuông góc với nhau là chìa khóa để giải quyết vấn đề. Ví dụ, nếu biết một đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong một mặt phẳng, thì đường thẳng đó vuông góc với mặt phẳng đó.

3. Các Dạng Bài Toán Thường Gặp Về Hình Chóp S.ABCD Đáy Hình Chữ Nhật

Hình chóp S.ABCD đáy hình chữ nhật là một chủ đề quen thuộc trong chương trình hình học không gian, và có rất nhiều dạng bài tập khác nhau liên quan đến nó. Dưới đây là một số dạng bài toán thường gặp:

1. Tính thể tích của hình chóp:

   • Yêu cầu: Tính thể tích của hình chóp S.ABCD khi biết độ dài các cạnh đáy và chiều cao.
   • Phương pháp: Sử dụng công thức tính thể tích hình chóp: V = (1/3) Sđáy h, trong đó Sđáy là diện tích đáy (hình chữ nhật) và h là chiều cao của hình chóp.

2. Tính diện tích xung quanh và diện tích toàn phần:

   • Yêu cầu: Tính diện tích xung quanh (tổng diện tích các mặt bên) và diện tích toàn phần (diện tích xung quanh cộng diện tích đáy).
   • Phương pháp: Tính diện tích từng mặt bên (tam giác) và cộng lại. Diện tích toàn phần bằng diện tích xung quanh cộng với diện tích hình chữ nhật ABCD.

3. Chứng minh các đường thẳng vuông góc, mặt phẳng vuông góc:

   • Yêu cầu: Chứng minh các quan hệ vuông góc giữa các đường thẳng và mặt phẳng trong hình chóp.
   • Phương pháp: Sử dụng các định lý và dấu hiệu nhận biết về quan hệ vuông góc trong không gian. Ví dụ: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau nằm trong một mặt phẳng thì đường thẳng đó vuông góc với mặt phẳng đó.

4. Xác định và tính góc giữa đường thẳng và mặt phẳng, giữa hai mặt phẳng:

   • Yêu cầu: Xác định và tính góc giữa đường thẳng và mặt phẳng, hoặc giữa hai mặt phẳng trong hình chóp.
   • Phương pháp: Sử dụng định nghĩa và các phương pháp tính góc trong không gian. Ví dụ: Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng.

5. Tính khoảng cách từ một điểm đến một đường thẳng hoặc mặt phẳng:

   • Yêu cầu: Tính khoảng cách từ một điểm (ví dụ: điểm A) đến một đường thẳng (ví dụ: đường thẳng SB) hoặc đến một mặt phẳng (ví dụ: mặt phẳng (SCD)).
   • Phương pháp: Sử dụng các công thức và phương pháp tính khoảng cách trong không gian. Ví dụ: Khoảng cách từ một điểm đến một mặt phẳng là độ dài đoạn vuông góc hạ từ điểm đó xuống mặt phẳng.

6. Bài toán liên quan đến thiết diện:

   • Yêu cầu: Xác định và tính diện tích thiết diện của hình chóp khi cắt bởi một mặt phẳng.
   • Phương pháp: Xác định các giao tuyến của mặt phẳng cắt với các mặt của hình chóp, từ đó xác định hình dạng của thiết diện và tính diện tích của nó.

7. Bài toán tổng hợp:

   • Yêu cầu: Kết hợp nhiều kiến thức và kỹ năng để giải quyết một bài toán phức tạp liên quan đến hình chóp S.ABCD.
   • Phương pháp: Phân tích kỹ đề bài, xác định các yếu tố đã biết và yếu tố cần tìm, lập kế hoạch giải và thực hiện từng bước một cách cẩn thận.

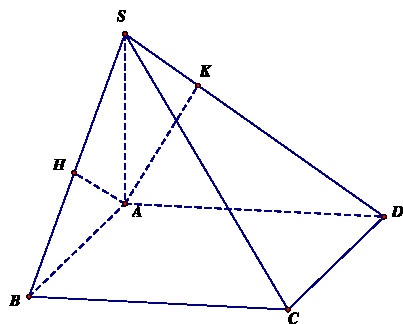Hình chóp S ABCD có đáy ABCD là hình chữ nhật và SA vuông góc với mặt phẳng đáy minh họa các yếu tố cơ bản

4. Bí Quyết Giải Nhanh Bài Tập Hình Chóp S.ABCD Đáy Hình Chữ Nhật

Để chinh phục các bài toán hình chóp S.ABCD đáy hình chữ nhật một cách nhanh chóng và hiệu quả, bạn cần trang bị cho mình những “bí kíp” sau đây:

1. Nắm vững lý thuyết:

   • Học thuộc các định nghĩa, tính chất, định lý liên quan đến hình chóp, hình chữ nhật, quan hệ vuông góc trong không gian.
   • Hiểu rõ các công thức tính diện tích, thể tích, khoảng cách, góc trong không gian.

2. Vẽ hình chính xác:

   • Vẽ hình rõ ràng, đầy đủ các yếu tố của hình chóp và hình chữ nhật.
   • Sử dụng thước và compa để vẽ các đường thẳng và đường tròn chính xác.
   • Biết cách vẽ hình biểu diễn của các hình không gian trên mặt phẳng.

3. Phân tích đề bài:

   • Đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán.
   • Phân tích mối quan hệ giữa các yếu tố, tìm ra hướng giải quyết bài toán.

4. Lựa chọn phương pháp giải phù hợp:

   • Sử dụng phương pháp tọa độ hóa nếu bài toán liên quan đến tính toán khoảng cách, góc.
   • Sử dụng phương pháp hình học thuần túy nếu bài toán yêu cầu chứng minh quan hệ vuông góc.
   • Sử dụng các định lý, hệ quả để giải nhanh các bài toán trắc nghiệm.

5. Rèn luyện kỹ năng tính toán:

   • Thực hiện các phép tính chính xác, cẩn thận.
   • Sử dụng máy tính bỏ túi để kiểm tra kết quả.

6. Luyện tập thường xuyên:

   • Giải nhiều bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán khác nhau.
   • Tham khảo các tài liệu, sách tham khảo để mở rộng kiến thức.

7. Sử dụng tài liệu và công cụ hỗ trợ từ tic.edu.vn:

   • Nguồn tài liệu đa dạng: tic.edu.vn cung cấp đầy đủ tài liệu về hình học không gian, bao gồm lý thuyết, bài tập, và đề thi mẫu.
   • Công cụ hỗ trợ học tập hiệu quả: Các công cụ tính toán trực tuyến, vẽ hình không gian, và giải bài tập từng bước giúp bạn học tập dễ dàng hơn.
   • Cộng đồng học tập sôi nổi: Tham gia diễn đàn, nhóm học tập để trao đổi kiến thức, kinh nghiệm với các bạn học sinh khác.

5. Ứng Dụng Thực Tế Của Hình Chóp S.ABCD Đáy Hình Chữ Nhật

Hình chóp S.ABCD với đáy là hình chữ nhật không chỉ là một khái niệm trừu tượng trong sách giáo khoa, mà còn có nhiều ứng dụng thực tế trong cuộc sống và các lĩnh vực khoa học kỹ thuật. Dưới đây là một số ví dụ điển hình:

1. Kiến trúc và xây dựng:

   • Thiết kế mái nhà: Mái nhà hình chóp giúp thoát nước tốt, chống thấm dột và tạo vẻ đẹp thẩm mỹ cho công trình.
   • Xây dựng kim tự tháp: Các kim tự tháp cổ đại là những công trình kiến trúc vĩ đại có hình dạng chóp, thể hiện sự vững chắc và trường tồn.
   • Thiết kế các công trình có không gian rộng: Hình chóp được sử dụng để tạo ra các không gian rộng lớn, không có cột chống ở giữa, như nhà thi đấu, nhà triển lãm, trung tâm thương mại.

2. Thiết kế đồ vật:

   • Bao bì sản phẩm: Các hộp đựng quà, hộp bánh kẹo có hình dạng chóp giúp bảo vệ sản phẩm và tạo sự hấp dẫn cho người mua.
   • Đèn trang trí: Đèn ngủ, đèn bàn có chụp đèn hình chóp tạo ra ánh sáng dịu nhẹ và ấm cúng.
   • Đồ chơi: Nhiều loại đồ chơi trẻ em có hình dạng chóp, giúp trẻ phát triển tư duy không gian và khả năng sáng tạo.

3. Ứng dụng trong khoa học:

   • Tinh thể học: Các tinh thể có cấu trúc hình học phức tạp, trong đó hình chóp là một thành phần cơ bản.
   • Địa chất học: Hình chóp được sử dụng để mô tả các cấu trúc địa chất như núi lửa, đồi, và các dạng địa hình khác.
   • Thiết kế ăng-ten: Ăng-ten hình chóp được sử dụng trong các hệ thống thông tin liên lạc để tăng cường khả năng thu và phát sóng.

4. Ứng dụng trong nghệ thuật:

   • Điêu khắc: Các tác phẩm điêu khắc có hình dạng chóp thể hiện sự mạnh mẽ, uy nghiêm và tính biểu tượng cao.
   • Hội họa: Các họa sĩ sử dụng hình chóp để tạo ra các hiệu ứng không gian và chiều sâu trong tranh vẽ.

6. Các Định Lý Và Công Thức Cần Nhớ Về Hình Chóp S.ABCD

Để giải quyết các bài toán liên quan đến hình chóp S.ABCD một cách hiệu quả, việc nắm vững các định lý và công thức là vô cùng quan trọng. Dưới đây là một số định lý và công thức quan trọng mà bạn cần ghi nhớ:

6.1. Định lý về đường thẳng vuông góc với mặt phẳng

• Định lý 1: Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng nằm trong một mặt phẳng, thì đường thẳng đó vuông góc với mặt phẳng đó.
  • Ứng dụng: Chứng minh đường thẳng vuông góc với mặt phẳng.
• Định lý 2: Nếu một mặt phẳng chứa một đường thẳng vuông góc với một mặt phẳng khác, thì hai mặt phẳng đó vuông góc với nhau.
  • Ứng dụng: Chứng minh hai mặt phẳng vuông góc.

6.2. Định lý ba đường vuông góc

• Cho đường thẳng a không nằm trong mặt phẳng (P) và vuông góc với (P) tại điểm O. Gọi b là một đường thẳng nằm trong (P) và không vuông góc với a. Gọi H là hình chiếu của A trên b. Khi đó, AH vuông góc với b khi và chỉ khi OH vuông góc với b.
  • Ứng dụng: Tìm hình chiếu vuông góc của một điểm trên một đường thẳng hoặc mặt phẳng.

6.3. Công thức tính diện tích

• Diện tích hình chữ nhật: S = a * b, trong đó a và b là độ dài hai cạnh của hình chữ nhật.
• Diện tích tam giác: S = (1/2) a h, trong đó a là độ dài cạnh đáy và h là chiều cao tương ứng.
• Diện tích xung quanh hình chóp: Sxq = tổng diện tích các mặt bên.
• Diện tích toàn phần hình chóp: Stp = Sxq + Sđáy.

6.4. Công thức tính thể tích

• Thể tích hình chóp: V = (1/3) Sđáy h, trong đó Sđáy là diện tích đáy và h là chiều cao của hình chóp.

6.5. Công thức tính khoảng cách

• Khoảng cách từ một điểm đến một mặt phẳng: d(A, (P)) = |Ax0 + By0 + Cz0 + D| / √(A^2 + B^2 + C^2), trong đó A(x0, y0, z0) là tọa độ điểm A và Ax + By + Cz + D = 0 là phương trình mặt phẳng (P).
• Khoảng cách giữa hai đường thẳng chéo nhau: d(a, b) = |[u, v].MN| / |[u, v]|, trong đó u và v là vectơ chỉ phương của hai đường thẳng a và b, M thuộc a, N thuộc b, và [u, v] là tích có hướng của u và v.

6.6. Công thức tính góc

• Góc giữa đường thẳng và mặt phẳng: sin(α) = |(u.n)| / (|u| * |n|), trong đó u là vectơ chỉ phương của đường thẳng và n là vectơ pháp tuyến của mặt phẳng.
• Góc giữa hai mặt phẳng: cos(α) = |(n1.n2)| / (|n1| * |n2|), trong đó n1 và n2 là vectơ pháp tuyến của hai mặt phẳng.

7. Ví Dụ Minh Họa Các Bài Toán Về Hình Chóp S.ABCD

Để giúp bạn hiểu rõ hơn về cách áp dụng các kiến thức đã học vào giải bài tập, dưới đây là một số ví dụ minh họa về các dạng toán thường gặp liên quan đến hình chóp S.ABCD:

Ví dụ 1:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = a, AD = a√2. Cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.

a) Tính thể tích của hình chóp S.ABCD.

b) Tính góc giữa đường thẳng SC và mặt phẳng (ABCD).

Giải:

a) Thể tích của hình chóp S.ABCD:

• Diện tích đáy ABCD: Sđáy = AB AD = a a√2 = a^2√2.
• Chiều cao SA = a.
• Thể tích V = (1/3) Sđáy SA = (1/3) a^2√2 a = (a^3√2) / 3.

b) Góc giữa đường thẳng SC và mặt phẳng (ABCD):

• Gọi O là giao điểm của AC và BD.
• Hình chiếu của SC trên mặt phẳng (ABCD) là AC.
• Góc giữa SC và (ABCD) là góc SCA.
• Tam giác SAC vuông tại A, ta có: tan(SCA) = SA / AC = a / √(a^2 + 2a^2) = a / (a√3) = 1/√3.
• Vậy góc SCA = 30°.

Ví dụ 2:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AB = a, BC = a√3. Cạnh SA vuông góc với mặt phẳng (ABCD) và SA = 2a. Gọi M là trung điểm của SC.

a) Chứng minh rằng mặt phẳng (MBD) vuông góc với mặt phẳng (SAC).

b) Tính khoảng cách từ điểm A đến mặt phẳng (MBD).

Giải:

a) Chứng minh (MBD) ⊥ (SAC):

• Trong mặt phẳng (SAC), kẻ MO cắt SA tại I.
• Ta có: MO // SA (do M là trung điểm SC và O là trung điểm AC).
• Suy ra: MO ⊥ (ABCD) => MO ⊥ BD.
• Mà BD ⊥ AC (tính chất hình chữ nhật).
• Do đó: BD ⊥ (SAC).
• Vì BD nằm trong mặt phẳng (MBD) nên (MBD) ⊥ (SAC).

b) Tính khoảng cách từ A đến (MBD):

• Gọi H là hình chiếu của A trên BD.
• Ta có: AH ⊥ BD.
• Vì BD ⊥ (SAC) nên BD ⊥ AM.
• Suy ra: AM ⊥ (MBD).
• Vậy khoảng cách từ A đến (MBD) là AH.
• Tính AH:
  • 1/AH^2 = 1/AD^2 + 1/AB^2 = 1/(3a^2) + 1/a^2 = 4/(3a^2).
  • AH = (a√3) / 2.

Ví dụ 3:

Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Gọi O là giao điểm của AC và BD. Biết SO vuông góc với mặt phẳng (ABCD) và SO = a√3. Tính góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD).

Giải:

• Gọi M là trung điểm của BC. Khi đó OM // AB và OM = AB/2 = a/2.
• Vì SO ⊥ (ABCD) nên SO ⊥ OM.
• Do đó, góc giữa (SBC) và (ABCD) là góc SMO.
• Trong tam giác SOM vuông tại O:
  • tan(SMO) = SO/OM = (a√3) / (a/2) = 2√3.
  • Vậy góc SMO = arctan(2√3).

8. Lời Khuyên Từ Các Chuyên Gia Giáo Dục Trên tic.edu.vn

Các chuyên gia giáo dục tại tic.edu.vn chia sẻ những lời khuyên hữu ích để bạn học tốt hình học không gian, đặc biệt là dạng toán về hình chóp S.ABCD đáy hình chữ nhật:

1. Học lý thuyết một cách có hệ thống: Thay vì học thuộc lòng, hãy cố gắng hiểu bản chất của các định nghĩa, định lý, và tính chất. Điều này giúp bạn áp dụng chúng một cách linh hoạt vào giải các bài tập khác nhau.
2. Tập trung vào việc vẽ hình: Kỹ năng vẽ hình tốt là yếu tố then chốt để giải quyết các bài toán hình học không gian. Hãy luyện tập vẽ hình thường xuyên để nâng cao khả năng hình dung và biểu diễn các đối tượng trong không gian.
3. Giải bài tập từ dễ đến khó: Bắt đầu với các bài tập cơ bản để làm quen với các khái niệm và công thức. Sau đó, dần dần chuyển sang các bài tập phức tạp hơn để thử thách khả năng của bản thân.
4. Tìm kiếm sự giúp đỡ khi cần thiết: Đừng ngần ngại hỏi thầy cô, bạn bè, hoặc tham gia các diễn đàn, nhóm học tập để được giải đáp thắc mắc và chia sẻ kinh nghiệm.
5. Sử dụng các nguồn tài liệu tham khảo uy tín: tic.edu.vn là một nguồn tài liệu học tập đáng tin cậy với đầy đủ lý thuyết, bài tập, đề thi mẫu, và các công cụ hỗ trợ học tập hiệu quả.
6. Rèn luyện tính kiên trì và cẩn thận: Hình học không gian đòi hỏi sự kiên trì, cẩn thận, và tỉ mỉ. Hãy luôn giữ thái độ tích cực và không nản lòng trước những bài toán khó.

9. Tại Sao Nên Học Hình Học Không Gian Trên tic.edu.vn?

tic.edu.vn là một nền tảng học tập trực tuyến hàng đầu tại Việt Nam, cung cấp đầy đủ các khóa học và tài liệu về hình học không gian, đặc biệt là dạng toán về hình chóp S.ABCD đáy hình chữ nhật. Dưới đây là những lý do bạn nên lựa chọn tic.edu.vn để học hình học không gian:

1. Đội ngũ giáo viên giàu kinh nghiệm: Các khóa học trên tic.edu.vn được giảng dạy bởi đội ngũ giáo viên giỏi, có nhiều năm kinh nghiệm trong lĩnh vực giáo dục và luyện thi.
2. Nội dung bài giảng chất lượng cao: Các bài giảng được thiết kế khoa học, dễ hiểu, và bám sát chương trình sách giáo khoa.
3. Hệ thống bài tập đa dạng: tic.edu.vn cung cấp hàng ngàn bài tập từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng đề thi khác nhau.
4. Công cụ hỗ trợ học tập hiệu quả: Các công cụ tính toán trực tuyến, vẽ hình không gian, và giải bài tập từng bước giúp bạn học tập dễ dàng và hiệu quả hơn.
5. Cộng đồng học tập sôi nổi: Tham gia diễn đàn, nhóm học tập để trao đổi kiến thức, kinh nghiệm với các bạn học sinh khác.
6. Học mọi lúc, mọi nơi: Bạn có thể học tập trên tic.edu.vn mọi lúc, mọi nơi, chỉ cần có kết nối internet.
7. Chi phí hợp lý: tic.edu.vn cung cấp các khóa học với mức giá cạnh tranh, phù hợp với túi tiền của nhiều đối tượng học sinh, sinh viên.

10. FAQ – Các Câu Hỏi Thường Gặp Về Hình Chóp S.ABCD

1. Làm thế nào để tính thể tích hình chóp S.ABCD khi biết đáy ABCD là hình chữ nhật và chiều cao SH?

Để tính thể tích hình chóp S.ABCD, bạn sử dụng công thức: V = (1/3) Sđáy h, trong đó Sđáy là diện tích hình chữ nhật ABCD và h là chiều cao SH của hình chóp.

2. Làm sao để chứng minh một đường thẳng vuông góc với một mặt phẳng trong hình chóp S.ABCD?

Bạn cần chứng minh đường thẳng đó vuông góc với hai đường thẳng cắt nhau nằm trong mặt phẳng đó.

3. Làm thế nào để tìm góc giữa đường thẳng và mặt phẳng trong hình chóp S.ABCD?

Bạn tìm hình chiếu của đường thẳng trên mặt phẳng, sau đó góc giữa đường thẳng và hình chiếu của nó là góc cần tìm.

4. Công thức tính diện tích xung quanh của hình chóp S.ABCD là gì?

Diện tích xung quanh của hình chóp là tổng diện tích của các mặt bên (các tam giác SAB, SBC, SCD, SDA).

5. Làm thế nào để tính khoảng cách từ một điểm đến một mặt phẳng trong hình chóp S.ABCD?

Bạn có thể sử dụng công thức khoảng cách từ một điểm đến một mặt phẳng trong không gian tọa độ, hoặc tìm đường thẳng vuông góc từ điểm đó đến mặt phẳng.

6. Tại sao cần nắm vững các định lý về quan hệ vuông góc trong không gian khi giải bài tập về hình chóp S.ABCD?

Các định lý về quan hệ vuông góc giúp bạn xác định và chứng minh các yếu tố vuông góc trong hình chóp, từ đó giải quyết các bài toán liên quan đến khoảng cách, góc, và thể tích.

7. Làm thế nào để vẽ hình biểu diễn của hình chóp S.ABCD trên mặt phẳng giấy?

Bạn cần tuân thủ các quy tắc vẽ hình biểu diễn trong hình học họa hình, đảm bảo tính trực quan và dễ nhìn của hình vẽ.

8. Các dạng bài tập nào thường gặp nhất về hình chóp S.ABCD đáy hình chữ nhật?

Các dạng bài tập thường gặp bao gồm tính thể tích, diện tích, chứng minh quan hệ vuông góc, tính góc giữa đường thẳng và mặt phẳng, và các bài toán liên quan đến thiết diện.

9. Làm thế nào để học tốt hình học không gian nói chung và dạng toán về hình chóp S.ABCD nói riêng?

Bạn cần nắm vững lý thuyết, luyện tập vẽ hình, giải bài tập từ dễ đến khó, và tìm kiếm sự giúp đỡ khi cần thiết.

10. tic.edu.vn có thể giúp tôi học tốt hình học không gian như thế nào?

tic.edu.vn cung cấp đầy đủ các khóa học, tài liệu, công cụ hỗ trợ học tập, và cộng đồng học tập sôi nổi, giúp bạn học tập hiệu quả và đạt kết quả cao trong môn hình học không gian.

Kết Luận

Hình chóp S.ABCD với đáy là hình chữ nhật là một chủ đề quan trọng trong chương trình hình học không gian. Để chinh phục dạng toán này, bạn cần nắm vững lý thuyết, rèn luyện kỹ năng giải bài tập, và sử dụng các nguồn tài liệu tham khảo uy tín. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất. Hãy bắt đầu hành trình khám phá hình học không gian đầy thú vị và bổ ích ngay bây giờ!