**Cách Chứng Minh Hai Tam Giác Vuông Bằng Nhau Hiệu Quả Nhất**

Bạn đang tìm kiếm Cách Chứng Minh Hai Tam Giác Vuông Bằng Nhau một cách dễ dàng và hiệu quả? Bài viết này của tic.edu.vn sẽ cung cấp cho bạn kiến thức đầy đủ, chi tiết và dễ hiểu nhất về các trường hợp bằng nhau của tam giác vuông. Từ đó, giúp bạn chinh phục các bài toán hình học một cách tự tin. Khám phá ngay những bí quyết và mẹo học hữu ích để làm chủ kiến thức này nhé!

1. Khái Niệm Cơ Bản Về Tam Giác Bằng Nhau

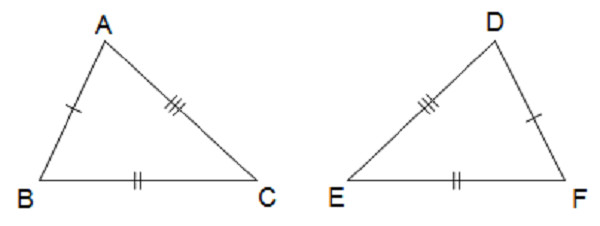
Hai tam giác được gọi là bằng nhau nếu chúng có các cạnh tương ứng bằng nhau và các góc tương ứng bằng nhau. Nói một cách đơn giản, nếu bạn có thể “xếp chồng” hai tam giác lên nhau một cách hoàn hảo thì chúng là hai tam giác bằng nhau. Để biểu thị sự bằng nhau của tam giác ABC và tam giác DFE, ta viết: ΔABC = ΔDFE.

Hai tam giác bằng nhau, thể hiện sự tương đồng về kích thước và hình dạng.

2. Các Trường Hợp Bằng Nhau Của Tam Giác Vuông – Bí Quyết Nắm Vững

Tam giác vuông là một dạng tam giác đặc biệt với một góc vuông (90 độ). Nhờ đặc điểm này, việc chứng minh hai tam giác vuông bằng nhau trở nên đơn giản hơn so với tam giác thường. Dưới đây là các trường hợp bằng nhau của tam giác vuông mà bạn cần nắm vững:

2.1. Trường Hợp Cạnh Góc Vuông – Cạnh Góc Vuông (c.g.c)

Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Trường hợp này dựa trên tiên đề cạnh – góc – cạnh (c.g.c) trong tam giác thường.

2.2. Trường Hợp Cạnh Góc Vuông – Góc Nhọn Kề (g.c.g)

Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. Trường hợp này dựa trên tiên đề góc – cạnh – góc (g.c.g) trong tam giác thường.

2.3. Trường Hợp Cạnh Huyền – Góc Nhọn (cạnh huyền, góc nhọn)

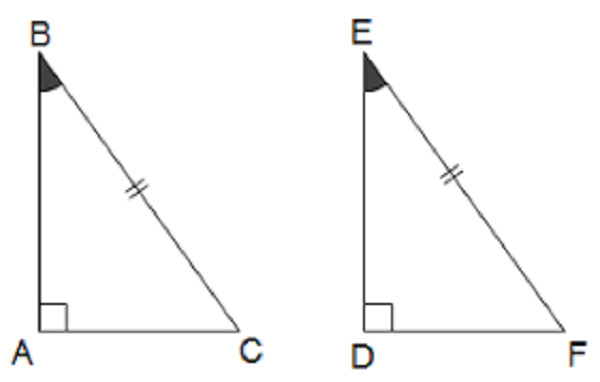
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Hai tam giác vuông bằng nhau khi có cạnh huyền và góc nhọn tương ứng bằng nhau.

2.4. Trường Hợp Cạnh Huyền – Cạnh Góc Vuông (cạnh huyền, cạnh góc vuông)

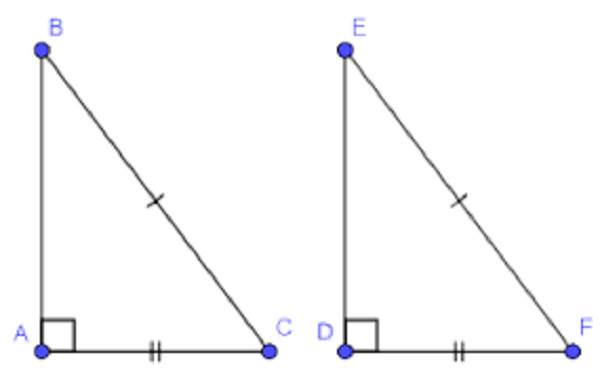
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.

Hai tam giác vuông bằng nhau khi cạnh huyền và một cạnh góc vuông tương ứng bằng nhau.

3. Các Dạng Bài Tập Thường Gặp Về Chứng Minh Tam Giác Vuông Bằng Nhau

Để giúp bạn hiểu rõ hơn về các trường hợp bằng nhau của tam giác vuông, chúng ta sẽ cùng nhau khám phá các dạng bài tập thường gặp và cách giải quyết chúng một cách hiệu quả.

3.1. Dạng 1: Chứng Minh Hai Tam Giác Vuông Bằng Nhau Trực Tiếp

Đây là dạng bài tập cơ bản nhất, yêu cầu bạn áp dụng trực tiếp các trường hợp bằng nhau của tam giác vuông để chứng minh hai tam giác vuông cho trước là bằng nhau.

Phương pháp giải:

1. Xác định hai tam giác vuông cần chứng minh bằng nhau.
2. Kiểm tra xem hai tam giác vuông đã có những yếu tố nào bằng nhau (cạnh, góc).
3. Đối chiếu với các trường hợp bằng nhau của tam giác vuông để xác định trường hợp phù hợp.
4. Trình bày bài giải một cách rõ ràng, logic, chỉ ra các yếu tố bằng nhau và kết luận hai tam giác vuông bằng nhau theo trường hợp nào.

3.2. Dạng 2: Chứng Minh Các Đoạn Thẳng Hoặc Góc Bằng Nhau Thông Qua Tam Giác Vuông Bằng Nhau

Dạng bài tập này yêu cầu bạn chứng minh hai đoạn thẳng hoặc hai góc bằng nhau bằng cách chứng minh hai tam giác vuông chứa các đoạn thẳng hoặc góc đó bằng nhau.

Phương pháp giải:

1. Xác định hai đoạn thẳng hoặc hai góc cần chứng minh bằng nhau.
2. Tìm hai tam giác vuông chứa hai đoạn thẳng hoặc hai góc đó.
3. Chứng minh hai tam giác vuông đó bằng nhau (sử dụng các trường hợp bằng nhau của tam giác vuông).
4. Suy ra hai đoạn thẳng hoặc hai góc tương ứng bằng nhau (do hai tam giác bằng nhau).

3.3. Dạng 3: Tìm Điều Kiện Để Hai Tam Giác Vuông Bằng Nhau

Dạng bài tập này yêu cầu bạn tìm thêm các điều kiện cần thiết để hai tam giác vuông cho trước trở nên bằng nhau.

Phương pháp giải:

1. Xác định hai tam giác vuông cần xét.
2. Liệt kê các yếu tố đã biết của hai tam giác vuông.
3. Dựa vào các trường hợp bằng nhau của tam giác vuông, xác định những yếu tố còn thiếu để hai tam giác vuông bằng nhau.
4. Nêu các điều kiện cần bổ sung để hai tam giác vuông bằng nhau theo một trường hợp cụ thể.

4. Ví Dụ Minh Họa Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Để giúp bạn hiểu sâu hơn về cách áp dụng các trường hợp bằng nhau của tam giác vuông vào giải bài tập, chúng ta sẽ cùng nhau phân tích một số ví dụ điển hình.

Ví dụ 1:

Cho tam giác ABC vuông tại A, có AB = AC. Gọi M là trung điểm của BC. Chứng minh rằng:

a) ΔAMB = ΔAMC

b) AM là tia phân giác của góc BAC.

Giải:

a) Xét hai tam giác vuông AMB và AMC, ta có:

• AB = AC (giả thiết)
• AM là cạnh chung
• BM = CM (M là trung điểm của BC)

=> ΔAMB = ΔAMC (cạnh – cạnh – cạnh)

b) Vì ΔAMB = ΔAMC (chứng minh trên)

=> Góc BAM = Góc CAM (hai góc tương ứng)

=> AM là tia phân giác của góc BAC.

Ví dụ 2:

Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm D sao cho BD = BA. Kẻ đường thẳng d vuông góc với BC tại D. Đường thẳng d cắt AC tại E. Chứng minh rằng AE = DE.

Giải:

Xét ΔABD có BA = BD nên ΔABD cân tại B.

=> Góc BAD = Góc BDA (tính chất tam giác cân)

Vì ΔABC vuông tại A nên góc BAC + góc ABC = 90 độ

Vì ED ⊥ BC nên góc EDB + góc ADE = 90 độ

Mà góc BAC = góc EDB = 90 độ

=> Góc ABC = góc ADE

Xét ΔABE và ΔDBE, ta có:

• Góc BAE = góc BDE = 90 độ
• BE là cạnh chung
• Góc ABE = góc DBE (chứng minh trên)

=> ΔABE = ΔDBE (cạnh huyền – góc nhọn)

=> AE = DE (hai cạnh tương ứng)

Ví dụ 3:

Cho tam giác ABC vuông tại A, tia phân giác của góc B cắt AC ở D. Kẻ DH vuông góc với BC (H thuộc BC). Chứng minh rằng ΔABD = ΔHBD.

Giải:

Xét ΔABD và ΔHBD, ta có:

• Góc BAD = góc BHD = 90 độ
• BD là cạnh chung
• Góc ABD = góc HBD (vì BD là tia phân giác của góc B)

=> ΔABD = ΔHBD (cạnh huyền – góc nhọn)

5. Bài Tập Thực Hành Về Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập, hãy cùng nhau thử sức với một số bài tập thực hành sau đây:

Bài 1: Cho tam giác ABC vuông tại A, có AB = AC. Gọi I là trung điểm của BC. Chứng minh rằng AI vuông góc với BC.

Bài 2: Cho tam giác ABC có góc A = 90 độ. Trên cạnh BC lấy điểm D sao cho AB = BD. Qua D kẻ đường thẳng vuông góc với BC, cắt AC tại E. Chứng minh rằng BE là tia phân giác của góc ABC.

Bài 3: Cho tam giác ABC vuông tại A. Vẽ AH vuông góc với BC (H thuộc BC). Trên tia đối của tia HA lấy điểm D sao cho HD = HA. Chứng minh rằng:

a) BC là tia phân giác của góc ABD.

b) Tam giác BCD là tam giác cân.

6. Mẹo Học Tốt Các Trường Hợp Bằng Nhau Của Tam Giác Vuông

Để học tốt và ghi nhớ lâu các trường hợp bằng nhau của tam giác vuông, bạn có thể áp dụng một số mẹo sau:

• Học thuộc định nghĩa và các trường hợp bằng nhau: Đây là bước cơ bản nhất để có thể áp dụng vào giải bài tập.
• Vẽ hình minh họa: Việc vẽ hình minh họa cho từng trường hợp sẽ giúp bạn hình dung rõ hơn và ghi nhớ lâu hơn.
• Làm nhiều bài tập: Thực hành giải nhiều bài tập khác nhau sẽ giúp bạn rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
• Ôn tập thường xuyên: Ôn tập lại kiến thức đã học một cách thường xuyên sẽ giúp bạn củng cố kiến thức và tránh quên.
• Tìm kiếm sự giúp đỡ: Nếu gặp khó khăn trong quá trình học tập, đừng ngần ngại tìm kiếm sự giúp đỡ từ thầy cô, bạn bè hoặc các nguồn tài liệu trực tuyến.

7. Tại Sao Nên Học Về Các Trường Hợp Bằng Nhau Của Tam Giác Vuông Tại Tic.edu.vn?

Tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập phong phú và chất lượng cho học sinh, sinh viên và giáo viên. Khi học về các trường hợp bằng nhau của tam giác vuông tại tic.edu.vn, bạn sẽ nhận được những lợi ích sau:

• Tài liệu đầy đủ và chi tiết: tic.edu.vn cung cấp đầy đủ các kiến thức về định nghĩa, các trường hợp bằng nhau, các dạng bài tập và ví dụ minh họa.
• Giải thích dễ hiểu: Các kiến thức được trình bày một cách rõ ràng, logic và dễ hiểu, giúp bạn dễ dàng tiếp thu và nắm vững.
• Bài tập đa dạng: tic.edu.vn cung cấp nhiều bài tập thực hành với các mức độ khác nhau, giúp bạn rèn luyện kỹ năng giải bài tập.
• Cập nhật thường xuyên: Các tài liệu trên tic.edu.vn được cập nhật thường xuyên để đảm bảo tính chính xác và phù hợp với chương trình học hiện hành.
• Cộng đồng hỗ trợ: tic.edu.vn có một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, hỏi đáp và nhận được sự giúp đỡ từ những người khác.
• Miễn phí: Hầu hết các tài liệu trên tic.edu.vn đều được cung cấp miễn phí, giúp bạn tiết kiệm chi phí học tập.

Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc sử dụng các nguồn tài liệu trực tuyến chất lượng cao như tic.edu.vn cung cấp sự hỗ trợ đáng kể cho việc học tập và nâng cao kết quả học tập của học sinh.

8. Lời Kêu Gọi Hành Động (Call to Action)

Bạn đang gặp khó khăn trong việc học hình học và đặc biệt là chứng minh hai tam giác vuông bằng nhau? Đừng lo lắng! Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Với tic.edu.vn, việc học toán sẽ trở nên dễ dàng và thú vị hơn bao giờ hết.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn

9. Câu Hỏi Thường Gặp (FAQ) Về Chứng Minh Tam Giác Vuông Bằng Nhau

Dưới đây là một số câu hỏi thường gặp về chứng minh tam giác vuông bằng nhau và câu trả lời chi tiết:

1. Có bao nhiêu trường hợp bằng nhau của tam giác vuông?

Có tổng cộng 4 trường hợp bằng nhau của tam giác vuông: cạnh góc vuông – cạnh góc vuông, cạnh góc vuông – góc nhọn kề, cạnh huyền – góc nhọn, cạnh huyền – cạnh góc vuông.

2. Làm thế nào để xác định trường hợp bằng nhau phù hợp để chứng minh hai tam giác vuông bằng nhau?

Bạn cần kiểm tra xem hai tam giác vuông đã có những yếu tố nào bằng nhau (cạnh, góc) và đối chiếu với các trường hợp bằng nhau của tam giác vuông để xác định trường hợp phù hợp.

3. Khi nào thì sử dụng trường hợp cạnh huyền – cạnh góc vuông để chứng minh hai tam giác vuông bằng nhau?

Bạn sử dụng trường hợp cạnh huyền – cạnh góc vuông khi biết cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia.

4. Trường hợp cạnh góc vuông – góc nhọn kề có gì khác so với trường hợp góc – cạnh – góc trong tam giác thường?

Trong tam giác vuông, “cạnh góc vuông” đã bao gồm thông tin về góc vuông (90 độ), do đó trường hợp cạnh góc vuông – góc nhọn kề tương đương với trường hợp góc – cạnh – góc trong tam giác thường.

5. Làm thế nào để chứng minh hai đoạn thẳng hoặc hai góc bằng nhau thông qua tam giác vuông bằng nhau?

Bạn cần tìm hai tam giác vuông chứa hai đoạn thẳng hoặc hai góc đó, chứng minh hai tam giác vuông đó bằng nhau, và suy ra hai đoạn thẳng hoặc hai góc tương ứng bằng nhau (do hai tam giác bằng nhau).

6. Nếu không có đủ yếu tố để chứng minh hai tam giác vuông bằng nhau theo một trường hợp cụ thể, tôi nên làm gì?

Bạn cần tìm thêm các yếu tố bằng nhau khác (ví dụ: sử dụng các tính chất của tam giác cân, tam giác đều, đường trung tuyến, đường phân giác, đường cao, v.v.) hoặc chứng minh các yếu tố bằng nhau đó trước khi áp dụng các trường hợp bằng nhau của tam giác vuông.

7. Có những lỗi sai nào thường gặp khi chứng minh hai tam giác vuông bằng nhau?

Một số lỗi sai thường gặp bao gồm: nhầm lẫn giữa các trường hợp bằng nhau, sử dụng sai các tính chất của tam giác vuông, không chứng minh đầy đủ các yếu tố cần thiết, và trình bày bài giải không rõ ràng, logic.

8. Làm thế nào để cải thiện kỹ năng chứng minh hình học, đặc biệt là chứng minh tam giác vuông bằng nhau?

Để cải thiện kỹ năng chứng minh hình học, bạn cần học thuộc các định nghĩa, định lý, tính chất, làm nhiều bài tập, ôn tập thường xuyên, và tìm kiếm sự giúp đỡ khi cần thiết.

9. Tic.edu.vn có những tài liệu và công cụ gì để hỗ trợ việc học về chứng minh tam giác vuông bằng nhau?

Tic.edu.vn cung cấp đầy đủ các kiến thức về định nghĩa, các trường hợp bằng nhau, các dạng bài tập, ví dụ minh họa, bài tập thực hành, và cộng đồng hỗ trợ. Ngoài ra, tic.edu.vn có thể cung cấp các công cụ hỗ trợ như công cụ vẽ hình, công cụ tính toán, và công cụ kiểm tra đáp án.

10. Tôi có thể tìm kiếm sự giúp đỡ từ ai khi gặp khó khăn trong việc học về chứng minh tam giác vuông bằng nhau trên tic.edu.vn?

Bạn có thể tìm kiếm sự giúp đỡ từ thầy cô, bạn bè, cộng đồng học tập trên tic.edu.vn, hoặc gửi câu hỏi trực tiếp cho đội ngũ hỗ trợ của tic.edu.vn.

10. Kết Luận

Nắm vững cách chứng minh hai tam giác vuông bằng nhau là một kỹ năng quan trọng trong học toán hình học. Với những kiến thức, ví dụ và bài tập thực hành được cung cấp trong bài viết này, tic.edu.vn hy vọng bạn sẽ tự tin hơn trong việc chinh phục các bài toán hình học và đạt được kết quả học tập tốt nhất. Đừng quên truy cập tic.edu.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác nhé!