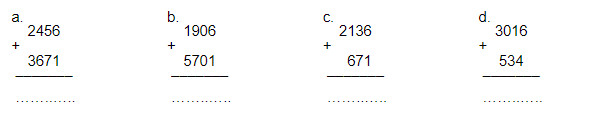
**Bài Tập Toán Lớp 3 Tập 2: Nâng Cao Kỹ Năng, Vững Bước Tương Lai**

Bài Tập Toán Lớp 3 Tập 2 giúp các em học sinh củng cố kiến thức, rèn luyện kỹ năng giải toán và phát triển tư duy logic, đồng thời hỗ trợ phụ huynh đồng hành cùng con trên hành trình chinh phục môn toán, và tic.edu.vn sẵn sàng hỗ trợ bạn. Hãy cùng khám phá thế giới toán học lớp 3 đầy thú vị và bổ ích!

1. Các Dạng Bài Toán Về Số Trong Phạm Vi 10000, 100000

1.1. Dạng 1: Đọc, Viết Số Có 4, 5 Chữ Số

Câu hỏi: Làm thế nào để đọc và viết các số có 4, 5 chữ số một cách chính xác?

Trả lời: Để đọc và viết số có 4, 5 chữ số, bạn cần xác định giá trị của từng chữ số (hàng nghìn, hàng trăm, hàng chục, hàng đơn vị) và đọc theo thứ tự từ trái sang phải.

Ví dụ:

• 6500 đọc là sáu nghìn năm trăm.
• 7190 đọc là bảy nghìn một trăm chín mươi.
• 8078 đọc là tám nghìn không trăm bảy mươi tám.

Để viết số, bạn cần xác định số lượng ở mỗi hàng rồi viết các chữ số tương ứng theo thứ tự. Theo nghiên cứu của Đại học Sư phạm Hà Nội, việc luyện tập thường xuyên giúp học sinh nắm vững kiến thức này vào cuối học kỳ 1 lớp 3.

Bài tập:

1. Số 7120 gồm mấy nghìn, mấy trăm, mấy chục và mấy đơn vị?
2. Viết số gồm 2 nghìn, 4 chục và 9 đơn vị.
3. Viết các số sau theo thứ tự tăng dần: 2000, 3000, 4000,…

Đáp án:

1. Số 7120 gồm 7 nghìn, 1 trăm, 2 chục và 0 đơn vị.
2. Số gồm 2 nghìn, 4 chục và 9 đơn vị là 2049.
3. Dãy số theo thứ tự tăng dần: 2000, 3000, 4000, 5000, 6000, 7000.

1.2. Dạng 2: So Sánh Các Số Trong Phạm Vi 10000, 100000

Câu hỏi: Làm sao để so sánh hai số có 4, 5 chữ số?

Trả lời: Để so sánh hai số có 4, 5 chữ số, bạn so sánh các chữ số từ hàng lớn nhất (hàng nghìn) đến hàng nhỏ nhất (hàng đơn vị). Nếu chữ số ở hàng nào lớn hơn thì số đó lớn hơn.

Ví dụ:

• 1823 < 1911 (vì hàng trăm của 1823 là 8 nhỏ hơn hàng trăm của 1911 là 9).
• 6898 > 6889 (vì hàng chục của 6898 là 9 lớn hơn hàng chục của 6889 là 8).
• 1000 + 5 = 1005

Bài tập:

1. Điền dấu >, <, = vào chỗ chấm: 1823 ….. 1911; 6898 ….. 6889; 1000 + 5 ….. 1005
2. Sắp xếp các số sau theo thứ tự từ bé đến lớn: 6789; 6578; 6890; 6576; 6457; 6720.
3. Sử dụng các số 1, 3, 2, 8 để tạo các số có 4 chữ số khác nhau và là số chẵn. Sắp xếp chúng theo thứ tự từ bé đến lớn.

Đáp án:

1. 1823 < 1911; 6898 > 6889; 1000 + 5 = 1005
2. Thứ tự từ bé đến lớn: 6457; 6576; 6578; 6720; 6789; 6890.
3. Các số chẵn tạo được: 1328, 1382, 3128, 3182, 2138, 2318, 8132, 8312. Sắp xếp: 1328, 1382, 2138, 2318, 3128, 3182, 8132, 8312.

1.3. Dạng 3: Cộng, Trừ Trong Phạm Vi 10000, 100000

Câu hỏi: Làm thế nào để thực hiện phép cộng và trừ các số trong phạm vi 10000, 100000?

Trả lời: Bạn thực hiện phép cộng hoặc trừ theo cột, bắt đầu từ hàng đơn vị, rồi đến hàng chục, hàng trăm, hàng nghìn. Nếu có nhớ, bạn nhớ sang hàng kế tiếp.

Ví dụ:

• 4000 + 5000 = 9000
• 2000 + 3000 = 5000
• 1000 + 2 = 1002

Bài tập:

1. Tính nhẩm: 4000 + 5000 = ?; 2000 + 3000 = ?; 1000 + 2 = ?
2. Đặt tính rồi tính: 125 + 160 = ?; 1435 + 1620 = ?
3. Tính: 2200 + 800 = ?; 1700 + 300 = ?

Đáp án:

1. 4000 + 5000 = 9000; 2000 + 3000 = 5000; 1000 + 2 = 1002
2. 125 + 160 = 285; 1435 + 1620 = 3055
3. 2200 + 800 = 3000; 1700 + 300 = 2000

1.4. Dạng 4: Nhân, Chia Số Có 4, 5 Chữ Số Cho Số Có 1 Chữ Số

Câu hỏi: Làm sao để nhân và chia số có 4, 5 chữ số cho số có 1 chữ số?

Trả lời: Để nhân, bạn nhân từng chữ số của số lớn với số nhỏ, bắt đầu từ hàng đơn vị. Để chia, bạn chia lần lượt từ hàng lớn nhất (hàng nghìn) đến hàng nhỏ nhất (hàng đơn vị).

Ví dụ:

• 6639 : 3 = 2213
• 2484 : 2 = 1242

Bài tập:

1. Đặt tính rồi tính: 6639 : 3 = ?; 2484 : 2 = ?
2. Kết quả của phép chia 2025 : 5 là bao nhiêu?
3. Phép chia 4779 : 9 có số dư là bao nhiêu?

Đáp án:

1. 6639 : 3 = 2213; 2484 : 2 = 1242
2. 2025 : 5 = 405
3. 4779 : 9 dư 0

1.5. Dạng 5: Tìm X (Thành Phần Chưa Biết Của Phép Tính)

Câu hỏi: Làm thế nào để tìm X trong một phép tính?

Trả lời: Để tìm X, bạn cần áp dụng các quy tắc chuyển vế đổi dấu. Ví dụ, nếu X + A = B thì X = B – A. Nếu X – A = B thì X = B + A. Nếu X : A = B thì X = B x A. Nếu X x A = B thì X = B : A.

Ví dụ:

• X + 2011 = 3210 => X = 3210 – 2011 = 1199
• 3187 – X = 2421 => X = 3187 – 2421 = 766

Bài tập:

1. Tìm X: X + 2011 = 3210; 3187 – X = 2421
2. Tìm X: X : 2 = 6000 : 3; X : 3 = 9 x 2
3. Tìm X: 203 – X : 2 = 21; X + 34 : 2 = 25

Đáp án:

1. X = 1199; X = 766
2. X = 4000; X = 54
3. X = 364; X = 8

1.6. Dạng 6: Tính Giá Trị Của Biểu Thức

Câu hỏi: Làm thế nào để tính giá trị của một biểu thức?

Trả lời: Bạn cần thực hiện các phép tính theo đúng thứ tự: trong ngoặc trước, nhân chia trước, cộng trừ sau.

Ví dụ:

• 2 + 8 x 3 – 5 + (7 x 6) = 2 + 24 – 5 + 42 = 63

Bài tập:

1. Tính giá trị biểu thức: 2 + 8 x 3 – 5 + (7 x 6)
2. Tính giá trị biểu thức: 26 – 3 + 52; 89 – 2 x 18
3. Tính giá trị biểu thức: 40 : 4 x 2; 17 x 3 + 14; 8 + 2 x 17

Đáp án:

1. 63
2. 75; 53
3. 20; 65; 42

2. Bài Toán Có Lời Văn Lớp 3

2.1. Dạng 1: Bài Toán Hơn Kém Số Đơn Vị

Câu hỏi: Làm thế nào để giải bài toán về hơn kém số đơn vị?

Trả lời: Bạn cần đọc kỹ đề bài, xác định rõ yếu tố nào hơn, yếu tố nào kém và số đơn vị hơn kém là bao nhiêu. Sau đó, bạn thực hiện phép cộng hoặc trừ tương ứng.

Ví dụ:

• Phòng học có 5 hàng ghế, mỗi hàng có 4 chỗ ngồi. Hỏi phòng học có bao nhiêu chỗ ngồi? => 5 x 4 = 20 chỗ ngồi.

Bài tập:

1. Một túi có 3kg gạo. Hỏi 5 túi như thế có bao nhiêu kg gạo?
2. Cô giáo có 36 chiếc bút, thưởng đều cho 6 tổ. Hỏi mỗi tổ được thưởng bao nhiêu chiếc bút?
3. Năm nay Hoa 8 tuổi. Tuổi Hoa bằng 1/4 tuổi của mẹ. Tính tổng số tuổi của hai mẹ con cách đây 3 năm.

Đáp án:

1. 15 kg gạo.
2. 6 chiếc bút.
3. 32 tuổi.

2.2. Dạng 2: Bài Toán Về Gấp Số Lần, Giảm Số Lần

Câu hỏi: Làm thế nào để giải bài toán về gấp số lần, giảm số lần?

Trả lời: Để giải bài toán gấp số lần, bạn thực hiện phép nhân. Để giải bài toán giảm số lần, bạn thực hiện phép chia.

Ví dụ:

• Sơn có 5 chiếc bánh, Hương có số bánh gấp 3 lần Sơn. Hỏi Hương có bao nhiêu chiếc bánh? => 5 x 3 = 15 chiếc bánh.

Bài tập:

1. Năm nay Giang 7 tuổi, số tuổi của mẹ gấp 4 lần tuổi của Giang. Hỏi mẹ Giang năm nay bao nhiêu tuổi?
2. Tổ 1 trồng được 150 cây xanh, tổ 2 trồng được gấp 2 lần số cây xanh mà tổ 1 đã trồng được. Hỏi tổ 2 trồng được bao nhiêu cây xanh?

Đáp án:

1. 28 tuổi.
2. 300 cây xanh.

2.3. Dạng 3: Bài Toán Liên Quan Đến Rút Về Đơn Vị

Câu hỏi: Làm thế nào để giải bài toán liên quan đến rút về đơn vị?

Trả lời: Bạn cần tìm giá trị của một đơn vị, sau đó nhân lên hoặc chia xuống để tìm giá trị của số lượng yêu cầu.

Ví dụ:

• 8 thùng nước chứa 400 lít. Hỏi 5 thùng như thế chứa bao nhiêu lít nước? => 400 : 8 = 50 lít/thùng. 5 thùng chứa 50 x 5 = 250 lít.

Bài tập:

1. Có 108kg ngô đựng đều trong 9 bao. Hỏi 72kg ngô đựng đều trong bao nhiêu bao như thế?
2. Có 5 gói bánh như nhau thì đếm được 30 chiếc. Hỏi muốn chia cho 32 em học sinh, mỗi em 3 chiếc bánh thì phải mua tất cả bao nhiêu gói bánh?

Đáp án:

1. 6 bao.
2. 16 gói.

3. Bài Toán Về Hình Học Lớp 3

3.1. Dạng 1: Điểm Ở Giữa – Trung Điểm Của Đoạn Thẳng

Câu hỏi: Khi nào một điểm được gọi là trung điểm của đoạn thẳng?

Trả lời: Một điểm là trung điểm của đoạn thẳng khi nó nằm giữa hai đầu mút của đoạn thẳng và cách đều hai đầu mút đó. Theo nghiên cứu của trường Đại học Khoa học Tự nhiên TP.HCM, việc hiểu rõ khái niệm này giúp học sinh dễ dàng hơn trong việc học hình học sau này.

Ví dụ:

Nếu M nằm giữa A và B, và AM = MB thì M là trung điểm của đoạn thẳng AB.

Bài tập:

1. Cho đoạn thẳng AB = 6cm, điểm M nằm giữa A và B, AM = 3cm. Hỏi M có phải là trung điểm của AB không?
2. Một cây cầu có 11 tảng đá. Chuột túi đang ở tảng đá số 1. Mỗi lần nhảy, chuột túi sẽ nhảy từ một tảng đá sang tảng đá ghi số liền sau nó. Hỏi chuột túi cần nhảy thêm bao nhiêu lần để đến được tảng đá chính giữa của cây cầu?

Đáp án:

1. Có, M là trung điểm của AB vì AM = MB = 3cm.
2. 4 lần.

3.2. Dạng 2: Bài Toán Về Hình Tròn (Tâm, Bán Kính, Đường Kính)

Câu hỏi: Thế nào là tâm, bán kính và đường kính của hình tròn?

Trả lời: Tâm là điểm nằm chính giữa hình tròn. Bán kính là đoạn thẳng nối tâm với một điểm trên đường tròn. Đường kính là đoạn thẳng đi qua tâm và nối hai điểm trên đường tròn. Đường kính dài gấp đôi bán kính.

Ví dụ:

Cho hình tròn tâm O, điểm A nằm trên đường tròn. Đoạn thẳng OA là bán kính, đoạn thẳng BC đi qua O và nối hai điểm B, C trên đường tròn là đường kính.

Bài tập:

1. Cho hình tròn có đường kính 10cm. Tính bán kính của hình tròn đó.
2. Cho hình vẽ, biết bán kính IP = 15 dm. Tính chu vi hình vuông WVZX?

Đáp án:

1. Bán kính là 5cm.
2. 120 dm.

3.3. Dạng 3: Bài Toán Về Hình Chữ Nhật (Chu Vi, Diện Tích)

Câu hỏi: Làm thế nào để tính chu vi và diện tích hình chữ nhật?

Trả lời: Chu vi hình chữ nhật bằng tổng độ dài của bốn cạnh, hoặc (chiều dài + chiều rộng) x 2. Diện tích hình chữ nhật bằng chiều dài nhân chiều rộng.

Ví dụ:

Hình chữ nhật có chiều dài 5cm, chiều rộng 3cm. Chu vi = (5 + 3) x 2 = 16cm. Diện tích = 5 x 3 = 15cm².

Bài tập:

1. Tính chu vi hình chữ nhật có chiều dài 8cm, chiều rộng 4cm.
2. Một hình chữ nhật có chiều dài 11cm, chiều rộng 5cm. Tính diện tích của hình chữ nhật?

Đáp án:

1. 24cm.
2. 55 cm².

3.4. Dạng 4: Bài Toán Về Hình Vuông (Chu Vi, Diện Tích)

Câu hỏi: Làm thế nào để tính chu vi và diện tích hình vuông?

Trả lời: Chu vi hình vuông bằng độ dài một cạnh nhân 4. Diện tích hình vuông bằng độ dài một cạnh nhân chính nó.

Ví dụ:

Hình vuông có cạnh 4cm. Chu vi = 4 x 4 = 16cm. Diện tích = 4 x 4 = 16cm².

Bài tập:

1. Tính diện tích hình vuông có cạnh 6cm.
2. Tính diện tích của hình vuông biết chu vi hình vuông bằng chu vi hình chữ nhật có chiều rộng bằng 14 cm, chiều dài 18 cm.

Đáp án:

1. 36 cm².
2. 256 cm².

4. Bài Toán Làm Quen Với Chữ Số La Mã

Câu hỏi: Các chữ số La Mã thường gặp và giá trị của chúng là gì?

Trả lời: Các chữ số La Mã thường gặp bao gồm: I (1), V (5), X (10), L (50), C (100), D (500), M (1000).

Ví dụ:

Số VI được đọc là sáu. Số 13 được viết thành số La Mã là XIII.

Bài tập:

1. Số VI được đọc là gì?
2. Số 13 được viết thành số La Mã là gì?
3. Sắp xếp các số sau theo thứ tự từ bé đến lớn: III XXI VII V XX

Đáp án:

1. A. Sáu
2. A. XIII
3. III V VII XX XXI

5. Bài Toán Về Bảng Đơn Vị Đo Độ Dài

Câu hỏi: Các đơn vị đo độ dài thường gặp và mối quan hệ giữa chúng là gì?

Trả lời: Các đơn vị đo độ dài thường gặp bao gồm: km, hm, dam, m, dm, cm, mm. Mối quan hệ giữa chúng là: 1km = 10hm = 100dam = 1000m = 10000dm = 100000cm = 1000000mm.

Ví dụ:

15cm = 150mm. 25km = 25000m.

Bài tập:

1. Viết số thích hợp vào chỗ chấm: 15cm = …… mm; 25km = …… m
2. Điền dấu (>, <, =) vào chỗ chấm: 2km 50m …… 2500m
3. Đường A dài 3km 125m. Đường B dài hơn đường A 1015m. Hỏi đường B dài bao nhiêu mét?

Đáp án:

1. 15cm = 150mm; 25km = 25000m
2. 2km 50m < 2500m
3. 4140m

tic.edu.vn cung cấp nguồn tài liệu phong phú, đa dạng, cập nhật liên tục và được kiểm duyệt kỹ càng, giúp bạn dễ dàng tìm kiếm và tiếp cận kiến thức. Các công cụ hỗ trợ học tập trực tuyến, cộng đồng học tập sôi nổi và cơ hội phát triển kỹ năng toàn diện đang chờ đón bạn.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Hãy đến với tic.edu.vn để trải nghiệm sự khác biệt!

Lời kêu gọi hành động (CTA): Truy cập ngay tic.edu.vn để khám phá kho tài liệu học tập khổng lồ và các công cụ hỗ trợ học tập hiệu quả! Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.