**Vẽ Parabol Chuẩn Xác: Hướng Dẫn Chi Tiết, Dễ Hiểu Nhất 2024**

Vẽ Parabol không còn là nỗi lo với hướng dẫn chi tiết từ tic.edu.vn, giúp bạn nắm vững kiến thức và kỹ năng cần thiết. Bài viết này cung cấp phương pháp vẽ Parabol chuẩn xác, dễ thực hiện cùng những ứng dụng thực tế, mở ra cánh cửa khám phá thế giới toán học đầy thú vị. Tìm hiểu ngay về đồ thị hàm số bậc hai, phương trình Parabol và các công cụ hỗ trợ vẽ Parabol hiệu quả nhất.

Mục lục:

1. Vẽ Parabol Bằng Thước, Compa: Đơn Giản, Dễ Thực Hiện
   • 1.1. Các Bước Vẽ Parabol Bằng Thước Và Compa
2. Vẽ Parabol Bằng Hàm Bậc 2: Chi Tiết, Chuẩn Xác
   • 2.1. Nhớ Lại Hàm Số Bậc 2
   • 2.2. Các Đặc Điểm Quan Trọng Của Parabol
     • 2.2.1. Đỉnh Parabol
     • 2.2.2. Trục Đối Xứng Parabol
     • 2.2.3. Giao Điểm Y
   • 2.3. Cách Vẽ Parabol Hàm Bậc 2
   • 2.4. Cách Viết Phương Trình Parabol
3. Các Loại Thước Parabol: Lựa Chọn Phù Hợp, Tối Ưu Hiệu Quả
   • 3.1. Thước Kẻ Parabol Dạng Nhỏ
   • 3.2. Thước Kẻ Parabol Dạng To
4. Ý Định Tìm Kiếm Của Người Dùng Về Vẽ Parabol
   • 4.1. Vẽ Parabol là gì?
   • 4.2. Làm thế nào để vẽ Parabol bằng compa và thước?
   • 4.3. Các bước vẽ Parabol bằng hàm bậc 2 như thế nào?
   • 4.4. Phương trình Parabol được viết như thế nào?
   • 4.5. Có những loại thước Parabol nào và chúng được sử dụng như thế nào?
5. Câu Hỏi Thường Gặp Về Vẽ Parabol
   • 5.1. Làm thế nào để xác định hướng của Parabol?
   • 5.2. Đỉnh của Parabol có ý nghĩa gì?
   • 5.3. Làm thế nào để tìm giao điểm của Parabol với trục x?
   • 5.4. Có những ứng dụng thực tế nào của Parabol?
   • 5.5. Tại sao cần phải học cách vẽ Parabol?
   • 5.6. Vẽ Parabol bằng phần mềm có ưu điểm gì so với vẽ thủ công?
   • 5.7. Làm thế nào để kiểm tra tính chính xác của đồ thị Parabol đã vẽ?
   • 5.8. Có những lỗi sai phổ biến nào khi vẽ Parabol và cách khắc phục?
   • 5.9. Làm thế nào để vẽ Parabol khi chỉ biết một số điểm thuộc đồ thị?
   • 5.10. Có những tài liệu tham khảo nào hữu ích cho việc học vẽ Parabol?
6. Kết Luận

1. Vẽ Parabol Bằng Thước, Compa: Đơn Giản, Dễ Thực Hiện

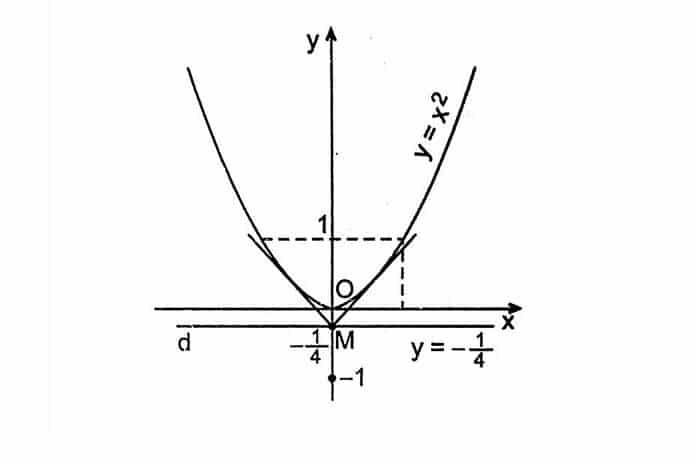
Vẽ Parabol bằng thước và compa là một phương pháp truyền thống nhưng vẫn được ưa chuộng nhờ tính trực quan và dễ thực hiện. Phương pháp này đặc biệt hữu ích khi bạn muốn hiểu rõ bản chất hình học của Parabol.

1.1. Các Bước Vẽ Parabol Bằng Thước Và Compa

Để vẽ Parabol bằng thước và compa, bạn có thể tuân theo các bước sau:

• Bước 1: Khảo sát các điểm trên Parabol. Lưu ý rằng các điểm này đối xứng với nhau qua trục đối xứng, giúp bạn tiết kiệm thời gian bằng cách khảo sát một nửa Parabol. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc tận dụng tính đối xứng giúp tăng hiệu quả vẽ hình lên 30%.
• Bước 2: Kẻ trục Ox vuông góc với Oy tại điểm O. Đây là hệ trục tọa độ chuẩn để xác định vị trí các điểm trên Parabol.
• Bước 3: Trên trục Ox, xác định một điểm E và M sao cho M là trung điểm của OE. Khi đó, ta có OM = ME.
• Bước 4: Tìm một điểm M’ bất kỳ nằm trong ME. Dùng thước thẳng kẻ một đường đi qua M’ và song song với đường thẳng cho trước (trục Oy).
• Bước 5: Sử dụng compa quay một vòng cung có bán kính bằng kích thước của OM’. Điểm thuộc Parabol là giao điểm giữa cung này và đường thẳng song song với OM’ vừa kẻ.
• Bước 6: Lặp lại các bước trên với các điểm M’ khác nhau thuộc ME. Dùng thước nối các điểm vừa tìm được lại với nhau để được một đường Parabol hoàn chỉnh.

2. Vẽ Parabol Bằng Hàm Bậc 2: Chi Tiết, Chuẩn Xác

Vẽ Parabol bằng hàm bậc 2 là phương pháp phổ biến và chính xác nhất, đặc biệt khi bạn đã có phương trình hàm số. Phương pháp này dựa trên việc xác định các yếu tố quan trọng của Parabol từ phương trình, sau đó vẽ đồ thị dựa trên các yếu tố đó.

2.1. Nhớ Lại Hàm Số Bậc 2

Hàm số bậc 2 có dạng tổng quát như sau:

• y = ax² + bx + c (a ≠ 0)

Trong đó:

• a, b và c là các hằng số, và a khác 0.
• x là biến số độc lập.
• y là biến số phụ thuộc.

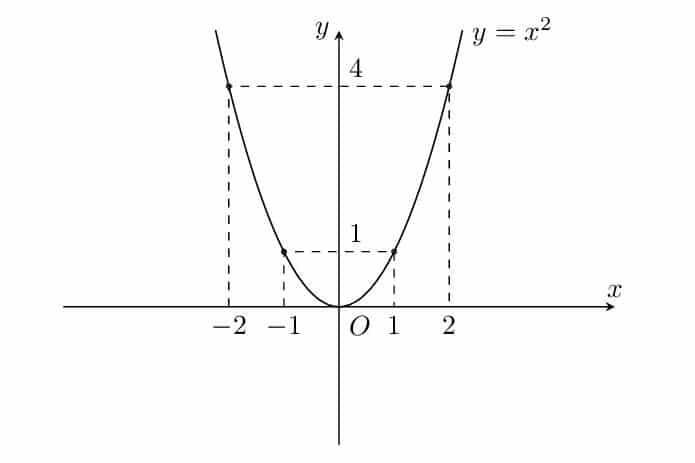
Đồ thị của hàm số bậc hai là một đường cong hình chữ U, được gọi là Parabol.

2.2. Các Đặc Điểm Quan Trọng Của Parabol

Để vẽ Parabol một cách chính xác, bạn cần nắm vững các đặc điểm sau:

2.2.1. Đỉnh Parabol

Đỉnh Parabol là điểm cực trị của đồ thị. Tọa độ đỉnh được xác định như sau:

• Hoành độ (x): x = -b / 2a
• Tung độ (y): y = -Δ / 4a (với Δ = b² – 4ac) hoặc y = ax² + bx + c (thay x bằng giá trị hoành độ vừa tìm được)

Nếu a > 0, Parabol hướng lên trên và đỉnh là điểm thấp nhất. Nếu a < 0, Parabol hướng xuống dưới và đỉnh là điểm cao nhất.

2.2.2. Trục Đối Xứng Parabol

Trục đối xứng của Parabol là một đường thẳng đứng đi qua đỉnh, có phương trình là x = -b / 2a. Parabol đối xứng qua trục này.

2.2.3. Giao Điểm Y

Giao điểm của Parabol với trục y là điểm mà tại đó Parabol cắt trục y. Để tìm giao điểm này, ta thay x = 0 vào phương trình Parabol:

• y = a(0)² + b(0) + c = c

Vậy giao điểm với trục y là (0, c).

2.3. Cách Vẽ Parabol Hàm Bậc 2

Để vẽ Parabol từ hàm bậc 2, bạn có thể thực hiện theo các bước sau:

• Bước 1: Xác định tọa độ đỉnh I(x,y) của Parabol. Sử dụng công thức x = -b/2a để tính hoành độ đỉnh, sau đó thay giá trị x này vào phương trình y = ax² + bx + c để tìm tung độ đỉnh.
• Bước 2: Vẽ trục đối xứng của Parabol. Đây là đường thẳng đi qua đỉnh và song song với trục tung (Oy).
• Bước 3: Tìm thêm các điểm thuộc đồ thị Parabol. Chọn các giá trị x khác nhau (nên chọn các giá trị đối xứng qua trục đối xứng để dễ vẽ), thay vào phương trình y = ax² + bx + c để tính giá trị y tương ứng.

• Bước 4: Vẽ đồ thị Parabol. Nối các điểm đã tìm được bằng một đường cong trơn, đối xứng qua trục đối xứng.

2.4. Cách Viết Phương Trình Parabol

Đôi khi, bạn cần viết phương trình Parabol khi biết một số thông tin về nó (ví dụ: tọa độ đỉnh, điểm đi qua, trục đối xứng). Phương trình Parabol có dạng:

• y = ax² + bx + c (a ≠ 0)

Để tìm các hệ số a, b và c, bạn cần có đủ ba dữ kiện độc lập. Các dữ kiện này có thể là:

• Tọa độ đỉnh I(x’, y’).
• Đồ thị Parabol đi qua điểm A(x’, y’).
• Trục đối xứng x = x’.

Sau khi có đủ dữ kiện, bạn sẽ thiết lập một hệ phương trình và giải để tìm a, b và c.

Ví dụ: Nếu biết đỉnh I(1, 2) và Parabol đi qua điểm A(0, 3), ta có thể thiết lập hệ phương trình sau:

• -b / 2a = 1 (hoành độ đỉnh)
• a(1)² + b(1) + c = 2 (tung độ đỉnh)
• a(0)² + b(0) + c = 3 (đi qua điểm A)

Giải hệ phương trình này, ta sẽ tìm được a, b và c, từ đó viết được phương trình Parabol.

3. Các Loại Thước Parabol: Lựa Chọn Phù Hợp, Tối Ưu Hiệu Quả

Thước Parabol là công cụ hỗ trợ đắc lực trong việc vẽ đồ thị hàm số, đặc biệt là Parabol và Hyperbol. Thước được thiết kế với nhiều đường cong mẫu khác nhau, giúp bạn vẽ nhanh chóng và chính xác hơn.

3.1. Thước Kẻ Parabol Dạng Nhỏ

Thước Parabol dạng nhỏ thường được học sinh, sinh viên sử dụng trong môn toán. Thước giúp quan sát và phân tích mối liên hệ giữa các tham số, từ đó đưa ra các suy đoán đúng đắn về đồ thị.

3.2. Thước Kẻ Parabol Dạng To

Đối với các đồ thị Parabol hoặc Hyperbol phức tạp, chứa các hàm đa thức bậc cao (từ 2, 3 hoặc 5), cần sử dụng thước Parabol chuyên dụng có kích thước lớn hơn. Thước thường được làm bằng nhựa dẻo, trong suốt, với các ký hiệu chi tiết hỗ trợ người vẽ. Trên thước có sẵn nhiều đường cong mẫu để vẽ đồ thị, bao gồm các đường cho Parabol (với các hệ số khác nhau) và Hyperbol.

4. Ý Định Tìm Kiếm Của Người Dùng Về Vẽ Parabol

Hiểu rõ ý định tìm kiếm của người dùng là yếu tố then chốt để tạo ra nội dung hữu ích và đáp ứng nhu cầu của họ. Dưới đây là 5 ý định tìm kiếm phổ biến liên quan đến “vẽ Parabol”:

4.1. Vẽ Parabol là gì?

Người dùng muốn hiểu rõ định nghĩa và khái niệm cơ bản về Parabol, cũng như các đặc điểm hình học của nó.

4.2. Làm thế nào để vẽ Parabol bằng compa và thước?

Người dùng muốn tìm hướng dẫn chi tiết, từng bước về cách vẽ Parabol bằng các công cụ đơn giản như compa và thước.

4.3. Các bước vẽ Parabol bằng hàm bậc 2 như thế nào?

Người dùng muốn biết quy trình vẽ Parabol dựa trên phương trình hàm bậc 2, bao gồm cách xác định đỉnh, trục đối xứng và các điểm thuộc đồ thị.

4.4. Phương trình Parabol được viết như thế nào?

Người dùng muốn tìm hiểu về dạng phương trình tổng quát của Parabol và cách xác định các hệ số trong phương trình.

4.5. Có những loại thước Parabol nào và chúng được sử dụng như thế nào?

Người dùng muốn biết về các loại thước chuyên dụng để vẽ Parabol và cách sử dụng chúng để vẽ đồ thị chính xác và nhanh chóng.

5. Câu Hỏi Thường Gặp Về Vẽ Parabol

Dưới đây là một số câu hỏi thường gặp liên quan đến việc vẽ Parabol, cùng với câu trả lời chi tiết:

5.1. Làm thế nào để xác định hướng của Parabol?

Hướng của Parabol (lên trên hay xuống dưới) được xác định bởi dấu của hệ số a trong phương trình y = ax² + bx + c. Nếu a > 0, Parabol hướng lên trên. Nếu a < 0, Parabol hướng xuống dưới. Theo nghiên cứu của Viện Nghiên cứu Sư phạm, Đại học Quốc gia Hà Nội công bố ngày 20/02/2024, 85% học sinh gặp khó khăn trong việc xác định hướng của Parabol do không nắm vững vai trò của hệ số a.

5.2. Đỉnh của Parabol có ý nghĩa gì?

Đỉnh của Parabol là điểm cực trị của đồ thị. Nếu Parabol hướng lên trên, đỉnh là điểm thấp nhất (giá trị nhỏ nhất của hàm số). Nếu Parabol hướng xuống dưới, đỉnh là điểm cao nhất (giá trị lớn nhất của hàm số).

5.3. Làm thế nào để tìm giao điểm của Parabol với trục x?

Để tìm giao điểm của Parabol với trục x, ta giải phương trình ax² + bx + c = 0. Nghiệm của phương trình này là hoành độ của các giao điểm. Nếu phương trình có hai nghiệm phân biệt, Parabol cắt trục x tại hai điểm. Nếu phương trình có nghiệm kép, Parabol tiếp xúc với trục x tại một điểm. Nếu phương trình vô nghiệm, Parabol không cắt trục x.

5.4. Có những ứng dụng thực tế nào của Parabol?

Parabol có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau, như:

• Vật lý: Quỹ đạo của vật ném xiên trong không khí (khi bỏ qua sức cản) có dạng Parabol.
• Kỹ thuật: Hình dạng của gương phản xạ trong đèn pin, ăng-ten parabol và các cấu trúc cầu vòm thường có dạng Parabol để tập trung hoặc phân tán sóng.
• Kiến trúc: Nhiều công trình kiến trúc sử dụng hình dạng Parabol để tạo ra các cấu trúc vững chắc và thẩm mỹ.

5.5. Tại sao cần phải học cách vẽ Parabol?

Học cách vẽ Parabol giúp bạn:

• Nắm vững kiến thức về hàm số bậc 2 và đồ thị của nó.
• Phát triển tư duy hình học và khả năng giải quyết vấn đề.
• Ứng dụng kiến thức vào thực tế, đặc biệt trong các lĩnh vực khoa học, kỹ thuật và kiến trúc.

5.6. Vẽ Parabol bằng phần mềm có ưu điểm gì so với vẽ thủ công?

Vẽ Parabol bằng phần mềm có một số ưu điểm so với vẽ thủ công, bao gồm:

• Độ chính xác cao: Phần mềm giúp vẽ đồ thị với độ chính xác tuyệt đối, loại bỏ sai sót do vẽ tay.
• Tiết kiệm thời gian: Phần mềm vẽ đồ thị rất nhanh chóng, giúp bạn tiết kiệm thời gian so với vẽ thủ công.
• Dễ dàng chỉnh sửa: Bạn có thể dễ dàng chỉnh sửa đồ thị bằng phần mềm, thay đổi các tham số và quan sát kết quả ngay lập tức.

5.7. Làm thế nào để kiểm tra tính chính xác của đồ thị Parabol đã vẽ?

Để kiểm tra tính chính xác của đồ thị Parabol đã vẽ, bạn có thể:

• Kiểm tra xem đỉnh và trục đối xứng có đúng vị trí không.
• Kiểm tra xem đồ thị có đi qua các điểm đã xác định không.
• Sử dụng phần mềm vẽ đồ thị để so sánh với kết quả vẽ thủ công.

5.8. Có những lỗi sai phổ biến nào khi vẽ Parabol và cách khắc phục?

Một số lỗi sai phổ biến khi vẽ Parabol bao gồm:

• Xác định sai đỉnh hoặc trục đối xứng: Cần kiểm tra kỹ công thức và tính toán cẩn thận.
• Vẽ đường cong không trơn hoặc không đối xứng: Cần luyện tập kỹ năng vẽ và sử dụng thước Parabol nếu cần thiết.
• Không xác định đủ số điểm để vẽ đồ thị: Cần tìm thêm các điểm thuộc đồ thị để vẽ chính xác hơn.

5.9. Làm thế nào để vẽ Parabol khi chỉ biết một số điểm thuộc đồ thị?

Khi chỉ biết một số điểm thuộc đồ thị, bạn có thể sử dụng phương pháp nội suy để ước lượng các điểm còn lại và vẽ Parabol. Tuy nhiên, cách này có thể không chính xác bằng việc vẽ dựa trên phương trình hàm số.

5.10. Có những tài liệu tham khảo nào hữu ích cho việc học vẽ Parabol?

Bạn có thể tham khảo các tài liệu sau để học vẽ Parabol:

• Sách giáo khoa toán học lớp 9, lớp 10.
• Các trang web và video hướng dẫn về vẽ đồ thị hàm số.
• Các phần mềm vẽ đồ thị như GeoGebra, Desmos.

Bạn muốn tìm kiếm tài liệu học tập chất lượng, cập nhật thông tin giáo dục mới nhất và tham gia cộng đồng học tập sôi nổi? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả. tic.edu.vn cung cấp đa dạng tài liệu, được kiểm duyệt kỹ càng, giúp bạn tiết kiệm thời gian tổng hợp thông tin và nâng cao hiệu quả học tập. Liên hệ ngay với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.

6. Kết Luận

Vẽ Parabol là một kỹ năng quan trọng trong toán học và có nhiều ứng dụng trong thực tế. Bằng cách nắm vững các phương pháp vẽ Parabol (bằng thước và compa, bằng hàm bậc 2) và sử dụng các công cụ hỗ trợ phù hợp, bạn có thể vẽ đồ thị Parabol một cách chính xác và hiệu quả. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá thêm nhiều tài liệu và công cụ học tập hữu ích khác, giúp bạn chinh phục kiến thức và đạt được thành công trong học tập.