Vẽ Hình Thang Cân: Bí Quyết & Ứng Dụng Từ A Đến Z

Hình thang cân là một hình học thú vị và quan trọng trong chương trình Toán học. Bạn muốn khám phá cách Vẽ Hình Thang Cân một cách chính xác, dễ hiểu và ứng dụng nó vào giải các bài toán hình học? Hãy cùng tic.edu.vn khám phá bí quyết và ứng dụng của hình thang cân ngay sau đây, đồng thời tiếp cận nguồn tài liệu học tập phong phú và công cụ hỗ trợ hiệu quả.

1. Hình Thang Cân Là Gì? Định Nghĩa & Tính Chất

Hình thang cân là một tứ giác đặc biệt, vừa mang đặc điểm của hình thang, vừa sở hữu thêm những tính chất đối xứng thú vị. Hiểu rõ định nghĩa và tính chất của nó là chìa khóa để vẽ và giải quyết các bài toán liên quan một cách hiệu quả.

1.1. Định Nghĩa Hình Thang Cân

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Điều này có nghĩa là nếu ABCD là hình thang (AB // CD) và góc C = góc D (hoặc góc A = góc B), thì ABCD là hình thang cân. Theo “Hình học 8” của tác giả Tạ Hoàng Bửu, xuất bản năm 2023, định nghĩa này là cơ sở để nhận biết và chứng minh một hình thang là hình thang cân.

1.2. Tính Chất Của Hình Thang Cân

Hình thang cân sở hữu những tính chất đặc biệt, giúp chúng ta dễ dàng nhận biết và sử dụng trong các bài toán:

• Tính chất 1: Trong hình thang cân, hai cạnh bên bằng nhau. (AD = BC)
• Tính chất 2: Trong hình thang cân, hai đường chéo bằng nhau. (AC = BD)
• Tính chất 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.
• Tính chất 4: Trong hình thang cân, hai góc kề một đáy bằng nhau.

1.3. Dấu Hiệu Nhận Biết Hình Thang Cân

Để nhận biết một hình thang có phải là hình thang cân hay không, ta có thể dựa vào các dấu hiệu sau:

• Dấu hiệu 1: Hình thang có hai góc kề một đáy bằng nhau là hình thang cân.
• Dấu hiệu 2: Hình thang có hai đường chéo bằng nhau là hình thang cân.
• Dấu hiệu 3: Hình thang có hai cạnh bên bằng nhau và hai góc kề một đáy bằng nhau là hình thang cân.

2. Các Cách Vẽ Hình Thang Cân Đơn Giản & Chính Xác

Có nhiều cách để vẽ hình thang cân, tùy thuộc vào thông tin đã cho. Dưới đây là một số phương pháp phổ biến và dễ thực hiện.

2.1. Vẽ Hình Thang Cân Khi Biết Hai Đáy Và Chiều Cao

Đây là phương pháp cơ bản nhất để vẽ hình thang cân.

Bước 1: Vẽ đoạn thẳng CD (đáy lớn) có độ dài cho trước.
Bước 2: Vẽ đường thẳng vuông góc với CD tại trung điểm I của CD. Đường thẳng này là trục đối xứng của hình thang cân.
Bước 3: Trên đường thẳng vuông góc, lấy điểm O sao cho OI bằng chiều cao của hình thang.
Bước 4: Vẽ đường thẳng AB (đáy nhỏ) đi qua O và song song với CD.
Bước 5: Chọn hai điểm A và B trên đường thẳng AB sao cho AB có độ dài cho trước và A, B đối xứng nhau qua đường thẳng IO.
Bước 6: Nối A với D và B với C ta được hình thang cân ABCD.

2.2. Vẽ Hình Thang Cân Khi Biết Đáy Lớn, Cạnh Bên Và Đường Chéo

Đây là phương pháp thường gặp trong các bài toán hình học.

Bước 1: Vẽ đoạn thẳng CD (đáy lớn) có độ dài cho trước.
Bước 2: Dựng đường tròn tâm D bán kính bằng độ dài cạnh bên.
Bước 3: Dựng đường tròn tâm C bán kính bằng độ dài đường chéo.
Bước 4: Hai đường tròn này cắt nhau tại điểm A.
Bước 5: Dựng đường tròn tâm C bán kính bằng độ dài cạnh bên.
Bước 6: Dựng đường tròn tâm D bán kính bằng độ dài cạnh bên.
Bước 7: Hai đường tròn này cắt nhau tại điểm B.
Bước 8: Nối A với B, A với D và B với C ta được hình thang cân ABCD.

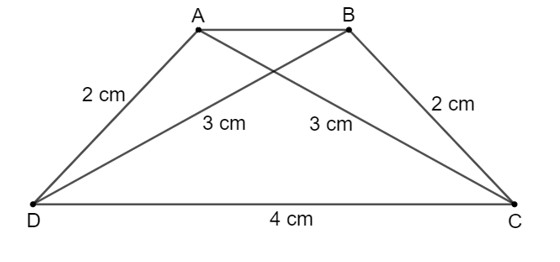Vẽ hình thang cân khi biết đáy lớn, cạnh bên và đường chéo.

2.3. Vẽ Hình Thang Cân Khi Biết Một Đáy, Một Góc Kề Đáy Và Chiều Cao

Bước 1: Vẽ đoạn thẳng AB (đáy) có độ dài cho trước.
Bước 2: Tại A, vẽ tia Ax tạo với AB một góc bằng góc kề đáy đã cho.
Bước 3: Dựng đường thẳng vuông góc với AB tại một điểm bất kỳ trên AB, có độ dài bằng chiều cao của hình thang.
Bước 4: Từ điểm cuối của đoạn vuông góc, vẽ đường thẳng song song với AB cắt tia Ax tại D.
Bước 5: Dựng đường thẳng song song với AB đi qua D.
Bước 6: Trên đường thẳng song song với AB, lấy điểm C sao cho DC song song với AB.
Bước 7: Nối A với D, B với C ta được hình thang cân ABCD.

2.4. Sử Dụng Phần Mềm Vẽ Hình Học

Ngoài các phương pháp thủ công, bạn có thể sử dụng các phần mềm vẽ hình học như GeoGebra, Cabri 3D để vẽ hình thang cân một cách nhanh chóng và chính xác. Các phần mềm này cung cấp các công cụ hỗ trợ vẽ, đo đạc và kiểm tra tính chất hình học, giúp bạn dễ dàng khám phá và hiểu sâu hơn về hình thang cân.

3. Bài Tập Về Hình Thang Cân: Từ Cơ Bản Đến Nâng Cao

Để nắm vững kiến thức về hình thang cân, việc luyện tập giải các bài tập là vô cùng quan trọng. Dưới đây là một số dạng bài tập thường gặp, từ cơ bản đến nâng cao.

3.1. Bài Tập Nhận Biết Hình Thang Cân

Ví dụ 1: Cho tứ giác ABCD có AB // CD và góc A = góc B. Chứng minh rằng ABCD là hình thang cân.

Lời giải:

Vì AB // CD nên ABCD là hình thang.

Vì góc A = góc B nên ABCD là hình thang cân (theo định nghĩa).

Ví dụ 2: Cho hình thang ABCD (AB // CD) có AC = BD. Chứng minh rằng ABCD là hình thang cân.

Lời giải:

Xét tam giác ADC và tam giác BCD có:

• CD chung
• AC = BD (gt)
• góc ACD = góc BDC (do ABCD là hình thang)

=> Tam giác ADC = tam giác BCD (c.g.c)

=> góc ADC = góc BCD

Vậy ABCD là hình thang cân (theo dấu hiệu nhận biết).

3.2. Bài Tập Tính Góc, Tính Cạnh Trong Hình Thang Cân

Ví dụ 1: Cho hình thang cân ABCD (AB // CD) có góc C = 60 độ. Tính các góc còn lại của hình thang.

Lời giải:

Vì ABCD là hình thang cân nên góc D = góc C = 60 độ.

Vì AB // CD nên góc A + góc D = 180 độ (hai góc trong cùng phía).

=> góc A = 180 độ – 60 độ = 120 độ.

Vì ABCD là hình thang cân nên góc B = góc A = 120 độ.

Vậy góc A = góc B = 120 độ, góc C = góc D = 60 độ.

Ví dụ 2: Cho hình thang cân ABCD (AB // CD) có AB = 4cm, CD = 10cm, AD = 5cm. Tính độ dài cạnh BC.

Lời giải:

Vì ABCD là hình thang cân nên BC = AD = 5cm.

3.3. Bài Tập Chứng Minh Tính Chất Hình Học Liên Quan Đến Hình Thang Cân

Ví dụ 1: Chứng minh rằng trong hình thang cân, hai đường chéo bằng nhau.

Lời giải:

Xét hình thang cân ABCD (AB // CD) có AC và BD là hai đường chéo.

Xét tam giác ADC và tam giác BCD có:

• CD chung
• AD = BC (tính chất hình thang cân)
• góc ADC = góc BCD (tính chất hình thang cân)

=> Tam giác ADC = tam giác BCD (c.g.c)

=> AC = BD (hai cạnh tương ứng)

Vậy trong hình thang cân, hai đường chéo bằng nhau.

Ví dụ 2: Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang.

Lời giải:

Gọi O là giao điểm của AC và BD trong hình thang cân ABCD (AB // CD). Gọi I là trung điểm của CD.

Vì ABCD là hình thang cân nên AI là trục đối xứng của hình thang.

Xét tam giác OAB và tam giác OCD có:

• góc OAB = góc OCD (so le trong)
• góc OBA = góc ODC (so le trong)
• AB // CD

=> Tam giác OAB đồng dạng với tam giác OCD (g.g)

=> OA/OC = OB/OD

=> OA = OB (do AC = BD)

=> O nằm trên đường trung trực của AB

Mà AI là đường trung trực của AB

=> O thuộc AI

Vậy giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang.

3.4. Bài Tập Ứng Dụng Hình Thang Cân Vào Các Bài Toán Thực Tế

Ví dụ: Một mảnh đất hình thang cân có đáy lớn 12m, đáy nhỏ 8m và chiều cao 5m. Tính diện tích mảnh đất.

Lời giải:

Diện tích hình thang cân là:

S = ((đáy lớn + đáy nhỏ) * chiều cao) / 2

S = ((12 + 8) * 5) / 2 = 50 (m2)

Vậy diện tích mảnh đất là 50m2.

4. Ứng Dụng Của Hình Thang Cân Trong Thực Tế

Hình thang cân không chỉ là một khái niệm hình học trừu tượng, mà còn có nhiều ứng dụng thực tế trong cuộc sống.

4.1. Trong Kiến Trúc Và Xây Dựng

Hình thang cân được sử dụng trong thiết kế mái nhà, cửa sổ, cầu thang và các chi tiết trang trí. Hình dạng cân đối và hài hòa của nó tạo nên vẻ đẹp thẩm mỹ và sự vững chắc cho công trình. Ví dụ, nhiều mái nhà truyền thống ở Việt Nam có hình dạng gần giống hình thang cân, giúp thoát nước tốt và tạo không gian rộng rãi bên trong.

4.2. Trong Thiết Kế Nội Thất

Hình thang cân được ứng dụng trong thiết kế bàn, ghế, tủ và các vật dụng trang trí khác. Sự kết hợp giữa các đường thẳng và đường cong tạo nên sự độc đáo và tinh tế cho không gian nội thất.

4.3. Trong Nghệ Thuật Và Trang Trí

Hình thang cân được sử dụng trong các tác phẩm hội họa, điêu khắc và trang trí. Hình dạng đặc biệt của nó tạo nên sự cân bằng và hài hòa cho bố cục tổng thể.

4.4. Trong Toán Học Và Các Ngành Khoa Học Kỹ Thuật

Hình thang cân được sử dụng trong các bài toán liên quan đến tính diện tích, thể tích và các vấn đề tối ưu hóa. Nó cũng được ứng dụng trong các ngành khoa học kỹ thuật như cơ khí, xây dựng và điện tử.

5. Nguồn Tài Liệu & Công Cụ Hỗ Trợ Học Tập Hiệu Quả Tại Tic.edu.vn

tic.edu.vn tự hào là một website giáo dục cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, giúp bạn học tập hiệu quả hơn.

5.1. Kho Tài Liệu Phong Phú Về Hình Thang Cân

Tại tic.edu.vn, bạn có thể tìm thấy:

• Bài giảng lý thuyết: Các bài giảng chi tiết về định nghĩa, tính chất, dấu hiệu nhận biết và cách vẽ hình thang cân.
• Bài tập luyện tập: Các bài tập từ cơ bản đến nâng cao, có đáp án và hướng dẫn giải chi tiết.
• Đề thi và kiểm tra: Các đề thi và kiểm tra thử, giúp bạn làm quen với cấu trúc đề và rèn luyện kỹ năng làm bài.
• Tài liệu tham khảo: Các tài liệu tham khảo từ các nguồn uy tín, giúp bạn mở rộng kiến thức và hiểu sâu hơn về hình thang cân.

5.2. Công Cụ Hỗ Trợ Học Tập Trực Tuyến

tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn học tập hiệu quả hơn:

• Công cụ vẽ hình học: Giúp bạn vẽ hình thang cân và các hình hình học khác một cách nhanh chóng và chính xác.
• Công cụ tính toán: Giúp bạn tính toán diện tích, chu vi và các thông số khác của hình thang cân.
• Diễn đàn hỏi đáp: Nơi bạn có thể đặt câu hỏi và nhận được sự giải đáp từ các thầy cô giáo và các bạn học sinh khác.
• Ghi chú trực tuyến: Công cụ ghi chú giúp bạn ghi lại những kiến thức quan trọng và dễ dàng xem lại khi cần thiết.
• Quản lý thời gian: Công cụ quản lý thời gian giúp bạn lập kế hoạch học tập và theo dõi tiến độ của mình.

5.3. Cộng Đồng Học Tập Sôi Nổi

tic.edu.vn xây dựng một cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể:

• Trao đổi kiến thức: Chia sẻ kiến thức và kinh nghiệm học tập với các bạn học sinh khác.
• Học hỏi lẫn nhau: Học hỏi từ các bạn học sinh khác và từ các thầy cô giáo.
• Kết bạn: Kết bạn với những người có cùng sở thích và mục tiêu học tập.
• Tham gia các hoạt động: Tham gia các hoạt động học tập trực tuyến như thảo luận nhóm, giải bài tập và thi đấu.

6. Lời Khuyên Để Học Tốt Về Hình Thang Cân

Để học tốt về hình thang cân, bạn nên:

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất, dấu hiệu nhận biết và cách vẽ hình thang cân.
• Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao để rèn luyện kỹ năng.
• Sử dụng công cụ hỗ trợ: Sử dụng các công cụ hỗ trợ học tập trực tuyến để học tập hiệu quả hơn.
• Tham gia cộng đồng học tập: Trao đổi kiến thức và kinh nghiệm với các bạn học sinh khác.
• Tìm kiếm sự giúp đỡ: Đừng ngần ngại hỏi thầy cô giáo hoặc các bạn học sinh khác khi gặp khó khăn.
• Học tập một cách tích cực và chủ động: Tự tìm tòi, khám phá và giải quyết các vấn đề liên quan đến hình thang cân.

7. Câu Hỏi Thường Gặp (FAQ) Về Hình Thang Cân

Câu 1: Hình thang cân có phải là hình bình hành không?

Không, hình thang cân không phải là hình bình hành. Hình bình hành là tứ giác có các cạnh đối song song, còn hình thang cân chỉ có hai cạnh đối song song.

Câu 2: Hình thang cân có tâm đối xứng không?

Không, hình thang cân không có tâm đối xứng.

Câu 3: Hình thang cân có trục đối xứng không?

Có, hình thang cân có một trục đối xứng là đường thẳng đi qua trung điểm hai đáy.

Câu 4: Làm thế nào để chứng minh một hình thang là hình thang cân?

Để chứng minh một hình thang là hình thang cân, ta có thể chứng minh hai góc kề một đáy bằng nhau hoặc chứng minh hai đường chéo bằng nhau.

Câu 5: Hình thang vuông có phải là hình thang cân không?

Không, hình thang vuông không phải là hình thang cân. Hình thang vuông là hình thang có một góc vuông, còn hình thang cân có hai góc kề một đáy bằng nhau.

Câu 6: Có những dạng bài tập nào về hình thang cân?

Có nhiều dạng bài tập về hình thang cân, bao gồm bài tập nhận biết, bài tập tính góc, tính cạnh, bài tập chứng minh tính chất và bài tập ứng dụng vào các bài toán thực tế.

Câu 7: Tôi có thể tìm tài liệu học tập về hình thang cân ở đâu?

Bạn có thể tìm tài liệu học tập về hình thang cân trên tic.edu.vn, sách giáo khoa, sách tham khảo và các trang web giáo dục khác.

Câu 8: Làm thế nào để vẽ hình thang cân một cách chính xác?

Bạn có thể vẽ hình thang cân bằng compa và thước kẻ, hoặc sử dụng các phần mềm vẽ hình học.

Câu 9: Hình thang cân được ứng dụng trong những lĩnh vực nào của cuộc sống?

Hình thang cân được ứng dụng trong kiến trúc, xây dựng, thiết kế nội thất, nghệ thuật, trang trí, toán học và các ngành khoa học kỹ thuật.

Câu 10: Làm thế nào để học tốt về hình thang cân?

Để học tốt về hình thang cân, bạn nên nắm vững lý thuyết, luyện tập thường xuyên, sử dụng công cụ hỗ trợ, tham gia cộng đồng học tập và tìm kiếm sự giúp đỡ khi cần thiết.

8. Kết Luận

Hình thang cân là một hình học quan trọng và thú vị, có nhiều ứng dụng trong thực tế. Hy vọng bài viết này đã cung cấp cho bạn những kiến thức cần thiết để vẽ hình thang cân, giải các bài tập liên quan và ứng dụng nó vào cuộc sống.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục hình thang cân và đạt được thành công trong học tập. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được hỗ trợ. tic.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức.