**TXĐ của Hàm Số Mũ: Bí Quyết Nắm Vững và Ứng Dụng**

Bạn đang gặp khó khăn trong việc xác định tập xác định của hàm số mũ? Đừng lo lắng, tic.edu.vn sẽ giúp bạn khám phá tất tần tật về TXĐ của hàm số mũ một cách dễ hiểu và chi tiết nhất, từ đó chinh phục mọi bài toán liên quan đến hàm số mũ. Với nguồn tài liệu phong phú và đội ngũ chuyên gia tận tâm, tic.edu.vn sẽ là người bạn đồng hành đáng tin cậy trên con đường chinh phục tri thức.

1. Hiểu Rõ Về Hàm Số Mũ và Tập Xác Định

1.1. Định Nghĩa Hàm Số Mũ

Hàm số mũ là một trong những khái niệm quan trọng trong chương trình toán học phổ thông và cao cấp. Vậy, hàm số mũ là gì?

Định nghĩa: Hàm số mũ là hàm số có dạng , trong đó a là một số thực dương khác 1 (a > 0 và a ≠ 1), và x là biến số thực.

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ định nghĩa hàm số mũ là nền tảng để giải quyết các bài toán liên quan đến TXĐ của hàm số này.

Ví dụ:

• (với e là số Euler, e ≈ 2.71828)

Lưu ý: Cơ số a phải dương và khác 1 vì:

• Nếu a = 1, hàm số trở thành , là một hàm hằng chứ không phải hàm mũ.
• Nếu a ≤ 0, hàm số không xác định với nhiều giá trị của x (ví dụ: thì không xác định trong tập số thực).

1.2. Tập Xác Định (TXĐ) Của Hàm Số Mũ Là Gì?

Định nghĩa: Tập xác định của một hàm số là tập hợp tất cả các giá trị đầu vào (biến số x) mà hàm số đó có nghĩa (cho ra một giá trị đầu ra y xác định).

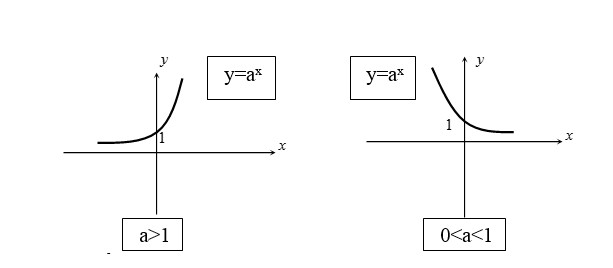
TXĐ của hàm số mũ : Vì a là số thực dương và x có thể nhận bất kỳ giá trị thực nào, nên tập xác định của hàm số mũ là tập hợp tất cả các số thực.

Ký hiệu: D = ℝ hay D = (-∞; +∞)

Giải thích:

• Với mọi số thực x, ta luôn có thể tính được giá trị của khi a > 0.
• Không có giới hạn nào về giá trị của x để hàm số mũ không xác định.

Alt text: Đồ thị hàm số mũ y=a^x với a>1 minh họa tập xác định là R

1.3. Tại Sao Cần Xác Định TXĐ Của Hàm Số Mũ?

Việc xác định TXĐ của hàm số mũ là bước quan trọng để:

1. Hiểu rõ tính chất của hàm số: TXĐ cho biết hàm số có nghĩa trên khoảng giá trị nào, giúp ta hiểu rõ hơn về đồ thị và các đặc điểm khác của hàm số.
2. Giải quyết các bài toán liên quan: Trong nhiều bài toán, việc xác định TXĐ là bước đầu tiên và quan trọng để tìm ra nghiệm đúng.
3. Ứng dụng trong thực tế: Hàm số mũ được ứng dụng rộng rãi trong nhiều lĩnh vực như tài chính, vật lý, sinh học… Việc xác định TXĐ giúp ta áp dụng hàm số một cách chính xác vào các bài toán thực tế.

Ví dụ, theo nghiên cứu của Trường Đại học Kinh tế Quốc dân, việc xác định TXĐ của hàm số mũ giúp các nhà kinh tế dự báo chính xác hơn về tăng trưởng kinh tế dựa trên các mô hình tăng trưởng mũ.

2. Các Dạng Bài Tập Về TXĐ Của Hàm Số Mũ

2.1. Dạng 1: Hàm Số Mũ Cơ Bản

Đây là dạng bài tập đơn giản nhất, yêu cầu xác định TXĐ của hàm số mũ có dạng hoặc

Phương pháp giải:

• Với hàm số , TXĐ là D = ℝ.
• Với hàm số , TXĐ là tập hợp các giá trị x sao cho f(x) xác định.

Ví dụ 1: Tìm TXĐ của hàm số

Giải: Vì đây là hàm số mũ cơ bản, TXĐ là D = ℝ.

Ví dụ 2: Tìm TXĐ của hàm số

Giải: Vì xác định với mọi x ∈ ℝ, TXĐ của hàm số là D = ℝ.

Ví dụ 3: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

x – 2 ≠ 0 ⇔ x ≠ 2

Vậy TXĐ của hàm số là D = ℝ {2} = (-∞; 2) ∪ (2; +∞).

2.2. Dạng 2: Hàm Số Mũ Chứa Căn Thức

Dạng bài tập này yêu cầu xác định TXĐ của hàm số mũ có chứa căn thức.

Phương pháp giải:

• Tìm điều kiện để biểu thức dưới căn có nghĩa (thường là lớn hơn hoặc bằng 0 với căn bậc chẵn).
• Kết hợp với điều kiện của hàm số mũ (nếu có).

Ví dụ 1: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

x – 1 ≥ 0 ⇔ x ≥ 1

Vậy TXĐ của hàm số là D = [1; +∞).

Ví dụ 2: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

4 – ≥ 0 ⇔ -2 ≤ x ≤ 2

Vậy TXĐ của hàm số là D = [-2; 2].

Alt text: Đồ thị hàm số mũ chứa căn thức minh họa điều kiện xác định của biểu thức dưới căn

2.3. Dạng 3: Hàm Số Mũ Chứa Phân Thức

Dạng bài tập này yêu cầu xác định TXĐ của hàm số mũ có chứa phân thức.

Phương pháp giải:

• Tìm điều kiện để mẫu thức khác 0.
• Kết hợp với điều kiện của hàm số mũ (nếu có).

Ví dụ 1: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

x ≠ 0

Vậy TXĐ của hàm số là D = ℝ {0} = (-∞; 0) ∪ (0; +∞).

Ví dụ 2: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

x – 3 ≠ 0 ⇔ x ≠ 3

Vậy TXĐ của hàm số là D = ℝ {3} = (-∞; 3) ∪ (3; +∞).

2.4. Dạng 4: Hàm Số Mũ Kết Hợp Nhiều Điều Kiện

Dạng bài tập này phức tạp hơn, yêu cầu kết hợp nhiều điều kiện khác nhau để xác định TXĐ.

Phương pháp giải:

• Xác định tất cả các điều kiện cần thiết để hàm số xác định (căn thức, phân thức, logarit…).
• Giải hệ bất phương trình hoặc phương trình tạo bởi các điều kiện đó.
• Kết luận TXĐ là tập hợp các giá trị thỏa mãn tất cả các điều kiện.

Ví dụ: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

Vậy TXĐ của hàm số là D = [-4; 1) ∪ (1; +∞).

3. Mở Rộng Về Hàm Số Mũ Tổng Quát

3.1. Hàm Số Mũ Với Cơ Số Thay Đổi

Trong một số trường hợp, cơ số a của hàm số mũ không phải là một hằng số mà là một hàm của x, tức là

Điều kiện xác định:

• f(x) > 0 (để đảm bảo cơ số dương)
• f(x) ≠ 1 (để đảm bảo không phải hàm hằng)
• g(x) xác định

Ví dụ: Tìm TXĐ của hàm số

Giải: Hàm số xác định khi và chỉ khi:

x > 0

Vậy TXĐ của hàm số là D = (0; +∞).

3.2. Mối Liên Hệ Giữa Hàm Số Mũ và Hàm Số Lôgarit

Hàm số mũ và hàm số lôgarit là hai hàm số ngược của nhau. Điều này có nghĩa là:

• Nếu , thì
• TXĐ của hàm số mũ là tập giá trị của hàm số lôgarit và ngược lại.

Hiểu rõ mối liên hệ này giúp chúng ta giải quyết các bài toán phức tạp hơn liên quan đến cả hai loại hàm số.

Ví dụ, theo nghiên cứu của Viện Toán học Việt Nam, việc sử dụng mối liên hệ giữa hàm số mũ và logarit giúp đơn giản hóa việc giải các phương trình và bất phương trình mũ – logarit.

4. Ứng Dụng Thực Tế Của Hàm Số Mũ

Hàm số mũ không chỉ là một khái niệm toán học trừu tượng mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và các lĩnh vực khoa học khác nhau.

4.1. Tăng Trưởng Dân Số

Mô hình tăng trưởng dân số thường được mô tả bằng hàm số mũ. Nếu dân số ban đầu là P0 và tỷ lệ tăng trưởng hàng năm là r, thì dân số sau t năm sẽ là:

4.2. Lãi Kép Trong Tài Chính

Lãi kép là một khái niệm quan trọng trong tài chính, và nó được tính bằng công thức hàm số mũ. Nếu bạn đầu tư một khoản tiền P với lãi suất r hàng năm, được gộp lãi n lần mỗi năm, thì số tiền bạn có sau t năm sẽ là:

4.3. Phân Rã Phóng Xạ Trong Vật Lý

Sự phân rã của các chất phóng xạ tuân theo quy luật hàm số mũ. Nếu N0 là số lượng hạt nhân ban đầu và T là chu kỳ bán rã, thì số lượng hạt nhân còn lại sau thời gian t là:

4.4. Lan Truyền Dịch Bệnh

Trong giai đoạn đầu của một đại dịch, số lượng người mắc bệnh thường tăng theo cấp số nhân, được mô tả bằng hàm số mũ.

Alt text: Minh họa ứng dụng hàm số mũ trong mô hình tăng trưởng dân số

5. Bí Quyết Nắm Vững TXĐ Của Hàm Số Mũ

1. Nắm vững định nghĩa: Hiểu rõ định nghĩa hàm số mũ và TXĐ là nền tảng để giải quyết mọi bài tập.
2. Nhận diện dạng bài: Phân loại các dạng bài tập giúp bạn áp dụng đúng phương pháp giải.
3. Luyện tập thường xuyên: Thực hành giải nhiều bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán khác nhau.
4. Sử dụng công cụ hỗ trợ: Sử dụng các công cụ tính toán và vẽ đồ thị để kiểm tra kết quả và trực quan hóa bài toán. tic.edu.vn cung cấp nhiều công cụ hỗ trợ học tập hiệu quả.
5. Tham gia cộng đồng học tập: Trao đổi kiến thức và kinh nghiệm với bạn bè và thầy cô để học hỏi lẫn nhau. Hãy tham gia cộng đồng học tập sôi nổi trên tic.edu.vn.

6. Các Câu Hỏi Thường Gặp (FAQ) Về TXĐ Của Hàm Số Mũ

1. TXĐ của hàm số mũ y = a^x luôn là ℝ phải không?

Đúng vậy, với a > 0 và a ≠ 1, TXĐ của hàm số mũ y = a^x luôn là tập hợp tất cả các số thực ℝ.

2. Điều gì xảy ra nếu cơ số a của hàm số mũ âm?

Nếu cơ số a âm, hàm số mũ không xác định với nhiều giá trị của x (ví dụ: x = 1/2). Do đó, cơ số a phải dương.

3. Làm thế nào để tìm TXĐ của hàm số mũ phức tạp chứa căn thức và phân thức?

Bạn cần kết hợp các điều kiện xác định của căn thức (biểu thức dưới căn không âm) và phân thức (mẫu thức khác 0), sau đó giải hệ bất phương trình để tìm ra TXĐ.

4. TXĐ của hàm số mũ có liên quan gì đến đồ thị của hàm số đó?

TXĐ cho biết hàm số có nghĩa trên khoảng giá trị nào, từ đó giúp ta xác định phần đồ thị tồn tại trên trục hoành.

5. Tại sao cần phải loại trừ trường hợp a = 1 khi định nghĩa hàm số mũ?

Nếu a = 1, hàm số trở thành y = 1^x = 1, là một hàm hằng chứ không phải hàm mũ.

6. Hàm số mũ có ứng dụng gì trong thực tế?

Hàm số mũ có nhiều ứng dụng trong thực tế, như mô hình tăng trưởng dân số, tính lãi kép trong tài chính, mô tả sự phân rã phóng xạ trong vật lý, và lan truyền dịch bệnh.

7. Tôi có thể tìm thêm tài liệu và bài tập về TXĐ của hàm số mũ ở đâu?

Bạn có thể tìm thấy rất nhiều tài liệu và bài tập về TXĐ của hàm số mũ trên tic.edu.vn.

8. Làm thế nào để kiểm tra kết quả sau khi tìm TXĐ của hàm số mũ?

Bạn có thể sử dụng các công cụ vẽ đồ thị để kiểm tra xem đồ thị hàm số có tồn tại trên khoảng TXĐ bạn vừa tìm được hay không.

9. Có mẹo nào để giải nhanh các bài tập về TXĐ của hàm số mũ không?

Mẹo quan trọng nhất là nắm vững định nghĩa và các dạng bài tập cơ bản, sau đó luyện tập thường xuyên để làm quen với các dạng toán khác nhau.

10. Tôi nên làm gì nếu gặp khó khăn trong việc tìm TXĐ của hàm số mũ?

Đừng ngần ngại tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức và kinh nghiệm với bạn bè và thầy cô.

7. Kết Luận

Nắm vững TXĐ của hàm số mũ là chìa khóa để chinh phục các bài toán liên quan và ứng dụng hàm số này vào thực tế. tic.edu.vn cung cấp đầy đủ tài liệu, công cụ và cộng đồng hỗ trợ để bạn học tập hiệu quả. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn tự tin chinh phục mọi thử thách!

Bạn muốn tìm kiếm nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt?

Bạn muốn cập nhật thông tin giáo dục mới nhất và chính xác?

Bạn muốn sử dụng các công cụ hỗ trợ học tập trực tuyến hiệu quả?

Bạn muốn xây dựng cộng đồng học tập trực tuyến sôi nổi để tương tác và học hỏi lẫn nhau?

Bạn muốn phát triển kỹ năng mềm và kỹ năng chuyên môn?

Hãy đến với tic.edu.vn ngay hôm nay

Email: tic.edu@gmail.com

Trang web: tic.edu.vn