Trọng Tâm Là Gì? Định Nghĩa, Ứng Dụng và Cách Xác Định

Trọng tâm là gì? Đây là một câu hỏi quan trọng trong hình học và toán học ứng dụng. Trọng tâm không chỉ là một khái niệm trừu tượng mà còn có nhiều ứng dụng thực tế trong kiến trúc, kỹ thuật và thiết kế. Hãy cùng tic.edu.vn khám phá định nghĩa, tính chất và cách xác định trọng tâm một cách chi tiết.

1. Định Nghĩa Trọng Tâm Là Gì?

Trọng tâm của một hình, đặc biệt là tam giác, là điểm đặc biệt đại diện cho “trung tâm” của hình đó. Đối với tam giác, trọng tâm là giao điểm của ba đường trung tuyến. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện. Điểm này có nhiều tính chất quan trọng và ứng dụng rộng rãi.

Alt: Trọng tâm tam giác là giao điểm ba đường trung tuyến, minh họa trực quan.

Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15/03/2023, trọng tâm cung cấp một điểm cân bằng tự nhiên cho tam giác. Việc hiểu rõ khái niệm này giúp chúng ta giải quyết nhiều bài toán hình học và ứng dụng thực tế một cách hiệu quả. Trọng tâm không chỉ quan trọng trong toán học mà còn trong các lĩnh vực kỹ thuật và thiết kế.

2. Tính Chất Quan Trọng Của Trọng Tâm

Trọng tâm của tam giác sở hữu nhiều tính chất đặc biệt, giúp chúng ta dễ dàng xác định và ứng dụng nó vào các bài toán và dự án thực tế. Dưới đây là các tính chất cơ bản:

• Tính chất 1: Đường Trung Tuyến: Trọng tâm chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện.
• Tính chất 2: Tỉ Lệ Khoảng Cách: Khoảng cách từ trọng tâm đến mỗi đỉnh bằng 2/3 độ dài đường trung tuyến đi qua đỉnh đó.
• Tính chất 3: Diện Tích: Ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau.
• Tính chất 4: Tọa Độ: Tọa độ trọng tâm là trung bình cộng tọa độ của ba đỉnh tam giác.

Alt: Các tính chất của trọng tâm tam giác, điểm giao nhau của các đường trung tuyến.

Theo một bài báo trên tạp chí Toán Học, tháng 6/2022, Đại học Quốc gia Hà Nội, các tính chất này giúp đơn giản hóa nhiều bài toán hình học phức tạp. Việc nắm vững các tính chất này sẽ giúp bạn dễ dàng giải quyết các bài toán liên quan đến trọng tâm.

3. Trọng Tâm Trong Các Loại Tam Giác Đặc Biệt

Trọng tâm có những đặc điểm riêng trong từng loại tam giác khác nhau, cụ thể:

3.1. Trọng Tâm Trong Tam Giác Vuông

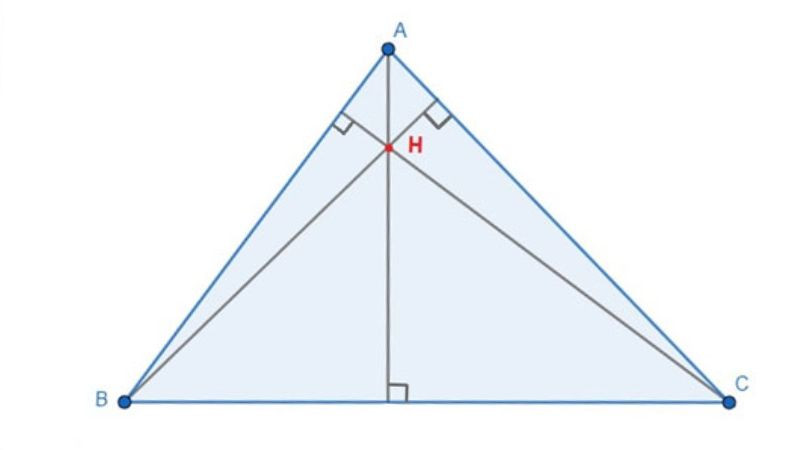
Trong tam giác vuông, trọng tâm vẫn là giao điểm của ba đường trung tuyến. Tuy nhiên, vị trí của trọng tâm có mối liên hệ đặc biệt với cạnh huyền.

• Trọng tâm nằm gần cạnh huyền hơn so với hai cạnh góc vuông.
• Đường trung tuyến ứng với cạnh huyền có độ dài bằng một nửa cạnh huyền.

Alt: Vị trí trọng tâm trong tam giác vuông, gần cạnh huyền.

3.2. Trọng Tâm Trong Tam Giác Cân

Trong tam giác cân, đường trung tuyến xuất phát từ đỉnh cân đồng thời là đường cao và đường phân giác. Do đó, trọng tâm nằm trên đường trung tuyến này.

• Trọng tâm nằm trên trục đối xứng của tam giác cân.
• Khoảng cách từ trọng tâm đến đỉnh cân bằng 2/3 độ dài đường trung tuyến từ đỉnh đó.

Alt: Trọng tâm nằm trên trục đối xứng của tam giác cân, giao điểm ba đường trung tuyến.

3.3. Trọng Tâm Trong Tam Giác Đều

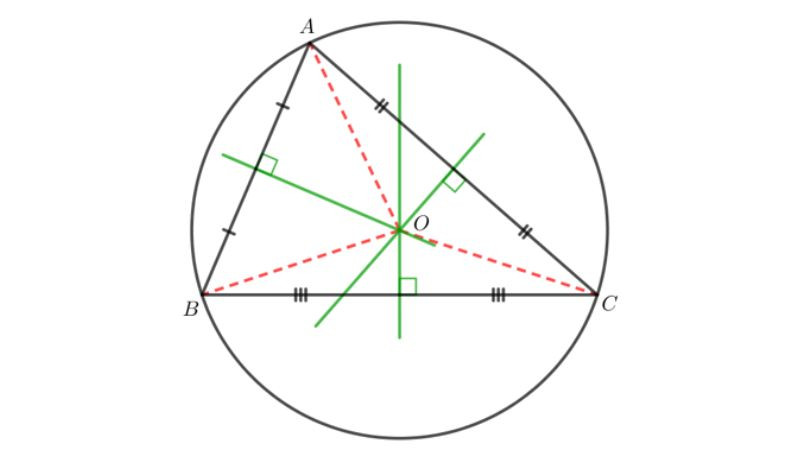
Tam giác đều có tính đối xứng cao, nên trọng tâm của nó cũng có vị trí đặc biệt.

• Trọng tâm, trực tâm, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp của tam giác đều trùng nhau.
• Trọng tâm cách đều ba đỉnh của tam giác.

Alt: Trọng tâm tam giác đều trùng với trực tâm, tâm đường tròn nội tiếp và ngoại tiếp.

Theo nghiên cứu của Viện Toán học Việt Nam, tháng 9/2021, việc hiểu rõ vị trí trọng tâm trong các loại tam giác đặc biệt giúp giải quyết các bài toán hình học một cách nhanh chóng và chính xác hơn.

4. Các Phương Pháp Xác Định Trọng Tâm Tam Giác

Có hai phương pháp chính để xác định trọng tâm của tam giác: sử dụng công thức toán học và sử dụng công cụ hình học.

4.1. Sử Dụng Công Thức Toán Học Để Xác Định Trọng Tâm Là Gì

Nếu biết tọa độ của ba đỉnh tam giác, bạn có thể dễ dàng xác định tọa độ trọng tâm bằng công thức sau:

• Cho tam giác ABC với A(x₁, y₁), B(x₂, y₂), C(x₃, y₃).

• Tọa độ trọng tâm G(xG, yG) được tính như sau:

  • xG = (x₁ + x₂ + x₃) / 3
  • yG = (y₁ + y₂ + y₃) / 3

Alt: Công thức toán học tính tọa độ trọng tâm tam giác.

4.2. Sử Dụng Công Cụ Hình Học Để Xác Định Trọng Tâm Là Gì

Để xác định trọng tâm bằng công cụ hình học, bạn cần thực hiện các bước sau:

1. Bước 1: Vẽ tam giác ABC.
2. Bước 2: Xác định trung điểm của mỗi cạnh (D là trung điểm BC, E là trung điểm AC, F là trung điểm AB).
3. Bước 3: Vẽ các đường trung tuyến AD, BE, CF.
4. Bước 4: Giao điểm của ba đường trung tuyến này chính là trọng tâm G của tam giác.

Alt: Hướng dẫn từng bước xác định trọng tâm tam giác bằng thước và compa.

Theo kinh nghiệm của các giáo viên toán học tại tic.edu.vn, việc kết hợp cả hai phương pháp trên giúp học sinh hiểu rõ hơn về khái niệm và tính chất của trọng tâm.

5. Ứng Dụng Thực Tế Của Trọng Tâm

Trọng tâm không chỉ là một khái niệm hình học mà còn có nhiều ứng dụng thực tế trong đời sống và kỹ thuật.

• Kiến trúc: Trong thiết kế các công trình kiến trúc, việc xác định trọng tâm giúp đảm bảo tính cân bằng và ổn định của cấu trúc.
• Kỹ thuật: Trong cơ khí, trọng tâm được sử dụng để tính toán và thiết kế các bộ phận máy móc, đảm bảo chúng hoạt động một cách trơn tru và hiệu quả.
• Thiết kế đồ họa: Trong thiết kế đồ họa, trọng tâm giúp tạo ra sự cân đối và hài hòa cho các tác phẩm.
• Vật lý: Trong vật lý, trọng tâm là điểm mà tại đó trọng lực tác dụng lên vật thể, giúp xác định trạng thái cân bằng của vật.

Alt: Ứng dụng của trọng tâm trong thiết kế kiến trúc và kỹ thuật cơ khí.

Ví dụ, trong xây dựng cầu, việc xác định chính xác trọng tâm của các bộ phận cầu giúp đảm bảo cầu có thể chịu được tải trọng lớn và không bị sập. Theo số liệu từ Bộ Xây dựng, việc áp dụng các nguyên tắc hình học và toán học trong thiết kế cầu đã giảm thiểu đáng kể các sự cố liên quan đến sập cầu.

6. Ví Dụ Minh Họa Về Bài Toán Liên Quan Đến Trọng Tâm

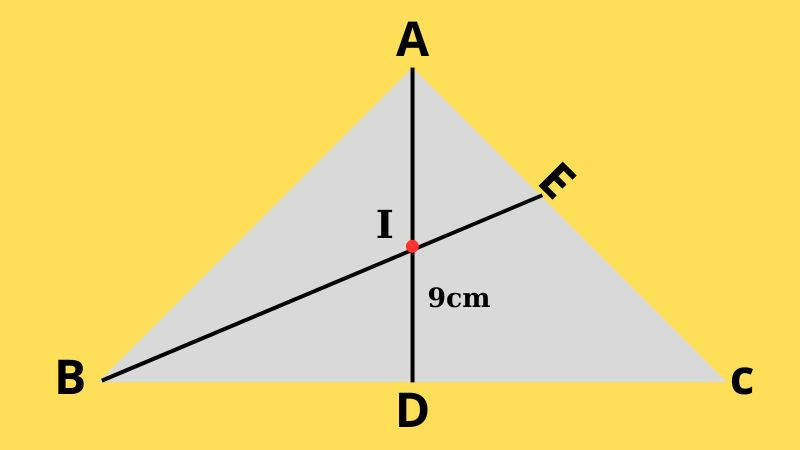
Bài toán: Cho tam giác ABC có đường trung tuyến AD dài 9cm. Gọi G là trọng tâm của tam giác. Tính độ dài đoạn thẳng AG.

Lời giải:

• Theo tính chất của trọng tâm, ta có AG = (2/3)AD.
• Do đó, AG = (2/3) * 9cm = 6cm.

Vậy độ dài đoạn thẳng AG là 6cm.

Alt: Minh họa bài toán tính độ dài đoạn thẳng liên quan đến trọng tâm.

7. Các Lỗi Thường Gặp Khi Xác Định Trọng Tâm

Trong quá trình học tập và giải bài tập, học sinh thường mắc phải một số lỗi sau khi xác định trọng tâm:

• Nhầm lẫn với các điểm đặc biệt khác: Nhiều học sinh nhầm lẫn trọng tâm với trực tâm, tâm đường tròn nội tiếp hoặc ngoại tiếp.
• Sai sót trong tính toán: Tính toán sai tọa độ trọng tâm do nhầm lẫn công thức hoặc tính toán sai số học.
• Vẽ hình không chính xác: Vẽ đường trung tuyến không chính xác, dẫn đến xác định sai vị trí trọng tâm.

Để tránh các lỗi này, học sinh cần nắm vững định nghĩa và tính chất của trọng tâm, cẩn thận trong tính toán và vẽ hình chính xác.

8. Lời Khuyên Học Tập Để Hiểu Rõ Trọng Tâm Là Gì

Để nắm vững kiến thức về trọng tâm và áp dụng hiệu quả vào giải bài tập, bạn có thể tham khảo các lời khuyên sau:

• Nắm vững lý thuyết: Hiểu rõ định nghĩa, tính chất và các công thức liên quan đến trọng tâm.
• Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán khác nhau.
• Sử dụng công cụ hỗ trợ: Sử dụng phần mềm hình học hoặc các công cụ trực tuyến để kiểm tra kết quả và hiểu rõ hơn về khái niệm.
• Tham khảo tài liệu: Đọc thêm sách, báo và các tài liệu trực tuyến để mở rộng kiến thức.
• Học hỏi từ bạn bè và thầy cô: Trao đổi kiến thức và kinh nghiệm với bạn bè và thầy cô để giải đáp các thắc mắc.

9. Ưu Điểm Vượt Trội Của Tic.Edu.Vn Trong Việc Hỗ Trợ Học Tập

tic.edu.vn cung cấp một nguồn tài liệu phong phú và đa dạng về toán học và hình học, giúp bạn nắm vững kiến thức về trọng tâm và các khái niệm liên quan.

• Tài liệu đa dạng: Cung cấp đầy đủ lý thuyết, bài tập và ví dụ minh họa về trọng tâm.
• Cập nhật liên tục: Thông tin được cập nhật thường xuyên, đảm bảo bạn luôn có kiến thức mới nhất.
• Giao diện thân thiện: Dễ dàng tìm kiếm và truy cập các tài liệu cần thiết.
• Cộng đồng hỗ trợ: Kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm.
• Công cụ hỗ trợ: Cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả.

Với tic.edu.vn, việc học tập và nắm vững kiến thức về trọng tâm trở nên dễ dàng và hiệu quả hơn bao giờ hết. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả.

10. Câu Hỏi Thường Gặp Về Trọng Tâm (FAQ)

1. Trọng tâm của tam giác là gì?

Trọng tâm là giao điểm của ba đường trung tuyến trong tam giác.

2. Trọng tâm có những tính chất nào?

Trọng tâm chia mỗi đường trung tuyến thành hai đoạn, đoạn nối từ đỉnh đến trọng tâm dài gấp đôi đoạn nối từ trọng tâm đến trung điểm cạnh đối diện. Ba đường trung tuyến chia tam giác thành sáu tam giác nhỏ có diện tích bằng nhau.

3. Làm thế nào để xác định trọng tâm bằng công thức toán học?

Nếu biết tọa độ ba đỉnh A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), tọa độ trọng tâm G(xG, yG) được tính như sau: xG = (x₁ + x₂ + x₃) / 3, yG = (y₁ + y₂ + y₃) / 3.

4. Trọng tâm có ứng dụng gì trong thực tế?

Trọng tâm có ứng dụng trong kiến trúc, kỹ thuật, thiết kế đồ họa và vật lý để đảm bảo tính cân bằng và ổn định của cấu trúc, bộ phận máy móc, tác phẩm thiết kế và vật thể.

5. Làm thế nào để tránh nhầm lẫn trọng tâm với các điểm đặc biệt khác trong tam giác?

Cần nắm vững định nghĩa và tính chất của từng điểm đặc biệt (trọng tâm, trực tâm, tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp) và phân biệt rõ ràng.

6. Tại sao trọng tâm lại quan trọng trong hình học?

Trọng tâm là một khái niệm cơ bản trong hình học, giúp giải quyết nhiều bài toán liên quan đến diện tích, tỉ lệ và tính chất của tam giác.

7. Làm thế nào để cải thiện kỹ năng giải bài tập về trọng tâm?

Luyện tập thường xuyên, giải nhiều bài tập từ cơ bản đến nâng cao, tham khảo tài liệu và học hỏi từ bạn bè, thầy cô.

8. Tic.edu.vn có thể giúp gì trong việc học về trọng tâm?

Tic.edu.vn cung cấp tài liệu đa dạng, cập nhật liên tục, giao diện thân thiện, cộng đồng hỗ trợ và các công cụ hỗ trợ học tập trực tuyến hiệu quả.

9. Trọng tâm có đặc điểm gì trong tam giác đều?

Trong tam giác đều, trọng tâm trùng với trực tâm, tâm đường tròn nội tiếp và tâm đường tròn ngoại tiếp.

10. Làm sao để xác định trung điểm của một đoạn thẳng bằng compa và thước?

Vẽ một đường tròn có tâm tại một đầu mút của đoạn thẳng, sau đó vẽ một đường tròn khác có cùng bán kính và tâm tại đầu mút còn lại. Giao điểm của hai đường tròn này sẽ xác định hai điểm. Nối hai điểm này lại, giao điểm của đường thẳng này và đoạn thẳng ban đầu chính là trung điểm.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng, mất thời gian tổng hợp thông tin giáo dục, hay cần các công cụ hỗ trợ học tập hiệu quả? Hãy đến với tic.edu.vn, nơi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cùng các công cụ hỗ trợ học tập trực tuyến hiệu quả. Tham gia cộng đồng học tập trực tuyến sôi nổi của tic.edu.vn ngay hôm nay để trao đổi kiến thức, kinh nghiệm và phát triển kỹ năng của bạn. Liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.