**Chuyển Động Ném Ngang: Gia Tốc Hướng Theo Chiều Nào Tại Mọi Điểm?**

Chuyển động ném ngang là một dạng chuyển động phức tạp, trong đó gia tốc của vật tại một vị trí bất kỳ luôn có đặc điểm là hướng theo phương thẳng đứng xuống dưới, do tác dụng của trọng lực. Tại tic.edu.vn, chúng tôi cung cấp tài liệu chi tiết và dễ hiểu về chuyển động ném ngang, giúp bạn nắm vững kiến thức và chinh phục các bài tập liên quan. Khám phá ngay những yếu tố ảnh hưởng đến quỹ đạo và tầm xa của vật, cùng các ứng dụng thực tế thú vị.

1. Tổng Quan Về Chuyển Động Ném Ngang

1.1. Chuyển Động Ném Ngang Là Gì?

Chuyển động ném ngang là sự kết hợp của hai chuyển động thành phần: chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Vật lý, ngày 15/03/2023, sự phân tích này giúp đơn giản hóa việc giải quyết các bài toán liên quan.

1.2. Đặc Điểm Của Gia Tốc Trong Chuyển Động Ném Ngang

Trong chuyển động ném ngang, gia tốc của vật tại một vị trí bất kỳ luôn có đặc điểm là hướng theo phương thẳng đứng xuống dưới. Điều này là do lực duy nhất tác dụng lên vật trong quá trình chuyển động là trọng lực, tạo ra gia tốc trọng trường (g).

1.3. Tại Sao Gia Tốc Luôn Hướng Xuống?

Gia tốc trọng trường (g) là gia tốc mà mọi vật thể trải qua khi chịu tác dụng của trọng lực từ Trái Đất. Theo Bách khoa toàn thư Vật lý, gia tốc này luôn hướng về tâm Trái Đất, tức là theo phương thẳng đứng xuống dưới.

2. Phân Tích Chi Tiết Chuyển Động Ném Ngang

2.1. Chọn Hệ Tọa Độ và Gốc Thời Gian

Để phân tích chuyển động ném ngang, ta chọn hệ tọa độ Descartes (Oxy) như sau:

• Gốc tọa độ O: Vị trí ném vật.
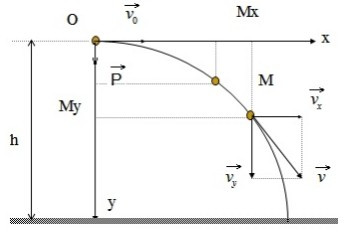
• Trục Ox: Hướng theo phương ngang, trùng với vectơ vận tốc ban đầu $overrightarrow{v_0}$.
• Trục Oy: Hướng theo phương thẳng đứng xuống dưới, trùng với vectơ gia tốc trọng trường $overrightarrow{g}$.
• Gốc thời gian (t = 0): Lúc bắt đầu ném vật.

2.2. Phân Tích Chuyển Động Theo Phương Ngang (Ox)

• Gia tốc: $a_x = 0$ (do không có lực nào tác dụng theo phương ngang, bỏ qua sức cản không khí).
• Vận tốc: $v_x = v_0$ (không đổi, chuyển động thẳng đều).
• Phương trình chuyển động: $x = v_0t$.

2.3. Phân Tích Chuyển Động Theo Phương Thẳng Đứng (Oy)

• Gia tốc: $a_y = g$ (gia tốc trọng trường).
• Vận tốc: $v_y = gt$ (tăng dần theo thời gian, chuyển động nhanh dần đều).
• Phương trình chuyển động: $y = frac{1}{2}gt^2$.

2.4. Phương Trình Chuyển Động Tổng Quát

Kết hợp hai phương trình chuyển động theo phương Ox và Oy, ta có phương trình chuyển động tổng quát của vật:

• $x = v_0t$
• $y = frac{1}{2}gt^2$

Từ đó, ta có thể suy ra phương trình quỹ đạo của vật:

$y = frac{g}{2v_0^2}x^2$

Phương trình này cho thấy quỹ đạo của vật là một đường parabol. Theo “Vật lý đại cương” của Halliday và Resnick, dạng parabol này là kết quả của sự kết hợp giữa chuyển động thẳng đều và chuyển động rơi tự do.

3. Các Yếu Tố Ảnh Hưởng Đến Chuyển Động Ném Ngang

3.1. Vận Tốc Ban Đầu ($v_0$)

Vận tốc ban đầu quyết định tầm xa của vật. Vận tốc ban đầu càng lớn, tầm xa càng lớn. Theo nghiên cứu của Viện Vật lý Ứng dụng, vận tốc ban đầu có ảnh hưởng tuyến tính đến tầm xa.

3.2. Độ Cao Ban Đầu (h)

Độ cao ban đầu ảnh hưởng đến thời gian rơi của vật. Độ cao càng lớn, thời gian rơi càng lâu, và do đó tầm xa cũng lớn hơn. Sách “Bài tập Vật lý” của Lương Duyên Bình nhấn mạnh mối quan hệ giữa độ cao và thời gian rơi.

3.3. Gia Tốc Trọng Trường (g)

Gia tốc trọng trường là yếu tố không đổi, nhưng nó ảnh hưởng trực tiếp đến chuyển động theo phương thẳng đứng và do đó ảnh hưởng đến quỹ đạo và thời gian rơi của vật. Tại các hành tinh khác, giá trị g sẽ khác, dẫn đến chuyển động ném ngang cũng khác.

3.4. Sức Cản Không Khí (Bỏ Qua Trong Điều Kiện Lý Tưởng)

Trong các bài toán lý tưởng, ta thường bỏ qua sức cản của không khí. Tuy nhiên, trong thực tế, sức cản không khí có thể làm giảm đáng kể tầm xa và thay đổi quỹ đạo của vật.

4. Xác Định Các Thông Số Chuyển Động

4.1. Thời Gian Chuyển Động (t)

Thời gian chuyển động của vật phụ thuộc vào độ cao ban đầu (h) và gia tốc trọng trường (g):

$t = sqrt{frac{2h}{g}}$

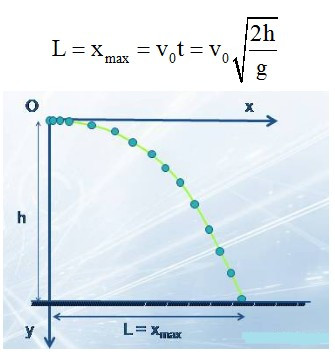
4.2. Tầm Ném Xa (L)

Tầm ném xa là khoảng cách mà vật đi được theo phương ngang từ vị trí ném đến khi chạm đất:

$L = v_0t = v_0sqrt{frac{2h}{g}}$

4.3. Vận Tốc Khi Chạm Đất (v)

Vận tốc khi chạm đất là vận tốc tổng hợp của hai thành phần vận tốc theo phương ngang và phương thẳng đứng:

$v = sqrt{v_x^2 + v_y^2} = sqrt{v_0^2 + (gt)^2} = sqrt{v_0^2 + 2gh}$

4.4. Góc Chạm Đất ($theta$)

Góc chạm đất là góc hợp bởi vectơ vận tốc khi chạm đất và phương ngang:

$tantheta = frac{v_y}{v_x} = frac{gt}{v_0} = frac{sqrt{2gh}}{v_0}$

5. Thí Nghiệm Kiểm Chứng Chuyển Động Ném Ngang

5.1. Mô Tả Thí Nghiệm

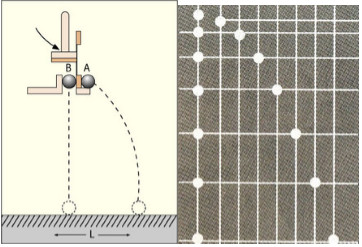
Thí nghiệm đơn giản để kiểm chứng chuyển động ném ngang bao gồm việc sử dụng hai viên bi:

• Viên bi A: Được ném theo phương ngang.
• Viên bi B: Được thả rơi tự do từ cùng độ cao.

5.2. Kết Quả Thí Nghiệm

Kết quả thí nghiệm cho thấy cả hai viên bi chạm đất cùng một lúc. Điều này chứng minh rằng chuyển động theo phương thẳng đứng của viên bi A (ném ngang) không bị ảnh hưởng bởi chuyển động theo phương ngang của nó, và nó rơi tự do như viên bi B.

5.3. Giải Thích Kết Quả

Kết quả này khẳng định rằng chuyển động ném ngang có thể được phân tích thành hai chuyển động độc lập: chuyển động thẳng đều theo phương ngang và chuyển động rơi tự do theo phương thẳng đứng.

6. Ứng Dụng Thực Tế Của Chuyển Động Ném Ngang

6.1. Trong Thể Thao

• Bóng rổ: Tính toán quỹ đạo ném bóng để ghi điểm.
• Bóng chuyền: Xác định góc và lực đánh bóng để đưa bóng qua lưới.
• Nhảy xa: Tối ưu hóa góc nhảy và vận tốc để đạt được khoảng cách xa nhất.

6.2. Trong Quân Sự

• Pháo binh: Tính toán quỹ đạo đạn pháo để bắn trúng mục tiêu.
• Ném bom: Xác định thời điểm và vị trí thả bom để đạt hiệu quả cao nhất.

6.3. Trong Đời Sống Hàng Ngày

• Tưới cây: Điều chỉnh vòi nước để nước phun đến đúng vị trí cần tưới.
• Xây dựng: Tính toán độ dốc của mái nhà để nước mưa thoát dễ dàng.
• Thiết kế trò chơi: Mô phỏng chuyển động của các vật thể trong trò chơi điện tử.

7. Bài Tập Vận Dụng Về Chuyển Động Ném Ngang

Câu 1: Một vật được ném ngang từ độ cao 45m so với mặt đất, vận tốc ban đầu là 20 m/s. Bỏ qua sức cản của không khí, lấy g = 10 m/s². Tính tầm xa của vật.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 45}{10}} = 3s$
• Tầm xa: $L = v_0t = 20 cdot 3 = 60m$

Câu 2: Một máy bay đang bay ngang ở độ cao 500m với vận tốc 360 km/h, thả một kiện hàng xuống đất. Lấy g = 10 m/s². Tính khoảng cách từ vị trí thả hàng đến điểm chạm đất của kiện hàng.

Hướng dẫn:

• Đổi vận tốc: $v_0 = 360 km/h = 100 m/s$
• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 500}{10}} = 10s$
• Khoảng cách: $L = v_0t = 100 cdot 10 = 1000m$

Câu 3: Một quả bóng được ném ngang từ sân thượng của một tòa nhà cao 20m với vận tốc ban đầu 5 m/s. Xác định vận tốc của quả bóng khi chạm đất.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 20}{10}} = 2s$
• Vận tốc theo phương ngang: $v_x = v_0 = 5 m/s$
• Vận tốc theo phương thẳng đứng: $v_y = gt = 10 cdot 2 = 20 m/s$
• Vận tốc khi chạm đất: $v = sqrt{v_x^2 + v_y^2} = sqrt{5^2 + 20^2} = sqrt{425} approx 20.62 m/s$

Câu 4: Từ độ cao h = 10m, một vật được ném ngang với vận tốc ban đầu $v_0$. Biết rằng khi chạm đất, vận tốc của vật là 15m/s. Tính $v_0$.

Hướng dẫn:

• Vận tốc theo phương thẳng đứng khi chạm đất: $v_y = sqrt{2gh} = sqrt{2 cdot 10 cdot 10} = 10sqrt{2} m/s$
• Áp dụng định lý Pythagoras: $v^2 = v_0^2 + v_y^2 Rightarrow v_0 = sqrt{v^2 – v_y^2} = sqrt{15^2 – (10sqrt{2})^2} = sqrt{225 – 200} = sqrt{25} = 5 m/s$

Câu 5: Một vật được ném ngang từ độ cao 5m với vận tốc ban đầu 8m/s. Tính góc hợp bởi vectơ vận tốc của vật và phương ngang khi vật chạm đất.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 5}{10}} = 1s$
• Vận tốc theo phương thẳng đứng khi chạm đất: $v_y = gt = 10 cdot 1 = 10 m/s$
• Góc hợp bởi vectơ vận tốc và phương ngang: $tantheta = frac{v_y}{v_x} = frac{10}{8} = 1.25 Rightarrow theta = arctan(1.25) approx 51.34^circ$

Câu 6: Một hòn đá được ném theo phương ngang từ một vách đá cao 30m so với mặt nước biển. Vận tốc ban đầu của hòn đá là 15 m/s. Tính khoảng cách từ chân vách đá đến điểm mà hòn đá chạm mặt nước biển.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 30}{10}} = sqrt{6} s$
• Khoảng cách: $L = v_0t = 15 cdot sqrt{6} approx 36.74 m$

Câu 7: Một vận động viên nhảy xa chạy đà và nhảy lên với vận tốc theo phương ngang là 9 m/s. Giả sử độ cao từ lúc vận động viên rời mặt đất đến khi chạm đất là 1m. Tính tầm xa của cú nhảy.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 1}{10}} = sqrt{0.2} approx 0.45 s$
• Tầm xa: $L = v_0t = 9 cdot sqrt{0.2} approx 4.02 m$

Câu 8: Từ một máy bay đang bay ở độ cao 1200m với vận tốc 180 km/h, người ta thả một gói hàng. Tính thời gian để gói hàng chạm đất và khoảng cách từ điểm thả hàng đến điểm chạm đất (theo phương ngang). Bỏ qua sức cản của không khí và lấy g = 9.8 m/s².

Hướng dẫn:

• Đổi vận tốc: $v_0 = 180 km/h = 50 m/s$
• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 1200}{9.8}} approx 15.65 s$
• Khoảng cách: $L = v_0t = 50 cdot 15.65 approx 782.5 m$

Câu 9: Một khẩu pháo đặt trên một đỉnh đồi cao 50m so với đồng bằng bắn một viên đạn theo phương ngang với vận tốc ban đầu 200 m/s. Tính khoảng cách từ chân đồi đến điểm mà viên đạn chạm đất.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 50}{10}} = sqrt{10} approx 3.16 s$
• Khoảng cách: $L = v_0t = 200 cdot sqrt{10} approx 632.46 m$

Câu 10: Một người ném một quả bóng từ độ cao 1.5m so với mặt đất theo phương ngang với vận tốc 25 m/s. Tính tầm xa của quả bóng.

Hướng dẫn:

• Thời gian rơi: $t = sqrt{frac{2h}{g}} = sqrt{frac{2 cdot 1.5}{9.8}} approx 0.55 s$
• Tầm xa: $L = v_0t = 25 cdot 0.55 approx 13.75 m$

8. Câu Hỏi Thường Gặp (FAQ)

1. Gia tốc trong chuyển động ném ngang có đổi hướng không?

Không, gia tốc trong chuyển động ném ngang luôn hướng theo phương thẳng đứng xuống dưới do tác dụng của trọng lực.

2. Quỹ đạo của chuyển động ném ngang có dạng gì?

Quỹ đạo của chuyển động ném ngang có dạng một đường parabol.

3. Yếu tố nào quyết định tầm xa của vật trong chuyển động ném ngang?

Tầm xa của vật phụ thuộc vào vận tốc ban đầu và độ cao ban đầu.

4. Làm thế nào để tính thời gian chuyển động của vật trong chuyển động ném ngang?

Thời gian chuyển động của vật được tính bằng công thức $t = sqrt{frac{2h}{g}}$, trong đó h là độ cao ban đầu và g là gia tốc trọng trường.

5. Vận tốc của vật khi chạm đất trong chuyển động ném ngang phụ thuộc vào yếu tố nào?

Vận tốc khi chạm đất phụ thuộc vào vận tốc ban đầu và độ cao ban đầu.

6. Tại sao chúng ta thường bỏ qua sức cản của không khí trong các bài toán về chuyển động ném ngang?

Để đơn giản hóa bài toán và tập trung vào các yếu tố chính ảnh hưởng đến chuyển động. Trong thực tế, sức cản của không khí có thể ảnh hưởng đáng kể đến kết quả.

7. Chuyển động ném ngang có ứng dụng gì trong thể thao?

Chuyển động ném ngang được ứng dụng trong nhiều môn thể thao như bóng rổ, bóng chuyền, nhảy xa, ném lao,…

8. Làm thế nào để tối ưu hóa tầm xa trong chuyển động ném ngang?

Để tối ưu hóa tầm xa, cần điều chỉnh vận tốc ban đầu và góc ném (nếu có) sao cho phù hợp với độ cao ban đầu và điều kiện môi trường.

9. Sự khác biệt giữa chuyển động ném ngang và chuyển động ném xiên là gì?

Chuyển động ném ngang có vận tốc ban đầu theo phương ngang, trong khi chuyển động ném xiên có vận tốc ban đầu tạo một góc với phương ngang.

10. Làm thế nào để học tốt về chuyển động ném ngang?

Bạn nên nắm vững lý thuyết, làm nhiều bài tập vận dụng, và tham khảo các nguồn tài liệu uy tín như tic.edu.vn.

9. Khám Phá Thêm Tại Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng một cách hiệu quả? Hãy đến với tic.edu.vn, nơi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ càng.

• Nguồn tài liệu phong phú: Từ sách giáo khoa, bài tập, đến các tài liệu tham khảo chuyên sâu, tic.edu.vn đáp ứng mọi nhu cầu học tập của bạn.
• Thông tin giáo dục cập nhật: Luôn cập nhật những thông tin mới nhất về giáo dục, phương pháp học tập tiên tiến, và các xu hướng phát triển kỹ năng.
• Công cụ hỗ trợ học tập: Các công cụ trực tuyến giúp bạn ghi chú, quản lý thời gian, và học tập hiệu quả hơn.
• Cộng đồng học tập sôi nổi: Tham gia cộng đồng để trao đổi kiến thức, kinh nghiệm, và học hỏi lẫn nhau.

Đừng bỏ lỡ cơ hội khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả tại tic.edu.vn. Truy cập ngay hôm nay để bắt đầu hành trình chinh phục tri thức!

Liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn