**Tổng Hợp Kiến Thức Toán 12** Đầy Đủ Nhất Cho Kỳ Thi THPT

Tổng Hợp Kiến Thức Toán 12 là chìa khóa giúp bạn chinh phục kỳ thi THPT Quốc gia và các bài kiểm tra trên lớp. tic.edu.vn mang đến nguồn tài liệu tổng hợp kiến thức Toán 12 đầy đủ, chi tiết, giúp bạn hệ thống hóa kiến thức, ôn luyện hiệu quả và đạt điểm cao.

1. Tại Sao Cần Tổng Hợp Kiến Thức Toán 12?

Việc tổng hợp kiến thức Toán 12 mang lại nhiều lợi ích thiết thực cho học sinh, đặc biệt trong giai đoạn ôn thi quan trọng:

• Hệ thống hóa kiến thức: Giúp học sinh nhìn nhận tổng quan chương trình Toán 12, liên kết các kiến thức rời rạc thành một hệ thống logic.
• Nắm vững kiến thức trọng tâm: Xác định và tập trung vào các kiến thức quan trọng, thường xuyên xuất hiện trong các đề thi.
• Ôn luyện hiệu quả: Dễ dàng tra cứu, ôn tập và vận dụng kiến thức vào giải bài tập.
• Tiết kiệm thời gian: Thay vì tìm kiếm thông tin từ nhiều nguồn khác nhau, học sinh có thể tìm thấy tất cả kiến thức cần thiết ở một nơi.
• Tự tin khi làm bài: Nắm vững kiến thức giúp học sinh tự tin hơn khi đối mặt với các bài kiểm tra và kỳ thi.

Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc tổng hợp kiến thức giúp học sinh tăng khả năng ghi nhớ và vận dụng kiến thức lên đến 30%.

2. Tổng Quan Chương Trình Toán 12

Chương trình Toán 12 bao gồm hai phần chính: Giải tích và Hình học.

2.1. Giải Tích 12

• Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số:
  • Sự biến thiên của hàm số
  • Cực trị của hàm số
  • Đường tiệm cận
  • Khảo sát và vẽ đồ thị hàm số
• Hàm số lũy thừa, hàm số mũ và hàm số logarit:
  • Lũy thừa
  • Hàm số lũy thừa
  • Logarit
  • Hàm số mũ và hàm số logarit
  • Phương trình mũ và phương trình logarit
  • Bất phương trình mũ và bất phương trình logarit
• Nguyên hàm – Tích phân và ứng dụng:
  • Nguyên hàm
  • Tích phân
  • Ứng dụng của tích phân
• Số phức:
  • Số phức
  • Các phép toán trên tập số phức
  • Phương trình bậc hai với hệ số thực

2.2. Hình Học 12

• Khối đa diện:
  • Định nghĩa khối đa diện
  • Phân loại khối đa diện
  • Thể tích khối đa diện
• Mặt nón – Mặt trụ – Mặt cầu:
  • Mặt nón
  • Mặt trụ
  • Mặt cầu
• Tọa độ trong không gian:
  • Hệ tọa độ Oxyz
  • Phương trình mặt phẳng
  • Phương trình đường thẳng
  • Vị trí tương đối giữa các đối tượng

3. Tổng Hợp Chi Tiết Kiến Thức Toán 12 (Đại Số)

3.1. Công Thức Lũy Thừa

• Định nghĩa: $a^n = a.a.a…a$ (n thừa số a), với n là số nguyên dương.
• Tính chất:
  • $a^m . a^n = a^{m+n}$
  • $frac{a^m}{a^n} = a^{m-n}$
  • $(a^m)^n = a^{m.n}$
  • $(a.b)^n = a^n . b^n$
  • $(frac{a}{b})^n = frac{a^n}{b^n}$
• Lũy thừa với số mũ hữu tỉ: $a^{frac{m}{n}} = sqrt[n]{a^m}$ (a > 0)
• Lũy thừa với số mũ thực: $a^{alpha}$ (a > 0, $alpha$ là số thực)

3.2. Công Thức Logarit

• Định nghĩa: $log_a b = x Leftrightarrow a^x = b$ (a > 0, a ≠ 1, b > 0)
• Tính chất:
  • $log_a 1 = 0$
  • $log_a a = 1$
  • $log_a (b.c) = log_a b + log_a c$
  • $log_a (frac{b}{c}) = log_a b – log_a c$
  • $log_a b^n = n.log_a b$
  • $log_a b = frac{log_c b}{log_c a}$
  • $log_a b = frac{1}{log_b a}$
• Logarit thập phân: $log b = log_{10} b$
• Logarit tự nhiên (logarit Nepe): $ln b = log_e b$ (e ≈ 2.71828)

3.3. Công Thức Hàm Số Lũy Thừa – Mũ – Logarit

• Hàm số lũy thừa: $y = x^{alpha}$ ($alpha$ là số thực)
• Hàm số mũ: $y = a^x$ (a > 0, a ≠ 1)
• Hàm số logarit: $y = log_a x$ (a > 0, a ≠ 1)

Hàm số	Tập xác định	Đạo hàm
$y = x^alpha$	$R$	$y’ = alpha x^{alpha-1}$
$y = a^x$	$R$	$y’ = a^x ln a$
$y = log_a x$	$(0; +infty)$	$y’ = frac{1}{x ln a}$

3.4. Công Thức Phương Trình Mũ và Logarit

• Phương trình mũ cơ bản: $a^x = b$
  • Nếu b > 0: $x = log_a b$
  • Nếu b ≤ 0: phương trình vô nghiệm
• Phương trình logarit cơ bản: $log_a x = b$
  • $x = a^b$

3.5. Công Thức Bất Phương Trình Mũ và Logarit

• Bất phương trình mũ:
  • $a^x > b$:
    • Nếu a > 1: $x > log_a b$
    • Nếu 0 < a < 1: $x < log_a b$
• Bất phương trình logarit:
  • $log_a x > b$:
    • Nếu a > 1: $x > a^b$
    • Nếu 0 < a < 1: $0 < x < a^b$

3.6. Công Thức Đạo Hàm

• $(u + v)’ = u’ + v’$
• $(u – v)’ = u’ – v’$
• $(u.v)’ = u’.v + u.v’$
• $(frac{u}{v})’ = frac{u’.v – u.v’}{v^2}$
• $(f(u))’ = f'(u).u’$
• $(sinx)’ = cosx$
• $(cosx)’ = -sinx$
• $(tanx)’ = frac{1}{cos^2x} = 1 + tan^2x$
• $(cotx)’ = -frac{1}{sin^2x} = -(1 + cot^2x)$

3.7. Công Thức Nguyên Hàm

• $int x^n dx = frac{x^{n+1}}{n+1} + C$ (n ≠ -1)
• $int frac{1}{x} dx = ln|x| + C$
• $int e^x dx = e^x + C$
• $int a^x dx = frac{a^x}{ln a} + C$
• $int sinx dx = -cosx + C$
• $int cosx dx = sinx + C$
• $int frac{1}{cos^2x} dx = tanx + C$
• $int frac{1}{sin^2x} dx = -cotx + C$

3.8. Công Thức Diện Tích và Thể Tích

• Diện tích:
  • Hình chữ nhật: S = a.b
  • Hình vuông: S = a^2
  • Tam giác: S = 1/2.a.h
  • Hình tròn: S = πr^2
• Thể tích:
  • Hình hộp chữ nhật: V = a.b.c
  • Hình lập phương: V = a^3
  • Hình chóp: V = 1/3.S.h
  • Hình trụ: V = πr^2h
  • Hình nón: V = 1/3.πr^2h
  • Hình cầu: V = 4/3.πr^3

3.9. Công Thức Chuyển Động

• Vận tốc trung bình: $v_{tb} = frac{s}{t}$ (s là quãng đường, t là thời gian)
• Gia tốc: $a = frac{Delta v}{Delta t}$
• Chuyển động thẳng đều: $s = v_0t + frac{1}{2}at^2$
• Vận tốc trong chuyển động thẳng biến đổi đều: $v = v_0 + at$

3.10. Công Thức Lượng Giác

• Hệ thức cơ bản:
  • $sin^2x + cos^2x = 1$
  • $tanx = frac{sinx}{cosx}$
  • $cotx = frac{cosx}{sinx}$
  • $tanx.cotx = 1$
  • $1 + tan^2x = frac{1}{cos^2x}$
  • $1 + cot^2x = frac{1}{sin^2x}$
• Cung liên kết:
  • $sin(π – x) = sinx$
  • $cos(π – x) = -cosx$
  • $tan(π – x) = -tanx$
  • $cot(π – x) = -cotx$
• Công thức cộng:
  • $sin(a + b) = sina.cosb + cosa.sinb$
  • $sin(a – b) = sina.cosb – cosa.sinb$
  • $cos(a + b) = cosa.cosb – sina.sinb$
  • $cos(a – b) = cosa.cosb + sina.sinb$
  • $tan(a + b) = frac{tana + tanb}{1 – tana.tanb}$
  • $tan(a – b) = frac{tana – tanb}{1 + tana.tanb}$
• Công thức nhân đôi:
  • $sin2x = 2sinx.cosx$
  • $cos2x = cos^2x – sin^2x = 2cos^2x – 1 = 1 – 2sin^2x$
  • $tan2x = frac{2tanx}{1 – tan^2x}$

3.11. Công Thức Phương Trình Lượng Giác

• $sinx = sina Leftrightarrow begin{cases} x = a + k2π x = π – a + k2π end{cases}$
• $cosx = cosa Leftrightarrow x = ±a + k2π$
• $tanx = tana Leftrightarrow x = a + kπ$
• $cotx = cota Leftrightarrow x = a + kπ$ (k ∈ Z)

3.12. Công Thức Tổ Hợp – Xác Suất

• Quy tắc cộng: Nếu có n cách chọn một phần tử từ tập A và m cách chọn một phần tử từ tập B (A và B không giao nhau), thì có n + m cách chọn một phần tử từ A hoặc B.
• Quy tắc nhân: Nếu có n cách thực hiện hành động A và m cách thực hiện hành động B, thì có n.m cách thực hiện cả hai hành động A và B.
• Hoán vị: $P_n = n! = 1.2.3…n$
• Chỉnh hợp: $A_n^k = frac{n!}{(n-k)!}$ (0 ≤ k ≤ n)
• Tổ hợp: $C_n^k = frac{n!}{k!(n-k)!}$ (0 ≤ k ≤ n)
• Xác suất: $P(A) = frac{n(A)}{n(Omega)}$ (n(A) là số kết quả thuận lợi cho A, n(Ω) là tổng số kết quả có thể xảy ra)

3.13. Công Thức Khai Triển Nhị Thức Newton

• $(a + b)^n = sum_{k=0}^{n} C_n^k a^{n-k} b^k = C_n^0 a^n + C_n^1 a^{n-1} b + … + C_n^n b^n$
• Số hạng tổng quát: $T_{k+1} = C_n^k a^{n-k} b^k$

3.14. Công Thức Cấp Số Cộng – Cấp Số Nhân

• Cấp số cộng:
  • $u_{n+1} = u_n + d$ (d là công sai)
  • $u_n = u_1 + (n – 1)d$
  • $S_n = frac{n(u_1 + u_n)}{2} = frac{n[2u_1 + (n-1)d]}{2}$
• Cấp số nhân:
  • $u_{n+1} = u_n . q$ (q là công bội)
  • $u_n = u_1 . q^{n-1}$
  • $S_n = u_1 . frac{1 – q^n}{1 – q}$ (q ≠ 1)

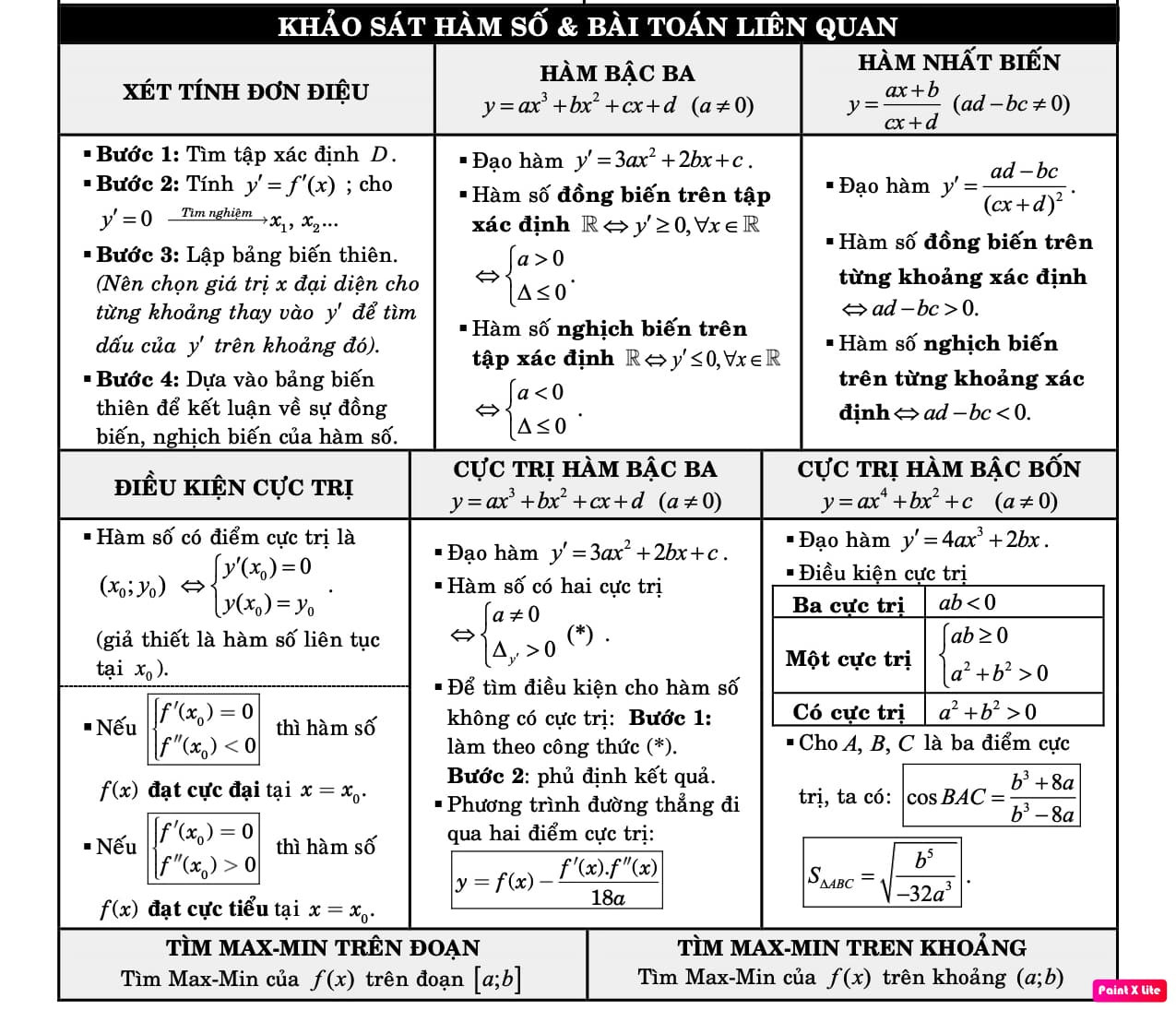
3.15. Khảo Sát Hàm Số và Các Dạng Toán Liên Quan

• Các bước khảo sát hàm số:
  1. Tìm tập xác định
  2. Tính đạo hàm y’, tìm các điểm mà y’ = 0 hoặc y’ không xác định
  3. Lập bảng biến thiên
  4. Tìm cực trị
  5. Tìm giới hạn tại vô cực và tiệm cận (nếu có)
  6. Vẽ đồ thị hàm số
• Hàm số bậc 3: $y = ax^3 + bx^2 + cx + d$
• Hàm số nhất biến: $y = frac{ax + b}{cx + d}$

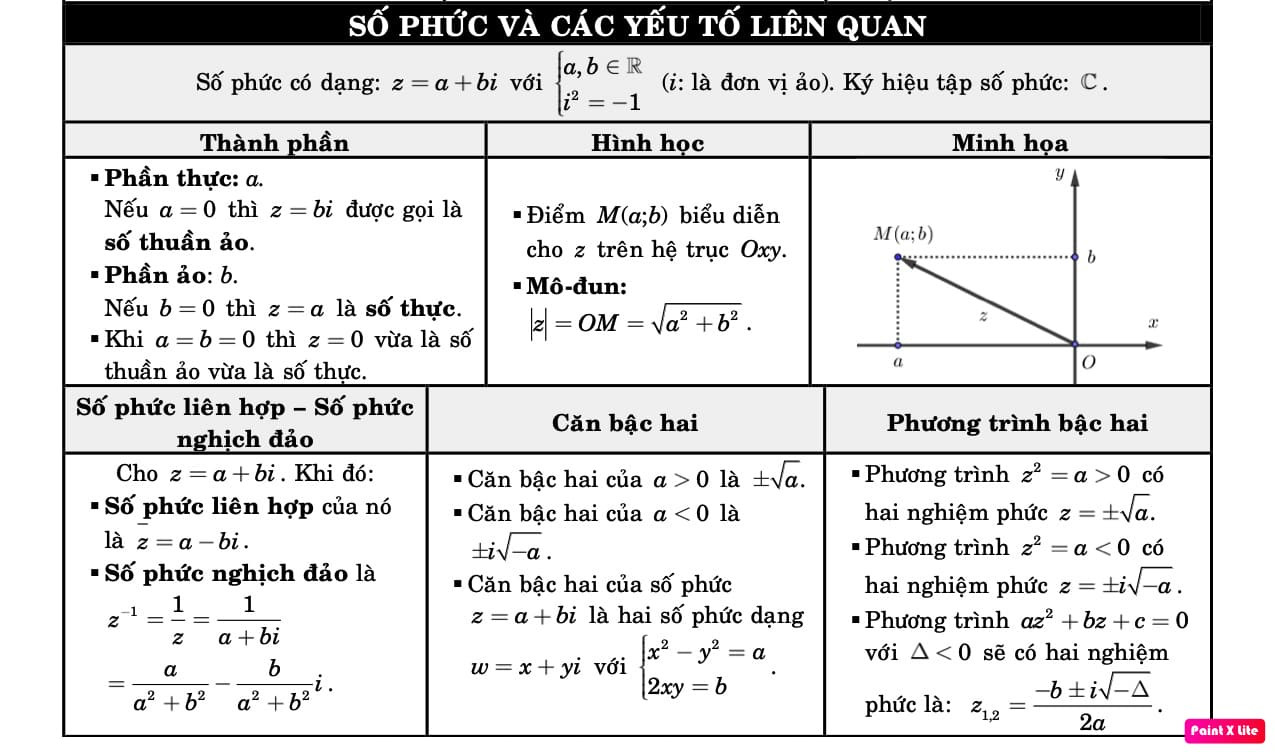
3.16. Số Phức và Các Yếu Tố Liên Quan

• Định nghĩa: $z = a + bi$ (a, b ∈ R, i là đơn vị ảo, $i^2 = -1$)
• Số phức liên hợp: $bar{z} = a – bi$
• Module của số phức: $|z| = sqrt{a^2 + b^2}$
• Các phép toán:
  • Cộng: $(a + bi) + (c + di) = (a + c) + (b + d)i$
  • Trừ: $(a + bi) – (c + di) = (a – c) + (b – d)i$
  • Nhân: $(a + bi)(c + di) = (ac – bd) + (ad + bc)i$
  • Chia: $frac{a + bi}{c + di} = frac{(a + bi)(c – di)}{(c + di)(c – di)} = frac{(ac + bd) + (bc – ad)i}{c^2 + d^2}$

4. Tổng Hợp Chi Tiết Kiến Thức Toán 12 (Hình Học)

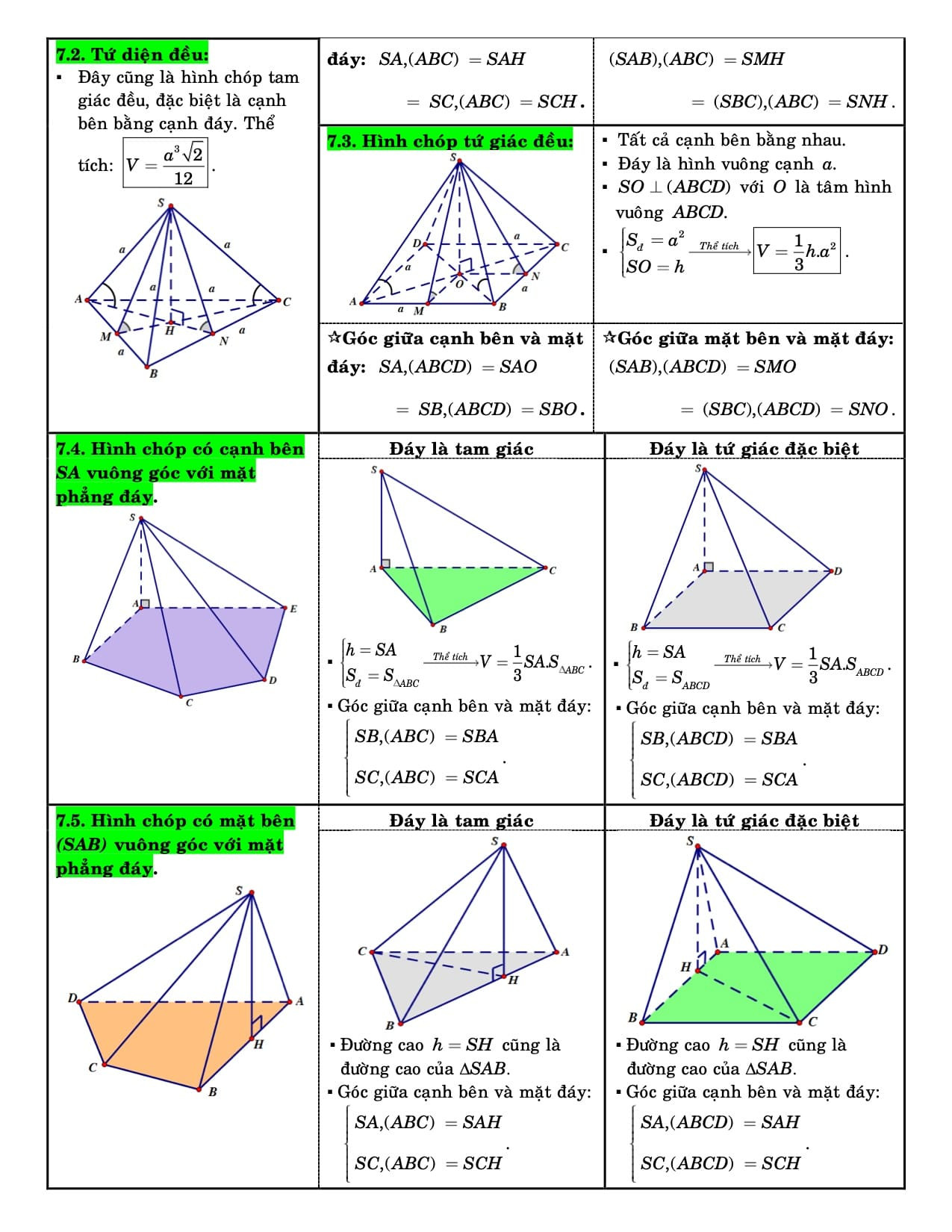
4.1. Khối Đa Diện và Thể Tích Của Chúng

• Khối đa diện: Hình được bao bởi các đa giác phẳng.
• Phân loại:
  • Khối đa diện lồi
  • Khối đa diện đều
• Các loại khối đa diện thường gặp:
  • Hình chóp
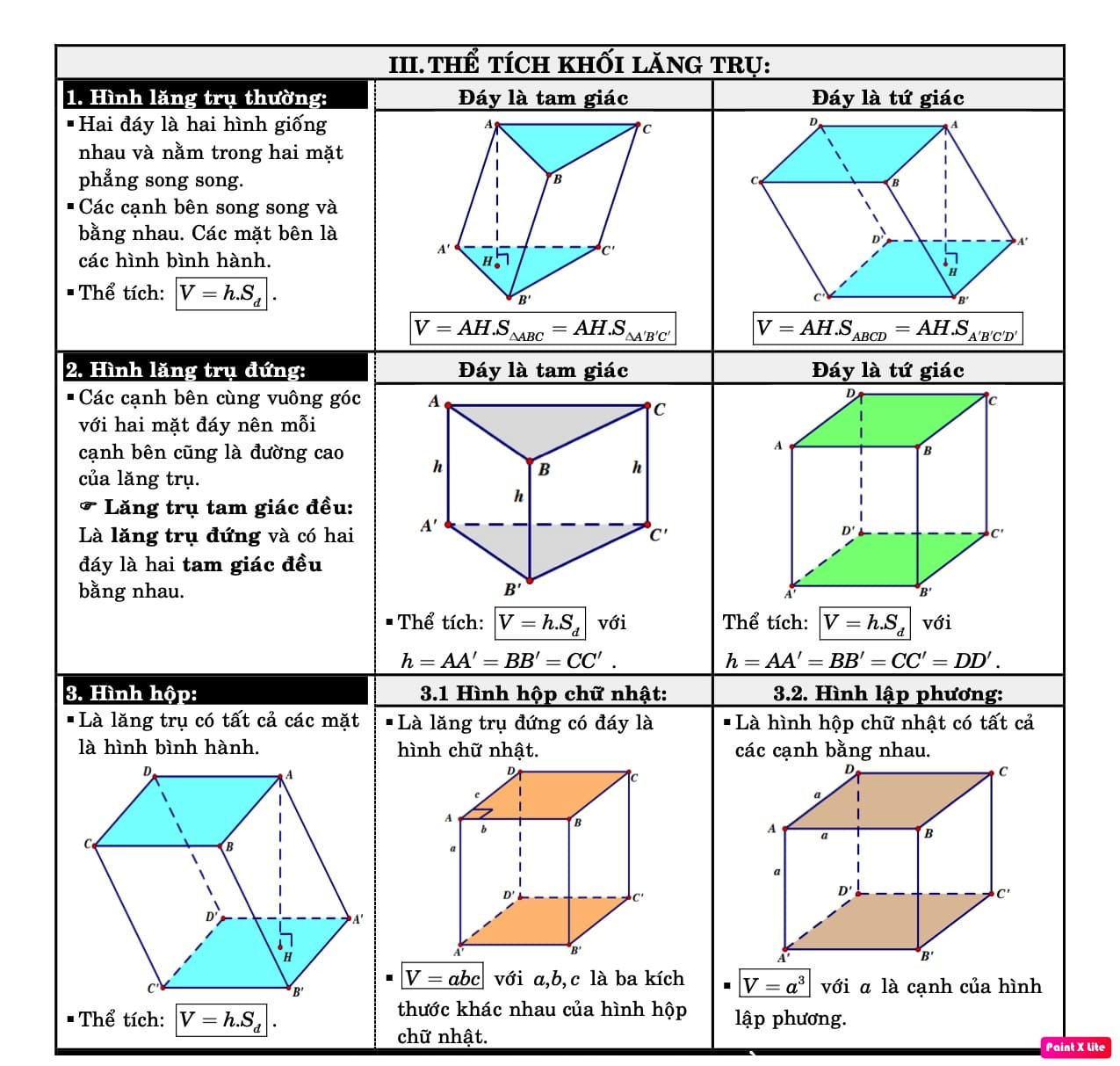
  • Hình lăng trụ
• Công thức tính thể tích:
  • Hình chóp: $V = frac{1}{3}S_{đáy}.h$
  • Hình lăng trụ: $V = S_{đáy}.h$

4.2. Mặt Trụ – Mặt Nón – Mặt Cầu

• Mặt trụ: Hình được tạo thành khi quay một hình chữ nhật quanh một cạnh.
  • Diện tích xung quanh: $S_{xq} = 2πrh$
  • Thể tích: $V = πr^2h$
• Mặt nón: Hình được tạo thành khi quay một tam giác vuông quanh một cạnh góc vuông.
  • Diện tích xung quanh: $S_{xq} = πrl$ (l là đường sinh)
  • Thể tích: $V = frac{1}{3}πr^2h$
• Mặt cầu: Tập hợp các điểm cách đều một điểm cố định (tâm) một khoảng không đổi (bán kính).
  • Diện tích: $S = 4πr^2$
  • Thể tích: $V = frac{4}{3}πr^3$

4.3. Hình Học Giải Tích Trong Không Gian

• Hệ tọa độ Oxyz: Gồm ba trục Ox, Oy, Oz vuông góc với nhau tại gốc O.
• Tọa độ vectơ: $vec{a} = (x; y; z)$
• Tọa độ điểm: $A(x; y; z)$
• Phương trình mặt cầu: $(x – a)^2 + (y – b)^2 + (z – c)^2 = R^2$ (tâm I(a; b; c), bán kính R)
• Phương trình mặt phẳng: $Ax + By + Cz + D = 0$
• Phương trình đường thẳng:
  • Dạng tham số: $begin{cases} x = x_0 + at y = y_0 + bt z = z_0 + ct end{cases}$ (đi qua $M_0(x_0; y_0; z_0)$, vectơ chỉ phương $vec{u} = (a; b; c)$)
  • Dạng chính tắc: $frac{x – x_0}{a} = frac{y – y_0}{b} = frac{z – z_0}{c}$

5. Mẹo Học Toán 12 Hiệu Quả

• Nắm vững lý thuyết: Học kỹ các định nghĩa, định lý, công thức.
• Làm bài tập đa dạng: Luyện tập từ cơ bản đến nâng cao, từ sách giáo khoa đến đề thi thử.
• Sử dụng sơ đồ tư duy: Hệ thống hóa kiến thức bằng sơ đồ tư duy giúp dễ nhớ và dễ hiểu.
• Học nhóm: Trao đổi kiến thức, giải đáp thắc mắc cùng bạn bè.
• Tìm kiếm sự giúp đỡ: Đừng ngần ngại hỏi thầy cô, gia sư hoặc bạn bè khi gặp khó khăn.
• Sử dụng tài liệu tham khảo: Tham khảo các sách nâng cao, đề thi thử, tài liệu trên mạng.
• Giữ tinh thần thoải mái: Đừng tạo áp lực quá lớn cho bản thân, hãy học tập một cách vui vẻ và hiệu quả.

6. Tic.edu.vn – Người Bạn Đồng Hành Tin Cậy

tic.edu.vn tự hào là website cung cấp tài liệu học tập chất lượng cao, luôn sẵn sàng đồng hành cùng các bạn học sinh trên con đường chinh phục tri thức. Chúng tôi cung cấp:

• Nguồn tài liệu đa dạng: Tổng hợp đầy đủ kiến thức Toán 12, bao gồm lý thuyết, công thức, bài tập, đề thi.
• Thông tin cập nhật: Luôn cập nhật thông tin giáo dục mới nhất, chính xác nhất.
• Công cụ hỗ trợ học tập: Cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn học tập mọi lúc mọi nơi.
• Cộng đồng học tập sôi nổi: Tạo môi trường học tập trực tuyến, nơi bạn có thể giao lưu, học hỏi và chia sẻ kinh nghiệm với các bạn học sinh khác.

7. Ý Định Tìm Kiếm Của Người Dùng Về “Tổng Hợp Kiến Thức Toán 12”

1. Tìm kiếm công thức Toán 12 đầy đủ: Người dùng muốn tìm một tài liệu chứa tất cả các công thức quan trọng của chương trình Toán 12, bao gồm cả đại số và hình học.
2. Tìm kiếm tài liệu ôn thi THPT Quốc gia môn Toán: Người dùng cần tài liệu tổng hợp kiến thức Toán 12 để ôn thi THPT Quốc gia, bao gồm cả lý thuyết và bài tập.
3. Tìm kiếm phương pháp học Toán 12 hiệu quả: Người dùng muốn tìm các mẹo học tập, phương pháp giải bài tập nhanh và hiệu quả để cải thiện kết quả học tập môn Toán.
4. Tìm kiếm đề thi thử Toán 12 có đáp án: Người dùng muốn luyện tập với các đề thi thử Toán 12 để làm quen với cấu trúc đề thi và rèn luyện kỹ năng giải bài.
5. Tìm kiếm tài liệu tóm tắt kiến thức Toán 12: Người dùng cần một tài liệu ngắn gọn, dễ hiểu, tóm tắt những kiến thức trọng tâm của chương trình Toán 12 để ôn tập nhanh chóng.

8. Câu Hỏi Thường Gặp (FAQ)

1. Tôi có thể tìm thấy những loại tài liệu Toán 12 nào trên tic.edu.vn?

   tic.edu.vn cung cấp đa dạng tài liệu Toán 12, bao gồm: tóm tắt lý thuyết, công thức, bài tập có lời giải chi tiết, đề thi thử, video bài giảng và nhiều tài liệu tham khảo khác.

2. Làm thế nào để tìm kiếm tài liệu Toán 12 trên tic.edu.vn?

   Bạn có thể tìm kiếm tài liệu bằng cách sử dụng thanh tìm kiếm trên trang web, nhập từ khóa liên quan đến chủ đề bạn quan tâm (ví dụ: “tích phân”, “khối đa diện”, “số phức”). Bạn cũng có thể duyệt theo danh mục môn học và lớp học để tìm tài liệu phù hợp.

3. tic.edu.vn có cung cấp công cụ hỗ trợ học tập Toán 12 không?

   Có, tic.edu.vn cung cấp một số công cụ hỗ trợ học tập trực tuyến, như: máy tính bỏ túi, công cụ vẽ đồ thị hàm số, công cụ giải phương trình và hệ phương trình.

4. Tôi có thể tham gia cộng đồng học tập Toán 12 trên tic.edu.vn bằng cách nào?

   Bạn có thể tham gia cộng đồng học tập bằng cách đăng ký tài khoản trên tic.edu.vn, tham gia vào các diễn đàn thảo luận, đặt câu hỏi và chia sẻ kiến thức với các thành viên khác.

5. Làm thế nào để tôi có thể đóng góp tài liệu cho tic.edu.vn?

   Nếu bạn có tài liệu Toán 12 chất lượng muốn chia sẻ với cộng đồng, bạn có thể liên hệ với ban quản trị website qua email: [email protected].

6. tic.edu.vn có thường xuyên cập nhật tài liệu Toán 12 không?

   Chúng tôi luôn cố gắng cập nhật tài liệu thường xuyên để đảm bảo cung cấp cho bạn những thông tin mới nhất và chính xác nhất.

7. Tôi có thể sử dụng tài liệu trên tic.edu.vn miễn phí không?

   Đa số tài liệu trên tic.edu.vn đều được cung cấp miễn phí cho người dùng. Tuy nhiên, có thể có một số tài liệu nâng cao hoặc khóa học trực tuyến yêu cầu trả phí.

8. Tôi gặp khó khăn khi sử dụng website tic.edu.vn, tôi có thể liên hệ với ai để được hỗ trợ?

   Bạn có thể liên hệ với đội ngũ hỗ trợ của tic.edu.vn qua email: [email protected] hoặc qua số điện thoại được cung cấp trên trang web.

9. tic.edu.vn có những ưu điểm gì so với các website học tập khác?

   tic.edu.vn nổi bật với nguồn tài liệu đa dạng, được kiểm duyệt kỹ lưỡng, giao diện thân thiện, dễ sử dụng và cộng đồng học tập sôi nổi.

10. tic.edu.vn có những lời khuyên nào cho học sinh đang ôn thi Toán 12?

    tic.edu.vn khuyên bạn nên nắm vững kiến thức cơ bản, luyện tập thường xuyên, sử dụng tài liệu tham khảo hiệu quả, giữ tinh thần thoải mái và tìm kiếm sự giúp đỡ khi cần thiết.

9. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập Toán 12 chất lượng? Bạn muốn tiết kiệm thời gian và nâng cao hiệu quả ôn luyện? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. tic.edu.vn – Người bạn đồng hành tin cậy trên con đường chinh phục tri thức.

Thông tin liên hệ:

• Email: [email protected]
• Website: tic.edu.vn