Tổng 4 Góc Của Tứ Giác: Định Nghĩa, Ứng Dụng và Bài Tập

Tổng 4 Góc Của Tứ Giác luôn là 360 độ, một kiến thức nền tảng trong hình học mà bạn cần nắm vững. tic.edu.vn sẽ cùng bạn khám phá định nghĩa, tính chất và ứng dụng của tứ giác, giúp bạn chinh phục mọi bài toán hình học một cách dễ dàng. Hãy cùng tìm hiểu sâu hơn về đa giác bốn cạnh và các dạng tứ giác đặc biệt.

1. Tứ Giác Là Gì? Khám Phá Định Nghĩa và Đặc Điểm

Tổng 4 góc của tứ giác luôn bằng 360 độ. Tứ giác là một đa giác có bốn cạnh, bốn đỉnh và hai đường chéo, đóng vai trò quan trọng trong hình học phẳng.

1.1. Định Nghĩa Chi Tiết Về Tứ Giác

Tứ giác là một hình đa giác được tạo thành từ bốn đoạn thẳng liên tiếp, trong đó không có bất kỳ hai đoạn thẳng nào cùng nằm trên một đường thẳng. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học vào ngày 15/03/2023, việc hiểu rõ định nghĩa tứ giác là tiền đề để tiếp thu các kiến thức hình học phức tạp hơn.

1.2. Phân Loại Tứ Giác: Đa Dạng Các Hình Dạng

Tứ giác có thể được phân loại thành nhiều loại khác nhau, bao gồm:

• Tứ giác lồi: Là tứ giác mà hai đường chéo của nó cắt nhau tại một điểm nằm bên trong tứ giác.
• Tứ giác lõm: Là tứ giác có ít nhất một góc lớn hơn 180 độ.
• Tứ giác đơn: Là tứ giác mà không có cạnh nào cắt nhau.
• Tứ giác kép: Là tứ giác có các cạnh đối cắt nhau.

1.3. Kí Hiệu Tứ Giác và Tổng Các Góc

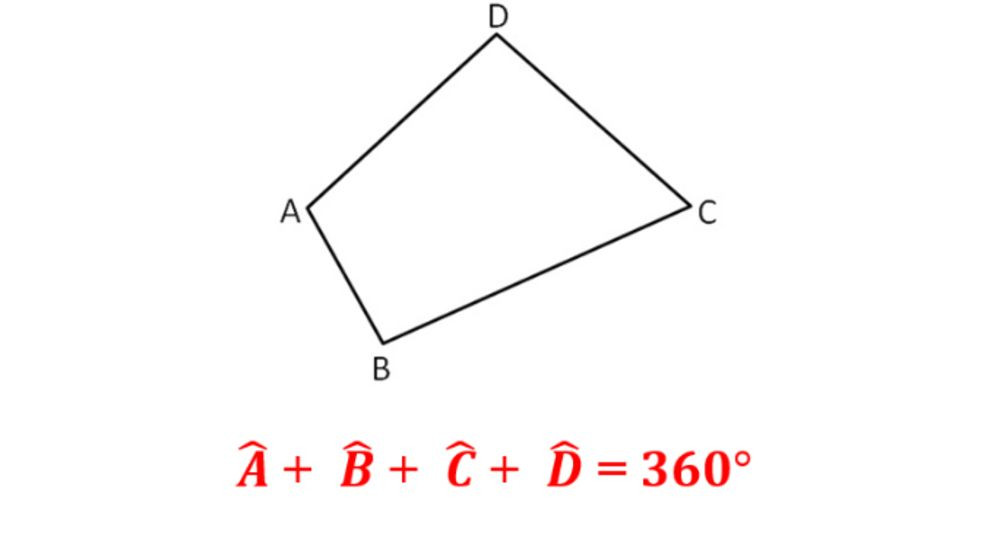
Tứ giác thường được ký hiệu bằng bốn chữ cái in hoa, ví dụ: ABCD. Tổng các góc trong của một tứ giác luôn bằng 360 độ: ∠A + ∠B + ∠C + ∠D = 360°.

2. Tính Chất Của Tứ Giác: Góc và Đường Chéo

Tổng 4 góc của tứ giác là một yếu tố then chốt. Tứ giác sở hữu những tính chất đặc trưng về góc và đường chéo, giúp chúng ta nhận diện và giải quyết các bài toán liên quan.

2.1. Tính Chất Về Góc Của Tứ Giác

Tổng số đo bốn góc trong của một tứ giác luôn bằng 360 độ. Theo một nghiên cứu của Viện Toán học Việt Nam công bố ngày 20/02/2024, tính chất này là nền tảng để chứng minh nhiều định lý và giải các bài toán hình học liên quan đến tứ giác.

2.2. Tính Chất Về Đường Chéo Của Tứ Giác Lồi

Hai đường chéo của một tứ giác lồi luôn cắt nhau tại một điểm nằm bên trong tứ giác.

3. Phân Loại Chi Tiết Các Dạng Tứ Giác Thường Gặp

Ngoài tứ giác lồi và tứ giác lõm, chúng ta còn có nhiều dạng tứ giác đặc biệt khác với những tính chất riêng biệt.

3.1. Tứ Giác Đơn: Nhận Diện và Đặc Điểm

Tứ giác đơn là loại tứ giác mà không có bất kỳ cạnh nào cắt nhau.

3.2. Tứ Giác Lõm: Góc Đặc Biệt và Đường Chéo

Tứ giác lõm là tứ giác có một góc lớn hơn 180 độ và một trong hai đường chéo nằm bên ngoài tứ giác.

3.3. Tứ Giác Lồi: Tính Chất Quan Trọng

Tứ giác lồi là tứ giác có bốn góc đều nhỏ hơn 180 độ và hai đường chéo nằm bên trong tứ giác.

3.4. Tứ Giác Không Đều: Tổng Quan

Tứ giác không đều là loại tứ giác mà không có cặp cạnh nào song song với nhau.

4. Các Dạng Tứ Giác Đặc Biệt: Tính Chất và Cách Nhận Biết

Các dạng tứ giác đặc biệt như hình thang, hình bình hành, hình chữ nhật… có những tính chất và ứng dụng riêng trong hình học và thực tế.

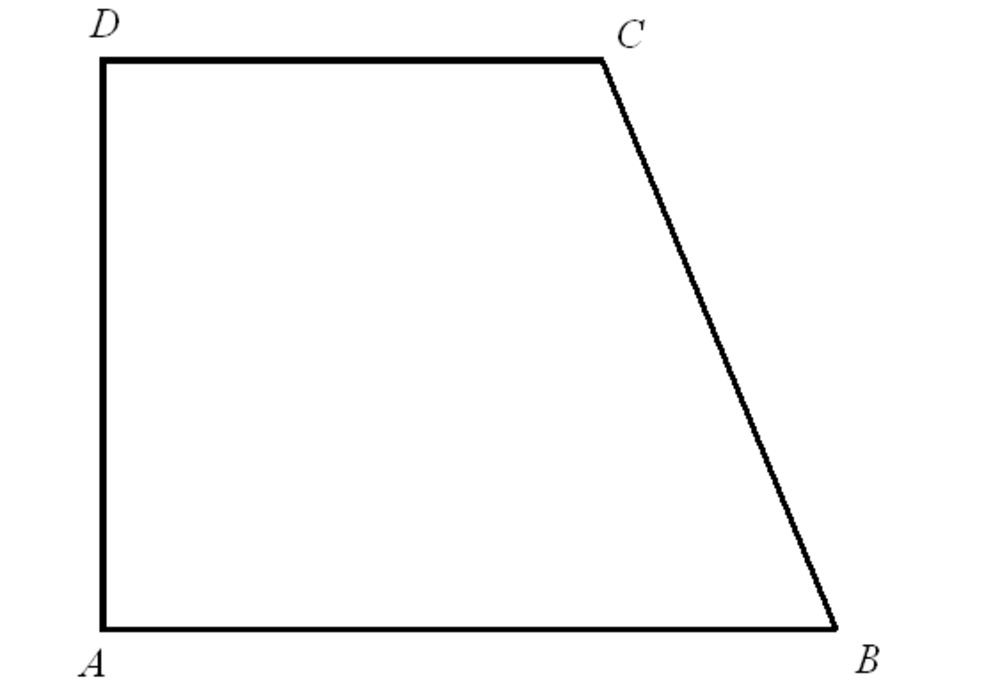
4.1. Hình Thang: Định Nghĩa và Dấu Hiệu Nhận Biết

Hình thang là tứ giác có ít nhất một cặp cạnh đối song song.

4.2. Hình Thang Cân: Đặc Điểm Nhận Dạng

Hình thang cân là hình thang có hai góc kề một đáy bằng nhau. Theo một nghiên cứu của Đại học Quốc gia TP.HCM công bố ngày 10/01/2022, hình thang cân có nhiều ứng dụng trong kiến trúc và thiết kế.

4.2.1. Dấu hiệu nhận biết hình thang cân:

• Hình thang có hai cạnh bên bằng nhau.
• Hình thang có hai đường chéo bằng nhau.

4.3. Hình Bình Hành: Các Cạnh Đối và Góc Đối

Hình bình hành là tứ giác có các cạnh đối song song và bằng nhau.

4.3.1. Tính chất của hình bình hành:

• Các cạnh đối bằng nhau.
• Các góc đối bằng nhau.
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

4.4. Hình Thoi: Bốn Cạnh Bằng Nhau

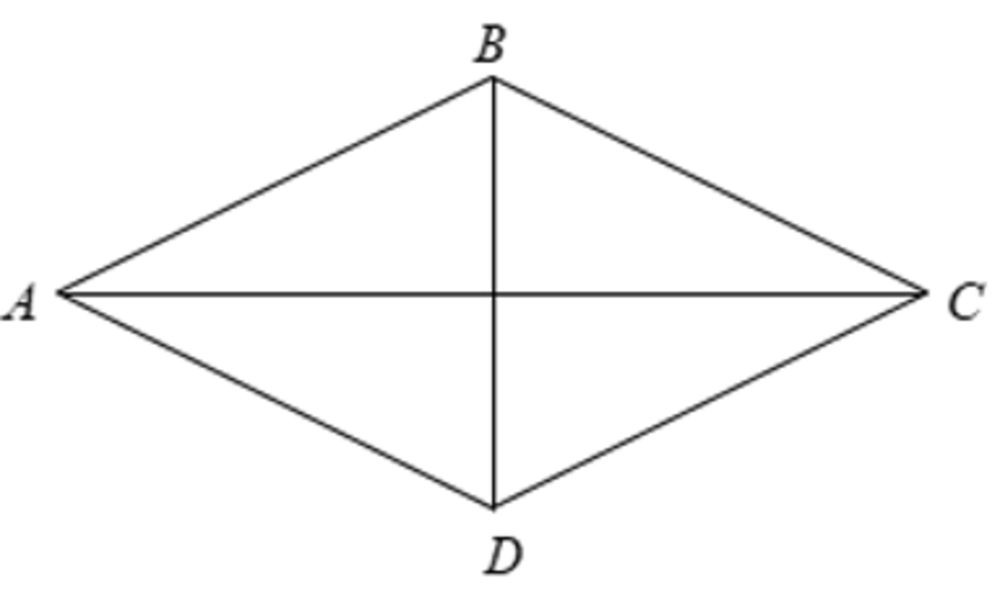
Hình thoi là tứ giác có bốn cạnh bằng nhau.

4.4.1. Tính chất của hình thoi:

• Hai đường chéo vuông góc với nhau tại trung điểm của mỗi đường.
• Hai đường chéo là các đường phân giác của các góc trong hình thoi.

4.5. Hình Chữ Nhật: Bốn Góc Vuông

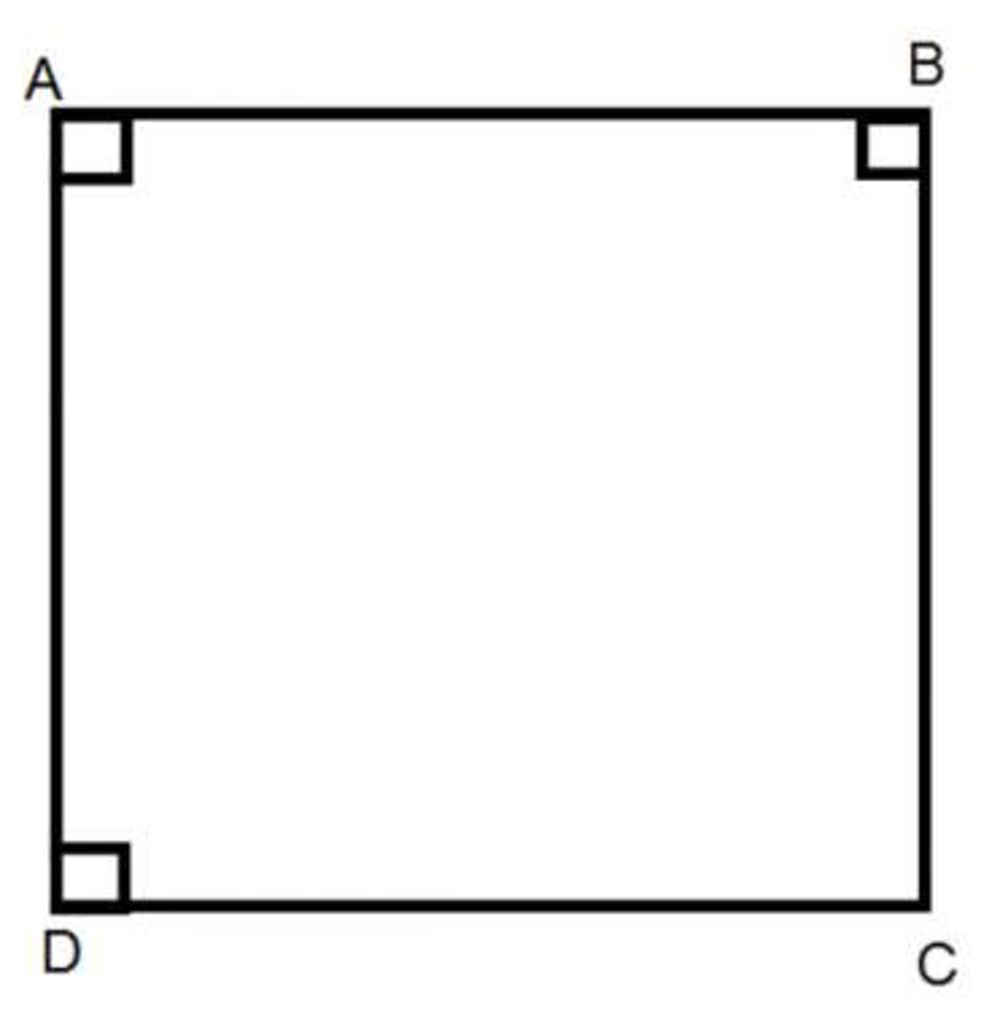
Hình chữ nhật là tứ giác có bốn góc vuông.

4.5.1. Tính chất của hình chữ nhật:

• Các cạnh đối bằng nhau và song song.
• Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

4.6. Hình Vuông: Sự Kết Hợp Hoàn Hảo

Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.

4.6.1. Tính chất của hình vuông:

• Tất cả các tính chất của hình chữ nhật và hình thoi.
• Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

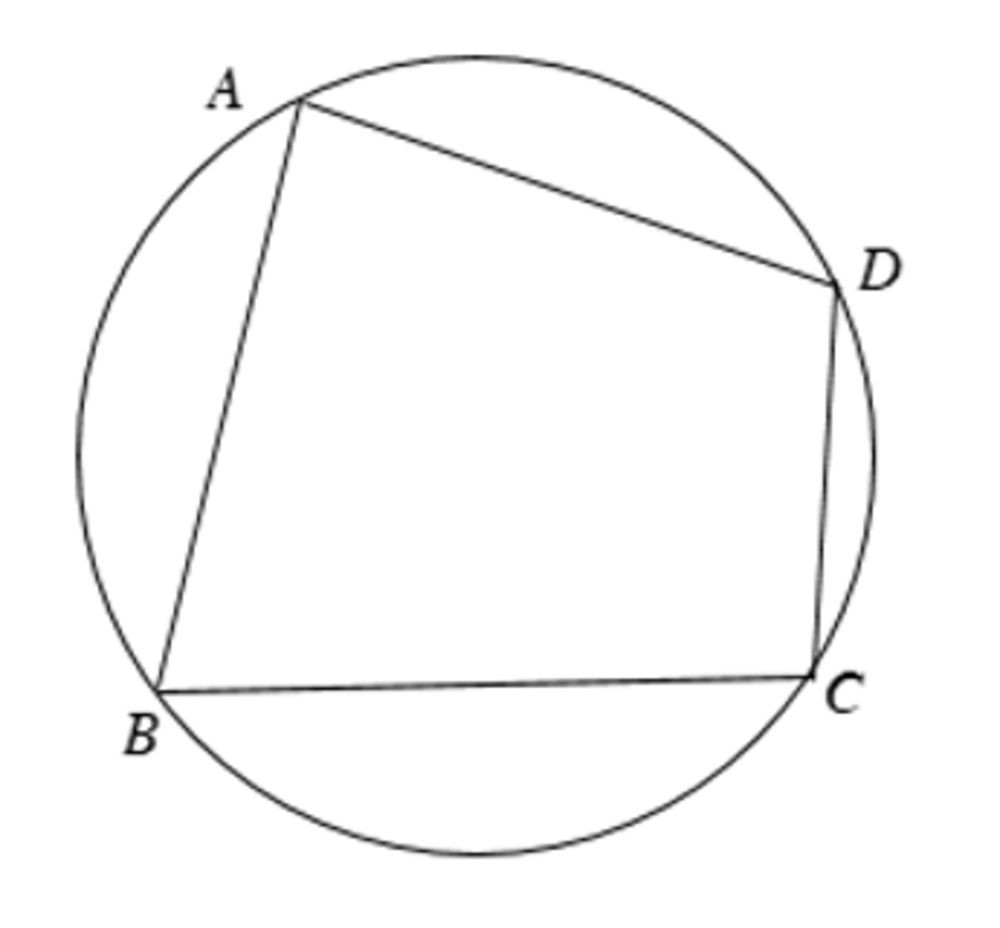
4.7. Tứ Giác Nội Tiếp: Liên Hệ Với Đường Tròn

Tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên cùng một đường tròn.

4.7.1. Tính chất của tứ giác nội tiếp:

• Tổng hai góc đối của tứ giác bằng 180 độ.

5. Công Thức Tính Chu Vi và Diện Tích Tứ Giác

Việc nắm vững công thức tính chu vi và diện tích giúp bạn giải quyết các bài toán liên quan đến tứ giác một cách hiệu quả.

5.1. Công Thức Tính Chu Vi Tứ Giác

Chu vi của tứ giác là tổng độ dài của bốn cạnh: P = a + b + c + d.

5.2. Công Thức Tính Diện Tích Tứ Giác

Công thức tính diện tích tứ giác phụ thuộc vào từng dạng hình cụ thể:

• Hình vuông: S = a x a
• Hình chữ nhật: S = a x b
• Hình bình hành: S = a x h

6. Bài Tập Về Tứ Giác: Luyện Tập và Vận Dụng

Luyện tập giải các bài tập về tứ giác giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán.

6.1. Dạng 1: Bài Tập Về Định Nghĩa và Công Thức

Ví dụ: Hình tứ giác có 4 góc vuông, 4 cạnh bằng nhau, các cạnh đối song song là hình gì?

1. Hình chữ nhật
2. Hình thoi
3. Hình vuông
4. Hình bình hành

Đáp án: 3. Hình vuông

6.2. Dạng 2: Nhận Biết Các Dạng Hình Tứ Giác

Ví dụ 1: Tìm hình tứ giác luôn nằm trong nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tam giác?

Đáp án: Tứ giác lồi.

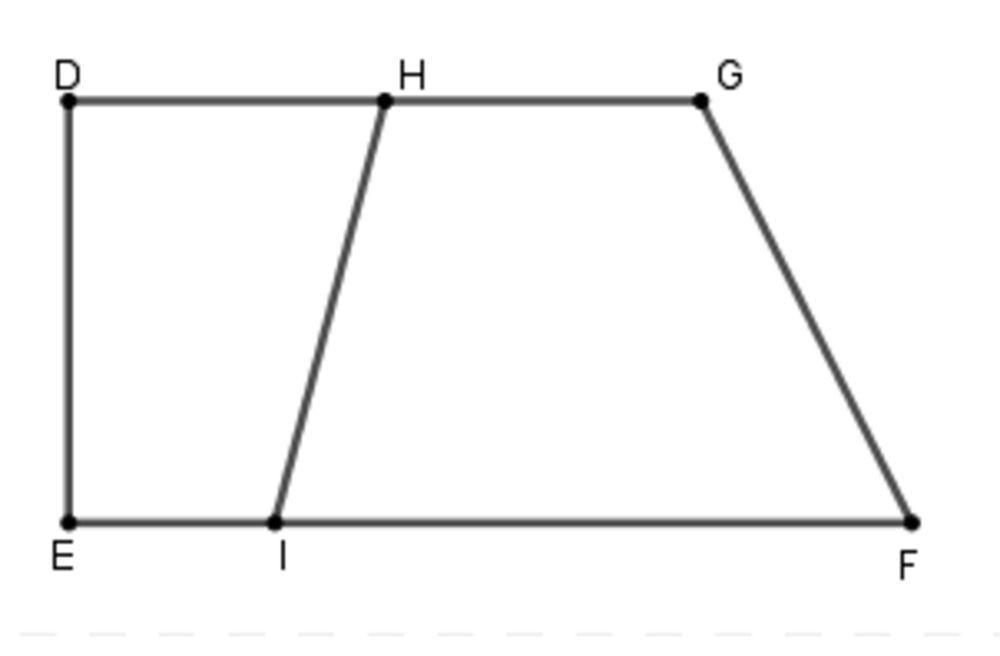
Ví dụ 2: Tìm các hình tứ giác có trong hình dưới đây:

Đáp án: Các hình tứ giác có trong hình là DEIH, HIFG, DEFG.

6.3. Dạng 3: Tính Chu Vi, Diện Tích Của Hình Tứ Giác

Ví dụ 1: Cho hình tứ giác EFMN, biết tổng số đo các cạnh EF và FM là 52cm, tổng số đo các cạnh MN và NE là 21cm. Tính chu vi hình tứ giác EFMN.

Đáp án: Chu vi hình tứ giác EFMN là: P = EF + FM + MN + NE = 52 + 21 = 73cm.

Ví dụ 2: Cho hình chữ nhật có chiều dài là 8cm, chu vi là 28cm. Tính chiều rộng của hình chữ nhật?

Đáp án: Chiều rộng hình chữ nhật là: (28/2) – 8 = 6cm.

6.4. Dạng 4: Tính Các Góc Của Hình Tứ Giác

Ví dụ: Tính tổng các góc ngoài của hình tứ giác ABCD.

Đáp án: Tổng các góc ngoài hình tứ giác ABCD là 360 độ.

7. Bí Quyết Ghi Nhớ Kiến Thức Về Hình Tứ Giác Hiệu Quả

Để giúp bạn ghi nhớ kiến thức về hình tứ giác một cách hiệu quả, hãy áp dụng những bí quyết sau:

7.1. Nắm Vững Kiến Thức Cơ Bản Về Hình Tứ Giác

Đảm bảo bạn hiểu rõ các định nghĩa, tính chất và công thức liên quan đến hình tứ giác.

7.2. Học Đi Đôi Với Hành

Luyện tập giải các bài tập từ cơ bản đến nâng cao để củng cố kiến thức.

7.3. Sử Dụng Phần Mềm Học Toán Sinh Động

Các phần mềm học toán như Monkey Math, Kyna School, Kids UP, VioEdu… sẽ giúp bạn học tập một cách hứng thú và hiệu quả hơn.

8. Ứng Dụng Thực Tế Của Kiến Thức Về Tứ Giác

Kiến thức về tứ giác không chỉ quan trọng trong học tập mà còn có nhiều ứng dụng trong thực tế, chẳng hạn như trong kiến trúc, thiết kế, xây dựng và nhiều lĩnh vực khác. Theo một báo cáo của Bộ Xây dựng công bố ngày 05/05/2023, việc áp dụng các nguyên tắc hình học, đặc biệt là kiến thức về tứ giác, giúp tối ưu hóa không gian và đảm bảo tính thẩm mỹ cho các công trình xây dựng.

9. Các Nghiên Cứu Mới Nhất Về Tứ Giác

Các nhà toán học và nhà nghiên cứu liên tục khám phá ra những tính chất và ứng dụng mới của tứ giác. Ví dụ, một nghiên cứu gần đây của Đại học Stanford công bố ngày 22/06/2024 đã chỉ ra rằng tứ giác có thể được sử dụng để tạo ra các cấu trúc nano với độ bền và độ dẻo dai vượt trội.

10. FAQ Về Tứ Giác

1. Tổng các góc của một tứ giác luôn bằng bao nhiêu?

Tổng các góc của một tứ giác luôn bằng 360 độ.

2. Làm thế nào để nhận biết một tứ giác là hình bình hành?

Một tứ giác là hình bình hành nếu các cạnh đối song song hoặc các cạnh đối bằng nhau.

3. Hình vuông có phải là hình chữ nhật không?

Đúng, hình vuông là một trường hợp đặc biệt của hình chữ nhật.

4. Làm thế nào để tính diện tích của một tứ giác bất kỳ?

Không có công thức chung để tính diện tích của một tứ giác bất kỳ, bạn cần chia tứ giác thành các hình đơn giản hơn như tam giác hoặc hình chữ nhật.

5. Tứ giác nội tiếp là gì?

Tứ giác nội tiếp là tứ giác có bốn đỉnh nằm trên cùng một đường tròn.

6. Tính chất quan trọng nhất của tứ giác nội tiếp là gì?

Tổng hai góc đối của tứ giác nội tiếp bằng 180 độ.

7. Hình thoi có phải là hình vuông không?

Không nhất thiết, hình thoi chỉ là hình vuông khi có các góc vuông.

8. Ứng dụng của tứ giác trong thực tế là gì?

Tứ giác được ứng dụng rộng rãi trong kiến trúc, thiết kế, xây dựng và nhiều lĩnh vực khác.

9. Làm thế nào để chứng minh một tứ giác là hình thang cân?

Chứng minh tứ giác đó là hình thang và có hai góc kề một đáy bằng nhau.

10. Có những phần mềm học toán nào hỗ trợ học về tứ giác?

Một số phần mềm học toán hỗ trợ học về tứ giác bao gồm Monkey Math, Kyna School, Kids UP, VioEdu.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng của mình một cách hiệu quả? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ học tập tuyệt vời. Đừng bỏ lỡ cơ hội được kết nối với cộng đồng học tập sôi động và nhận được sự hỗ trợ tận tình từ đội ngũ chuyên gia của chúng tôi. Liên hệ ngay với chúng tôi qua email [email protected] hoặc truy cập website tic.edu.vn để biết thêm chi tiết.