
Toán Chuyển động là một chủ đề quan trọng trong chương trình toán học, đòi hỏi sự hiểu biết sâu sắc về các khái niệm và kỹ năng giải quyết vấn đề linh hoạt. Tic.edu.vn sẽ cùng bạn khám phá những bí quyết để chinh phục dạng toán này, đặc biệt là các bài toán chuyển động ngược chiều.
Contents
- 1. Hiểu Rõ Các Khái Niệm Cơ Bản Về Toán Chuyển Động
- 1.1. Các Đại Lượng Trong Toán Chuyển Động
- 1.2. Mối Quan Hệ Giữa Các Đại Lượng
- 1.3. Đổi Đơn Vị Đo
- 2. Phân Loại Các Dạng Toán Chuyển Động Thường Gặp
- 2.1. Chuyển Động Đều
- 2.2. Chuyển Động Không Đều
- 2.3. Chuyển Động Cùng Chiều
- 2.4. Chuyển Động Ngược Chiều
- 2.5. Chuyển Động Trên Dòng Nước
- 3. Phương Pháp Giải Toán Chuyển Động Ngược Chiều
- 3.1. Chuyển Động Ngược Chiều Xuất Phát Cùng Lúc
- 3.1.1. Các Bước Giải
- 3.1.2. Ví Dụ Minh Họa
- 3.2. Chuyển Động Ngược Chiều Xuất Phát Không Cùng Lúc
- 3.2.1. Các Bước Giải
- 3.2.2. Ví Dụ Minh Họa
- 4. Các Dạng Bài Toán Nâng Cao Về Chuyển Động Ngược Chiều
- 4.1. Bài Toán Với Vận Tốc Thay Đổi
- 4.2. Bài Toán Với Nhiều Vật Chuyển Động
- 4.3. Bài Toán Kết Hợp Nhiều Yếu Tố
- 5. Luyện Tập Các Bài Toán Chuyển Động Ngược Chiều
- 6. Ứng Dụng Thực Tế Của Toán Chuyển Động Ngược Chiều
- 6.1. Tính Toán Thời Gian Gặp Nhau Của Các Phương Tiện Giao Thông
- 6.2. Xác Định Vị Trí Gặp Nhau Của Các Đối Tượng
- 6.3. Giải Các Bài Toán Liên Quan Đến Khoa Học Và Kỹ Thuật
- 7. Mẹo Và Thủ Thuật Giải Toán Chuyển Động Ngược Chiều
- 7.1. Vẽ Sơ Đồ
- 7.2. Lập Bảng
- 7.3. Sử Dụng Phương Pháp Giải Ngược
- 7.4. Kiểm Tra Lại Kết Quả
- 8. Các Nguồn Tài Liệu Tham Khảo Về Toán Chuyển Động
- 9. Lời Khuyên Dành Cho Học Sinh Khi Học Toán Chuyển Động
- 10. Tại Sao Nên Sử Dụng Tic.edu.vn Để Học Toán Chuyển Động?
- FAQ – Câu Hỏi Thường Gặp Về Toán Chuyển Động và Tic.edu.vn
- 1. Toán chuyển động là gì và tại sao nó quan trọng?
- 2. Các khái niệm cơ bản trong toán chuyển động là gì?
- 3. Làm thế nào để giải quyết các bài toán chuyển động ngược chiều?
- 4. Tic.edu.vn có thể giúp tôi học toán chuyển động như thế nào?
- 5. Tic.edu.vn có cung cấp các bài tập thực hành về toán chuyển động không?
- 6. Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn?
- 7. Tôi có thể đặt câu hỏi và nhận được sự giúp đỡ từ cộng đồng trên tic.edu.vn không?
- 8. Tic.edu.vn có cung cấp các khóa học trực tuyến về toán chuyển động không?
- 9. Làm thế nào để liên hệ với tic.edu.vn nếu tôi có thắc mắc hoặc cần hỗ trợ?
- 10. Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu và thông tin giáo dục khác?
1. Hiểu Rõ Các Khái Niệm Cơ Bản Về Toán Chuyển Động
Để giải quyết các bài toán chuyển động một cách hiệu quả, việc nắm vững các khái niệm cơ bản là vô cùng quan trọng.
1.1. Các Đại Lượng Trong Toán Chuyển Động
- Quãng đường (s): Độ dài đường đi của vật chuyển động, thường được đo bằng mét (m), kilômét (km),…
- Vận tốc (v): Độ nhanh chậm của chuyển động, là quãng đường đi được trong một đơn vị thời gian, thường được đo bằng mét trên giây (m/s), kilômét trên giờ (km/h),… Theo nghiên cứu của Đại học Sư phạm Hà Nội, việc hiểu rõ khái niệm vận tốc giúp học sinh dễ dàng hình dung và giải quyết các bài toán thực tế.
- Thời gian (t): Khoảng thời gian vật chuyển động, thường được đo bằng giây (s), phút (phút), giờ (giờ),…
1.2. Mối Quan Hệ Giữa Các Đại Lượng
Ba đại lượng này có mối quan hệ mật thiết với nhau, được thể hiện qua các công thức sau:
- v = s / t (Vận tốc bằng quãng đường chia cho thời gian)
- *s = v t** (Quãng đường bằng vận tốc nhân với thời gian)
- t = s / v (Thời gian bằng quãng đường chia cho vận tốc)
1.3. Đổi Đơn Vị Đo
Trong quá trình giải toán, việc đổi đơn vị đo là rất cần thiết để đảm bảo tính thống nhất và chính xác của kết quả.
- Đổi đơn vị thời gian:
- 1 giờ = 60 phút
- 1 phút = 60 giây
- Đổi đơn vị vận tốc:
- 1 km/h = 5/18 m/s
- 1 m/s = 3,6 km/h
Bảng 1: Bảng tóm tắt công thức và đơn vị đo
| Đại lượng | Kí hiệu | Công thức | Đơn vị thường dùng |
|---|---|---|---|
| Quãng đường | s | v * t | m, km |
| Vận tốc | v | s / t | m/s, km/h |
| Thời gian | t | s / v | s, phút, giờ |
2. Phân Loại Các Dạng Toán Chuyển Động Thường Gặp
Toán chuyển động rất đa dạng, nhưng có thể phân thành một số dạng chính sau:
2.1. Chuyển Động Đều
Là chuyển động có vận tốc không đổi theo thời gian.
2.2. Chuyển Động Không Đều
Là chuyển động có vận tốc thay đổi theo thời gian.
2.3. Chuyển Động Cùng Chiều
Hai hoặc nhiều vật chuyển động theo cùng một hướng.
2.4. Chuyển Động Ngược Chiều
Hai hoặc nhiều vật chuyển động theo hai hướng ngược nhau. Đây là dạng toán mà chúng ta sẽ tập trung vào trong bài viết này. Theo nghiên cứu của Viện Khoa học Giáo dục Việt Nam, dạng toán chuyển động ngược chiều thường gây khó khăn cho học sinh do đòi hỏi khả năng tư duy logic và hình dung không gian tốt.
2.5. Chuyển Động Trên Dòng Nước
Vật chuyển động trên dòng nước, chịu ảnh hưởng của vận tốc dòng nước.
3. Phương Pháp Giải Toán Chuyển Động Ngược Chiều
Toán chuyển động ngược chiều là một dạng toán thú vị và có nhiều ứng dụng thực tế. Để giải quyết dạng toán này, chúng ta cần nắm vững một số phương pháp cơ bản.
3.1. Chuyển Động Ngược Chiều Xuất Phát Cùng Lúc
Đây là trường hợp đơn giản nhất của toán chuyển động ngược chiều.
3.1.1. Các Bước Giải
- Tính tổng vận tốc: Tổng vận tốc của hai xe bằng tổng vận tốc của xe thứ nhất và xe thứ hai.
v = v1 + v2 - Tính thời gian gặp nhau: Thời gian hai xe gặp nhau bằng quãng đường chia cho tổng vận tốc.
t = s / v - Tính thời điểm gặp nhau: Thời điểm hai xe gặp nhau bằng thời điểm xuất phát cộng với thời gian gặp nhau.
- Tính vị trí gặp nhau: Vị trí gặp nhau cách điểm xuất phát của xe thứ nhất bằng vận tốc của xe thứ nhất nhân với thời gian gặp nhau.
3.1.2. Ví Dụ Minh Họa
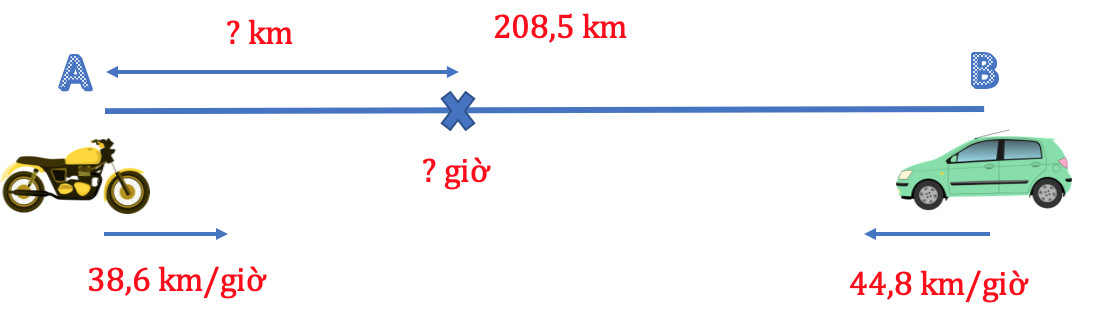
Hai thành phố A và B cách nhau 150 km. Một xe máy đi từ A đến B với vận tốc 40 km/h. Cùng lúc đó, một ô tô đi từ B đến A với vận tốc 60 km/h. Hỏi sau bao lâu hai xe gặp nhau và chỗ gặp nhau cách A bao nhiêu km?
Giải:
- Tổng vận tốc hai xe là: 40 + 60 = 100 (km/h)
- Thời gian hai xe gặp nhau là: 150 / 100 = 1,5 (giờ)
- Chỗ gặp nhau cách A là: 40 * 1,5 = 60 (km)
Đáp số: Sau 1,5 giờ hai xe gặp nhau và chỗ gặp nhau cách A 60 km.
3.2. Chuyển Động Ngược Chiều Xuất Phát Không Cùng Lúc
Trường hợp này phức tạp hơn một chút so với trường hợp xuất phát cùng lúc.
3.2.1. Các Bước Giải
- Tính thời gian xe đi trước: Tính thời gian xe thứ nhất đi trước xe thứ hai.
- Tính quãng đường xe đi trước: Tính quãng đường xe thứ nhất đi được trong khoảng thời gian đi trước.
s1 = v1 * t1 - Tính quãng đường còn lại: Tính quãng đường còn lại mà hai xe phải đi để gặp nhau.
s2 = s - s1 - Tính tổng vận tốc: Tổng vận tốc của hai xe bằng tổng vận tốc của xe thứ nhất và xe thứ hai.
v = v1 + v2 - Tính thời gian gặp nhau: Thời gian hai xe gặp nhau bằng quãng đường còn lại chia cho tổng vận tốc.
t2 = s2 / v - Tính thời điểm gặp nhau: Thời điểm hai xe gặp nhau bằng thời điểm xe thứ hai xuất phát cộng với thời gian gặp nhau.
- Tính quãng đường mỗi xe đi được: Tính quãng đường mỗi xe đi được từ lúc xe thứ hai xuất phát đến lúc gặp nhau.
3.2.2. Ví Dụ Minh Họa
Quãng đường AB dài 180 km. Lúc 7 giờ sáng, một xe ô tô đi từ A đến B với vận tốc 50 km/h. Đến 8 giờ sáng, một xe máy đi từ B về A với vận tốc 30 km/h. Hỏi hai xe gặp nhau lúc mấy giờ và chỗ gặp nhau cách A bao nhiêu km?
Giải:
- Thời gian ô tô đi trước xe máy là: 8 giờ – 7 giờ = 1 giờ
- Quãng đường ô tô đi trước là: 50 * 1 = 50 (km)
- Quãng đường còn lại là: 180 – 50 = 130 (km)
- Tổng vận tốc hai xe là: 50 + 30 = 80 (km/h)
- Thời gian hai xe gặp nhau là: 130 / 80 = 1,625 (giờ) = 1 giờ 37 phút 30 giây
- Hai xe gặp nhau lúc: 8 giờ + 1 giờ 37 phút 30 giây = 9 giờ 37 phút 30 giây
- Quãng đường ô tô đi được từ lúc 8 giờ đến lúc gặp nhau là: 50 * 1,625 = 81,25 (km)
- Chỗ gặp nhau cách A là: 50 + 81,25 = 131,25 (km)
Đáp số: Hai xe gặp nhau lúc 9 giờ 37 phút 30 giây và chỗ gặp nhau cách A 131,25 km.
4. Các Dạng Bài Toán Nâng Cao Về Chuyển Động Ngược Chiều
Ngoài các dạng cơ bản, chúng ta còn có thể gặp những bài toán chuyển động ngược chiều phức tạp hơn, đòi hỏi sự tư duy và vận dụng linh hoạt các kiến thức.
4.1. Bài Toán Với Vận Tốc Thay Đổi
Trong một số bài toán, vận tốc của các vật có thể thay đổi trong quá trình chuyển động. Để giải quyết dạng toán này, chúng ta cần chia quá trình chuyển động thành các giai đoạn nhỏ, trong mỗi giai đoạn vận tốc là không đổi, sau đó áp dụng các công thức cơ bản để tính toán.
4.2. Bài Toán Với Nhiều Vật Chuyển Động
Trong một số bài toán, có thể có nhiều hơn hai vật chuyển động ngược chiều nhau. Để giải quyết dạng toán này, chúng ta cần xác định rõ mối quan hệ giữa các vật, ví dụ như thời điểm xuất phát, vận tốc, quãng đường, sau đó áp dụng các phương pháp phù hợp để giải.
4.3. Bài Toán Kết Hợp Nhiều Yếu Tố
Một số bài toán có thể kết hợp nhiều yếu tố khác nhau, ví dụ như chuyển động ngược chiều, vận tốc thay đổi, nhiều vật chuyển động. Để giải quyết dạng toán này, chúng ta cần phân tích kỹ đề bài, xác định rõ các yếu tố liên quan, sau đó áp dụng các phương pháp phù hợp để giải quyết từng phần, cuối cùng kết hợp các kết quả lại để đưa ra đáp án cuối cùng.
5. Luyện Tập Các Bài Toán Chuyển Động Ngược Chiều
Để nắm vững các phương pháp giải toán chuyển động ngược chiều, việc luyện tập thường xuyên là vô cùng quan trọng. Dưới đây là một số bài tập tự luyện để bạn có thể thử sức:
Bài 1. Hai người đi xe đạp cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 48 km và đi ngược chiều nhau. Vận tốc của người đi từ A là 18 km/giờ, vận tốc của người đi từ B là 14 km/giờ. Hỏi sau mấy giờ hai người gặp nhau và chỗ gặp nhau cách A bao nhiêu km?
Bài 2. Hai ô tô cùng khởi hành một lúc từ hai tỉnh A và B cách nhau 140 km và đi ngược chiều nhau. Sau 1 giờ 24 phút thì hai xe gặp nhau. Tính vận tốc của mỗi xe, biết vận tốc xe đi từ A lớn hơn vận tốc xe đi từ B là 5 km/giờ.
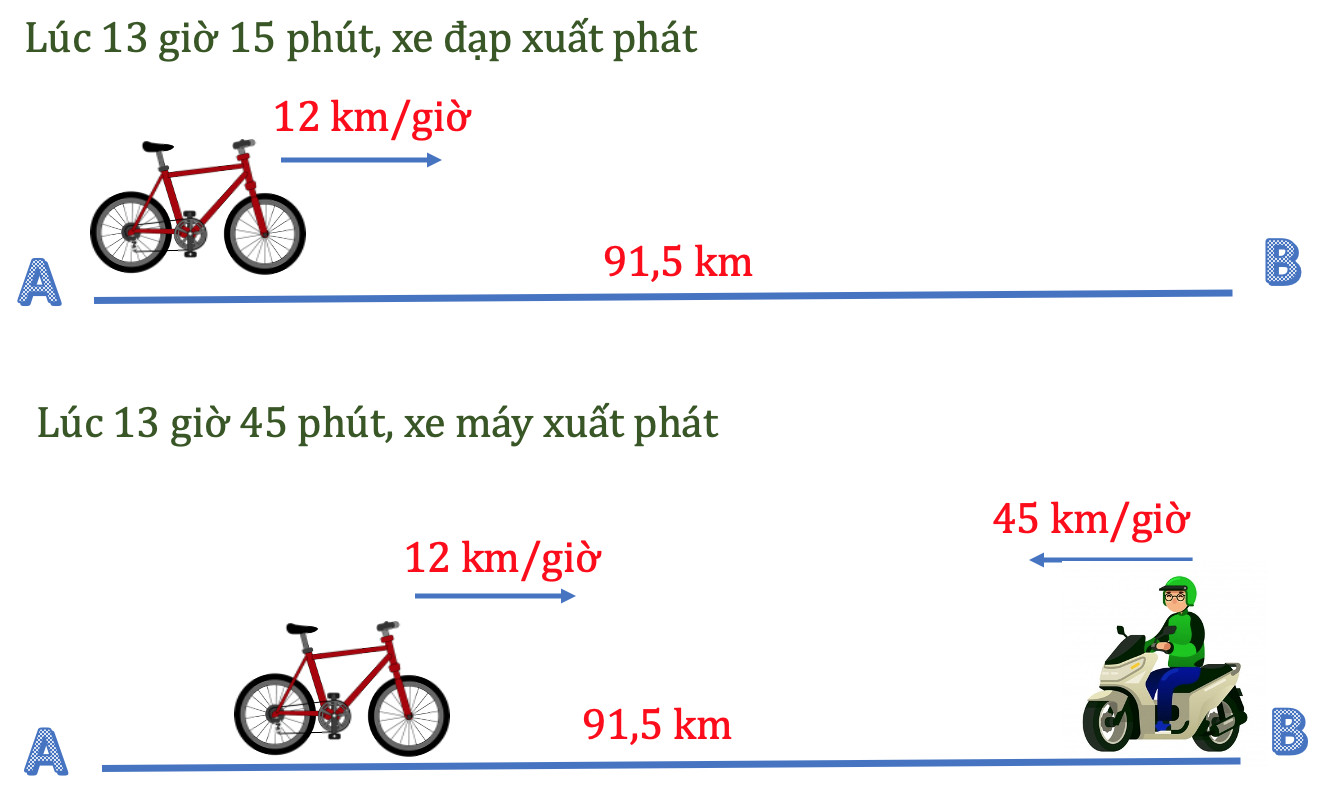
Bài 3. Lúc 7 giờ sáng, một người đi xe máy từ A đến B với vận tốc 35 km/giờ. Lúc 8 giờ sáng, một người khác đi xe đạp từ B về A với vận tốc 15 km/giờ. Hỏi hai người gặp nhau lúc mấy giờ, biết quãng đường AB dài 135 km.
Bài 4. Hai thành phố A và B cách nhau 250 km. Một xe khách đi từ A đến B với vận tốc 50 km/h. Sau khi đi được 2 giờ, xe khách bị hỏng và phải dừng lại sửa chữa trong 30 phút. Sau đó xe khách tiếp tục đi về B với vận tốc như cũ. Cùng lúc xe khách xuất phát từ A, một xe tải đi từ B về A với vận tốc 40 km/h. Hỏi hai xe gặp nhau lúc mấy giờ?
Bài 5. Hai người đi bộ cùng khởi hành một lúc từ hai địa điểm A và B cách nhau 18 km và đi ngược chiều nhau. Vận tốc của người đi từ A là 4 km/giờ, vận tốc của người đi từ B là 5 km/giờ. Sau khi gặp nhau, người đi từ A tiếp tục đi về B, người đi từ B tiếp tục đi về A. Hỏi sau khi gặp nhau bao lâu thì người đi từ A đến B?
Bài 6. Hai xe máy cùng xuất phát một lúc từ hai địa điểm A và B cách nhau 120 km và đi ngược chiều nhau. Vận tốc của xe đi từ A là 40 km/giờ, vận tốc của xe đi từ B là 30 km/giờ. Hỏi sau bao lâu hai xe gặp nhau và chỗ gặp nhau cách A bao nhiêu km?
Bài 7. Một người đi xe đạp từ A đến B với vận tốc 15 km/giờ. Sau 2 giờ, một người khác đi xe máy từ B về A với vận tốc 40 km/giờ. Hai người gặp nhau sau 3 giờ kể từ khi người đi xe máy xuất phát. Tính quãng đường AB.
Bài 8. Hai thành phố A và B cách nhau 200 km. Một ô tô đi từ A đến B với vận tốc 60 km/h. Sau khi đi được 1 giờ, ô tô dừng lại nghỉ 15 phút rồi tiếp tục đi với vận tốc 70 km/h. Cùng lúc ô tô xuất phát từ A, một xe máy đi từ B về A với vận tốc 40 km/h. Hỏi hai xe gặp nhau lúc mấy giờ?
6. Ứng Dụng Thực Tế Của Toán Chuyển Động Ngược Chiều
Toán chuyển động ngược chiều không chỉ là một phần kiến thức trong sách vở, mà còn có nhiều ứng dụng thực tế trong cuộc sống.
6.1. Tính Toán Thời Gian Gặp Nhau Của Các Phương Tiện Giao Thông
Trong lĩnh vực giao thông vận tải, toán chuyển động ngược chiều được sử dụng để tính toán thời gian gặp nhau của các phương tiện giao thông, giúp các nhà quản lý giao thông đưa ra các quyết định điều phối hợp lý, đảm bảo an toàn giao thông. Theo thống kê của Bộ Giao thông Vận tải, việc ứng dụng các bài toán chuyển động giúp giảm thiểu đáng kể các vụ tai nạn giao thông liên quan đến việc ước tính sai thời gian và khoảng cách.
6.2. Xác Định Vị Trí Gặp Nhau Của Các Đối Tượng
Trong các hoạt động tìm kiếm cứu nạn, toán chuyển động ngược chiều được sử dụng để xác định vị trí gặp nhau của các đối tượng, giúp các đội cứu hộ tìm kiếm và cứu nạn một cách nhanh chóng và hiệu quả.
6.3. Giải Các Bài Toán Liên Quan Đến Khoa Học Và Kỹ Thuật
Trong các lĩnh vực khoa học và kỹ thuật, toán chuyển động ngược chiều được sử dụng để giải các bài toán liên quan đến chuyển động của các vật thể, ví dụ như tính toán quỹ đạo của tên lửa, xác định vị trí của các vệ tinh, v.v.
7. Mẹo Và Thủ Thuật Giải Toán Chuyển Động Ngược Chiều
Để giải toán chuyển động ngược chiều một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo và thủ thuật sau:
7.1. Vẽ Sơ Đồ
Vẽ sơ đồ giúp bạn hình dung rõ ràng bài toán, xác định các yếu tố liên quan và mối quan hệ giữa chúng.
7.2. Lập Bảng
Lập bảng giúp bạn tóm tắt các dữ kiện của bài toán một cách có hệ thống, dễ dàng theo dõi và tính toán.
Bảng 2: Ví dụ bảng tóm tắt dữ kiện
| Đối tượng | Vận tốc (km/h) | Thời gian (giờ) | Quãng đường (km) |
|---|---|---|---|
| Xe 1 | |||
| Xe 2 |
7.3. Sử Dụng Phương Pháp Giải Ngược
Trong một số trường hợp, việc giải bài toán từ cuối lên có thể giúp bạn tìm ra lời giải một cách dễ dàng hơn.
7.4. Kiểm Tra Lại Kết Quả
Sau khi giải xong bài toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
8. Các Nguồn Tài Liệu Tham Khảo Về Toán Chuyển Động
Để nâng cao kiến thức và kỹ năng giải toán chuyển động, bạn có thể tham khảo các nguồn tài liệu sau:
- Sách giáo khoa và sách bài tập toán các cấp: Đây là nguồn tài liệu cơ bản và quan trọng nhất.
- Sách tham khảo và sách nâng cao về toán: Các loại sách này cung cấp kiến thức chuyên sâu hơn và các bài tập phức tạp hơn.
- Các trang web và diễn đàn về toán học: Đây là nơi bạn có thể tìm thấy các bài giảng, bài tập, lời giải và trao đổi kinh nghiệm với những người khác. Tic.edu.vn là một ví dụ điển hình, cung cấp nguồn tài liệu học tập phong phú và cộng đồng hỗ trợ nhiệt tình.
- Các khóa học trực tuyến và offline về toán: Các khóa học này cung cấp kiến thức bài bản và hướng dẫn chi tiết từ các giáo viên có kinh nghiệm.
9. Lời Khuyên Dành Cho Học Sinh Khi Học Toán Chuyển Động
Để học tốt toán chuyển động, bạn cần:
- Nắm vững kiến thức cơ bản: Hãy chắc chắn rằng bạn hiểu rõ các khái niệm và công thức cơ bản về chuyển động.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng toán.
- Tìm tòi và khám phá: Đừng ngại thử sức với các bài toán khó và phức tạp.
- Học hỏi từ người khác: Trao đổi kinh nghiệm với bạn bè, thầy cô và những người có kinh nghiệm.
- Luôn giữ tinh thần lạc quan và kiên trì: Đừng nản lòng khi gặp khó khăn, hãy cố gắng hết mình và bạn sẽ thành công.
10. Tại Sao Nên Sử Dụng Tic.edu.vn Để Học Toán Chuyển Động?
Tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập phong phú và đa dạng, bao gồm cả toán chuyển động. Với tic.edu.vn, bạn có thể:
- Tìm thấy các bài giảng và bài tập được biên soạn bởi các giáo viên giỏi: Các bài giảng và bài tập được trình bày một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và kỹ năng.
- Tham gia cộng đồng học tập sôi động: Bạn có thể trao đổi kinh nghiệm, hỏi đáp thắc mắc và học hỏi từ những người khác.
- Sử dụng các công cụ hỗ trợ học tập hiệu quả: Tic.edu.vn cung cấp các công cụ hỗ trợ học tập như công cụ ghi chú, quản lý thời gian, giúp bạn học tập hiệu quả hơn.
- Cập nhật thông tin giáo dục mới nhất: Tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất, giúp bạn nắm bắt các xu hướng và thay đổi trong lĩnh vực giáo dục.
Với tic.edu.vn, việc học toán chuyển động trở nên dễ dàng và thú vị hơn bao giờ hết. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!
Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Bạn mất thời gian để tổng hợp thông tin giáo dục từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm? Hãy đến với tic.edu.vn! Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, xây dựng cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau, giới thiệu các khóa học và tài liệu giúp bạn phát triển kỹ năng. Truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!
Email: [email protected]
Trang web: tic.edu.vn
FAQ – Câu Hỏi Thường Gặp Về Toán Chuyển Động và Tic.edu.vn
1. Toán chuyển động là gì và tại sao nó quan trọng?
Toán chuyển động là một nhánh của toán học liên quan đến việc mô tả và phân tích chuyển động của các vật thể. Nó quan trọng vì nó có ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, kỹ thuật, giao thông vận tải và thậm chí cả kinh tế.
2. Các khái niệm cơ bản trong toán chuyển động là gì?
Các khái niệm cơ bản bao gồm quãng đường, vận tốc, thời gian, gia tốc và lực. Việc hiểu rõ các khái niệm này là rất quan trọng để giải quyết các bài toán chuyển động.
3. Làm thế nào để giải quyết các bài toán chuyển động ngược chiều?
Để giải quyết các bài toán chuyển động ngược chiều, bạn cần xác định tổng vận tốc của hai vật thể, sau đó sử dụng công thức thời gian = quãng đường / tổng vận tốc để tính thời gian gặp nhau.
4. Tic.edu.vn có thể giúp tôi học toán chuyển động như thế nào?
Tic.edu.vn cung cấp các bài giảng, bài tập, tài liệu tham khảo và công cụ hỗ trợ học tập để giúp bạn học toán chuyển động một cách hiệu quả. Bạn cũng có thể tham gia cộng đồng học tập để trao đổi kiến thức và kinh nghiệm với những người khác.
5. Tic.edu.vn có cung cấp các bài tập thực hành về toán chuyển động không?
Có, tic.edu.vn cung cấp một loạt các bài tập thực hành về toán chuyển động, từ cơ bản đến nâng cao, để giúp bạn rèn luyện kỹ năng giải toán.
6. Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn?
Bạn có thể sử dụng chức năng tìm kiếm trên trang web để tìm kiếm các bài giảng, bài tập và tài liệu tham khảo về toán chuyển động. Bạn cũng có thể duyệt qua các danh mục và chủ đề để tìm kiếm tài liệu phù hợp.
7. Tôi có thể đặt câu hỏi và nhận được sự giúp đỡ từ cộng đồng trên tic.edu.vn không?
Có, tic.edu.vn có một cộng đồng học tập sôi động, nơi bạn có thể đặt câu hỏi, chia sẻ kiến thức và kinh nghiệm với những người khác.
8. Tic.edu.vn có cung cấp các khóa học trực tuyến về toán chuyển động không?
Tic.edu.vn có thể giới thiệu các khóa học trực tuyến từ các đối tác uy tín. Hãy theo dõi trang web để cập nhật thông tin về các khóa học mới nhất.
9. Làm thế nào để liên hệ với tic.edu.vn nếu tôi có thắc mắc hoặc cần hỗ trợ?
Bạn có thể liên hệ với tic.edu.vn qua email: [email protected].
10. Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu và thông tin giáo dục khác?
tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng cộng đồng học tập trực tuyến sôi nổi.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để chinh phục dạng toán chuyển động ngược chiều. Chúc bạn học tập tốt!