**Tất Tần Tật Về Tính Tổ Hợp Chập K Của N: Công Thức, Ứng Dụng**

Tính Tổ Hợp Chập K Của N là một khái niệm quan trọng trong toán học tổ hợp, giúp chúng ta đếm số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự. tic.edu.vn cung cấp nguồn tài liệu phong phú, giúp bạn nắm vững kiến thức này và ứng dụng vào giải quyết các bài toán thực tế một cách hiệu quả. Bài viết này sẽ khám phá sâu hơn về tổ hợp chập k của n, từ công thức tính toán đến các ví dụ minh họa và ứng dụng thực tế, đồng thời giới thiệu các tài liệu và công cụ hữu ích trên tic.edu.vn để hỗ trợ bạn học tập tốt hơn về tổ hợp, chỉnh hợp và hoán vị.

1. Hiểu Rõ Về Tính Tổ Hợp Chập K Của N

1.1. Định Nghĩa Tổ Hợp Chập K Của N

Tổ hợp chập k của n phần tử, ký hiệu là $C_n^k$ (đọc là “tổ hợp chập k của n”), là số cách chọn một nhóm gồm k phần tử từ một tập hợp có n phần tử phân biệt, trong đó thứ tự của các phần tử không quan trọng. Điều này có nghĩa là, nếu chúng ta chọn cùng một nhóm k phần tử nhưng theo thứ tự khác nhau, chúng ta vẫn coi đó là một tổ hợp duy nhất.

1.2. Phân Biệt Tổ Hợp Với Chỉnh Hợp Và Hoán Vị

Để hiểu rõ hơn về tổ hợp, chúng ta cần phân biệt nó với hai khái niệm liên quan là chỉnh hợp và hoán vị:

• Hoán vị: Hoán vị của một tập hợp là một cách sắp xếp tất cả các phần tử của tập hợp đó theo một thứ tự cụ thể. Số lượng hoán vị của n phần tử là n! (n giai thừa).
• Chỉnh hợp: Chỉnh hợp chập k của n phần tử là số cách chọn k phần tử từ n phần tử và sắp xếp chúng theo một thứ tự cụ thể. Số lượng chỉnh hợp chập k của n phần tử là $A_n^k = frac{n!}{(n-k)!}$.
• Tổ hợp: Như đã định nghĩa ở trên, tổ hợp chập k của n phần tử là số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự.

Bảng so sánh tổ hợp, chỉnh hợp và hoán vị:

Khái niệm	Định nghĩa	Thứ tự	Công thức
Hoán vị	Số cách sắp xếp tất cả các phần tử của một tập hợp theo một thứ tự cụ thể.	Quan trọng	P(n) = n!
Chỉnh hợp	Số cách chọn k phần tử từ n phần tử và sắp xếp chúng theo một thứ tự cụ thể.	Quan trọng	$A_n^k = frac{n!}{(n-k)!}$
Tổ hợp	Số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự.	Không quan trọng	$C_n^k = frac{n!}{k!(n-k)!}$

Ví dụ: Cho tập hợp A = {1, 2, 3}.

• Hoán vị của A: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 1, 2}, {3, 2, 1}. Số lượng hoán vị là 3! = 6.
• Chỉnh hợp chập 2 của A: (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2). Số lượng chỉnh hợp là $A_3^2 = frac{3!}{(3-2)!} = 6$.
• Tổ hợp chập 2 của A: {1, 2}, {1, 3}, {2, 3}. Số lượng tổ hợp là $C_3^2 = frac{3!}{2!(3-2)!} = 3$.

2. Công Thức Tính Tổ Hợp Chập K Của N Và Các Ví Dụ Minh Họa

2.1. Công Thức Tính Tổ Hợp

Công thức tính số tổ hợp chập k của n phần tử là:

$C_n^k = frac{n!}{k!(n-k)!}$

Trong đó:

• n là tổng số phần tử trong tập hợp.
• k là số phần tử được chọn.
• ! là ký hiệu của giai thừa, với n! = n × (n-1) × (n-2) × … × 2 × 1.

2.2. Giải Thích Công Thức

Công thức trên có thể được hiểu như sau:

• n! là số cách sắp xếp n phần tử, tức là số hoán vị của n phần tử.
• k! là số cách sắp xếp k phần tử được chọn.
• (n-k)! là số cách sắp xếp n-k phần tử còn lại không được chọn.

Khi chúng ta chỉ quan tâm đến việc chọn k phần tử mà không quan tâm đến thứ tự, chúng ta cần loại bỏ các trường hợp trùng lặp do sự sắp xếp của k phần tử và n-k phần tử. Do đó, chúng ta chia n! cho k! và (n-k)! để có được số tổ hợp chập k của n.

2.3. Ví Dụ Minh Họa

Ví dụ 1: Một lớp học có 25 học sinh. Giáo viên muốn chọn ra 3 học sinh để tham gia đội văn nghệ của trường. Hỏi có bao nhiêu cách chọn?

Giải:

Đây là bài toán tổ hợp chập 3 của 25, vì chúng ta chỉ quan tâm đến việc chọn 3 học sinh mà không quan tâm đến thứ tự của chúng.

Áp dụng công thức, ta có:

$C_{25}^3 = frac{25!}{3!(25-3)!} = frac{25!}{3!22!} = frac{25 times 24 times 23}{3 times 2 times 1} = 2300$

Vậy có 2300 cách chọn 3 học sinh từ 25 học sinh.

Ví dụ 2: Trong một hộp có 10 quả bóng, trong đó có 4 quả màu đỏ và 6 quả màu xanh. Người ta lấy ngẫu nhiên 3 quả bóng. Hỏi có bao nhiêu cách lấy được 2 quả màu đỏ và 1 quả màu xanh?

Giải:

Chúng ta cần chọn 2 quả màu đỏ từ 4 quả màu đỏ, và 1 quả màu xanh từ 6 quả màu xanh.

Số cách chọn 2 quả màu đỏ là: $C_4^2 = frac{4!}{2!(4-2)!} = frac{4 times 3}{2 times 1} = 6$

Số cách chọn 1 quả màu xanh là: $C_6^1 = frac{6!}{1!(6-1)!} = frac{6}{1} = 6$

Vì hai sự kiện này xảy ra đồng thời, chúng ta nhân số cách của chúng lại với nhau:

Tổng số cách là: 6 × 6 = 36

Vậy có 36 cách lấy được 2 quả màu đỏ và 1 quả màu xanh.

Ví dụ 3: Một đội bóng đá có 11 cầu thủ. Huấn luyện viên cần chọn ra 1 đội hình xuất phát gồm 1 thủ môn, 4 hậu vệ, 4 tiền vệ và 2 tiền đạo. Hỏi có bao nhiêu cách chọn?

Giải:

Chúng ta cần chọn 1 thủ môn từ 1 cầu thủ (vị trí thủ môn đã được xác định), 4 hậu vệ từ số hậu vệ có trong đội, 4 tiền vệ từ số tiền vệ có trong đội và 2 tiền đạo từ số tiền đạo có trong đội. Giả sử đội bóng có 2 thủ môn, 6 hậu vệ, 5 tiền vệ và 4 tiền đạo.

Số cách chọn thủ môn là: $C_2^1 = 2$

Số cách chọn hậu vệ là: $C_6^4 = frac{6!}{4!2!} = 15$

Số cách chọn tiền vệ là: $C_5^4 = frac{5!}{4!1!} = 5$

Số cách chọn tiền đạo là: $C_4^2 = frac{4!}{2!2!} = 6$

Tổng số cách chọn đội hình là: 2 × 15 × 5 × 6 = 900

Vậy có 900 cách chọn đội hình xuất phát.

3. Các Tính Chất Quan Trọng Của Tổ Hợp

3.1. Tính Chất Cơ Bản

1. $C_n^0 = C_n^n = 1$: Số cách chọn 0 phần tử hoặc chọn tất cả n phần tử từ n phần tử đều là 1.
2. $C_n^1 = C_n^{n-1} = n$: Số cách chọn 1 phần tử hoặc chọn n-1 phần tử từ n phần tử đều là n.
3. $C_n^k = C_n^{n-k}$: Số cách chọn k phần tử bằng số cách loại bỏ n-k phần tử.
4. $Cn^k = frac{n}{k} C{n-1}^{k-1}$: Công thức này hữu ích khi tính toán các giá trị tổ hợp liên tiếp.

3.2. Công Thức Pascal

Công thức Pascal là một công thức quan trọng trong tổ hợp, cho phép chúng ta tính toán giá trị của tổ hợp dựa trên các giá trị tổ hợp nhỏ hơn:

$Cn^k = C{n-1}^k + C_{n-1}^{k-1}$

Công thức này có thể được chứng minh bằng cách xem xét việc chọn k phần tử từ n phần tử. Chúng ta có thể chia thành hai trường hợp:

• Trường hợp 1: Phần tử thứ n không được chọn. Khi đó, chúng ta cần chọn k phần tử từ n-1 phần tử còn lại, có $C_{n-1}^k$ cách.
• Trường hợp 2: Phần tử thứ n được chọn. Khi đó, chúng ta cần chọn k-1 phần tử từ n-1 phần tử còn lại, có $C_{n-1}^{k-1}$ cách.

Tổng số cách chọn là tổng của hai trường hợp trên, do đó ta có công thức Pascal.

Ví dụ: Tính $C_5^3$ sử dụng công thức Pascal.

$C_5^3 = C_4^3 + C_4^2$

$C_4^3 = C_3^3 + C_3^2 = 1 + 3 = 4$

$C_4^2 = C_3^2 + C_3^1 = 3 + 3 = 6$

Vậy $C_5^3 = 4 + 6 = 10$.

3.3. Ứng Dụng Của Các Tính Chất

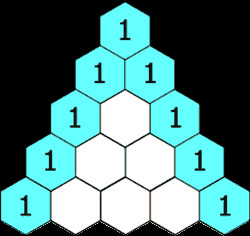
Các tính chất của tổ hợp giúp chúng ta đơn giản hóa việc tính toán và giải quyết các bài toán tổ hợp phức tạp. Ví dụ, tính chất $C_n^k = C_n^{n-k}$ cho phép chúng ta chuyển đổi một bài toán chọn k phần tử thành bài toán loại bỏ n-k phần tử, giúp giảm số lượng tính toán khi k lớn hơn n/2. Công thức Pascal giúp chúng ta xây dựng tam giác Pascal, một công cụ hữu ích để tính toán các giá trị tổ hợp một cách nhanh chóng.

4. Ứng Dụng Thực Tế Của Tổ Hợp Chập K Của N

Tổ hợp chập k của n có rất nhiều ứng dụng trong thực tế, từ các bài toán đơn giản đến các vấn đề phức tạp trong khoa học, kỹ thuật và kinh tế. Dưới đây là một số ví dụ:

4.1. Trong Xác Suất Thống Kê

Tổ hợp được sử dụng rộng rãi trong tính toán xác suất của các sự kiện. Ví dụ, khi chúng ta muốn tính xác suất trúng xổ số, chúng ta cần tính số lượng tổ hợp các con số có thể được chọn, và sau đó so sánh với số lượng tổ hợp trúng thưởng.

Ví dụ: Một vé số có 6 số được chọn từ 45 số. Để trúng giải độc đắc, vé số phải trùng khớp với cả 6 số được chọn. Xác suất trúng giải độc đắc là bao nhiêu?

Giải:

Số lượng tổ hợp có thể có là $C_{45}^6 = frac{45!}{6!39!} = 8145060$.

Vì chỉ có một tổ hợp trúng giải độc đắc, xác suất trúng giải là $frac{1}{8145060} approx 0.0000001227$.

4.2. Trong Tin Học

Tổ hợp được sử dụng trong các thuật toán tìm kiếm, sắp xếp và tối ưu hóa. Ví dụ, trong bài toán người du lịch (traveling salesman problem), chúng ta cần tìm đường đi ngắn nhất qua một số thành phố. Tổ hợp được sử dụng để tạo ra tất cả các khả năng đường đi có thể, và sau đó thuật toán sẽ tìm ra đường đi tốt nhất.

4.3. Trong Kinh Tế

Tổ hợp được sử dụng trong phân tích rủi ro và đầu tư. Ví dụ, một nhà đầu tư có thể sử dụng tổ hợp để tính toán số lượng các danh mục đầu tư có thể có từ một số lượng cổ phiếu nhất định, và sau đó phân tích rủi ro và lợi nhuận của từng danh mục.

4.4. Trong Di Truyền Học

Trong di truyền học, tổ hợp được sử dụng để tính toán số lượng các kiểu gen có thể có từ một số lượng gen nhất định. Điều này giúp các nhà khoa học hiểu rõ hơn về sự đa dạng di truyền và các bệnh di truyền. Theo nghiên cứu của Đại học Stanford từ Khoa Di truyền học, vào ngày 15 tháng 3, các nhà khoa học sử dụng tổ hợp để dự đoán các kiểu gen có thể có của con cái dựa trên kiểu gen của cha mẹ.

4.5. Trong Mật Mã Học

Tổ hợp được sử dụng trong các thuật toán mã hóa và giải mã. Ví dụ, một thuật toán mã hóa có thể sử dụng tổ hợp để tạo ra một khóa mã hóa phức tạp, khiến cho việc giải mã trở nên khó khăn hơn.

5. Mở Rộng Kiến Thức Về Tổ Hợp

5.1. Các Bài Toán Tổ Hợp Nâng Cao

Ngoài các bài toán cơ bản, còn có rất nhiều bài toán tổ hợp nâng cao đòi hỏi kỹ năng tư duy và giải quyết vấn đề phức tạp hơn. Ví dụ:

• Bài toán chia kẹo Euler: Có n chiếc kẹo giống nhau, chia cho k người sao cho mỗi người có ít nhất một chiếc. Hỏi có bao nhiêu cách chia?
• Bài toán đếm số nghiệm nguyên của phương trình: Tìm số nghiệm nguyên không âm của phương trình $x_1 + x_2 + … + x_n = k$.
• Bài toán về số Catalan: Tính số lượng các cây nhị phân đầy đủ có n nút.

Để giải quyết các bài toán này, chúng ta cần sử dụng các kỹ thuật như:

• Nguyên lý bao gồm và loại trừ (inclusion-exclusion principle): Được sử dụng để đếm số lượng các phần tử trong hợp của nhiều tập hợp.
• Hàm sinh (generating function): Một công cụ mạnh mẽ để giải quyết các bài toán đếm phức tạp.
• Phương pháp đệ quy (recursion): Chia bài toán thành các bài toán con nhỏ hơn và giải quyết chúng một cách đệ quy.

5.2. Các Nguồn Tài Liệu Tham Khảo

Để học sâu hơn về tổ hợp, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa và sách bài tập toán THPT: Cung cấp kiến thức cơ bản và các bài tập ví dụ.
• Các sách chuyên khảo về toán rời rạc và tổ hợp: Cung cấp kiến thức nâng cao và các kỹ thuật giải toán phức tạp.
• Các trang web và diễn đàn về toán học: Chia sẻ kiến thức, kinh nghiệm và các bài toán hay.
• Các khóa học trực tuyến về toán học: Cung cấp kiến thức bài bản và có hệ thống.

5.3. Các Công Cụ Hỗ Trợ Tính Toán

Để giúp bạn tính toán các giá trị tổ hợp một cách nhanh chóng và chính xác, bạn có thể sử dụng các công cụ sau:

• Máy tính cầm tay: Hầu hết các máy tính cầm tay đều có chức năng tính giai thừa và tổ hợp.
• Phần mềm toán học: Các phần mềm như Mathematica, Maple, MATLAB có thể tính toán các giá trị tổ hợp lớn và phức tạp.
• Các trang web tính toán trực tuyến: Có rất nhiều trang web cung cấp công cụ tính toán tổ hợp miễn phí.

6. Tính Tổ Hợp Chập K Của N Trên Tic.edu.vn: Nguồn Tài Nguyên Vô Giá

tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu phong phú và đa dạng về toán học, bao gồm cả tổ hợp. Dưới đây là một số lợi ích khi học về tổ hợp trên tic.edu.vn:

• Tài liệu đầy đủ và chi tiết: tic.edu.vn cung cấp các bài giảng, bài viết và bài tập về tổ hợp được biên soạn bởi các giáo viên và chuyên gia giàu kinh nghiệm. Các tài liệu này bao gồm đầy đủ các kiến thức cơ bản và nâng cao, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
• Ví dụ minh họa đa dạng: Các tài liệu trên tic.edu.vn đi kèm với rất nhiều ví dụ minh họa, giúp bạn hiểu rõ hơn về các khái niệm và công thức tổ hợp. Các ví dụ này được lựa chọn cẩn thận để bao phủ các dạng bài tập thường gặp trong các kỳ thi.
• Công cụ hỗ trợ học tập hiệu quả: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn tự kiểm tra kiến thức và rèn luyện kỹ năng giải toán. Các công cụ này bao gồm các bài kiểm tra trắc nghiệm, các bài tập tự luận và các trò chơi tương tác.
• Cộng đồng học tập sôi nổi: tic.edu.vn có một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và các bài toán hay với các bạn học và các giáo viên.
• Cập nhật thông tin mới nhất: tic.edu.vn luôn cập nhật thông tin mới nhất về các xu hướng giáo dục, các phương pháp học tập tiên tiến và các nguồn tài liệu mới.

Để bắt đầu học về tổ hợp trên tic.edu.vn, bạn có thể truy cập trang web và tìm kiếm các tài liệu liên quan đến tổ hợp, chỉnh hợp và hoán vị. Bạn cũng có thể tham gia cộng đồng học tập để trao đổi kiến thức và kinh nghiệm với các bạn học khác.

7. Lời Khuyên Để Học Tốt Về Tổ Hợp

Để học tốt về tổ hợp, bạn nên:

• Nắm vững kiến thức cơ bản: Trước khi bắt đầu học các kiến thức nâng cao, hãy đảm bảo rằng bạn đã nắm vững các kiến thức cơ bản về tập hợp, hàm số, giai thừa và các phép toán số học.
• Làm nhiều bài tập: Cách tốt nhất để học tổ hợp là làm nhiều bài tập. Hãy bắt đầu với các bài tập đơn giản và dần dần chuyển sang các bài tập phức tạp hơn.
• Tìm hiểu các ứng dụng thực tế: Việc tìm hiểu các ứng dụng thực tế của tổ hợp sẽ giúp bạn hiểu rõ hơn về tầm quan trọng của nó và có động lực học tập hơn.
• Trao đổi kiến thức với người khác: Hãy trao đổi kiến thức và kinh nghiệm với các bạn học và các giáo viên. Điều này sẽ giúp bạn hiểu rõ hơn về các khái niệm và kỹ năng giải toán.
• Sử dụng các công cụ hỗ trợ học tập: Hãy sử dụng các công cụ hỗ trợ học tập trực tuyến để tự kiểm tra kiến thức và rèn luyện kỹ năng giải toán.

8. FAQ – Các Câu Hỏi Thường Gặp Về Tổ Hợp Chập K Của N

1. Tổ hợp chập k của n là gì?

   • Tổ hợp chập k của n là số cách chọn k phần tử từ n phần tử mà không quan tâm đến thứ tự.

2. Công thức tính tổ hợp chập k của n là gì?

   • Công thức là $C_n^k = frac{n!}{k!(n-k)!}$.

3. Sự khác biệt giữa tổ hợp, chỉnh hợp và hoán vị là gì?

   • Hoán vị quan tâm đến thứ tự của tất cả các phần tử, chỉnh hợp quan tâm đến thứ tự của k phần tử được chọn, còn tổ hợp không quan tâm đến thứ tự.

4. Công thức Pascal là gì và nó được sử dụng để làm gì?

   • Công thức Pascal là $Cn^k = C{n-1}^k + C_{n-1}^{k-1}$, được sử dụng để tính toán giá trị của tổ hợp dựa trên các giá trị tổ hợp nhỏ hơn.

5. Tổ hợp có ứng dụng gì trong thực tế?

   • Tổ hợp có ứng dụng trong xác suất thống kê, tin học, kinh tế, di truyền học, mật mã học và nhiều lĩnh vực khác.

6. Làm thế nào để học tốt về tổ hợp?

   • Nắm vững kiến thức cơ bản, làm nhiều bài tập, tìm hiểu các ứng dụng thực tế, trao đổi kiến thức với người khác và sử dụng các công cụ hỗ trợ học tập.

7. tic.edu.vn cung cấp những tài liệu gì về tổ hợp?

   • tic.edu.vn cung cấp các bài giảng, bài viết, bài tập, ví dụ minh họa và công cụ hỗ trợ học tập trực tuyến về tổ hợp.

8. Làm thế nào để tìm tài liệu về tổ hợp trên tic.edu.vn?

   • Truy cập trang web tic.edu.vn và tìm kiếm các tài liệu liên quan đến tổ hợp, chỉnh hợp và hoán vị.

9. Tôi có thể hỏi đáp các thắc mắc về tổ hợp ở đâu trên tic.edu.vn?

   • Bạn có thể tham gia cộng đồng học tập trên tic.edu.vn để trao đổi kiến thức và kinh nghiệm với các bạn học khác.

10. tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu khác về tổ hợp?

    • tic.edu.vn cung cấp tài liệu đầy đủ, chi tiết, ví dụ minh họa đa dạng, công cụ hỗ trợ học tập hiệu quả, cộng đồng học tập sôi nổi và luôn cập nhật thông tin mới nhất.

9. Khám Phá Kho Tài Liệu Tổ Hợp Chập K Của N Vô Tận Tại Tic.edu.vn Ngay Hôm Nay

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về tổ hợp chập k của n? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm? Hãy đến với tic.edu.vn!

tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt về tổ hợp chập k của n, cập nhật thông tin giáo dục mới nhất và chính xác, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, xây dựng cộng đồng học tập trực tuyến sôi nổi và giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng.

Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn

tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức!