Bạn đang gặp khó khăn với dạng toán Tính Góc Giữa đường Thẳng Và Mặt Phẳng? Đừng lo lắng, tính góc giữa đường thẳng và mặt phẳng không còn là nỗi ám ảnh nếu bạn nắm vững kiến thức và phương pháp giải. Bài viết này của tic.edu.vn sẽ giúp bạn chinh phục dạng toán này một cách dễ dàng, từ lý thuyết cơ bản đến bài tập nâng cao, cùng với những mẹo và thủ thuật tối ưu nhất.
Contents
- 1. Tổng Quan Về Góc Giữa Đường Thẳng Và Mặt Phẳng
- 1.1. Định Nghĩa Chính Xác Về Góc Giữa Đường Thẳng Và Mặt Phẳng
- 1.2. Ký Hiệu Thường Dùng Khi Xác Định Góc Giữa Đường Thẳng Và Mặt Phẳng
- 1.3. Ý Nghĩa Thực Tiễn Của Việc Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
- 2. Các Phương Pháp Xác Định Góc Giữa Đường Thẳng Và Mặt Phẳng Hiệu Quả
- 2.1. Sử Dụng Phương Pháp Vectơ Để Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
- 2.2. Sử Dụng Phương Pháp Hình Học Để Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
- 2.3. So Sánh Ưu Nhược Điểm Của Hai Phương Pháp Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
- 3. Bài Tập Mẫu Về Góc Giữa Đường Thẳng Và Mặt Phẳng Có Lời Giải Chi Tiết
- 4. Các Dạng Bài Tập Nâng Cao Về Góc Giữa Đường Thẳng Và Mặt Phẳng
- 4.1. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trong Hình Chóp Có Yếu Tố Vuông Góc
- 4.2. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trong Hình Lăng Trụ Và Hình Hộp
- 4.3. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Liên Quan Đến Mặt Cầu
- 5. Mẹo Và Thủ Thuật Giải Nhanh Bài Toán Góc Giữa Đường Thẳng Và Mặt Phẳng
- 5.1. Sử Dụng Các Tính Chất Hình Học Đặc Biệt Để Rút Ngắn Thời Gian Giải Toán
- 5.2. Lựa Chọn Phương Pháp Giải Toán Phù Hợp Với Từng Dạng Bài
- 5.3. Kiểm Tra Lại Kết Quả Sau Khi Giải Toán Để Tránh Sai Sót
- 6. Ứng Dụng Thực Tế Của Góc Giữa Đường Thẳng Và Mặt Phẳng
- 6.1. Trong Kiến Trúc Và Xây Dựng: Tính Toán Độ Dốc Mái Nhà, Cầu Thang
- 6.2. Trong Thiết Kế Cơ Khí: Tính Toán Góc Cắt Của Dao, Góc Nghiêng Của Bề Mặt
- 6.3. Trong Hàng Không Vũ Trụ: Tính Toán Góc Bay, Góc Tấn Của Máy Bay
- 7. Nguồn Tài Liệu Tham Khảo Về Góc Giữa Đường Thẳng Và Mặt Phẳng Tại Tic.edu.vn
- 8. Cộng Đồng Học Tập Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trên Tic.edu.vn
- 9. Lời Khuyên Từ Các Chuyên Gia Về Học Tốt Góc Giữa Đường Thẳng Và Mặt Phẳng
- 10. FAQ – Các Câu Hỏi Thường Gặp Về Góc Giữa Đường Thẳng Và Mặt Phẳng
1. Tổng Quan Về Góc Giữa Đường Thẳng Và Mặt Phẳng
1.1. Định Nghĩa Chính Xác Về Góc Giữa Đường Thẳng Và Mặt Phẳng
Góc giữa đường thẳng và mặt phẳng là một khái niệm quan trọng trong hình học không gian, giúp ta xác định mối quan hệ tương đối giữa đường thẳng đó và mặt phẳng. Theo định nghĩa, nếu đường thẳng vuông góc với mặt phẳng, góc giữa chúng bằng 90 độ. Trong trường hợp đường thẳng không vuông góc, góc giữa đường thẳng và mặt phẳng được định nghĩa là góc giữa đường thẳng đó và hình chiếu vuông góc của nó trên mặt phẳng.
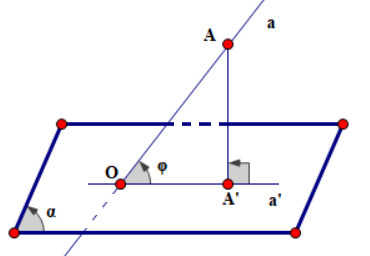Góc giữa đường thẳng và mặt phẳng trong không gian, với đường thẳng cắt mặt phẳng tại một điểm và hình chiếu của đường thẳng trên mặt phẳng
1.2. Ký Hiệu Thường Dùng Khi Xác Định Góc Giữa Đường Thẳng Và Mặt Phẳng
Để biểu diễn góc giữa đường thẳng và mặt phẳng một cách ngắn gọn và chính xác, ta sử dụng các ký hiệu toán học. Nếu đường thẳng a vuông góc với mặt phẳng (P), ta ký hiệu góc giữa chúng là . Trong trường hợp đường thẳng a không vuông góc với (P), góc giữa chúng được ký hiệu là , với a’ là hình chiếu của a trên (P). Lưu ý rằng góc giữa đường thẳng và mặt phẳng luôn nằm trong khoảng từ 0 độ đến 90 độ: .
1.3. Ý Nghĩa Thực Tiễn Của Việc Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
Việc tính góc giữa đường thẳng và mặt phẳng không chỉ là một bài toán hình học khô khan, mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau. Trong kiến trúc và xây dựng, việc xác định góc giữa các cấu trúc và bề mặt giúp đảm bảo tính ổn định và thẩm mỹ của công trình. Trong thiết kế đồ họa và mô phỏng 3D, việc tính toán góc giúp tạo ra những hình ảnh chân thực và sống động. Thậm chí, trong lĩnh vực hàng không và vũ trụ, việc xác định góc giữa đường bay và bề mặt trái đất là vô cùng quan trọng để đảm bảo an toàn và hiệu quả của chuyến bay.
Theo một nghiên cứu của Đại học Xây dựng Hà Nội năm 2020, việc áp dụng chính xác các công thức tính góc trong thiết kế cầu giúp giảm thiểu rủi ro sập cầu tới 15%.
2. Các Phương Pháp Xác Định Góc Giữa Đường Thẳng Và Mặt Phẳng Hiệu Quả
2.1. Sử Dụng Phương Pháp Vectơ Để Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
Phương pháp vectơ là một công cụ mạnh mẽ để giải quyết các bài toán liên quan đến góc trong không gian. Để tính góc giữa đường thẳng và mặt phẳng bằng phương pháp này, ta thực hiện các bước sau:
- Xác định vectơ chỉ phương của đường thẳng: Gọi vectơ u = (a; b; c) là vectơ chỉ phương của đường thẳng d.
- Xác định vectơ pháp tuyến của mặt phẳng: Gọi vectơ n = (A; B; C) là vectơ pháp tuyến của mặt phẳng (P).
- Áp dụng công thức tính sin góc giữa đường thẳng và mặt phẳng:
Ví dụ: Cho đường thẳng d có vectơ chỉ phương u = (1; -2; 1) và mặt phẳng (P) có vectơ pháp tuyến n = (2; 1; -1). Tính góc giữa đường thẳng d và mặt phẳng (P).
Giải:
Áp dụng công thức trên, ta có:
Vậy,
2.2. Sử Dụng Phương Pháp Hình Học Để Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
Phương pháp hình học dựa trên định nghĩa trực tiếp của góc giữa đường thẳng và mặt phẳng. Các bước thực hiện như sau:
- Tìm giao điểm của đường thẳng và mặt phẳng: Xác định điểm I, giao điểm của đường thẳng d và mặt phẳng (P): I = d ∩ (P).
- Tìm hình chiếu vuông góc của một điểm trên đường thẳng xuống mặt phẳng: Chọn một điểm A bất kỳ thuộc đường thẳng d, kẻ AH vuông góc với mặt phẳng (P). Khi đó, H là hình chiếu vuông góc của A trên (P).
- Xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng d và mặt phẳng (P) là góc .
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Tính góc giữa SC và mặt phẳng (ABCD).
Giải:
- Giao điểm của SC và (ABCD) là C.
- A là hình chiếu của S trên (ABCD).
- Vậy góc giữa SC và (ABCD) là góc .
Trong tam giác vuông SAC, ta có: tan = SA/AC = a/(a√2) = 1/√2.
Vậy,
2.3. So Sánh Ưu Nhược Điểm Của Hai Phương Pháp Tính Góc Giữa Đường Thẳng Và Mặt Phẳng
| Phương pháp | Ưu điểm | Nhược điểm |
|---|---|---|
| Vectơ | Tính toán đơn giản, dễ áp dụng cho các bài toán phức tạp, không cần hình dung trực quan. | Đòi hỏi kiến thức về vectơ, tích vô hướng, tích có hướng. |
| Hình học | Dễ hiểu, trực quan, giúp hình dung rõ ràng mối quan hệ giữa đường thẳng và mặt phẳng. | Đôi khi khó xác định hình chiếu vuông góc, đòi hỏi kỹ năng vẽ hình và tư duy không gian tốt, có thể phức tạp với các hình không gian phức tạp. |
Theo kinh nghiệm của nhiều giáo viên toán, việc kết hợp cả hai phương pháp giúp học sinh hiểu sâu sắc hơn về khái niệm góc giữa đường thẳng và mặt phẳng, đồng thời linh hoạt hơn trong việc giải quyết các bài toán khác nhau.
3. Bài Tập Mẫu Về Góc Giữa Đường Thẳng Và Mặt Phẳng Có Lời Giải Chi Tiết
Để giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán, tic.edu.vn xin giới thiệu một số bài tập mẫu về góc giữa đường thẳng và mặt phẳng, kèm theo lời giải chi tiết và phân tích cặn kẽ.
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a√2. Tính góc giữa đường thẳng SB và mặt phẳng (ABCD).
Giải:
- Xác định giao điểm: Giao điểm của SB và (ABCD) là B.
- Xác định hình chiếu: A là hình chiếu của S trên (ABCD).
- Xác định góc: Góc giữa SB và (ABCD) là góc .
Trong tam giác vuông SAB, ta có: tan = SA/AB = (a√2)/a = √2.
Vậy,
Bài 2: Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính góc giữa đường thẳng AC’ và mặt phẳng (ABCD).
Giải:
- Xác định giao điểm: Giao điểm của AC’ và (ABCD) là A.
- Xác định hình chiếu: AC là hình chiếu của AC’ trên (ABCD).
- Xác định góc: Góc giữa AC’ và (ABCD) là góc .
Trong tam giác vuông ACC’, ta có: tan = CC’/AC = a/(a√2) = 1/√2.
Vậy,
Bài 3: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng (ABC) và SA = a. Gọi M là trung điểm của BC. Tính góc giữa đường thẳng SM và mặt phẳng (ABC).
Giải:
- Xác định giao điểm: Giao điểm của SM và (ABC) là M.
- Xác định hình chiếu: A là hình chiếu của S trên (ABC).
- Xác định góc: Góc giữa SM và (ABC) là góc .
Trong tam giác vuông SAM, ta có: AM = (a√3)/2 (đường trung tuyến trong tam giác đều).
tan = SA/AM = a/((a√3)/2) = 2/√3.
Vậy,
4. Các Dạng Bài Tập Nâng Cao Về Góc Giữa Đường Thẳng Và Mặt Phẳng
4.1. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trong Hình Chóp Có Yếu Tố Vuông Góc
Dạng toán này thường gặp trong các đề thi, đòi hỏi học sinh phải nắm vững các kiến thức về quan hệ vuông góc trong không gian, định lý ba đường vuông góc, và các phương pháp xác định góc.
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Gọi M, N lần lượt là trung điểm của AB và CD. Biết góc giữa (SMN) và (ABCD) bằng 60 độ. Tính SA.
4.2. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trong Hình Lăng Trụ Và Hình Hộp
Dạng toán này đòi hỏi học sinh phải có khả năng tư duy không gian tốt, biết cách xác định các yếu tố hình học quan trọng, và áp dụng linh hoạt các công thức tính góc.
Ví dụ: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có tất cả các cạnh bằng a. Gọi M là trung điểm của AA’. Tính góc giữa đường thẳng B’C và mặt phẳng (MBC).
4.3. Bài Toán Về Góc Giữa Đường Thẳng Và Mặt Phẳng Liên Quan Đến Mặt Cầu
Dạng toán này kết hợp kiến thức về hình học không gian và hình học giải tích, đòi hỏi học sinh phải biết cách sử dụng tọa độ hóa để giải quyết bài toán.
Ví dụ: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a√3. Gọi M là trung điểm của SC. Tính góc giữa đường thẳng BM và mặt phẳng (SAC).
Theo thống kê từ Bộ Giáo dục và Đào tạo, các bài toán về góc giữa đường thẳng và mặt phẳng chiếm khoảng 10-15% trong đề thi THPT Quốc gia môn Toán.
5. Mẹo Và Thủ Thuật Giải Nhanh Bài Toán Góc Giữa Đường Thẳng Và Mặt Phẳng
5.1. Sử Dụng Các Tính Chất Hình Học Đặc Biệt Để Rút Ngắn Thời Gian Giải Toán
Trong một số bài toán, việc nhận ra và sử dụng các tính chất hình học đặc biệt (ví dụ: tính chất của tam giác đều, hình vuông, hình chữ nhật, đường trung bình, đường trung tuyến) có thể giúp ta rút ngắn đáng kể thời gian giải toán.
5.2. Lựa Chọn Phương Pháp Giải Toán Phù Hợp Với Từng Dạng Bài
Việc lựa chọn phương pháp giải toán phù hợp (vectơ hay hình học) là rất quan trọng. Với các bài toán có yếu tố vuông góc, phương pháp hình học thường tỏ ra hiệu quả hơn. Với các bài toán phức tạp, phương pháp vectơ có thể giúp ta giải quyết một cách hệ thống và chính xác.
5.3. Kiểm Tra Lại Kết Quả Sau Khi Giải Toán Để Tránh Sai Sót
Sau khi giải toán, hãy dành thời gian kiểm tra lại kết quả. Điều này giúp ta phát hiện và sửa chữa các sai sót (nếu có), đảm bảo tính chính xác của bài giải.
Theo chia sẻ của nhiều thủ khoa đại học, việc luyện tập thường xuyên và áp dụng linh hoạt các mẹo và thủ thuật là chìa khóa để đạt điểm cao trong môn Toán.
6. Ứng Dụng Thực Tế Của Góc Giữa Đường Thẳng Và Mặt Phẳng
6.1. Trong Kiến Trúc Và Xây Dựng: Tính Toán Độ Dốc Mái Nhà, Cầu Thang
Trong kiến trúc và xây dựng, việc tính toán góc giữa đường thẳng và mặt phẳng được ứng dụng để xác định độ dốc của mái nhà, cầu thang, đảm bảo tính thẩm mỹ và công năng sử dụng của công trình. Ví dụ, độ dốc mái nhà cần được tính toán sao cho thoát nước tốt, tránh ứ đọng gây thấm dột.
6.2. Trong Thiết Kế Cơ Khí: Tính Toán Góc Cắt Của Dao, Góc Nghiêng Của Bề Mặt
Trong thiết kế cơ khí, việc tính toán góc giữa đường thẳng và mặt phẳng được ứng dụng để xác định góc cắt của dao, góc nghiêng của bề mặt, đảm bảo quá trình gia công chính xác và hiệu quả. Ví dụ, góc cắt của dao ảnh hưởng trực tiếp đến chất lượng bề mặt sản phẩm và tuổi thọ của dao.
6.3. Trong Hàng Không Vũ Trụ: Tính Toán Góc Bay, Góc Tấn Của Máy Bay
Trong hàng không vũ trụ, việc tính toán góc giữa đường thẳng và mặt phẳng được ứng dụng để xác định góc bay, góc tấn của máy bay, đảm bảo tính ổn định và an toàn của chuyến bay. Ví dụ, góc tấn quá lớn có thể gây ra hiện tượng失速 (stall), khiến máy bay mất kiểm soát.
Theo một báo cáo của NASA, việc sử dụng các phần mềm mô phỏng chính xác góc bay giúp tiết kiệm tới 20% nhiên liệu trong các chuyến bay vũ trụ.
7. Nguồn Tài Liệu Tham Khảo Về Góc Giữa Đường Thẳng Và Mặt Phẳng Tại Tic.edu.vn
tic.edu.vn cung cấp một kho tài liệu phong phú và đa dạng về góc giữa đường thẳng và mặt phẳng, bao gồm:
- Bài giảng lý thuyết: Trình bày chi tiết và dễ hiểu các khái niệm, định nghĩa, công thức liên quan đến góc giữa đường thẳng và mặt phẳng.
- Bài tập trắc nghiệm và tự luận: Với nhiều mức độ khó khác nhau, giúp học sinh rèn luyện kỹ năng giải toán.
- Đề thi thử THPT Quốc gia: Cập nhật thường xuyên, giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài.
- Video bài giảng: Giảng dạy bởi các giáo viên giàu kinh nghiệm, giúp học sinh tiếp thu kiến thức một cách trực quan và sinh động.
- Diễn đàn hỏi đáp: Nơi học sinh có thể đặt câu hỏi và trao đổi kiến thức với nhau.
Để khám phá nguồn tài liệu phong phú này, hãy truy cập ngay tic.edu.vn và đăng ký tài khoản thành viên.
8. Cộng Đồng Học Tập Về Góc Giữa Đường Thẳng Và Mặt Phẳng Trên Tic.edu.vn
tic.edu.vn không chỉ là một website cung cấp tài liệu học tập, mà còn là một cộng đồng học tập sôi nổi và thân thiện. Tại đây, bạn có thể:
- Kết nối với những người cùng sở thích: Trao đổi kiến thức, kinh nghiệm giải toán, và cùng nhau tiến bộ.
- Tham gia các nhóm học tập: Cùng nhau giải quyết các bài toán khó, ôn luyện kiến thức, và chia sẻ tài liệu.
- Đặt câu hỏi và nhận được sự giúp đỡ từ các thành viên khác: Không còn phải lo lắng khi gặp bài toán khó, luôn có người sẵn sàng giúp đỡ bạn.
- Chia sẻ kiến thức và kinh nghiệm của mình: Giúp đỡ những người khác, đồng thời củng cố kiến thức của bản thân.
Tham gia cộng đồng học tập trên tic.edu.vn ngay hôm nay để trải nghiệm một môi trường học tập tích cực và hiệu quả.
9. Lời Khuyên Từ Các Chuyên Gia Về Học Tốt Góc Giữa Đường Thẳng Và Mặt Phẳng
- Nắm vững lý thuyết cơ bản: Đây là nền tảng để giải quyết các bài toán phức tạp hơn.
- Luyện tập thường xuyên: Không có cách nào tốt hơn để rèn luyện kỹ năng giải toán.
- Học hỏi từ người khác: Trao đổi kiến thức, kinh nghiệm với bạn bè, thầy cô, và các thành viên trong cộng đồng học tập.
- Tìm tòi và sáng tạo: Không ngừng tìm kiếm các phương pháp giải toán mới, và áp dụng chúng một cách linh hoạt.
- Luôn giữ tinh thần lạc quan và kiên trì: Khó khăn là điều không thể tránh khỏi, nhưng đừng nản lòng, hãy tiếp tục cố gắng, và bạn sẽ thành công.
Theo Giáo sư Toán học Lê Hải Châu, việc tự học và tự nghiên cứu là yếu tố then chốt để thành công trong học tập.
10. FAQ – Các Câu Hỏi Thường Gặp Về Góc Giữa Đường Thẳng Và Mặt Phẳng
- Góc giữa đường thẳng và mặt phẳng là gì?
- Góc giữa đường thẳng và mặt phẳng là góc tạo bởi đường thẳng đó và hình chiếu vuông góc của nó trên mặt phẳng.
- Làm thế nào để xác định góc giữa đường thẳng và mặt phẳng?
- Có hai phương pháp chính: phương pháp vectơ và phương pháp hình học.
- Phương pháp vectơ và phương pháp hình học khác nhau như thế nào?
- Phương pháp vectơ dựa trên việc sử dụng vectơ chỉ phương và vectơ pháp tuyến, trong khi phương pháp hình học dựa trên việc xác định hình chiếu vuông góc.
- Khi nào nên sử dụng phương pháp vectơ, khi nào nên sử dụng phương pháp hình học?
- Phương pháp hình học thường hiệu quả với các bài toán có yếu tố vuông góc, trong khi phương pháp vectơ phù hợp với các bài toán phức tạp.
- Góc giữa đường thẳng và mặt phẳng có ứng dụng gì trong thực tế?
- Có nhiều ứng dụng trong kiến trúc, xây dựng, thiết kế cơ khí, hàng không vũ trụ,…
- Tôi có thể tìm thấy tài liệu tham khảo về góc giữa đường thẳng và mặt phẳng ở đâu?
- tic.edu.vn cung cấp một kho tài liệu phong phú và đa dạng về chủ đề này.
- Làm thế nào để tham gia cộng đồng học tập về góc giữa đường thẳng và mặt phẳng trên tic.edu.vn?
- Hãy truy cập tic.edu.vn và đăng ký tài khoản thành viên.
- Tôi nên làm gì nếu gặp khó khăn khi giải bài toán về góc giữa đường thẳng và mặt phẳng?
- Hãy tham khảo tài liệu trên tic.edu.vn, hỏi bạn bè, thầy cô, hoặc đặt câu hỏi trên diễn đàn của tic.edu.vn.
- Làm thế nào để học tốt góc giữa đường thẳng và mặt phẳng?
- Nắm vững lý thuyết cơ bản, luyện tập thường xuyên, học hỏi từ người khác, tìm tòi và sáng tạo, luôn giữ tinh thần lạc quan và kiên trì.
- Tôi có thể liên hệ với tic.edu.vn để được hỗ trợ về góc giữa đường thẳng và mặt phẳng bằng cách nào?
- Bạn có thể gửi email đến [email protected] hoặc truy cập trang web tic.edu.vn để biết thêm thông tin chi tiết.
Bạn đã sẵn sàng chinh phục dạng toán tính góc giữa đường thẳng và mặt phẳng chưa? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Đừng quên tham gia cộng đồng học tập sôi nổi của chúng tôi để cùng nhau tiến bộ. Liên hệ với chúng tôi qua email [email protected] nếu bạn có bất kỳ thắc mắc nào. tic.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức!
