Khám Phá Công Thức Tính Diện Tích Tam Giác Đầy Đủ Nhất

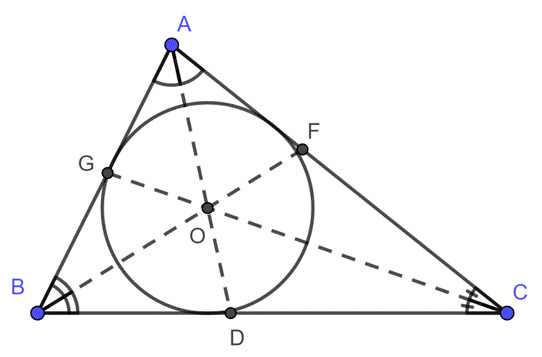
Diện tích tam giác là một khái niệm toán học quan trọng, được ứng dụng rộng rãi trong nhiều lĩnh vực. Bài viết này của tic.edu.vn sẽ cung cấp cho bạn cái nhìn toàn diện về các phương pháp Tính Diện Tích Tam Giác, từ cơ bản đến nâng cao, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán. Hãy cùng tic.edu.vn khám phá thế giới hình học và chinh phục những công thức tính diện tích tam giác thú vị nhé!

1. Tam Giác Là Gì? Tổng Quan Về Tam Giác Cần Nắm Vững

Trước khi đi sâu vào các công thức tính diện tích, việc hiểu rõ về tam giác và các yếu tố liên quan là vô cùng quan trọng.

1.1. Định Nghĩa Hình Tam Giác

Hình tam giác là một đa giác có ba cạnh và ba góc. Đây là một trong những hình học cơ bản nhất, đóng vai trò quan trọng trong nhiều lĩnh vực của toán học và ứng dụng thực tế.

Hình tam giác là một hình đa giác ba cạnh, nền tảng của nhiều khái niệm hình học.

1.2. Phân Loại Tam Giác Theo Cạnh và Góc

Tam giác có thể được phân loại dựa trên độ dài các cạnh và số đo các góc. Việc phân loại này giúp chúng ta chọn công thức tính diện tích phù hợp nhất.

1.2.1. Phân Loại Theo Cạnh:

• Tam giác đều: Ba cạnh bằng nhau, ba góc bằng 60 độ.
• Tam giác cân: Ít nhất hai cạnh bằng nhau.
• Tam giác thường: Ba cạnh có độ dài khác nhau.

1.2.2. Phân Loại Theo Góc:

• Tam giác nhọn: Ba góc đều nhỏ hơn 90 độ.
• Tam giác tù: Một góc lớn hơn 90 độ.
• Tam giác vuông: Một góc bằng 90 độ.

1.3. Các Tính Chất Quan Trọng Của Tam Giác

Hiểu rõ các tính chất của tam giác giúp bạn giải quyết bài tập hiệu quả hơn.

1. Tổng ba góc trong một tam giác luôn bằng 180 độ. Đây là một định lý cơ bản, được sử dụng rộng rãi trong các bài toán hình học.
2. Bất đẳng thức tam giác: Tổng độ dài hai cạnh bất kỳ luôn lớn hơn độ dài cạnh còn lại.
3. Định lý Pythagoras: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.
4. Đường trung tuyến: Đường thẳng nối đỉnh của tam giác với trung điểm cạnh đối diện. Ba đường trung tuyến cắt nhau tại trọng tâm của tam giác.
5. Đường phân giác: Đường thẳng chia một góc của tam giác thành hai góc bằng nhau.
6. Đường cao: Đường thẳng vuông góc với một cạnh của tam giác, kẻ từ đỉnh đối diện.

2. Tổng Hợp 7 Công Thức Tính Diện Tích Tam Giác Chi Tiết và Dễ Hiểu

Để tính diện tích tam giác, chúng ta có nhiều công thức khác nhau, tùy thuộc vào thông tin đã biết về tam giác đó. Dưới đây là tổng hợp 7 công thức quan trọng nhất:

Có nhiều công thức khác nhau để tính diện tích tam giác, tùy thuộc vào thông tin bạn có.

2.1. Diện Tích Tam Giác Thường Khi Biết Cạnh Đáy và Chiều Cao

Đây là công thức cơ bản nhất để tính diện tích tam giác.

• Công thức: S = 1/2 a h
  • Trong đó:
    • S là diện tích tam giác.
    • a là độ dài cạnh đáy.
    • h là chiều cao tương ứng với cạnh đáy a.

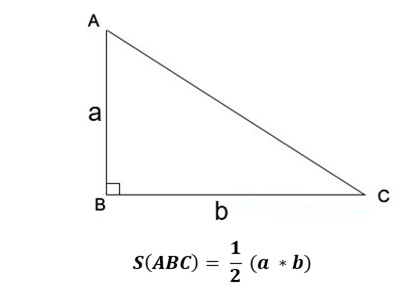
2.2. Diện Tích Tam Giác Vuông

Tam giác vuông có một góc bằng 90 độ. Công thức tính diện tích tam giác vuông đơn giản hơn so với tam giác thường.

• Công thức: S = 1/2 a b
  • Trong đó:
    • a và b là độ dài hai cạnh góc vuông.

Công thức đơn giản giúp tính diện tích tam giác vuông một cách nhanh chóng.

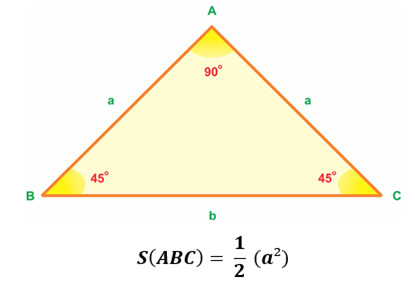
2.3. Diện Tích Tam Giác Vuông Cân

Tam giác vuông cân là tam giác vừa vuông, vừa cân. Hai cạnh góc vuông của tam giác này bằng nhau.

• Công thức: S = 1/2 * a^2
  • Trong đó:
    • a là độ dài cạnh góc vuông.

Diện tích tam giác vuông cân được tính bằng một nửa bình phương cạnh góc vuông.

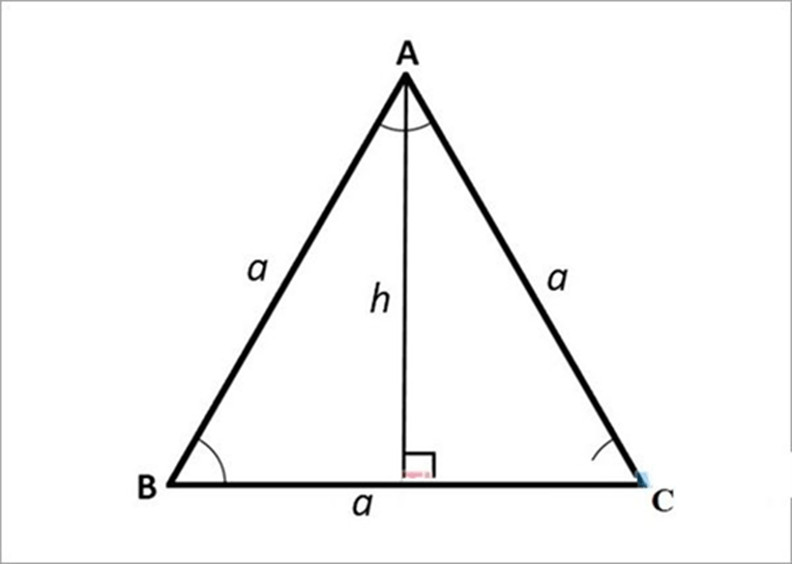
2.4. Diện Tích Tam Giác Cân

Tam giác cân có hai cạnh bằng nhau. Để tính diện tích tam giác cân, ta cần biết độ dài cạnh đáy và chiều cao tương ứng.

• Công thức: S = 1/2 a h
  • Trong đó:
    • a là độ dài cạnh đáy (cạnh khác hai cạnh bên).
    • h là chiều cao hạ từ đỉnh đối diện xuống cạnh đáy.

2.5. Diện Tích Tam Giác Đều

Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng 60 độ.

• Công thức: S = (a^2 * √3) / 4
  • Trong đó:
    • a là độ dài cạnh của tam giác đều.

Công thức này giúp tính diện tích tam giác đều một cách dễ dàng.

2.6. Công Thức Heron – Tính Diện Tích Khi Biết Ba Cạnh

Công thức Heron cho phép tính diện tích tam giác khi biết độ dài ba cạnh mà không cần chiều cao.

• Công thức: S = √(p (p – a) (p – b) * (p – c))
  • Trong đó:
    • a, b, c là độ dài ba cạnh của tam giác.
    • p là nửa chu vi của tam giác: p = (a + b + c) / 2.

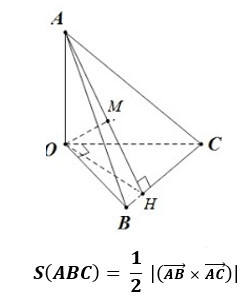
2.7. Diện Tích Tam Giác Trong Hệ Tọa Độ Oxyz

Trong không gian ba chiều, diện tích tam giác có thể được tính bằng công thức sử dụng tích có hướng của hai vectơ.

• Công thức: S = 1/2 * |[AB, AC]|
  • Trong đó:
    • A(x1, y1, z1), B(x2, y2, z2), C(x3, y3, z3) là tọa độ ba đỉnh của tam giác.
    • AB = (x2 – x1, y2 – y1, z2 – z1) và AC = (x3 – x1, y3 – y1, z3 – z1) là hai vectơ tạo bởi ba đỉnh.
    • [AB, AC] là tích có hướng của hai vectơ AB và AC.
    • |[AB, AC]| là độ dài của vectơ tích có hướng.

Công thức này hữu ích khi làm việc với hình học không gian.

3. Các Dạng Bài Tập Tính Diện Tích Tam Giác Thường Gặp

Việc luyện tập các dạng bài tập khác nhau giúp bạn nắm vững kiến thức và áp dụng linh hoạt các công thức.

3.1. Bài Tập Khi Biết Chiều Dài Cạnh Đáy và Chiều Cao

Đây là dạng bài tập cơ bản nhất, yêu cầu bạn áp dụng trực tiếp công thức S = 1/2 a h.

• Ví dụ: Tam giác ABC có cạnh đáy BC = 10cm và chiều cao AH = 5cm. Tính diện tích tam giác ABC.
  • Giải: S = 1/2 10cm 5cm = 25cm².

3.2. Bài Tập Khi Biết Độ Dài Ba Cạnh

Trong trường hợp này, bạn cần sử dụng công thức Heron để tính diện tích.

• Ví dụ: Tam giác ABC có AB = 3cm, BC = 4cm, CA = 5cm. Tính diện tích tam giác ABC.
  • Giải:
    • p = (3 + 4 + 5) / 2 = 6cm.
    • S = √(6 (6 – 3) (6 – 4) (6 – 5)) = √(6 3 2 1) = √36 = 6cm².

3.3. Bài Tập Tính Diện Tích Tam Giác Đều Khi Biết Một Cạnh

Áp dụng công thức S = (a^2 * √3) / 4 để giải quyết dạng bài tập này.

• Ví dụ: Tam giác đều ABC có cạnh AB = 4cm. Tính diện tích tam giác ABC.
  • Giải: S = (4^2 √3) / 4 = (16 √3) / 4 = 4√3 cm².

3.4. Bài Tập Tính Diện Tích Tam Giác Trong Tọa Độ Oxyz

Sử dụng công thức S = 1/2 * |[AB, AC]| để giải.

• Ví dụ: Cho tam giác ABC có A(1, 1, 1), B(2, 3, 4), C(5, 6, 7). Tính diện tích tam giác ABC.
  • Giải:
    • AB = (1, 2, 3), AC = (4, 5, 6).
    • [AB, AC] = (-3, 6, -3).
    • |[AB, AC]| = √( (-3)^2 + 6^2 + (-3)^2 ) = √54 = 3√6.
    • S = 1/2 * 3√6 = (3√6) / 2.

3.5. Tìm Cạnh Huyền Tam Giác Vuông Khi Biết Diện Tích và Một Cạnh Góc Vuông

Sử dụng công thức diện tích tam giác vuông và định lý Pythagoras để giải.

• Ví dụ: Tam giác vuông ABC tại A có diện tích 20cm² và cạnh AB = 4cm. Tính cạnh huyền BC.
  • Giải:
    • S = 1/2 AB AC => AC = (2 S) / AB = (2 20) / 4 = 10cm.
    • BC = √(AB^2 + AC^2) = √(4^2 + 10^2) = √116 = 2√29 cm.

3.6. Tìm Diện Tích Tam Giác Khi Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp

Sử dụng công thức S = (P * r) / 2.

• Ví dụ: Tam giác ABC có chu vi 24cm và bán kính đường tròn nội tiếp 2cm. Tính diện tích tam giác ABC.
  • Giải: S = (24 * 2) / 2 = 24cm².

Bán kính đường tròn nội tiếp và chu vi có thể giúp tính diện tích tam giác.

4. Bài Tập Mẫu Tính Diện Tích Tam Giác Chi Tiết

Để giúp bạn hiểu rõ hơn về cách áp dụng các công thức, chúng ta sẽ cùng xem xét một số bài tập mẫu.

4.1. Bài Tập 1: Tính Diện Tích Tam Giác Vuông

Đề bài: Cho tam giác ABC vuông tại A, có chiều cao AH = 4cm và cạnh góc vuông AB = 6cm. Tính diện tích tam giác ABC.

Lời giải:

• Vì tam giác ABC vuông tại A, ta có thể sử dụng công thức: S = 1/2 AB AC.
• Tuy nhiên, ta chưa biết độ dài cạnh AC. Ta có thể sử dụng định lý Pythagoras để tìm AC: AC = √(BC^2 – AB^2).
• Để tìm BC, ta sử dụng hệ thức lượng trong tam giác vuông: 1/AH^2 = 1/AB^2 + 1/AC^2. Từ đó, ta tìm được AC = 8cm.
• Vậy, diện tích tam giác ABC là: S = 1/2 6cm 8cm = 24cm².

4.2. Bài Tập 2: Tính Diện Tích Tam Giác Khi Biết Ba Cạnh

Đề bài: Tam giác ABC có độ dài ba cạnh là: AB = 5cm, BC = 7cm, AC = 8cm. Tính diện tích của tam giác ABC.

Lời giải:

• Ta sử dụng công thức Heron: S = √(p (p – a) (p – b) * (p – c)).
• Tính nửa chu vi: p = (5 + 7 + 8) / 2 = 10cm.
• Diện tích tam giác ABC là: S = √(10 (10 – 5) (10 – 7) (10 – 8)) = √(10 5 3 2) = √300 = 10√3 cm².

4.3. Bài Tập 3: Tính Diện Tích Tam Giác Khi Biết Chu Vi và Bán Kính Đường Tròn Nội Tiếp

Đề bài: Tam giác ABC có chu vi P = 20cm và bán kính đường tròn nội tiếp r = 3cm. Tính diện tích của tam giác ABC.

Lời giải:

• Ta sử dụng công thức: S = (P * r) / 2.
• Diện tích tam giác ABC là: S = (20cm * 3cm) / 2 = 30cm².

5. Các Câu Hỏi Thường Gặp Về Diện Tích Tam Giác

Dưới đây là một số câu hỏi thường gặp liên quan đến việc tính diện tích tam giác.

5.1. Cách Tính Diện Tích Tam Giác Lớp 5?

Ở lớp 5, học sinh thường được làm quen với công thức tính diện tích tam giác cơ bản: S = 1/2 a h, trong đó a là cạnh đáy và h là chiều cao tương ứng.

5.2. Làm Sao Để Tính Diện Tích Tam Giác Khi Biết 3 Cạnh?

Khi biết độ dài ba cạnh của tam giác, bạn có thể sử dụng công thức Heron: S = √(p (p – a) (p – b) * (p – c)), với p là nửa chu vi của tam giác.

5.3. Có Những Cách Tính Diện Tích Tam Giác Nào?

Có nhiều cách tính diện tích tam giác, tùy thuộc vào thông tin đã biết:

• Biết cạnh đáy và chiều cao: S = 1/2 a h.
• Biết hai cạnh góc vuông của tam giác vuông: S = 1/2 a b.
• Biết ba cạnh: Sử dụng công thức Heron.
• Biết tọa độ ba đỉnh trong không gian Oxyz: S = 1/2 * |[AB, AC]|.

6. Tại Sao Nên Chọn Tic.edu.vn Để Học Về Toán Học?

tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu học tập phong phú và chất lượng cao cho học sinh, sinh viên và những người yêu thích toán học.

• Đa dạng tài liệu: tic.edu.vn cung cấp đầy đủ các công thức, định lý, bài tập và lời giải chi tiết về diện tích tam giác, giúp bạn nắm vững kiến thức một cách toàn diện.
• Cập nhật liên tục: Các tài liệu trên tic.edu.vn luôn được cập nhật mới nhất, đảm bảo bạn tiếp cận được những thông tin chính xác và hữu ích nhất.
• Giao diện thân thiện: Giao diện của tic.edu.vn được thiết kế đơn giản, dễ sử dụng, giúp bạn dễ dàng tìm kiếm và học tập.
• Cộng đồng hỗ trợ: tic.edu.vn có một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, đặt câu hỏi và nhận được sự giúp đỡ từ những người cùng đam mê.

Bạn gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Hãy đến với tic.edu.vn để khám phá nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ càng. Chúng tôi cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng một cộng đồng học tập sôi nổi, nơi bạn có thể tương tác và học hỏi lẫn nhau.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá kho tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả!

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn

Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về diện tích tam giác. Chúc bạn học tập tốt và đạt được nhiều thành công!