**Tính Chất Đường Trung Bình Của Tam Giác: Ứng Dụng và Bài Tập**

Tính Chất đường Trung Bình là một khái niệm toán học quan trọng, mở ra nhiều ứng dụng thú vị trong giải toán và thực tiễn; tic.edu.vn sẽ giúp bạn khám phá sâu hơn về định nghĩa, tính chất và các bài tập liên quan đến đường trung bình của tam giác. Với nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả, tic.edu.vn sẽ là người bạn đồng hành đáng tin cậy trên hành trình chinh phục kiến thức toán học của bạn, giúp bạn nắm vững kiến thức, tự tin chinh phục mọi bài toán và mở rộng cơ hội học tập và phát triển bản thân.

1. Đường Trung Bình Của Tam Giác Là Gì?

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. Nó có những tính chất đặc biệt giúp giải quyết nhiều bài toán hình học một cách dễ dàng.

1.1. Định Nghĩa Đường Trung Bình Của Tam Giác

Đường trung bình của tam giác là đoạn thẳng nối trung điểm của hai cạnh bất kỳ trong tam giác đó. Định nghĩa này nghe có vẻ đơn giản, nhưng nó lại là chìa khóa để mở ra nhiều bài toán thú vị và ứng dụng thực tế. Theo GS.TSKH. Nguyễn Hữu Việt Hưng, Đại học Quốc gia Hà Nội, việc nắm vững định nghĩa này là bước đầu tiên để hiểu sâu hơn về các tính chất và ứng dụng của đường trung bình.

Ví dụ: Cho tam giác ABC, M là trung điểm của AB và N là trung điểm của AC. Khi đó, đoạn thẳng MN là đường trung bình của tam giác ABC.

Alt: Hình ảnh minh họa đường trung bình MN trong tam giác ABC, với M và N là trung điểm của AB và AC tương ứng.

1.2. Đặc Điểm Nhận Dạng Đường Trung Bình Của Tam Giác

Để nhận biết một đoạn thẳng có phải là đường trung bình của tam giác hay không, bạn cần kiểm tra xem đoạn thẳng đó có nối trung điểm của hai cạnh tam giác hay không. Nếu có, thì đó chính là đường trung bình.

Ví dụ: Trong tam giác PQR, nếu D là trung điểm của PQ và E là trung điểm của PR, thì DE chắc chắn là đường trung bình của tam giác PQR.

1.3. Số Lượng Đường Trung Bình Trong Một Tam Giác

Một tam giác có ba cạnh, do đó có ba đường trung bình, mỗi đường trung bình tương ứng với một cặp cạnh của tam giác. Điều này tạo ra sự đa dạng trong việc áp dụng các tính chất của đường trung bình để giải quyết các bài toán khác nhau. Theo TS. Trần Nam Dũng, Đại học Khoa học Tự nhiên TP.HCM, việc khai thác hiệu quả ba đường trung bình trong một tam giác có thể giúp giải quyết các bài toán phức tạp một cách sáng tạo.

2. Tính Chất Đường Trung Bình Của Tam Giác Quan Trọng Như Thế Nào?

Đường trung bình của tam giác sở hữu hai tính chất vô cùng quan trọng: song song với cạnh thứ ba và bằng nửa cạnh đó. Hai tính chất này là công cụ đắc lực để giải các bài toán liên quan đến hình học phẳng.

2.1. Tính Chất Về Song Song

Đường trung bình của một tam giác luôn song song với cạnh thứ ba của tam giác đó. Đây là một trong những tính chất quan trọng nhất và được ứng dụng rộng rãi trong việc chứng minh các bài toán liên quan đến tính song song và vuông góc.

Ví dụ: Cho tam giác ABC, MN là đường trung bình ứng với cạnh BC. Khi đó, MN // BC.

2.2. Tính Chất Về Độ Dài

Độ dài của đường trung bình bằng một nửa độ dài cạnh thứ ba mà nó song song. Tính chất này giúp chúng ta dễ dàng tính toán và so sánh độ dài các đoạn thẳng trong tam giác. Theo PGS.TS. Lê Thị Thanh Nhàn, Đại học Sư phạm Hà Nội, việc kết hợp cả hai tính chất về song song và độ dài giúp giải quyết các bài toán hình học một cách hiệu quả và chính xác.

Ví dụ: Cho tam giác ABC, MN là đường trung bình ứng với cạnh BC. Nếu BC = 10cm, thì MN = 5cm.

Alt: Hình ảnh minh họa tính chất đường trung bình MN song song với cạnh BC và có độ dài bằng một nửa BC trong tam giác ABC.

Alt: Hình ảnh minh họa đường trung bình DE song song với cạnh AC và có độ dài bằng một nửa AC trong tam giác ABC.

2.3. Ứng Dụng Của Tính Chất Đường Trung Bình Trong Chứng Minh Hình Học

Tính chất đường trung bình được sử dụng rộng rãi trong việc chứng minh các bài toán hình học. Dưới đây là một số ứng dụng tiêu biểu:

• Chứng minh hai đường thẳng song song: Nếu một đoạn thẳng là đường trung bình của một tam giác, nó sẽ song song với cạnh thứ ba.
• Tính độ dài đoạn thẳng: Nếu biết độ dài cạnh thứ ba, ta có thể dễ dàng tính được độ dài đường trung bình và ngược lại.
• Chứng minh các điểm thẳng hàng: Sử dụng tính chất đường trung bình để chứng minh các đoạn thẳng song song hoặc bằng nhau, từ đó suy ra các điểm thẳng hàng.

3. Các Dạng Bài Tập Về Đường Trung Bình Của Tam Giác

Để nắm vững kiến thức về đường trung bình, việc luyện tập các dạng bài tập khác nhau là vô cùng quan trọng. Dưới đây là một số dạng bài tập thường gặp và cách giải chi tiết.

3.1. Dạng 1: Tính Độ Dài Đường Trung Bình

Cho tam giác ABC, biết độ dài cạnh BC. Tính độ dài đường trung bình MN của tam giác ABC ứng với cạnh BC.

Cách giải:

• Xác định MN là đường trung bình của tam giác ABC ứng với cạnh BC.
• Áp dụng tính chất: MN = 1/2 BC.
• Thay số và tính toán.

Ví dụ: Cho tam giác ABC có BC = 8cm, MN là đường trung bình ứng với cạnh BC. Tính MN.

Giải: MN = 1/2 BC = 1/2 * 8 = 4cm.

3.2. Dạng 2: Chứng Minh Đường Thẳng Là Đường Trung Bình

Cho tam giác ABC, M là trung điểm của AB, N là trung điểm của AC. Chứng minh MN là đường trung bình của tam giác ABC.

Cách giải:

• Xác định M và N là trung điểm của AB và AC.
• Sử dụng định nghĩa: Đường trung bình là đoạn thẳng nối trung điểm hai cạnh của tam giác.
• Kết luận MN là đường trung bình của tam giác ABC.

Ví dụ: Cho tam giác DEF, P là trung điểm của DE, Q là trung điểm của DF. Chứng minh PQ là đường trung bình của tam giác DEF.

Giải: Vì P là trung điểm của DE và Q là trung điểm của DF, theo định nghĩa, PQ là đường trung bình của tam giác DEF.

3.3. Dạng 3: Ứng Dụng Đường Trung Bình Để Chứng Minh Tính Song Song

Cho tam giác ABC, MN là đường trung bình ứng với cạnh BC. Chứng minh MN song song với BC.

Cách giải:

• Xác định MN là đường trung bình của tam giác ABC ứng với cạnh BC.
• Áp dụng tính chất: Đường trung bình song song với cạnh thứ ba.
• Kết luận MN song song với BC.

Ví dụ: Cho tam giác GHI, RS là đường trung bình ứng với cạnh HI. Chứng minh RS song song với HI.

Giải: Vì RS là đường trung bình của tam giác GHI ứng với cạnh HI, theo tính chất, RS song song với HI.

3.4. Dạng 4: Ứng Dụng Đường Trung Bình Để Giải Các Bài Toán Thực Tế

Một khu vườn hình tam giác có cạnh đáy dài 20m. Người ta muốn làm một lối đi song song với cạnh đáy và đi qua trung điểm của hai cạnh bên. Tính độ dài của lối đi đó.

Cách giải:

• Xác định lối đi là đường trung bình của tam giác.
• Áp dụng tính chất: Đường trung bình bằng nửa cạnh đáy.
• Tính độ dài lối đi: 1/2 * 20 = 10m.

Ví dụ: Một tấm vải hình tam giác có cạnh đáy dài 30cm. Người ta cắt một đường thẳng song song với cạnh đáy và đi qua trung điểm của hai cạnh bên. Tính độ dài đường cắt đó.

Giải: Đường cắt đó là đường trung bình của tam giác, vậy độ dài đường cắt là 1/2 * 30 = 15cm.

4. Bài Tập Về Đường Trung Bình Của Tam Giác (Toán 8) – Kèm Lời Giải Chi Tiết

Dưới đây là một số bài tập về đường trung bình của tam giác trong chương trình Toán 8, kèm theo lời giải chi tiết, giúp bạn ôn luyện và nắm vững kiến thức.

4.1. Bài Tập Sách Giáo Khoa (Kết Nối Tri Thức)

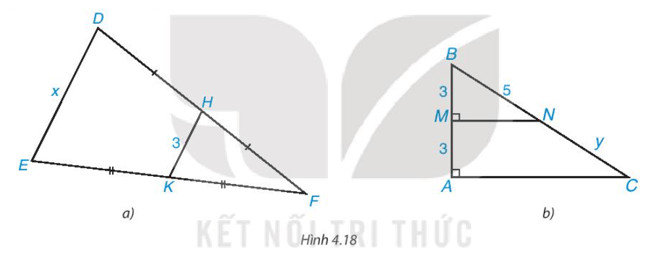
Bài 4.6 Trang 83 SGK Toán 8/1 Kết Nối Tri Thức

Alt: Hình ảnh bài 4.6 trang 83 SGK Toán 8/1 Kết Nối Tri Thức, yêu cầu tìm giá trị x và y dựa trên tính chất đường trung bình.

Giải:

• Hình 4.18a:

  • DH = HF, H ∈ DF nên H là trung điểm của DF.
  • EK = KF, K ∈ EF nên K là trung điểm của EF.
  • Xét tam giác DEF có H, K lần lượt là trung điểm của DF, EF nên HK là đường trung bình của tam giác DEF.

  => HK = 1/2 DE = 1/2 x

  Do đó x = 2HK = 2 . 3 = 6.

• Hình 4.18b:

  • Vì MN ⊥ AB, AC ⊥ AB nên MN // AC.
  • Mà M là trung điểm của AB (vì AM = BM = 3).
  • Suy ra MN là đường trung bình của tam giác ABC.

  Do đó N là trung điểm của BC nên y = NC = BN = 5.

Vậy x = 6; y = 5.

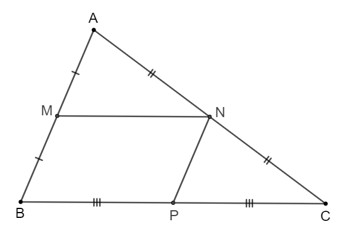
Bài 4.7 Trang 83 SGK Toán 8/1 Kết Nối Tri Thức

Alt: Hình ảnh bài 4.7 trang 83 SGK Toán 8/1 Kết Nối Tri Thức, yêu cầu chứng minh tứ giác BMNC là hình thang và tứ giác MNPB là hình bình hành.

Giải:

• a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của tam giác ABC suy ra MN // BC.

  Tứ giác BMNC có MN // BC nên tứ giác BMNC là hình thang (đpcm).

• b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của tam giác ABC suy ra NP // AB hay NP // MB.

  Tứ giác MNPB có MN // BP (do MN // BC); BM // NP (chứng minh trên).

Do đó, tứ giác MNPB là hình bình hành.

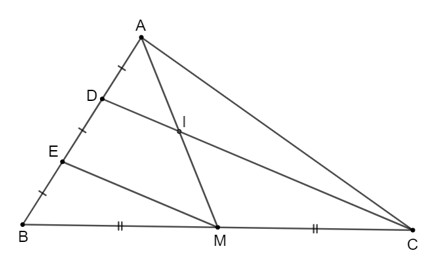
Bài 4.8 Trang 83 SGK Toán 8/1 Kết Nối Tri Thức

Alt: Hình ảnh bài 4.8 trang 83 SGK Toán 8/1 Kết Nối Tri Thức, yêu cầu chứng minh DC // EM và I là trung điểm của AM.

Giải:

• a) Vì AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.

  Ta có BE = DE và E ∈ BD nên E là trung điểm của BD.

  Xét tam giác BCD có E, M lần lượt là trung điểm của BD, BC nên EM là đường trung bình của tam giác BCD.

  Do đó DC // EM (tính chất đường trung bình).

• b) Ta có D là trung điểm của AE (vì AD = DE, D ∈ AE).

  Mà DI // EM (vì DC // EM).

Do đó DI là đường trung bình của tam giác AEM.

Suy ra I là trung điểm của AM.

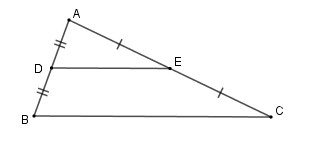
Bài 4.9 Trang 83 SGK Toán 8/1 Kết Nối Tri Thức

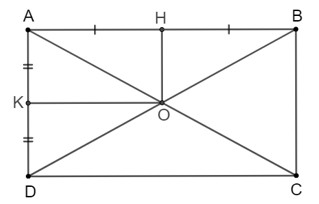
Alt: Hình ảnh bài 4.9 trang 83 SGK Toán 8/1 Kết Nối Tri Thức, yêu cầu chứng minh tứ giác AHOK là hình chữ nhật.

Giải:

Vì ABCD là hình chữ nhật nên ˆBAD = 90o và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường.

=> AB ⊥ AD; O là trung điểm của AC và BD.

Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của Δ ABD.

=> OH // AD mà AB ⊥ AD nên OH ⊥ AB hay ˆAHO = 90o

Tương tự, ta chứng minh được: OK ⊥ AD hay ˆAKO = 90o

Ta có ˆBAD+ˆAHO+ˆAKO+ˆHOK = 360o

=> ˆHOK = 360o – 90o – 90o – 90o = 90o

=> Tứ giác AHOK là hình chữ nhật.

4.2. Bài Tập Sách Giáo Khoa (Chân Trời Sáng Tạo)

Bài 1 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

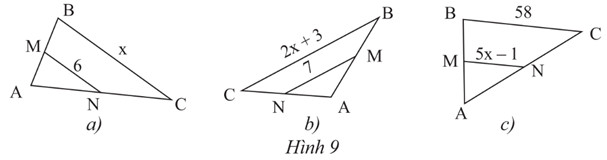
Alt: Hình ảnh bài 1 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu tính giá trị x dựa trên tính chất đường trung bình.

Giải:

• a) Xét tam giác ABC có MN là đường trung bình ta có:

  BC = 2MN => x = BC = 12.

• b) Xét tam giác ABC có MN là đường trung bình ta có:

  BC = 2MN => 2x + 3 = 14 => x = 5,5

• c) Xét tam giác ABC có MN là đường trung bình ta có:

  BC = 2MN => 58 = 2(5x − 1)

=> 58 = 10x – 2 => x = 6

Bài 2 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

Alt: Hình ảnh bài 2 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu tính độ dài PQ dựa trên tính chất đường trung bình.

Giải:

Xét tam giác ABC có:

AP = PB = 8 cm

AQ = QC = 7 cm

Khi đó, PQ là đường trung bình tam giác ABC.

Do đó PQ = 1/2 BC = 1/2 .9 = 4,5cm.

Bài 3 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

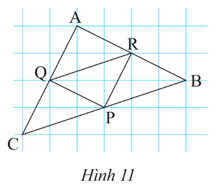
Alt: Hình ảnh bài 3 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu tính độ dài PQ, PR, RQ dựa trên tính chất đường trung bình.

Giải:

Ta có:

AB = √(2² + 4²) = 2√5

AC = √(2² + 4²) = 2√5

BC = √(2² + 6²) = 2√10

Xét Δ ABC có:

P là trung điểm của BC

Q lần lượt là trung điểm của AC

Do đó PQ là đường trung bình Δ ABC.

Khi đó:

PQ = 1/2 AB = 1/2 .2√5 = √5

Tương tự:

PR = 1/2 AC = 1/2 .2√5 = √5

RQ = 1/2 BC = 1/2 .2√10 = √10

Vậy PQ = √5; PR = √5; RQ = √10; AB = 2√5; AC = 2√5; BC = 2√10

Bài 4 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

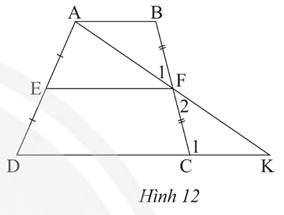
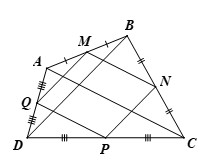
Alt: Hình ảnh bài 4 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu chứng minh các tính chất liên quan đến đường trung bình và tính song song.

Giải:

• a) Xét Δ FBA và FCK ta có:

  ˆF1 = ˆF2 (hai góc đối đỉnh)

  FB = FC (giả thiết)

  ˆFBA = ˆFCK (AB // CD, hai góc so le trong)

  Do đó Δ FBA = ΔFCK (g.c.g)

• b) Δ FBA = ΔFCK => FA = FK

  Xét Δ ADK có:

  EA = ED

  FA = FK

  => EF là đường trng bình tam giác ABC.

  => EF // DK

  Mà AB // CD nên EF // CD // AB.

• c) EF là đường trung bình Δ ADK.

  => EF = 1/2 DK = 1/2 (CD + CK)

  Mà CK = BA (do ΔFBA = ΔFCK) => EF = (AB+CD)/2

Bài 5 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

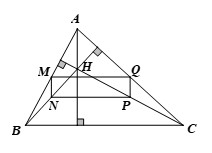
Alt: Hình ảnh bài 5 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu chứng minh tứ giác MNPH là hình thang cân.

Giải:

Xét Δ ABC ta có:

M là trung điểm của AB (gt);

N là trung điểm của AC (gt);

Do đó MN là đường trung bình của Δ ABC nên MN // BC.

=> tứ giác MNPH là hình thang.

Xét Δ ABC ta có:

M là trung điểm của AB (gt);

P là trung điểm của BC;

Do đó MP là đường trung bình của Δ ABC

=> MN = 1/2 AC

Vì Δ ACH vuông tại H có HN là trung tuyến (N là trung điểm của AC)

=> NH = 1/2 AC

Lại có MP = 1/2 AC => NH = MP

Hình thang MNPH (MN // PH) có MP = NH nên là hình thang cân.

Bài 6 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

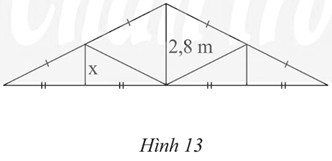
Alt: Hình ảnh bài 6 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu tính giá trị x dựa trên tính chất đường trung bình.

Giải:

Xét Δ ABH có:

AD = BD

BE = EH

Do đó DE là đường trung bình tam giác ABH

=> DE = 1/2 AH

=> x = 1/2 .2,8 = 1,4m

Bài 7 Trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo

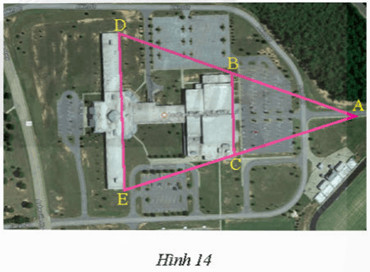
Alt: Hình ảnh bài 7 trang 54 SGK Toán 8/2 Chân Trời Sáng Tạo, yêu cầu tính độ dài DE dựa trên tính chất đường trung bình.

Giải:

Xét Δ ADE có:

B là trung điểm AD

C là trung điểm AE

Do đó BC là đường trung bình của Δ ADE.

Khi đó DE = 2BC = 2.232 = 464 (m).

4.3. Bài Tập Sách Giáo Khoa (Cánh Diều)

Bài 1 Trang 65 SGK Toán 8/1 Cánh Diều

Alt: Hình ảnh bài 1 trang 65 SGK Toán 8/1 Cánh Diều, yêu cầu chứng minh các tính chất liên quan đến đường trung bình và định lý Thalès.

Giải:

Xét Δ ABC với MN // BC, ta có: AM/MB = AN/NC (định lí Thalès)

Mà AM = MB (do M là trung điểm của AB) nên AN = NC.

Xét Δ ABC với MN // BC, ta có: AM/AB = MN/BC (hệ quả của định lí Thalès)

Mà AM = 1/2 AB (do M là trung điềm của AB)

=> MN = 1/2 BC

Bài 2 Trang 65 SGK Toán 8/1 Cánh Diều

Alt: Hình ảnh bài 2 trang 65 SGK Toán 8/1 Cánh Diều, yêu cầu chứng minh các tính chất liên quan đến đường trung bình và tính song song.

Giải:

• a) Do PN = NB nên N là trung điểm của BP.

  Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.

  Xét Δ BCP có M, N lần lượt là trung điểm của BC, BP nên MN là đường trung bình của ∆BCP

  => MN // CP.

• b) Do AP = PN nên P là trung điểm của AN.

  Mà MN // CP, Q ∈ CP nên MN // PQ.

  Xét Δ AMN có PQ đi qua P là trung điểm của AN và PQ // MN

  => Q là trung điểm của AM nên AQ = QM.

• c) Xét Δ AMN có P, Q lần lượt là trung điểm của AN, AM nên là đường trung bình của Δ AMN.

  => PQ = 1/2 MN

  Lại có MN là đường trung bình của ΔBCP

  => MN = 1/2 CP

Khi đó PQ = 1/2 MN = 1/2 .1/2 CP = 1/4 CP

=> CP = 4PQ.

Bài 3 Trang 65 SGK Toán 8/1 Cánh Diều

Alt: Hình ảnh bài 3 trang 65 SGK Toán 8/1 Cánh Diều, yêu cầu chứng minh các tính chất liên quan đến đường trung bình và hình bình hành, hình thoi, hình chữ nhật.

Giải:

• a) Xét Δ ABC có M, N lần lượt là trung điểm AB, BC nên MN là đường trung bình của ∆ABC

  => MN//AC và MN = 1/2 AC (1)

  Xét Δ ADC có P, Q lần lượt là trung điểm DC, AD nên PQ là đường trung bình của ΔADC

  => PQ//AC và PQ = 1/2 AC (2)

  Từ (1) và (2) => MN // PQ; MN = PQ.

  Tứ giác MNPQ có MN // PQ; MN = PQ nên MNPQ là hình bình hành.

• b) Xét Δ ABD có M, Q lần lượt là trung điểm AB, AD nên MQ là đường trung bình của Δ ABD

  => MQ // BD và MQ = 1/2 BD

  Mà MN = 1/2 AC và AC = BD nên MN = MQ.

  Hình bình hành MNPQ có MN = MQ nên MNPQ là hình thoi.

• c) Ta có MN // AC (câu a), MQ // BD (câu b) và AC ⊥ BD (giả thiết)

  Suy ra MN ⊥ MQ hay góc NMQ = 90o

Hình bình hành MNPQ có góc NMQ = 90o nên là hình chữ nhật.

Bài 4 Trang 65 SGK Toán 8/1 Cánh Diều

Alt: Hình ảnh bài 4 trang 65 SGK Toán 8/1 Cánh Diều, yêu cầu chứng minh tứ giác MNPQ là hình chữ nhật dựa trên tính chất đường trung bình.

Giải:

Xét ∆ABH có M, N lần lượt là trung điểm của AB, BH nên MN là đường trung bình Δ ABH.

Suy ra MN//AH (1)

Tương tự, xét ∆AHC ta cũng có PQ là đường trung bình Δ AHC nên PQ//AH (2)

Từ (1) và (2) ta có MN // PQ // AH.

Chứng minh tương tự như trên với Δ ABC và Δ HBC, ta cũng có MQ, NP lần lượt là đường trung bình của ΔABC và ΔHBC.

Do đó MQ // BC và NP // BC. Suy ra MQ // NP // BC.

Tứ giác MNPQ có MN // PQ và MQ // NP nên MNPQ là hình bình hành.

⦁ Ta có MN//AH và AH ⊥ BC (do H là trực tâm của ∆ABC) nên MN ⊥ BC

Lại có NP // BC nên => MN ⊥ NP hay góc MNP =90°.

Hình bình hành MNPQ có góc MNP =90° nên MNPQ là hình chữ nhật.

Bài 5 Trang 65 SGK Toán 8/1 Cánh Diều

Alt: Hình ảnh bài 5 trang 65 SGK Toán 8/1 Cánh Diều, yêu cầu tính khoảng cách giữa hai mép dưới của mái nhà dựa trên tính chất đường trung bình.

Giải:

Xét ∆ABC có MN là đường trung bình của ∆ABC nên MN=1/2BC

=> BC = 2MN = 2.4,5 = 9(m).

Vậy khoảng cách giữa hai mép dưới của mái khoảng 9 m.

5. Mở Rộng Kiến Thức Về Đường Trung Bình

Ngoài đường trung bình của tam giác, chúng ta còn có đường trung bình của hình thang. Vậy đường trung bình của hình thang có những tính chất gì đặc biệt?

5.1. Đường Trung Bình Của Hình Thang

Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. Tương tự như đường trung bình của tam giác, đường trung bình của hình thang cũng có những tính chất quan trọng.

Tính chất:

• Đường trung bình của hình thang song song với hai đáy.
• Đường trung bình của hình thang bằng nửa tổng độ dài hai đáy.

Ví dụ: Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Khi đó, MN là đường trung bình của hình thang ABCD và MN // AB // CD, MN = (AB + CD)/2.

5.2. Mối Liên Hệ Giữa Đường Trung Bình Của Tam Giác Và Hình Thang

Thực tế, đường trung bình của tam giác có thể coi là một trường hợp đặc biệt của đường trung bình hình thang, khi một trong hai đáy của hình thang bị thu выпадающий xuống thành một điểm.

6. Tại Sao Nên Học Toán Trên Tic.edu.vn?

Bạn đang tìm kiếm một nguồn tài liệu học tập toán đáng tin cậy và hiệu quả? Hãy đến với tic.edu.vn! Chúng tôi cung cấp:

• Tài liệu đa dạng và phong phú: Từ lý thuyết đến bài tập, từ cơ bản đến nâng cao, phù hợp với mọi trình độ học sinh.
• Cập nhật liên tục: Đảm bảo bạn luôn tiếp cận được những thông tin mới nhất và chính xác nhất.
• Công cụ hỗ trợ học tập hiệu quả: Giúp bạn ghi chú, quản lý thời gian và ôn tập kiến thức một cách khoa học.
• Cộng đồng học tập sôi nổi: Nơi bạn có thể trao đổi kiến thức, học hỏi kinh nghiệm và kết nối với những người cùng đam mê toán học.

Tic.edu.vn không chỉ là một website học tập, mà còn là một người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

7. Câu Hỏi Thường Gặp Về Đường Trung Bình Của Tam Giác

7.1. Đường trung bình của tam giác là gì?

Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

7.2. Một tam giác có bao nhiêu đường trung bình?

Một tam giác có ba đường trung bình, mỗi đường trung bình tương ứng với một cặp cạnh của tam giác.

7.3. Tính chất quan trọng nhất của đường trung bình là gì?

Đường trung bình song song với cạnh thứ ba và bằng nửa cạnh đó.

7.4. Làm thế nào để chứng minh một đoạn thẳng là đường trung bình của tam giác?

Chứng minh đoạn thẳng đó nối trung điểm của hai cạnh tam giác.

7.5. Đường trung bình có ứng dụng gì trong thực tế?

Đường trung bình được ứng dụng trong các bài toán đo đạc, thiết kế và xây dựng.

7.6. Đường trung bình của hình thang là gì?

Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

7.7. Tính chất của đường trung bình hình thang là gì?

Đường trung bình của hình thang song song với hai đáy và bằng nửa tổng độ dài hai đáy.

7.8. Làm thế nào để tìm tài liệu học tập về đường trung bình trên tic.edu.vn?

Bạn có thể tìm