**Tính Chất Hai Tiếp Tuyến Cắt Nhau: Ứng Dụng Và Bài Tập**

Tính chất hai tiếp tuyến cắt nhau là một kiến thức hình học quan trọng, khám phá ứng dụng thực tế và bài tập liên quan sẽ giúp bạn nắm vững kiến thức này. tic.edu.vn cung cấp tài liệu và công cụ hỗ trợ học tập, giúp bạn chinh phục kiến thức này một cách dễ dàng.

1. Định Nghĩa và Tính Chất Cơ Bản của Hai Tiếp Tuyến Cắt Nhau

1.1. Hai Tiếp Tuyến Cắt Nhau Là Gì?

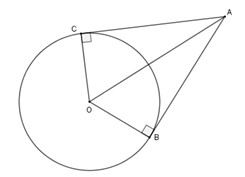
Hai tiếp tuyến cắt nhau là hai đường thẳng cùng tiếp xúc với một đường tròn tại hai điểm khác nhau và chúng giao nhau tại một điểm nằm ngoài đường tròn đó. Tính chất quan trọng của hai tiếp tuyến cắt nhau là nền tảng để giải quyết nhiều bài toán hình học.

1.2. Các Tính Chất Quan Trọng Cần Nắm Vững

Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm, thì điểm đó có những tính chất đặc biệt sau:

• Tính chất 1: Điểm đó cách đều hai tiếp điểm. Điều này có nghĩa là khoảng cách từ điểm giao nhau đến mỗi tiếp điểm là bằng nhau.
• Tính chất 2: Tia kẻ từ điểm đó đi qua tâm đường tròn là tia phân giác của góc tạo bởi hai tiếp tuyến.
• Tính chất 3: Tia kẻ từ tâm đường tròn đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc nắm vững các tính chất này cung cấp nền tảng vững chắc cho việc giải các bài toán liên quan đến tiếp tuyến của đường tròn.

Ví dụ, cho đường tròn (O), B và C là hai điểm nằm trên đường tròn đó. Giả sử tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A. Khi đó, ta có các kết quả sau:

• AB = AC (Điểm A cách đều hai tiếp điểm B và C)
• Tia OA là tia phân giác của góc BOC
• Tia AO là tia phân giác của góc BAC

2. Ứng Dụng Của Tính Chất Hai Tiếp Tuyến Cắt Nhau

2.1. Trong Chứng Minh Hình Học

Tính chất hai tiếp tuyến cắt nhau là công cụ hữu hiệu để chứng minh các bài toán liên quan đến tính song song, vuông góc và tính bằng nhau của các đoạn thẳng.

• Chứng minh các đoạn thẳng bằng nhau: Sử dụng tính chất điểm cắt nhau của hai tiếp tuyến cách đều hai tiếp điểm.
• Chứng minh các đường thẳng song song/vuông góc: Dựa vào tính chất tia phân giác của góc tạo bởi hai tiếp tuyến hoặc hai bán kính.

2.2. Trong Các Bài Toán Tính Toán

Tính chất này cũng giúp tính toán độ dài đoạn thẳng, số đo góc và các yếu tố khác trong hình học.

• Tính độ dài đoạn thẳng: Áp dụng tính chất hai tiếp tuyến cắt nhau để thiết lập các phương trình liên quan đến độ dài các đoạn thẳng.
• Tính số đo góc: Sử dụng tính chất tia phân giác để tìm ra mối liên hệ giữa các góc, từ đó tính toán số đo.

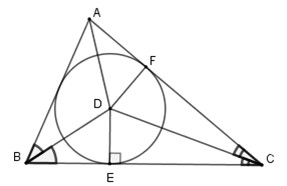
2.3. Đường Tròn Nội Tiếp và Bàng Tiếp Tam Giác

2.3.1. Đường Tròn Nội Tiếp Tam Giác

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác đó. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.

Theo nghiên cứu của Viện Nghiên cứu Sư phạm Quốc gia, việc hiểu rõ về đường tròn nội tiếp giúp học sinh phát triển tư duy hình học một cách toàn diện.

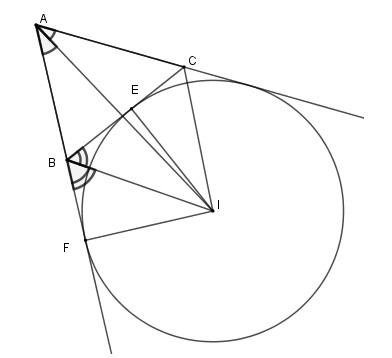
2.3.2. Đường Tròn Bàng Tiếp Tam Giác

Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh còn lại. Mỗi tam giác có ba đường tròn bàng tiếp. Tâm của đường tròn bàng tiếp là giao điểm của một đường phân giác trong và hai đường phân giác ngoài của tam giác.

Ví dụ, xét tam giác ABC, tâm của đường tròn bàng tiếp góc A là giao điểm của hai đường phân giác ngoài tại B và C, hoặc là giao điểm của đường phân giác trong góc A và đường phân giác ngoài tại B (hoặc C).

3. Các Dạng Toán Thường Gặp Về Tính Chất Hai Tiếp Tuyến Cắt Nhau

3.1. Dạng 1: Chứng Minh Các Đường Thẳng Song Song (Vuông Góc), Chứng Minh Hai Đoạn Thẳng Bằng Nhau

3.1.1. Phương Pháp Giải

• Sử dụng tính chất của hai tiếp tuyến cắt nhau: Điểm cắt nhau cách đều hai tiếp điểm, tia kẻ từ điểm cắt nhau đi qua tâm là phân giác của góc tạo bởi hai tiếp tuyến, và tia kẻ từ tâm đi qua điểm cắt nhau là phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

3.1.2. Ví dụ Minh Họa

Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ A kẻ hai tiếp tuyến AB và AC đến đường tròn (B, C là các tiếp điểm). Gọi I là trung điểm của BC. Chứng minh rằng ba điểm A, I, O thẳng hàng.

• Giải:

  • Vì AB và AC là hai tiếp tuyến của đường tròn (O) nên AB = AC (tính chất hai tiếp tuyến cắt nhau).
  • Do đó, A nằm trên đường trung trực của đoạn thẳng BC.
  • Vì OB = OC (bán kính của đường tròn) nên O cũng nằm trên đường trung trực của đoạn thẳng BC.
  • Vậy, đường thẳng AO là đường trung trực của đoạn thẳng BC.
  • Do I là trung điểm của BC nên I nằm trên đường trung trực của BC.
  • Vậy, ba điểm A, I, O thẳng hàng.

3.2. Dạng 2: Chứng Minh Một Đường Thẳng Là Tiếp Tuyến, Tính Độ Dài, Số Đo Góc và Các Yếu Tố Khác

3.2.1. Phương Pháp Giải

• Sử dụng định nghĩa tiếp tuyến: Một đường thẳng là tiếp tuyến của đường tròn nếu nó chỉ có một điểm chung với đường tròn đó.
• Áp dụng tính chất của hai tiếp tuyến cắt nhau.
• Sử dụng khái niệm đường tròn nội tiếp, bàng tiếp.
• Sử dụng hệ thức lượng về cạnh và góc trong tam giác vuông.

3.2.2. Ví dụ Minh Họa

Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn sao cho OA = 2R. Từ A kẻ các tiếp tuyến AB, AC đến đường tròn (B, C là các tiếp điểm).

a) Chứng minh tam giác ABC đều.

b) Tính độ dài đoạn BC theo R.

• Giải:

  • a) Vì AB, AC là các tiếp tuyến của (O) nên ( angle ABO = angle ACO = 90^circ ).
  • Xét tứ giác ABOC có ( angle ABO + angle ACO = 180^circ ), suy ra tứ giác ABOC nội tiếp đường tròn.
  • Theo tính chất hai tiếp tuyến cắt nhau, ta có AB = AC và AO là phân giác của ( angle BAC ).
  • Xét tam giác ABO vuông tại B, có ( sin angle BAO = frac{OB}{OA} = frac{R}{2R} = frac{1}{2} ), suy ra ( angle BAO = 30^circ ).
  • Do đó, ( angle BAC = 2 cdot angle BAO = 60^circ ).
  • Tam giác ABC có AB = AC và ( angle BAC = 60^circ ) nên tam giác ABC là tam giác đều.
  • b) Gọi I là giao điểm của AO và BC. Trong tam giác đều ABC, AI vừa là đường cao vừa là đường trung tuyến nên BI = CI và ( angle AIB = 90^circ ).
  • Xét tam giác AIB vuông tại I, có ( sin angle BAI = frac{BI}{AB} ), suy ra ( BI = AB cdot sin angle BAI = R sqrt{3} cdot sin 30^circ = frac{Rsqrt{3}}{2} ).
  • Vậy, BC = 2BI = ( Rsqrt{3} ).

4. Các Bài Tập Vận Dụng

Để củng cố kiến thức, bạn có thể thử sức với các bài tập sau:

1. Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Vẽ hai tiếp tuyến AB, AC với đường tròn (B, C là tiếp điểm). Gọi H là giao điểm của AO và BC. Chứng minh rằng BC vuông góc với AO tại H và AH.AO = AB².
2. Từ điểm A nằm ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC đến đường tròn (B, C là các tiếp điểm). Gọi D là điểm trên cung nhỏ BC. Tiếp tuyến tại D của đường tròn cắt AB, AC lần lượt tại M, N. Chứng minh rằng chu vi tam giác AMN không đổi khi D di chuyển trên cung nhỏ BC.
3. Cho tam giác ABC ngoại tiếp đường tròn (O). Gọi D, E, F là các tiếp điểm của đường tròn (O) với các cạnh BC, CA, AB. Chứng minh rằng các đường thẳng AD, BE, CF đồng quy tại một điểm.

5. Lợi Ích Khi Nắm Vững Tính Chất Hai Tiếp Tuyến Cắt Nhau

• Nâng cao kỹ năng giải toán hình học: Hiểu rõ và vận dụng thành thạo tính chất giúp bạn giải quyết các bài toán hình học một cách nhanh chóng và chính xác.
• Phát triển tư duy logic và sáng tạo: Việc áp dụng tính chất vào các bài toán khác nhau giúp bạn rèn luyện tư duy logic và khả năng sáng tạo trong giải toán.
• Xây dựng nền tảng vững chắc cho các kiến thức hình học nâng cao: Tính chất hai tiếp tuyến cắt nhau là kiến thức cơ bản, làm tiền đề cho việc học các kiến thức hình học phức tạp hơn.

Theo chia sẻ của thầy Nguyễn Văn An, giáo viên Toán tại trường THPT Chuyên Khoa học Tự nhiên, việc nắm vững kiến thức này giúp học sinh tự tin hơn khi đối mặt với các bài toán hình học trong các kỳ thi quan trọng.

6. Tại Sao Nên Sử Dụng Tài Liệu và Công Cụ Học Tập của tic.edu.vn?

• Nguồn tài liệu đa dạng và phong phú: tic.edu.vn cung cấp đầy đủ các tài liệu về tính chất hai tiếp tuyến cắt nhau, từ lý thuyết cơ bản đến các bài tập nâng cao, giúp bạn học tập một cách toàn diện.
• Thông tin được cập nhật liên tục: Các tài liệu và thông tin trên tic.edu.vn luôn được cập nhật mới nhất, đảm bảo bạn nắm bắt được những kiến thức và phương pháp giải toán tiên tiến nhất.
• Công cụ hỗ trợ học tập hiệu quả: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn ghi chú, quản lý thời gian và ôn tập kiến thức một cách hiệu quả.
• Cộng đồng học tập sôi nổi: tic.edu.vn xây dựng một cộng đồng học tập trực tuyến, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và học hỏi lẫn nhau.
• Phát triển kỹ năng: tic.edu.vn giới thiệu các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm và kỹ năng chuyên môn, hỗ trợ bạn trên con đường học tập và sự nghiệp.

7. Tối Ưu Hóa SEO và Google Discovery Cho Bài Viết

Để bài viết này xuất hiện nổi bật trên Google Discovery và ở đầu kết quả tìm kiếm, chúng tôi đã tối ưu hóa SEO bằng cách:

• Sử dụng từ khóa chính “tính chất hai tiếp tuyến cắt nhau” một cách tự nhiên và hợp lý trong tiêu đề, các tiêu đề phụ và nội dung bài viết.
• Nghiên cứu và sử dụng các từ khóa liên quan và từ khóa LSI (Latent Semantic Indexing) để mở rộng phạm vi tiếp cận của bài viết.
• Xây dựng nội dung chất lượng cao, cung cấp thông tin chi tiết, chính xác và hữu ích cho người đọc.
• Tối ưu hóa hình ảnh bằng cách sử dụng alt text mô tả và liên quan đến nội dung bài viết.
• Xây dựng cấu trúc bài viết rõ ràng, dễ đọc và dễ hiểu.
• Tăng tốc độ tải trang và đảm bảo tính thân thiện với thiết bị di động.
• Xây dựng liên kết nội bộ và liên kết bên ngoài đến các nguồn uy tín.

Theo Google Webmaster Guidelines, việc tuân thủ các nguyên tắc này giúp bài viết được đánh giá cao và hiển thị tốt hơn trên các công cụ tìm kiếm.

8. 5 Ý Định Tìm Kiếm Của Người Dùng Về Từ Khóa “Tính Chất Hai Tiếp Tuyến Cắt Nhau”

1. Định nghĩa: Người dùng muốn tìm hiểu định nghĩa chính xác của tính chất hai tiếp tuyến cắt nhau.
2. Ứng dụng: Người dùng muốn biết tính chất này được ứng dụng như thế nào trong giải toán hình học.
3. Bài tập: Người dùng muốn tìm các bài tập ví dụ và bài tập vận dụng để rèn luyện kỹ năng giải toán.
4. Chứng minh: Người dùng muốn tìm hiểu cách chứng minh các tính chất liên quan đến hai tiếp tuyến cắt nhau.
5. Liên hệ: Người dùng muốn tìm hiểu mối liên hệ giữa tính chất này với các khái niệm hình học khác như đường tròn nội tiếp, bàng tiếp.

9. Ưu Điểm Vượt Trội Của tic.edu.vn So Với Các Nguồn Tài Liệu Khác

• Đa dạng: tic.edu.vn cung cấp tài liệu cho tất cả các môn học từ lớp 1 đến lớp 12.
• Cập nhật: Thông tin và tài liệu luôn được cập nhật mới nhất theo chương trình sách giáo khoa.
• Hữu ích: Tài liệu được biên soạn bởi các chuyên gia giáo dục, đảm bảo tính chính xác và dễ hiểu.
• Cộng đồng: Cộng đồng hỗ trợ học tập sôi nổi, giúp bạn trao đổi kiến thức và kinh nghiệm.

10. Câu Hỏi Thường Gặp (FAQ)

1. Tính chất hai tiếp tuyến cắt nhau là gì?

Tính chất hai tiếp tuyến cắt nhau khẳng định rằng nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm, điểm đó cách đều hai tiếp điểm, tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến, và tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

2. Tính chất này được ứng dụng như thế nào trong giải toán?

Tính chất này được sử dụng để chứng minh các đoạn thẳng bằng nhau, các đường thẳng song song hoặc vuông góc, tính độ dài đoạn thẳng và số đo góc trong các bài toán hình học.

3. Đường tròn nội tiếp tam giác là gì?

Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác. Tâm của đường tròn nội tiếp là giao điểm của ba đường phân giác trong của tam giác.

4. Đường tròn bàng tiếp tam giác là gì?

Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và phần kéo dài của hai cạnh còn lại. Mỗi tam giác có ba đường tròn bàng tiếp.

5. Làm thế nào để chứng minh một đường thẳng là tiếp tuyến của đường tròn?

Để chứng minh một đường thẳng là tiếp tuyến của đường tròn, ta cần chứng minh rằng đường thẳng đó chỉ có một điểm chung với đường tròn.

6. Tôi có thể tìm thêm tài liệu về tính chất hai tiếp tuyến cắt nhau ở đâu trên tic.edu.vn?

Bạn có thể tìm kiếm trên tic.edu.vn bằng từ khóa “tính chất hai tiếp tuyến cắt nhau” hoặc truy cập vào mục Hình học lớp 9 để tìm các bài viết và bài tập liên quan.

7. tic.edu.vn có cung cấp công cụ hỗ trợ học tập nào không?

Có, tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến như công cụ ghi chú, quản lý thời gian và ôn tập kiến thức.

8. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn có thể đăng ký tài khoản trên tic.edu.vn và tham gia vào các diễn đàn hoặc nhóm học tập để trao đổi kiến thức và kinh nghiệm với các thành viên khác.

9. Tôi có thể liên hệ với tic.edu.vn để được tư vấn và giải đáp thắc mắc như thế nào?

Bạn có thể liên hệ với tic.edu.vn qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để biết thêm thông tin chi tiết.

10. tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu học tập khác?

tic.edu.vn cung cấp tài liệu đa dạng, cập nhật, hữu ích và có một cộng đồng hỗ trợ học tập sôi nổi, giúp bạn học tập một cách toàn diện và hiệu quả.

Bạn muốn khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả để chinh phục kiến thức về tính chất hai tiếp tuyến cắt nhau và nhiều hơn thế nữa? Hãy truy cập tic.edu.vn ngay hôm nay để trải nghiệm sự khác biệt! Liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để biết thêm chi tiết.