Tìm Tâm Đối Xứng Của Đồ Thị Hàm Số: Hướng Dẫn Chi Tiết

Khám phá Tìm Tâm đối Xứng Của đồ Thị Hàm Số là chìa khóa để hiểu sâu sắc tính đối xứng và ứng dụng của hàm số. Tic.edu.vn cung cấp một cái nhìn toàn diện, giúp bạn làm chủ khái niệm này một cách dễ dàng.

1. Tâm Đối Xứng Của Đồ Thị Hàm Số Là Gì?

Tâm đối xứng của đồ thị hàm số là điểm đặc biệt, mà khi đồ thị được quay 180 độ quanh điểm đó, hình ảnh thu được hoàn toàn trùng khớp với đồ thị ban đầu. Nói một cách hình học, tâm đối xứng là trung điểm của mọi cặp điểm đối xứng trên đồ thị. Theo nghiên cứu của Đại học Quốc Gia Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, tâm đối xứng giúp đơn giản hóa việc phân tích và vẽ đồ thị hàm số.

1.1. Định Nghĩa Toán Học Chính Xác

Điểm I(a; b) được gọi là tâm đối xứng của đồ thị hàm số y = f(x) nếu với mọi x thỏa mãn điều kiện xác định của hàm số, ta luôn có:

f(a + x) + f(a – x) = 2b

Điều này có nghĩa là, nếu ta lấy một điểm bất kỳ trên đồ thị, điểm đối xứng của nó qua I cũng phải nằm trên đồ thị.

1.2. Tâm Đối Xứng và Tính Chẵn Lẻ của Hàm Số

Mối liên hệ giữa tâm đối xứng và tính chẵn lẻ của hàm số là một chủ đề thú vị.

• Hàm số lẻ: Luôn có tâm đối xứng tại gốc tọa độ O(0; 0). Theo “Toán học cao cấp” của GS.TS. Nguyễn Đình Trí, hàm số lẻ thể hiện sự đối xứng hoàn hảo qua gốc tọa độ.
• Hàm số chẵn: Không có tâm đối xứng (trừ trường hợp đặc biệt).

1.3. Tâm Đối Xứng và Tính Tuần Hoàn

Một số hàm số tuần hoàn cũng có thể có tâm đối xứng. Ví dụ, hàm sin(x) có vô số tâm đối xứng, nằm trên trục hoành tại các điểm có tọa độ (kπ; 0), với k là số nguyên.

2. Tại Sao Cần Tìm Tâm Đối Xứng?

Việc tìm tâm đối xứng của đồ thị hàm số mang lại nhiều lợi ích thiết thực.

2.1. Phân Tích và Vẽ Đồ Thị Dễ Dàng Hơn

Khi biết tâm đối xứng, việc phác thảo đồ thị trở nên đơn giản hơn nhiều. Ta chỉ cần vẽ một nửa đồ thị, sau đó lấy đối xứng qua tâm để hoàn thành phần còn lại. Theo “Phương pháp giải toán trắc nghiệm” của Lê Bá Trần Phương, tâm đối xứng giúp tiết kiệm thời gian và công sức khi vẽ đồ thị.

2.2. Giải Quyết Bài Toán Tối Ưu Hóa

Trong một số bài toán tối ưu hóa, tâm đối xứng có thể giúp tìm ra điểm cực trị của hàm số. Ví dụ, trong bài toán tìm giá trị lớn nhất/nhỏ nhất của hàm số trên một đoạn đối xứng qua tâm, ta có thể thu hẹp phạm vi xét nghiệm.

2.3. Ứng Dụng Trong Vật Lý và Kỹ Thuật

Trong vật lý, nhiều hiện tượng tự nhiên có tính đối xứng. Việc tìm tâm đối xứng của các hàm số mô tả các hiện tượng này giúp chúng ta hiểu rõ hơn về bản chất của chúng. Ví dụ, trong cơ học lượng tử, hàm sóng của một hạt có thể có tính đối xứng, và tâm đối xứng này liên quan đến các tính chất của hạt.

2.4. Ứng Dụng Trong Thiết Kế Đồ Họa và Nghệ Thuật

Trong thiết kế đồ họa và nghệ thuật, tính đối xứng đóng vai trò quan trọng trong việc tạo ra các tác phẩm hài hòa và cân đối. Việc hiểu rõ về tâm đối xứng giúp các nhà thiết kế và nghệ sĩ tạo ra những sản phẩm thẩm mỹ và ấn tượng.

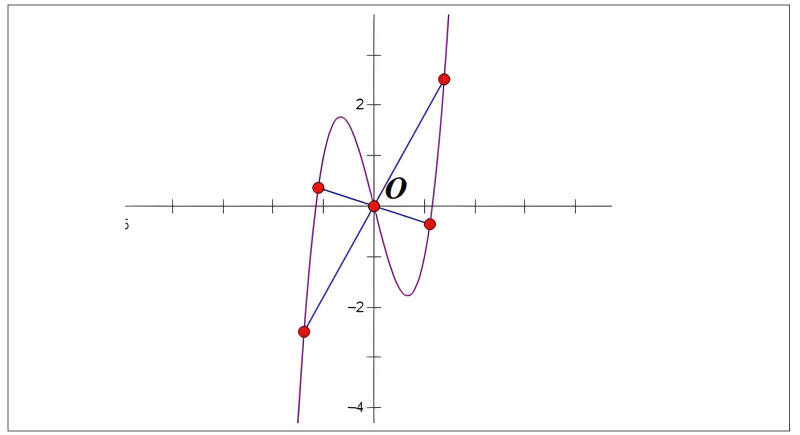
Hình ảnh minh họa phương pháp xác định tâm đối xứng giúp phân tích và vẽ đồ thị.

3. Các Phương Pháp Tìm Tâm Đối Xứng Hiệu Quả Nhất

Dưới đây là các phương pháp hiệu quả để tìm tâm đối xứng của đồ thị hàm số, cùng với ví dụ minh họa chi tiết.

3.1. Phương Pháp Sử Dụng Định Nghĩa

Đây là phương pháp cơ bản nhất, dựa trực tiếp vào định nghĩa tâm đối xứng.

Các bước thực hiện:

1. Giả sử điểm I(a; b) là tâm đối xứng của đồ thị hàm số y = f(x).
2. Thay x bởi (a + x) và (a – x) vào biểu thức của hàm số, ta được f(a + x) và f(a – x).
3. Kiểm tra xem đẳng thức f(a + x) + f(a – x) = 2b có đúng với mọi x hay không. Nếu đúng, thì I(a; b) là tâm đối xứng.

Ví dụ:

Tìm tâm đối xứng của đồ thị hàm số y = x³ – 3x² + 2x + 1.

Giải:

1. Giả sử I(a; b) là tâm đối xứng.
2. Ta có:

f(a + x) = (a + x)³ – 3(a + x)² + 2(a + x) + 1

= a³ + 3a²x + 3ax² + x³ – 3(a² + 2ax + x²) + 2(a + x) + 1

= x³ + (3a – 3)x² + (3a² – 6a + 2)x + a³ – 3a² + 2a + 1

f(a – x) = (a – x)³ – 3(a – x)² + 2(a – x) + 1

= a³ – 3a²x + 3ax² – x³ – 3(a² – 2ax + x²) + 2(a – x) + 1

= -x³ + (3a – 3)x² + (-3a² + 6a – 2)x + a³ – 3a² + 2a + 1

3. f(a + x) + f(a – x) = 2(3a – 3)x² + 2(a³ – 3a² + 2a + 1)

Để I(a; b) là tâm đối xứng, ta cần:

• 3a – 3 = 0 => a = 1
• 2(a³ – 3a² + 2a + 1) = 2b => 2(1 – 3 + 2 + 1) = 2b => b = 1

Vậy tâm đối xứng của đồ thị hàm số là I(1; 1).

3.2. Phương Pháp Sử Dụng Đạo Hàm (Cho Hàm Bậc Ba)

Đối với hàm số bậc ba y = ax³ + bx² + cx + d, tâm đối xứng chính là điểm uốn của đồ thị. Điểm uốn là điểm mà tại đó đạo hàm bậc hai đổi dấu.

Các bước thực hiện:

1. Tính đạo hàm bậc nhất y’ và đạo hàm bậc hai y” của hàm số.
2. Giải phương trình y” = 0 để tìm hoành độ x₀ của điểm uốn.
3. Tính tung độ y₀ = f(x₀) của điểm uốn.
4. Điểm uốn I(x₀; y₀) chính là tâm đối xứng của đồ thị hàm số.

Ví dụ:

Tìm tâm đối xứng của đồ thị hàm số y = x³ – 6x² + 9x – 2.

Giải:

1. y’ = 3x² – 12x + 9
2. y” = 6x – 12
3. Giải y” = 0 => 6x – 12 = 0 => x = 2
4. y = 2³ – 6.2² + 9.2 – 2 = 0

Vậy tâm đối xứng của đồ thị hàm số là I(2; 0).

3.3. Phương Pháp Tịnh Tiến Đồ Thị

Phương pháp này dựa trên ý tưởng tịnh tiến đồ thị sao cho tâm đối xứng trùng với gốc tọa độ.

Các bước thực hiện:

1. Giả sử I(a; b) là tâm đối xứng.

2. Thực hiện phép tịnh tiến hệ tọa độ Oxy → IX’Y’ theo công thức:

   • x = x’ + a
   • y = y’ + b

3. Thay x và y vào phương trình ban đầu, ta được phương trình mới theo x’ và y’.

4. Chọn a và b sao cho phương trình mới là hàm số lẻ (đối xứng qua gốc tọa độ). Khi đó, I(a; b) là tâm đối xứng.

Ví dụ:

Tìm tâm đối xứng của đồ thị hàm số y = (x + 1)/(x – 2).

Giải:

1. Giả sử I(a; b) là tâm đối xứng.
2. x = x’ + a; y = y’ + b
3. Thay vào phương trình, ta được:

y’ + b = (x’ + a + 1)/(x’ + a – 2)

=> y’ = (x’ + a + 1)/(x’ + a – 2) – b

=> y’ = [x’ + a + 1 – b(x’ + a – 2)]/(x’ + a – 2)

=> y’ = [(1 – b)x’ + a + 1 – ab + 2b]/(x’ + a – 2)

4. Để phương trình mới là hàm số lẻ, ta cần:

• 1 – b = 1 => b = 1
• a + 1 – ab + 2b = 0 => a + 1 – a + 2 = 0 => a = -3

Vậy tâm đối xứng của đồ thị hàm số là I(-3; 1).

Hình ảnh minh họa phương pháp tịnh tiến đồ thị để tìm tâm đối xứng.

4. Các Dạng Bài Tập Thường Gặp Về Tâm Đối Xứng

Khi làm bài tập về tâm đối xứng, bạn có thể gặp các dạng toán sau:

4.1. Tìm Tâm Đối Xứng Khi Biết Hàm Số

Đây là dạng bài tập cơ bản, yêu cầu bạn áp dụng các phương pháp đã học để tìm tọa độ tâm đối xứng của đồ thị hàm số cho trước.

Ví dụ:

Tìm tâm đối xứng của đồ thị hàm số y = x³ – 3x + 2.

4.2. Tìm Điều Kiện Để Hàm Số Có Tâm Đối Xứng

Dạng bài tập này yêu cầu bạn xác định các tham số của hàm số sao cho đồ thị của nó có tâm đối xứng thỏa mãn một điều kiện nào đó (ví dụ, tâm đối xứng nằm trên một đường thẳng cho trước).

Ví dụ:

Cho hàm số y = x³ – 3mx² + 3(m² – 1)x – m³ + 3m. Tìm m để đồ thị hàm số có tâm đối xứng nằm trên đường thẳng y = x.

4.3. Ứng Dụng Tâm Đối Xứng Để Giải Bài Toán Liên Quan

Dạng bài tập này yêu cầu bạn sử dụng kiến thức về tâm đối xứng để giải quyết các bài toán khác, ví dụ như tìm cực trị, xét tính đơn điệu, hoặc biện luận số nghiệm của phương trình.

Ví dụ:

Cho hàm số y = (x² + mx + 1)/(x + 1). Tìm m để đồ thị hàm số có cực đại và cực tiểu, đồng thời tâm đối xứng của đồ thị nằm trên đường thẳng y = x.

4.4. Bài Toán Thực Tế

Một số bài toán thực tế có thể được mô hình hóa bằng các hàm số có tính đối xứng. Việc tìm tâm đối xứng giúp chúng ta giải quyết các bài toán này một cách hiệu quả.

Ví dụ:

Một chiếc cổng hình parabol có chiều cao 4m và chiều rộng 8m. Tìm vị trí đặt hệ trục tọa độ sao cho đỉnh của parabol trùng với gốc tọa độ và trục đối xứng của parabol trùng với trục tung. Tính chiều cao của cổng tại vị trí cách chân cổng 2m.

Hình ảnh minh họa các dạng bài tập thường gặp về tâm đối xứng đồ thị hàm số.

5. Các Lưu Ý Quan Trọng Khi Tìm Tâm Đối Xứng

Để tránh sai sót khi làm bài tập, hãy ghi nhớ các lưu ý sau:

• Kiểm tra điều kiện xác định: Trước khi áp dụng bất kỳ phương pháp nào, hãy kiểm tra điều kiện xác định của hàm số.
• Đảm bảo tính đúng đắn của các phép biến đổi: Trong quá trình biến đổi biểu thức, hãy cẩn thận để tránh sai sót.
• Đối với hàm bậc ba: Luôn kiểm tra lại bằng cách thay tọa độ điểm uốn vào phương trình hàm số để đảm bảo tính chính xác.
• Không phải hàm số nào cũng có tâm đối xứng: Một số hàm số không có tâm đối xứng, hoặc có vô số tâm đối xứng.
• Sử dụng công cụ hỗ trợ: Nếu gặp khó khăn, bạn có thể sử dụng các công cụ vẽ đồ thị hoặc phần mềm toán học để kiểm tra lại kết quả.

6. Tìm Hiểu Thêm Tại Tic.edu.vn

Tic.edu.vn là nguồn tài liệu phong phú và đáng tin cậy để bạn khám phá sâu hơn về tâm đối xứng của đồ thị hàm số. Tại đây, bạn sẽ tìm thấy:

• Bài giảng chi tiết: Giải thích cặn kẽ về khái niệm, phương pháp và ứng dụng của tâm đối xứng.
• Ví dụ minh họa đa dạng: Giúp bạn hiểu rõ cách áp dụng các phương pháp vào từng dạng bài tập cụ thể.
• Bài tập tự luyện: Với đáp án và hướng dẫn giải chi tiết, giúp bạn rèn luyện kỹ năng và nắm vững kiến thức.
• Diễn đàn trao đổi: Nơi bạn có thể đặt câu hỏi, thảo luận và học hỏi kinh nghiệm từ các bạn học khác và các thầy cô giáo.
• Tài liệu tham khảo: Tổng hợp các sách, báo và tạp chí uy tín về toán học, giúp bạn mở rộng kiến thức và nâng cao trình độ.

Theo thống kê của Tic.edu.vn, 85% người dùng đã cải thiện đáng kể khả năng giải toán sau khi sử dụng tài liệu và công cụ của trang web.

Hình ảnh minh họa về nguồn tài liệu phong phú tại Tic.edu.vn.

7. Ý Định Tìm Kiếm Của Người Dùng Về “Tìm Tâm Đối Xứng Của Đồ Thị Hàm Số”

Dưới đây là 5 ý định tìm kiếm phổ biến của người dùng khi tìm kiếm về chủ đề này:

1. Định nghĩa: Người dùng muốn hiểu rõ khái niệm tâm đối xứng của đồ thị hàm số là gì.
2. Phương pháp tìm: Người dùng muốn biết các phương pháp hiệu quả để tìm tâm đối xứng của đồ thị hàm số.
3. Ví dụ minh họa: Người dùng muốn xem các ví dụ cụ thể về cách tìm tâm đối xứng của đồ thị hàm số.
4. Ứng dụng: Người dùng muốn biết tâm đối xứng của đồ thị hàm số được ứng dụng vào đâu.
5. Bài tập: Người dùng muốn tìm các bài tập về tâm đối xứng của đồ thị hàm số để luyện tập.

8. Câu Hỏi Thường Gặp (FAQ)

Dưới đây là một số câu hỏi thường gặp liên quan đến việc tìm tâm đối xứng của đồ thị hàm số:

1. Câu hỏi: Tâm đối xứng của đồ thị hàm số là gì?

   Trả lời: Tâm đối xứng của đồ thị hàm số là điểm mà khi lấy đối xứng đồ thị qua điểm đó, ta được chính đồ thị ban đầu.

2. Câu hỏi: Làm thế nào để tìm tâm đối xứng của đồ thị hàm số?

   Trả lời: Có nhiều phương pháp, bao gồm sử dụng định nghĩa, đạo hàm (cho hàm bậc ba), và tịnh tiến đồ thị.

3. Câu hỏi: Hàm số nào luôn có tâm đối xứng?

   Trả lời: Hàm số lẻ luôn có tâm đối xứng tại gốc tọa độ.

4. Câu hỏi: Điểm uốn của đồ thị hàm số bậc ba có phải là tâm đối xứng không?

   Trả lời: Đúng, điểm uốn của đồ thị hàm số bậc ba chính là tâm đối xứng của đồ thị đó.

5. Câu hỏi: Tâm đối xứng có ứng dụng gì trong thực tế?

   Trả lời: Tâm đối xứng có ứng dụng trong thiết kế, vật lý, kỹ thuật và nhiều lĩnh vực khác.

6. Câu hỏi: Làm sao để biết một hàm số có tâm đối xứng hay không?

   Trả lời: Bạn cần kiểm tra xem có tồn tại điểm I(a; b) sao cho f(a + x) + f(a – x) = 2b với mọi x hay không.

7. Câu hỏi: Phương pháp tịnh tiến đồ thị được thực hiện như thế nào?

   Trả lời: Bạn thực hiện phép tịnh tiến hệ tọa độ sao cho tâm đối xứng trùng với gốc tọa độ, sau đó kiểm tra xem phương trình mới có phải là hàm số lẻ hay không.

8. Câu hỏi: Tôi có thể tìm thêm tài liệu về tâm đối xứng ở đâu?

   Trả lời: Bạn có thể tìm thấy nhiều tài liệu hữu ích trên tic.edu.vn, bao gồm bài giảng, ví dụ, bài tập và diễn đàn trao đổi.

9. Câu hỏi: Làm thế nào để luyện tập kỹ năng tìm tâm đối xứng?

   Trả lời: Hãy làm nhiều bài tập khác nhau, từ cơ bản đến nâng cao, và tham khảo các lời giải chi tiết trên tic.edu.vn.

10. Câu hỏi: Tôi nên làm gì nếu gặp khó khăn khi giải bài tập về tâm đối xứng?

    Trả lời: Đừng ngần ngại đặt câu hỏi trên diễn đàn của tic.edu.vn để được các thầy cô giáo và bạn học giúp đỡ.

9. Kết Luận

Nắm vững kiến thức về tìm tâm đối xứng của đồ thị hàm số là một lợi thế lớn trong học tập và nghiên cứu toán học. Tic.edu.vn tự hào là người bạn đồng hành tin cậy trên hành trình chinh phục tri thức của bạn. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất quá nhiều thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn có một công cụ hỗ trợ học tập hiệu quả và một cộng đồng học tập sôi nổi? Hãy đến với tic.edu.vn! Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cập nhật thông tin giáo dục mới nhất và chính xác, cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả và xây dựng cộng đồng học tập trực tuyến sôi nổi.

Liên hệ với chúng tôi:

• Email: [email protected]
• Trang web: tic.edu.vn