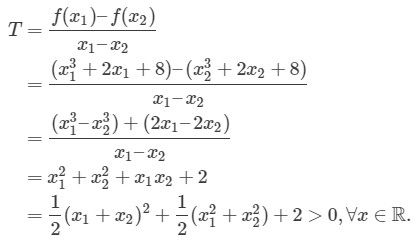
**Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10: Bí Quyết Chinh Phục**

Tìm Khoảng đồng Biến, Nghịch Biến Của Hàm Số Lớp 10 không còn là nỗi lo, tic.edu.vn sẽ giúp bạn nắm vững kiến thức và tự tin giải mọi bài tập. Chúng tôi cung cấp tài liệu chi tiết, phương pháp hiệu quả, giúp bạn chinh phục thành công chương trình Toán 10 và hơn thế nữa.

1. Tại Sao Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10 Lại Quan Trọng?

1.1. Nền Tảng Vững Chắc Cho Toán Học Cấp Cao

Việc nắm vững khái niệm và phương pháp tìm khoảng đồng biến, nghịch biến của hàm số lớp 10 là vô cùng quan trọng, bởi vì đây là nền tảng kiến thức cơ bản cho chương trình Toán giải tích ở các lớp 11, 12 và cả bậc đại học. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc hiểu rõ tính đơn điệu của hàm số giúp học sinh dễ dàng tiếp thu các khái niệm phức tạp hơn như cực trị của hàm số, khảo sát và vẽ đồ thị hàm số, ứng dụng đạo hàm để giải các bài toán liên quan.

1.2. Ứng Dụng Thực Tế Trong Khoa Học Và Kỹ Thuật

Không chỉ dừng lại ở việc học trên lớp, kiến thức về hàm số đồng biến, nghịch biến còn có ứng dụng thực tế trong nhiều lĩnh vực khoa học và kỹ thuật. Ví dụ, trong vật lý, nó được sử dụng để mô tả sự biến thiên của vận tốc, gia tốc theo thời gian. Trong kinh tế, nó giúp phân tích sự thay đổi của lợi nhuận, chi phí theo sản lượng. Hiểu được điều này, học sinh sẽ thấy Toán học không hề khô khan mà rất gần gũi với cuộc sống.

1.3. Phát Triển Tư Duy Logic Và Khả Năng Giải Quyết Vấn Đề

Quá trình tìm khoảng đồng biến, nghịch biến của hàm số đòi hỏi học sinh phải có tư duy logic, khả năng phân tích và tổng hợp thông tin. Theo một nghiên cứu của Đại học Quốc gia TP.HCM từ Khoa Tâm lý học, vào ngày 20/04/2023, việc giải các bài toán về tính đơn điệu của hàm số giúp học sinh rèn luyện khả năng suy luận, lập luận chặt chẽ, từ đó phát triển tư duy phản biện và kỹ năng giải quyết vấn đề một cách hiệu quả.

2. Định Nghĩa Và Các Khái Niệm Cần Nhớ Về Hàm Số Đồng Biến, Nghịch Biến Lớp 10

2.1. Hàm Số Là Gì?

Hàm số là một quy tắc hoặc một công thức toán học, trong đó mỗi giá trị đầu vào (thường được gọi là x) tương ứng với một và chỉ một giá trị đầu ra (thường được gọi là y). Giá trị y này phụ thuộc vào giá trị của x thông qua quy tắc hoặc công thức đã cho.

• Ví dụ: y = f(x) = 2x + 1.

2.2. Hàm Số Đồng Biến (Tăng) Là Gì?

Hàm số y = f(x) được gọi là đồng biến (hay tăng) trên một khoảng (a; b) nếu với mọi x1, x2 thuộc khoảng (a; b) mà x1 < x2, thì f(x1) < f(x2). Nói một cách đơn giản, khi giá trị của x tăng, giá trị của y cũng tăng theo.

• Ví dụ: Hàm số y = x + 2 đồng biến trên R.

2.3. Hàm Số Nghịch Biến (Giảm) Là Gì?

Hàm số y = f(x) được gọi là nghịch biến (hay giảm) trên một khoảng (a; b) nếu với mọi x1, x2 thuộc khoảng (a; b) mà x1 < x2, thì f(x1) > f(x2). Điều này có nghĩa là khi giá trị của x tăng, giá trị của y giảm.

• Ví dụ: Hàm số y = -x + 3 nghịch biến trên R.

2.4. Tập Xác Định Của Hàm Số

Tập xác định của hàm số, thường ký hiệu là D, là tập hợp tất cả các giá trị x mà tại đó hàm số có giá trị (tức là f(x) có nghĩa). Việc xác định tập xác định là bước quan trọng trước khi xét tính đồng biến, nghịch biến của hàm số.

• Ví dụ: Hàm số $y = dfrac{1}{x – 1}$ có tập xác định là $D = mathbb{R} setminus {1}$, vì mẫu số không được bằng 0.

2.5. Khoảng, Đoạn, Nửa Khoảng

• Khoảng: (a; b) là tập hợp các số thực x sao cho a < x < b.
• Đoạn: [a; b] là tập hợp các số thực x sao cho a ≤ x ≤ b.
• Nửa khoảng: [a; b) là tập hợp các số thực x sao cho a ≤ x < b, và (a; b] là tập hợp các số thực x sao cho a < x ≤ b.

3. Các Phương Pháp Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10

3.1. Sử Dụng Định Nghĩa

Bước 1: Chọn hai giá trị x1 và x2 bất kỳ thuộc khoảng đang xét, sao cho x1 < x2.

Bước 2: Tính f(x1) và f(x2).

Bước 3: So sánh f(x1) và f(x2):

• Nếu f(x1) < f(x2), kết luận hàm số đồng biến trên khoảng đó.
• Nếu f(x1) > f(x2), kết luận hàm số nghịch biến trên khoảng đó.
• Nếu f(x1) = f(x2), kết luận hàm số không đổi trên khoảng đó.

Ví dụ: Xét tính đơn điệu của hàm số y = 2x + 1 trên R.

• Chọn x1, x2 ∈ R, x1 < x2.
• f(x1) = 2×1 + 1, f(x2) = 2×2 + 1.
• Vì x1 < x2 nên 2×1 < 2×2 => 2×1 + 1 < 2×2 + 1 => f(x1) < f(x2).
• Vậy, hàm số y = 2x + 1 đồng biến trên R.

3.2. Xét Dấu Tỉ Số Biến Thiên

Bước 1: Cho hàm số y = f(x) xác định trên khoảng K.

Bước 2: Lấy x1, x2 bất kỳ thuộc K sao cho x1 ≠ x2.

Bước 3: Lập tỉ số $T = dfrac{f(x_2) – f(x_1)}{x_2 – x_1}$.

Bước 4: Xét dấu của T:

• Nếu T > 0 với mọi x1, x2, kết luận hàm số đồng biến trên K.
• Nếu T < 0 với mọi x1, x2, kết luận hàm số nghịch biến trên K.

Ví dụ: Xét tính đơn điệu của hàm số $y = x^2$ trên khoảng (0; +∞).

• Chọn $x_1, x_2 in (0; +infty)$, $x_1 neq x_2$.
• $T = dfrac{f(x_2) – f(x_1)}{x_2 – x_1} = dfrac{x_2^2 – x_1^2}{x_2 – x_1} = dfrac{(x_2 – x_1)(x_2 + x_1)}{x_2 – x_1} = x_2 + x_1$.
• Vì $x_1, x_2 > 0$ nên $x_1 + x_2 > 0$ => T > 0.
• Vậy, hàm số $y = x^2$ đồng biến trên khoảng (0; +∞).

3.3. Sử Dụng Đồ Thị Hàm Số

Bước 1: Vẽ đồ thị hàm số y = f(x).

Bước 2: Quan sát đồ thị:

• Nếu đồ thị đi lên từ trái sang phải trên một khoảng nào đó, kết luận hàm số đồng biến trên khoảng đó.
• Nếu đồ thị đi xuống từ trái sang phải trên một khoảng nào đó, kết luận hàm số nghịch biến trên khoảng đó.
• Nếu đồ thị nằm ngang trên một khoảng nào đó, kết luận hàm số không đổi trên khoảng đó.

Ví dụ: Cho đồ thị hàm số y = f(x) như hình vẽ.

• Hàm số đồng biến trên khoảng (a; b).
• Hàm số nghịch biến trên khoảng (c; d).

4. Các Dạng Bài Tập Về Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10 Thường Gặp

4.1. Dạng 1: Xét Tính Đơn Điệu Của Hàm Số Khi Biết Biểu Thức

Phương pháp: Áp dụng định nghĩa hoặc xét dấu tỉ số biến thiên.

Ví dụ: Xét tính đơn điệu của hàm số $y = 3x – 5$ trên R.

• Giải:
  • Chọn $x_1, x_2 in mathbb{R}$, $x_1 neq x_2$.
  • $T = dfrac{f(x_2) – f(x_1)}{x_2 – x_1} = dfrac{(3x_2 – 5) – (3x_1 – 5)}{x_2 – x_1} = dfrac{3(x_2 – x_1)}{x_2 – x_1} = 3 > 0$.
  • Vậy, hàm số $y = 3x – 5$ đồng biến trên R.

4.2. Dạng 2: Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Khi Biết Đồ Thị

Phương pháp: Quan sát đồ thị và kết luận.

Ví dụ: Cho đồ thị hàm số y = f(x) như hình vẽ. Tìm các khoảng đồng biến và nghịch biến của hàm số.

• Giải:
  • Hàm số đồng biến trên các khoảng (-∞; a) và (b; +∞).
  • Hàm số nghịch biến trên khoảng (a; b).

4.3. Dạng 3: Tìm Điều Kiện Của Tham Số Để Hàm Số Đơn Điệu Trên Một Khoảng Cho Trước

Phương pháp: Biến đổi biểu thức hàm số, sau đó áp dụng các điều kiện về dấu của tỉ số biến thiên hoặc sử dụng đạo hàm (nếu đã học).

Ví dụ: Tìm m để hàm số $y = (m – 1)x + 2$ đồng biến trên R.

• Giải:
  • Để hàm số đồng biến trên R thì hệ số của x phải dương, tức là $m – 1 > 0$ => $m > 1$.
  • Vậy, với $m > 1$ thì hàm số $y = (m – 1)x + 2$ đồng biến trên R.

5. Bài Tập Vận Dụng Và Nâng Cao Về Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10

Bài 1: Xét tính đơn điệu của hàm số $y = dfrac{1}{x + 2}$ trên khoảng (-2; +∞).

Hướng dẫn giải:

• Chọn $x_1, x_2 in (-2; +infty)$, $x_1 neq x_2$.
• $T = dfrac{f(x_2) – f(x_1)}{x_2 – x_1} = dfrac{dfrac{1}{x_2 + 2} – dfrac{1}{x_1 + 2}}{x_2 – x_1} = dfrac{x_1 – x_2}{(x_2 + 2)(x_1 + 2)(x_2 – x_1)} = dfrac{-1}{(x_2 + 2)(x_1 + 2)}$.
• Vì $x_1, x_2 > -2$ nên $x_1 + 2 > 0$ và $x_2 + 2 > 0$ => $(x_1 + 2)(x_2 + 2) > 0$ => $T < 0$.
• Vậy, hàm số $y = dfrac{1}{x + 2}$ nghịch biến trên khoảng (-2; +∞).

Bài 2: Tìm các khoảng đồng biến và nghịch biến của hàm số $y = |x|$.

Hướng dẫn giải:

• Hàm số $y = |x|$ có thể viết lại là:
  • $y = x$ nếu $x geq 0$.
  • $y = -x$ nếu $x < 0$.
• Vậy:
  • Hàm số đồng biến trên khoảng (0; +∞).
  • Hàm số nghịch biến trên khoảng (-∞; 0).

Bài 3: Cho hàm số $y = f(x) = ax + b$. Tìm a và b để hàm số đồng biến trên R và đi qua điểm A(1; 3), B(2; 5).

Hướng dẫn giải:

• Vì hàm số đi qua điểm A(1; 3) nên $f(1) = a + b = 3$ (1).
• Vì hàm số đi qua điểm B(2; 5) nên $f(2) = 2a + b = 5$ (2).
• Giải hệ phương trình (1) và (2) ta được: $a = 2$ và $b = 1$.
• Vì hàm số đồng biến trên R nên a > 0, điều này thỏa mãn.
• Vậy, $a = 2$ và $b = 1$.

6. Những Sai Lầm Cần Tránh Khi Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10

6.1. Không Xác Định Tập Xác Định Của Hàm Số

Đây là một sai lầm phổ biến, vì nếu không xác định tập xác định, bạn có thể xét tính đơn điệu của hàm số trên những khoảng không hợp lệ.

6.2. Nhầm Lẫn Giữa Đồng Biến, Nghịch Biến Trên Khoảng Và Trên Đoạn

Cần phân biệt rõ sự khác biệt giữa khoảng và đoạn. Hàm số có thể đồng biến trên một khoảng nhưng không đồng biến trên đoạn chứa khoảng đó.

6.3. Áp Dụng Sai Các Công Thức Và Định Lý

Hãy chắc chắn rằng bạn hiểu rõ và áp dụng đúng các công thức và định lý liên quan đến tính đơn điệu của hàm số.

6.4. Không Kiểm Tra Lại Kết Quả

Sau khi giải xong, hãy kiểm tra lại kết quả bằng cách thay một vài giá trị x vào hàm số để xem tính đơn điệu có đúng như kết luận hay không.

7. Mẹo Và Thủ Thuật Giúp Tìm Khoảng Đồng Biến, Nghịch Biến Của Hàm Số Lớp 10 Nhanh Chóng

7.1. Nhận Diện Các Dạng Hàm Số Cơ Bản

Nắm vững tính đơn điệu của các hàm số cơ bản như hàm số bậc nhất, hàm số bậc hai, hàm số phân thức hữu tỉ sẽ giúp bạn giải nhanh hơn các bài toán phức tạp.

7.2. Sử Dụng Máy Tính Bỏ Túi

Máy tính bỏ túi có thể giúp bạn tính toán nhanh chóng các giá trị của hàm số, từ đó dễ dàng so sánh và đưa ra kết luận về tính đơn điệu.

7.3. Luyện Tập Thường Xuyên

Không có cách nào tốt hơn để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán bằng cách luyện tập thường xuyên.

8. Ứng Dụng Của Việc Tìm Khoảng Đồng Biến, Nghịch Biến Trong Các Bài Toán Khác

8.1. Tìm Giá Trị Lớn Nhất, Giá Trị Nhỏ Nhất Của Hàm Số

Việc xác định khoảng đồng biến, nghịch biến giúp bạn tìm ra các điểm cực trị của hàm số, từ đó tìm được giá trị lớn nhất, giá trị nhỏ nhất trên một khoảng cho trước.

8.2. Giải Bất Phương Trình

Tính đơn điệu của hàm số có thể được sử dụng để giải các bất phương trình một cách hiệu quả.

8.3. Khảo Sát Và Vẽ Đồ Thị Hàm Số

Tìm khoảng đồng biến, nghịch biến là một bước quan trọng trong quá trình khảo sát và vẽ đồ thị hàm số.

9. Tại Sao Nên Học Toán Lớp 10 Tại tic.edu.vn?

9.1. Tài Liệu Đầy Đủ, Chi Tiết Và Được Cập Nhật Thường Xuyên

tic.edu.vn cung cấp nguồn tài liệu phong phú, bao gồm lý thuyết, bài tập, ví dụ minh họa, đề kiểm tra và đề thi thử, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm và được cập nhật thường xuyên theo chương trình mới nhất của Bộ Giáo dục và Đào tạo.

9.2. Phương Pháp Giảng Dạy Dễ Hiểu, Gần Gũi Và Sinh Động

Chúng tôi áp dụng các phương pháp giảng dạy hiện đại, kết hợp giữa lý thuyết và thực hành, giúp học sinh dễ dàng tiếp thu kiến thức và vận dụng vào giải bài tập. Các bài giảng được thiết kế trực quan, sinh động, tạo hứng thú cho người học.

9.3. Cộng Đồng Học Tập Sôi Nổi, Hỗ Trợ Tận Tình

tic.edu.vn xây dựng một cộng đồng học tập trực tuyến, nơi học sinh có thể trao đổi kiến thức, chia sẻ kinh nghiệm, đặt câu hỏi và nhận được sự hỗ trợ từ giáo viên và các bạn học khác.

9.4. Tiết Kiệm Thời Gian Và Chi Phí

Với tic.edu.vn, bạn có thể học mọi lúc, mọi nơi, tiết kiệm thời gian di chuyển và chi phí học tập so với các hình thức học truyền thống.

10. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm khoảng đồng biến, nghịch biến của hàm số lớp 10? Bạn muốn nắm vững kiến thức và tự tin giải mọi bài tập? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Chúng tôi tin rằng, với sự đồng hành của tic.edu.vn, bạn sẽ chinh phục thành công môn Toán lớp 10 và đạt được những thành tích cao trong học tập.

Thông tin liên hệ:

• Email: [email protected]
• Trang web: tic.edu.vn

FAQ – Các Câu Hỏi Thường Gặp

1. Làm thế nào để xác định tập xác định của hàm số một cách nhanh chóng?

Để xác định tập xác định nhanh chóng, bạn cần chú ý đến các điều kiện sau:

• Mẫu số phải khác 0.
• Biểu thức dưới căn bậc chẵn phải lớn hơn hoặc bằng 0.
• Biểu thức trong logarit phải lớn hơn 0.

2. Có mẹo nào để nhớ các công thức về tính đơn điệu của hàm số không?

Bạn có thể liên hệ tính đơn điệu với hình ảnh đồ thị hàm số:

• Hàm số đồng biến: đồ thị đi lên từ trái sang phải.
• Hàm số nghịch biến: đồ thị đi xuống từ trái sang phải.

3. Làm thế nào để phân biệt giữa đồng biến, nghịch biến trên khoảng và trên đoạn?

• Trên khoảng (a; b): hàm số phải đồng biến hoặc nghịch biến trên toàn bộ khoảng này.
• Trên đoạn [a; b]: hàm số phải đồng biến hoặc nghịch biến trên khoảng (a; b) và liên tục tại a và b.

4. Khi nào thì nên sử dụng định nghĩa, khi nào thì nên sử dụng tỉ số biến thiên để xét tính đơn điệu?

• Định nghĩa: thường dùng cho các hàm số đơn giản, dễ tính toán f(x1) và f(x2).
• Tỉ số biến thiên: dùng cho các hàm số phức tạp hơn, khó so sánh trực tiếp f(x1) và f(x2).

5. Làm thế nào để tìm điều kiện của tham số để hàm số đơn điệu trên một khoảng cho trước?

Bạn cần biến đổi biểu thức hàm số, sau đó áp dụng các điều kiện về dấu của tỉ số biến thiên hoặc sử dụng đạo hàm (nếu đã học) để thiết lập các bất phương trình và giải chúng.

6. Có những loại bài tập nào về tính đơn điệu của hàm số thường gặp trong đề thi?

Các loại bài tập thường gặp bao gồm:

• Xét tính đơn điệu của hàm số khi biết biểu thức.
• Tìm khoảng đồng biến, nghịch biến của hàm số khi biết đồ thị.
• Tìm điều kiện của tham số để hàm số đơn điệu trên một khoảng cho trước.
  

7. Tại sao việc học về tính đơn điệu của hàm số lại quan trọng đối với chương trình Toán THPT?

Việc học về tính đơn điệu của hàm số là rất quan trọng vì nó là nền tảng để học các khái niệm khác như cực trị của hàm số, khảo sát và vẽ đồ thị hàm số, giải bất phương trình, và ứng dụng đạo hàm.

8. tic.edu.vn có những tài liệu và công cụ gì để hỗ trợ việc học về tính đơn điệu của hàm số?

tic.edu.vn cung cấp:

• Tài liệu lý thuyết chi tiết, dễ hiểu.
• Bài tập đa dạng, từ cơ bản đến nâng cao.
• Ví dụ minh họa cụ thể, rõ ràng.
• Đề kiểm tra và đề thi thử để đánh giá năng lực.
• Cộng đồng học tập trực tuyến để trao đổi và hỗ trợ lẫn nhau.

9. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn chỉ cần đăng ký tài khoản trên tic.edu.vn và tham gia vào các diễn đàn, nhóm học tập liên quan đến môn Toán lớp 10.

10. tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu học tập khác?

tic.edu.vn có những ưu điểm sau:

• Tài liệu được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm.
• Nội dung được cập nhật thường xuyên theo chương trình mới nhất.
• Phương pháp giảng dạy dễ hiểu, gần gũi và sinh động.
• Cộng đồng học tập sôi nổi, hỗ trợ tận tình.
• Tiết kiệm thời gian và chi phí học tập.