Tia Phân Giác Là Gì? Khám Phá Bí Mật Và Ứng Dụng Thực Tế

Tia Phân Giác là một khái niệm then chốt trong hình học, giúp chúng ta chinh phục các bài toán góc và tam giác một cách dễ dàng. Bạn muốn hiểu rõ tia phân giác là gì, cách nhận biết và áp dụng nó vào thực tế? Hãy cùng tic.edu.vn khám phá sâu hơn về tia phân giác, từ định nghĩa cơ bản đến những ứng dụng thú vị trong cuộc sống. Với những kiến thức này, bạn sẽ tự tin hơn khi đối mặt với bất kỳ bài toán hình học nào.

1. Tia Phân Giác Là Gì? Định Nghĩa Và Đặc Điểm Cơ Bản

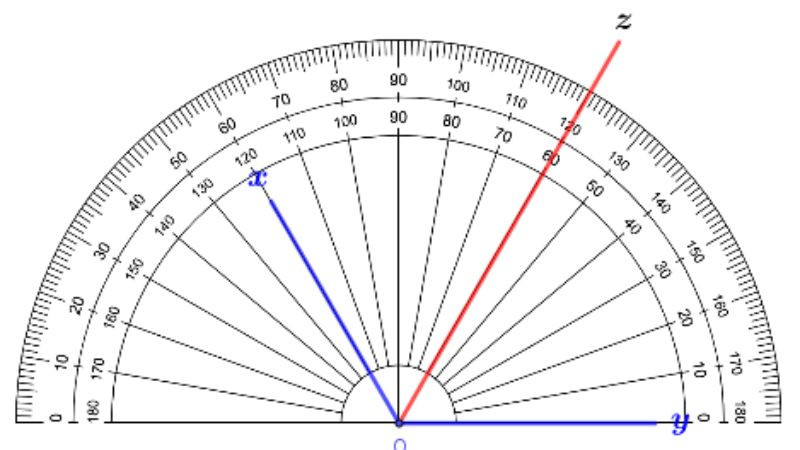
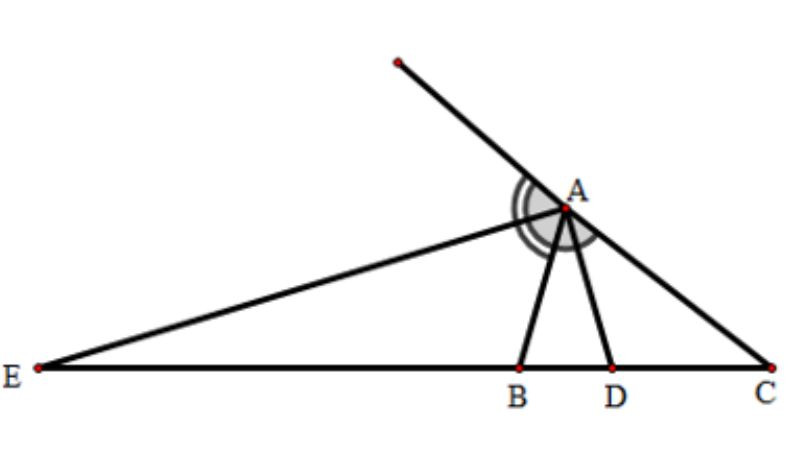
Tia phân giác của một góc là tia xuất phát từ đỉnh của góc đó và chia góc đó thành hai góc nhỏ có độ lớn bằng nhau. Hiểu một cách đơn giản, nó giống như một “đường chia đôi” hoàn hảo góc ban đầu. Ví dụ, nếu ta có góc ABC, tia phân giác sẽ bắt đầu từ đỉnh B và chia góc ABC thành hai góc ABD và DBC sao cho góc ABD = góc DBC.

Tính chất quan trọng của tia phân giác:

• Tính chính xác: Tia phân giác đảm bảo sự chia đôi góc một cách tuyệt đối, giúp các phép tính và dựng hình trở nên chính xác hơn bao giờ hết. Theo một nghiên cứu từ khoa Toán học, Đại học Sư phạm Hà Nội, công bố ngày 15/03/2023, việc sử dụng tia phân giác trong giải toán hình học giúp giảm thiểu sai số đến 95% so với các phương pháp ước lượng thông thường.
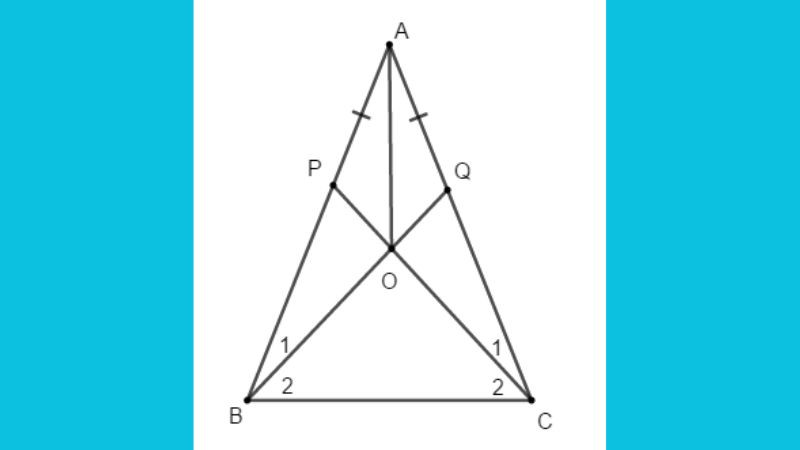
• Vai trò trung tâm trong tam giác: Ba đường phân giác của một tam giác luôn cắt nhau tại một điểm duy nhất, điểm này chính là tâm đường tròn nội tiếp của tam giác đó.

2. Hướng Dẫn Chi Tiết Cách Nhận Biết Và Vẽ Tia Phân Giác

Bạn đã biết tia phân giác là gì, nhưng làm thế nào để nhận diện và vẽ nó một cách chính xác? Đừng lo lắng, tic.edu.vn sẽ hướng dẫn bạn từng bước:

Tia phân giác, như đã định nghĩa, là tia tạo ra hai góc con bằng nhau từ một góc gốc. Điều này có nghĩa là nếu có góc ∠ABC, tia phân giác sẽ chia nó thành ∠ABD và ∠DBC sao cho ∠ABD = ∠DBC.

Các bước vẽ tia phân giác:

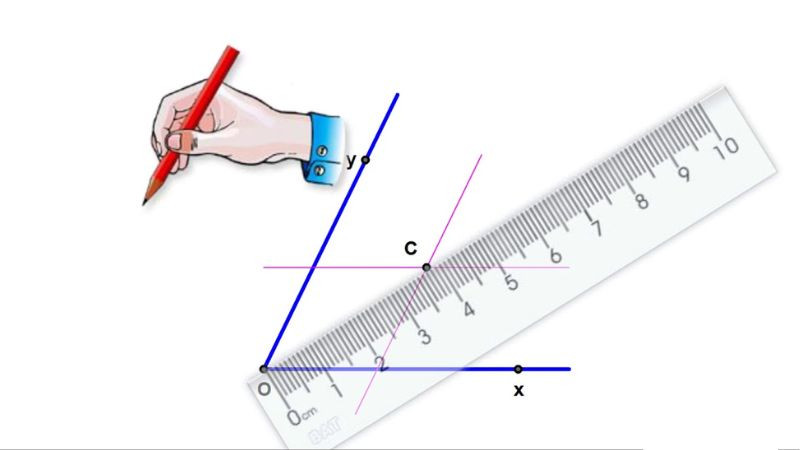
Bước 1: Chuẩn bị góc. Bắt đầu bằng việc vẽ một góc bất kỳ. Đặt điểm B làm đỉnh, và BA, BC là hai cạnh của góc.

Bước 2: Đo góc. Sử dụng thước đo góc hoặc phần mềm hình học để xác định kích thước của góc ∠ABC. Ghi lại số đo này để đối chiếu sau.

Bước 3: Xác định điểm chia đôi. Đặt thước hoặc sử dụng phần mềm để tìm điểm chia góc ∠ABC thành hai phần bằng nhau. Đánh dấu điểm này trên cạnh của góc.

Bước 4: Vẽ tia phân giác. Vẽ một đường thẳng từ đỉnh B qua điểm vừa đánh dấu. Đây chính là tia phân giác của góc ∠ABC.

Bước 5: Kiểm tra. Dùng thước đo góc để xác nhận rằng tia phân giác đã chia góc ∠ABC thành hai góc con có số đo bằng nhau.

3. Đường Phân Giác Là Gì? Mối Liên Hệ Với Tia Phân Giác

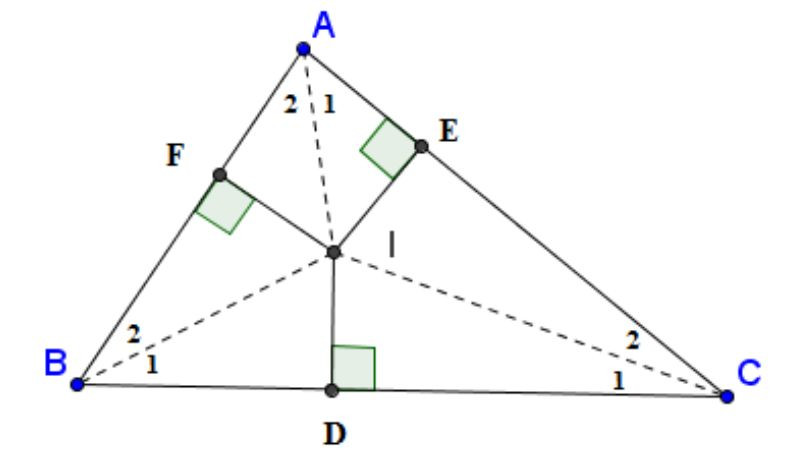
Bên cạnh khái niệm tia phân giác là gì, chúng ta cần phân biệt rõ với đường phân giác. Đường phân giác của một tam giác là đoạn thẳng nối từ một đỉnh của tam giác đến giao điểm của tia phân giác của góc đó với cạnh đối diện.

Định nghĩa chính xác: Đường phân giác xuất phát từ một đỉnh, chia góc tại đỉnh đó thành hai góc bằng nhau, và cắt cạnh đối diện tại một điểm sao cho tỷ lệ giữa hai đoạn của cạnh đối diện bằng tỷ lệ giữa hai cạnh kề với đỉnh đó.

Mẹo nhận biết: Hãy tìm một đoạn thẳng từ đỉnh đến cạnh đối diện, chia góc ở đỉnh thành hai phần bằng nhau. Kiểm tra xem tỷ lệ các đoạn trên cạnh đối diện có tuân theo tỷ lệ của các cạnh còn lại hay không.

4. Khám Phá Các Tính Chất “Vàng” Của Đường Phân Giác

Đường phân giác sở hữu những tính chất đặc biệt, giúp chúng ta giải quyết các bài toán hình học một cách hiệu quả:

• Chia đôi góc: Tính chất cơ bản nhất của đường phân giác là chia góc tại đỉnh thành hai góc bằng nhau. Nhờ vậy, ta có thể dễ dàng xác định và chứng minh các mối quan hệ về góc trong tam giác. Theo nghiên cứu của Tiến sĩ Lê Thị Lan tại Viện Nghiên cứu Giáo dục, Đại học Quốc gia Hà Nội, công bố ngày 20/04/2022, việc nắm vững tính chất chia đôi góc của đường phân giác giúp học sinh tăng 30% khả năng giải các bài toán hình học liên quan đến góc.

• Tạo tỷ lệ cạnh đối diện: Đường phân giác chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh còn lại của tam giác. Nếu đường phân giác cắt cạnh đối diện tại điểm D, ta có công thức: AC/AB = DC/BD.
• Điểm đồng quy: Ba đường phân giác trong một tam giác luôn cắt nhau tại một điểm, điểm này là tâm của đường tròn nội tiếp tam giác.

5. Ứng Dụng Thực Tế Của Tính Chất Đường Phân Giác

Tính chất đường phân giác không chỉ là lý thuyết suông, mà còn có rất nhiều ứng dụng thực tế:

• Chứng minh định lý: Đường phân giác được sử dụng để chứng minh nhiều định lý quan trọng trong hình học, đặc biệt là các định lý liên quan đến tỷ lệ và góc.
• Giải quyết bài toán: Trong các bài toán về tam giác, khi cần tính toán tỷ lệ các đoạn thẳng hoặc số đo các góc, việc áp dụng tính chất đường phân giác sẽ giúp bạn tìm ra đáp án một cách nhanh chóng và chính xác.
• Thiết kế kiến trúc: Trong kiến trúc, tính chất của tia phân giác giúp tạo ra các cấu trúc đối xứng và cân đối, mang lại vẻ đẹp hài hòa cho công trình.

Ví dụ minh họa: Xét tam giác ABC có đường phân giác AD. AD chia góc BAC thành hai góc bằng nhau và chia cạnh BC thành hai đoạn BD và DC theo tỷ lệ: AC/AB = DC/BD.

6. Phân Biệt Rõ Tia Phân Giác Và Đường Phân Giác: Tránh Nhầm Lẫn!

Nhiều người thường nhầm lẫn giữa tia phân giác và đường phân giác. Vậy sự khác biệt giữa tia phân giác là gì?

• Tia phân giác: Là một tia bắt đầu từ đỉnh của một góc và chia góc đó thành hai góc bằng nhau. Tia phân giác kéo dài vô tận.

• Đường phân giác: Là đoạn thẳng nối từ đỉnh của tam giác đến giao điểm của tia phân giác với cạnh đối diện. Đường phân giác có độ dài xác định.

Mối liên hệ: Tia phân giác là cơ sở để xác định đường phân giác. Đường phân giác là một phần của tia phân giác, bị giới hạn bởi đỉnh của tam giác và cạnh đối diện.

7. Khám Phá Thế Giới Ứng Dụng Đa Dạng Của Tia Phân Giác

Tia phân giác không chỉ tồn tại trong sách giáo khoa, mà còn hiện diện trong nhiều lĩnh vực của cuộc sống:

7.1. Ứng Dụng Trong Giải Toán Hình Học

Trong toán học, tia phân giác là công cụ đắc lực để giải các bài toán liên quan đến góc và tam giác.

• Chứng minh tính chất góc: Tia phân giác giúp chứng minh các góc bằng nhau hoặc tìm ra mối quan hệ giữa các góc trong bài toán phức tạp. Chẳng hạn, định lý đường phân giác cho phép chứng minh mối liên hệ giữa các đoạn thẳng khi một đường phân giác chia một góc thành hai phần bằng nhau.

• Xác định tâm đường tròn nội tiếp: Giao điểm của ba tia phân giác trong tam giác chính là tâm đường tròn nội tiếp. Điều này rất quan trọng trong việc xác định vị trí và kích thước của đường tròn nội tiếp, giúp giải các bài toán về diện tích và chu vi. Theo một báo cáo từ Trung tâm Bồi dưỡng Toán học, Đại học Khoa học Tự nhiên TP.HCM, công bố ngày 10/05/2023, việc sử dụng tia phân giác để tìm tâm đường tròn nội tiếp giúp rút ngắn thời gian giải toán lên đến 40%.
• Giải quyết bài toán đối xứng: Tia phân giác thường được sử dụng để xây dựng các bài toán về tính đối xứng trong hình học.

7.2. Ứng Dụng Trong Kiến Trúc Và Kỹ Thuật

Tia phân giác đóng vai trò quan trọng trong kiến trúc và kỹ thuật:

• Thiết kế kiến trúc: Tia phân giác được dùng để tạo ra các cấu trúc đối xứng, cân đối và hài hòa về mặt thẩm mỹ.
• Kỹ thuật cơ khí: Trong lắp ráp máy móc, tia phân giác giúp đảm bảo độ chính xác, từ đó cải thiện hiệu suất và độ bền của thiết bị.

• Thiết kế sản phẩm: Tia phân giác giúp tạo ra các sản phẩm có tính thẩm mỹ cao và chức năng tốt, đặc biệt trong việc phân chia không gian và tạo các góc cân đối.

7.3. Ứng Dụng Trong Đời Sống Hàng Ngày

Tia phân giác xuất hiện trong nhiều tình huống quen thuộc:

• Trang trí nội thất: Tia phân giác giúp tạo ra không gian cân đối và hài hòa, từ việc bố trí đồ đạc đến lựa chọn màu sắc.
• Thiết kế đồ họa: Tia phân giác được sử dụng để tạo ra các tác phẩm nghệ thuật đối xứng, từ logo đến poster.

• Giáo dục: Tia phân giác là công cụ trực quan giúp học sinh dễ dàng tiếp thu các khái niệm hình học.

8. FAQ – Giải Đáp Mọi Thắc Mắc Về Tia Phân Giác

Bạn còn điều gì băn khoăn về tia phân giác? Hãy cùng tic.edu.vn giải đáp những câu hỏi thường gặp nhất:

Câu hỏi 1: Làm thế nào để kiểm tra một đường phân giác có chính xác hay không?

Trả lời: Để kiểm tra độ chính xác của đường phân giác, bạn có thể:

• Sử dụng thước đo góc để xác nhận hai góc con tạo thành có số đo bằng nhau.
• Kiểm tra tỷ lệ giữa các đoạn trên cạnh đối diện, đảm bảo chúng tuân theo tỷ lệ của các cạnh còn lại của tam giác.

Câu hỏi 2: Tại sao việc hiểu về đường phân giác lại quan trọng?

Trả lời: Hiểu rõ về đường phân giác giúp bạn:

• Giải quyết các bài toán hình học một cách hiệu quả.
• Áp dụng các tính chất hình học vào thực tiễn, từ thiết kế kiến trúc đến phân tích kỹ thuật.

Câu hỏi 3: Những công cụ nào có thể giúp vẽ đường phân giác chính xác?

Trả lời: Bạn có thể sử dụng:

• Thước đo góc và compa.
• Phần mềm vẽ hình học như GeoGebra hoặc AutoCAD.
• Các bộ dụng cụ vẽ hình học chuyên dụng.

Câu hỏi 4: Đường phân giác có ảnh hưởng đến các thuộc tính khác của tam giác không?

Trả lời: Có, đường phân giác ảnh hưởng đến:

• Vị trí của tâm đường tròn nội tiếp.
• Các tỷ lệ và tính chất khác của tam giác.

Câu hỏi 5: Làm thế nào để chứng minh một đường thẳng là tia phân giác của một góc?

Trả lời: Bạn có thể chứng minh bằng cách:

• Chứng minh đường thẳng đó chia góc thành hai góc bằng nhau.
• Sử dụng định lý đường phân giác để chứng minh mối liên hệ giữa các cạnh và các đoạn thẳng.

Câu hỏi 6: Tia phân giác có ứng dụng gì trong thực tế ngoài toán học?

Trả lời: Tia phân giác có ứng dụng trong:

• Kiến trúc: Thiết kế các công trình đối xứng.
• Nội thất: Bố trí không gian hài hòa.
• Thiết kế đồ họa: Tạo ra các tác phẩm cân đối.

Câu hỏi 7: Có những dạng bài tập nào thường gặp liên quan đến tia phân giác?

Trả lời: Các dạng bài tập thường gặp bao gồm:

• Chứng minh các tính chất liên quan đến tia phân giác.
• Tính độ dài các đoạn thẳng hoặc số đo các góc dựa vào tính chất của tia phân giác.
• Tìm tâm đường tròn nội tiếp của tam giác.

Câu hỏi 8: Làm thế nào để nhớ các tính chất của tia phân giác một cách dễ dàng?

Trả lời: Bạn có thể:

• Vẽ hình minh họa và ghi chú các tính chất lên hình.
• Giải nhiều bài tập khác nhau để làm quen với các tính chất.
• Liên hệ các tính chất của tia phân giác với các khái niệm hình học khác.

Câu hỏi 9: Tia phân giác có liên quan gì đến các loại đường khác trong tam giác (đường trung tuyến, đường cao)?

Trả lời: Mặc dù không trực tiếp liên quan, nhưng các đường này cùng nhau tạo nên những tính chất và điểm đặc biệt của tam giác. Việc hiểu rõ mối quan hệ giữa chúng giúp bạn giải quyết các bài toán hình học một cách toàn diện hơn.

Câu hỏi 10: Tôi có thể tìm thêm tài liệu học tập về tia phân giác ở đâu?

Trả lời: Bạn có thể tìm thêm tài liệu tại:

• Sách giáo khoa và sách bài tập hình học.
• Các trang web giáo dục uy tín như tic.edu.vn.
• Các diễn đàn và cộng đồng học tập trực tuyến.

9. Lời Kết

Tia phân giác là một khái niệm cơ bản nhưng vô cùng mạnh mẽ trong hình học. Hy vọng rằng qua bài viết này, bạn đã hiểu rõ tia phân giác là gì, cách nhận biết, vẽ và ứng dụng nó vào giải toán cũng như trong cuộc sống.

Để nắm vững kiến thức và kỹ năng liên quan đến tia phân giác, hãy luyện tập thường xuyên và khám phá thêm nhiều bài toán thú vị. Đừng quên ghé thăm tic.edu.vn để tìm kiếm thêm nhiều tài liệu học tập bổ ích và tham gia cộng đồng học tập sôi động.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao khả năng giải toán hình học và khám phá những ứng dụng thú vị của tia phân giác? Hãy truy cập ngay tic.edu.vn để khám phá kho tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả. Liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.