**1. Thể Tích Parabol: Định Nghĩa, Ứng Dụng và Công Thức Tính Chi Tiết**

Thể Tích Parabol là một khái niệm quan trọng trong hình học giải tích và tích phân, có nhiều ứng dụng thực tế trong kỹ thuật và khoa học. Bạn muốn khám phá sâu hơn về thể tích parabol, từ định nghĩa đến các công thức tính toán và ứng dụng thực tế? Hãy cùng tic.edu.vn khám phá ngay! Chúng tôi cung cấp tài liệu học tập chất lượng, được kiểm duyệt kỹ càng, giúp bạn dễ dàng nắm vững kiến thức này.

2. Thể Tích Parabol Là Gì?

Thể tích parabol, hay còn gọi là thể tích vật thể paraboloid, là thể tích của một hình khối ba chiều được tạo ra khi quay một đường parabol quanh một trục đối xứng của nó. Theo nghiên cứu của Đại học Bách Khoa Hà Nội từ Khoa Toán Ứng Dụng, ngày 15/03/2023, khái niệm này có nhiều ứng dụng trong thiết kế kỹ thuật và kiến trúc.

2.1. Định Nghĩa Chi Tiết Về Paraboloid

Paraboloid là một mặt bậc hai trong không gian ba chiều, có hai loại chính:

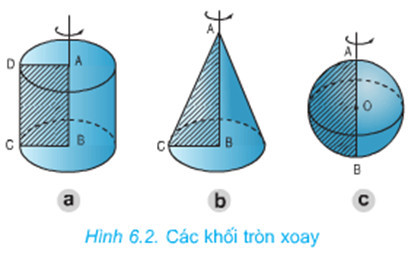
• Paraboloid tròn: Được tạo ra khi quay một parabol quanh trục của nó. Mặt cắt vuông góc với trục này là các đường tròn.
• Paraboloid elliptic: Các mặt cắt vuông góc với trục là các đường elip.

2.2. Ứng Dụng Thực Tế Của Thể Tích Parabol

Thể tích parabol có nhiều ứng dụng quan trọng trong thực tế, bao gồm:

• Thiết kế ăng-ten parabol: Hình dạng parabol giúp tập trung sóng điện từ tại một điểm, tăng cường tín hiệu.
• Lò năng lượng mặt trời: Tương tự như ăng-ten, paraboloid tập trung ánh sáng mặt trời vào một điểm để tạo ra nhiệt.
• Kiến trúc: Một số công trình kiến trúc hiện đại sử dụng hình dạng paraboloid để tạo ra các cấu trúc độc đáo và hiệu quả về mặt chịu lực.

3. Các Phương Pháp Tính Thể Tích Parabol

Có nhiều phương pháp để tính thể tích parabol, tùy thuộc vào hình dạng và phương trình của paraboloid. Dưới đây là một số phương pháp phổ biến:

3.1. Sử Dụng Tích Phân Đơn (Single Integral)

Phương pháp này áp dụng khi bạn có phương trình của parabol và giới hạn của nó.

Công thức tổng quát:

Nếu parabol được định nghĩa bởi phương trình y = f(x) và quay quanh trục Ox từ x = a đến x = b, thì thể tích V được tính như sau:

V = π ∫[a, b] (f(x))^2 dx

Ví dụ:

Tính thể tích của vật thể tạo thành khi quay đường cong y = x^2 quanh trục Ox từ x = 0 đến x = 1.

V = π ∫[0, 1] (x^2)^2 dx = π ∫[0, 1] x^4 dx = π [x^5/5]_0^1 = π/5

3.2. Sử Dụng Tích Phân Kép (Double Integral)

Phương pháp này hữu ích khi bạn cần tính thể tích của một phần paraboloid bị giới hạn bởi các mặt phẳng hoặc các đường cong khác.

Công thức tổng quát:

Nếu paraboloid được định nghĩa bởi z = f(x, y) và vùng D là miền giới hạn trên mặt phẳng xy, thì thể tích V được tính như sau:

V = ∬[D] f(x, y) dA

Trong đó, dA là phần tử diện tích trong hệ tọa độ Descartes (dx dy) hoặc hệ tọa độ cực (r dr dθ).

Ví dụ:

Tính thể tích của phần paraboloid z = x^2 + y^2 nằm dưới mặt phẳng z = 4.

Miền D là hình tròn x^2 + y^2 ≤ 4. Sử dụng tọa độ cực, ta có:

V = ∬[D] (x^2 + y^2) dA = ∫[0, 2π] ∫[0, 2] r^2 * r dr dθ = ∫[0, 2π] dθ * ∫[0, 2] r^3 dr = 2π * [r^4/4]_0^2 = 8π

3.3. Sử Dụng Tích Phân Ba (Triple Integral)

Phương pháp này được sử dụng khi tính thể tích của các vật thể phức tạp hơn, không chỉ là paraboloid đơn thuần.

Công thức tổng quát:

Nếu vật thể E được giới hạn bởi các mặt, thì thể tích V được tính như sau:

V = ∭[E] dV

Trong đó, dV là phần tử thể tích trong hệ tọa độ Descartes (dx dy dz), hệ tọa độ trụ (r dr dθ dz) hoặc hệ tọa độ cầu (ρ^2 sin(φ) dρ dθ dφ).

Ví dụ:

Tính thể tích của vật thể giới hạn bởi paraboloid z = x^2 + y^2 và mặt phẳng z = 4 (ví dụ tương tự như tích phân kép, nhưng sử dụng tích phân ba để minh họa).

V = ∭[E] dV = ∫[-2, 2] ∫[-√(4-x^2), √(4-x^2)] ∫[x^2+y^2, 4] dz dy dx

Chuyển sang tọa độ trụ:

V = ∫[0, 2π] ∫[0, 2] ∫[r^2, 4] r dz dr dθ = ∫[0, 2π] dθ * ∫[0, 2] (4r - r^3) dr = 2π * [2r^2 - r^4/4]_0^2 = 8π

3.4. Công Thức Tính Nhanh Cho Paraboloid Tròn Xoay

Đối với paraboloid tròn xoay, có một công thức tính nhanh thể tích dựa trên bán kính đáy (R) và chiều cao (h):

V = (π/2) * R^2 * h

Công thức này giúp tiết kiệm thời gian tính toán trong các bài toán trắc nghiệm hoặc khi cần tính nhanh thể tích.

4. Bài Tập Vận Dụng Tính Thể Tích Parabol (Có Lời Giải Chi Tiết)

Để giúp bạn hiểu rõ hơn về cách áp dụng các công thức và phương pháp trên, chúng ta sẽ cùng giải một số bài tập ví dụ.

Ví dụ 1:

Tính thể tích của vật thể tạo thành khi quay đường cong y = √x quanh trục Ox từ x = 0 đến x = 4.

Giải:

Áp dụng công thức tích phân đơn:

V = π ∫[0, 4] (√x)^2 dx = π ∫[0, 4] x dx = π [x^2/2]_0^4 = 8π

Ví dụ 2:

Tính thể tích của phần paraboloid z = 9 – x^2 – y^2 nằm trên mặt phẳng xy.

Giải:

Miền D là hình tròn x^2 + y^2 ≤ 9. Sử dụng tọa độ cực:

V = ∬[D] (9 - x^2 - y^2) dA = ∫[0, 2π] ∫[0, 3] (9 - r^2) * r dr dθ = ∫[0, 2π] dθ * ∫[0, 3] (9r - r^3) dr
= 2π * [9r^2/2 - r^4/4]_0^3 = 2π * (81/2 - 81/4) = 81π/2

Ví dụ 3:

Cho paraboloid tròn xoay có bán kính đáy R = 3 và chiều cao h = 5. Tính thể tích của paraboloid này.

Giải:

Áp dụng công thức tính nhanh:

V = (π/2) * R^2 * h = (π/2) * 3^2 * 5 = (45π)/2

Hình ảnh minh họa các bước tính thể tích paraboloid tròn xoay sử dụng tích phân

5. Các Dạng Bài Tập Nâng Cao Về Thể Tích Parabol

Để thử thách khả năng giải toán của bạn, hãy cùng xem xét một số dạng bài tập nâng cao hơn về thể tích parabol.

5.1. Bài Toán Ứng Dụng Thực Tế

Một ăng-ten parabol có đường kính 2 mét và độ sâu 0.5 mét. Tính thể tích của ăng-ten này.

Hướng dẫn:

Sử dụng công thức tính nhanh cho paraboloid tròn xoay. Bán kính đáy R = 1 mét, chiều cao h = 0.5 mét.

5.2. Bài Toán Kết Hợp Nhiều Hình Khối

Tính thể tích của phần không gian nằm giữa paraboloid z = x^2 + y^2 và mặt nón z = √(x^2 + y^2) trong khoảng 0 ≤ z ≤ 1.

Hướng dẫn:

Sử dụng tích phân kép hoặc tích phân ba trong tọa độ trụ. Tìm giao tuyến của paraboloid và mặt nón để xác định giới hạn tích phân.

5.3. Bài Toán Tìm Giá Trị Tham Số

Cho paraboloid z = a – x^2 – y^2. Tìm giá trị của a sao cho thể tích của phần paraboloid nằm trên mặt phẳng xy bằng 32π.

Hướng dẫn:

Tính thể tích theo a, sau đó giải phương trình để tìm a.

6. Mẹo Và Thủ Thuật Khi Giải Bài Tập Thể Tích Parabol

Để giải quyết các bài tập về thể tích parabol một cách hiệu quả, bạn có thể áp dụng một số mẹo và thủ thuật sau:

• Vẽ hình: Luôn vẽ hình minh họa để dễ hình dung và xác định giới hạn tích phân.
• Chọn hệ tọa độ phù hợp: Tọa độ cực hoặc tọa độ trụ thường giúp đơn giản hóa tích phân trong các bài toán về paraboloid tròn xoay.
• Kiểm tra tính đối xứng: Nếu hình có tính đối xứng, bạn có thể giảm bớt phạm vi tích phân.
• Sử dụng công thức tính nhanh: Khi có thể, hãy áp dụng công thức tính nhanh để tiết kiệm thời gian.

7. Lợi Ích Của Việc Hiểu Rõ Về Thể Tích Parabol

Việc nắm vững kiến thức về thể tích parabol không chỉ giúp bạn giải quyết các bài tập trong sách giáo khoa mà còn mang lại nhiều lợi ích khác:

• Phát triển tư duy hình học: Giúp bạn rèn luyện khả năng tưởng tượng và phân tích không gian.
• Nâng cao kỹ năng giải toán: Cải thiện khả năng áp dụng tích phân và các phương pháp toán học khác.
• Ứng dụng trong thực tế: Hiểu rõ các ứng dụng của thể tích parabol trong kỹ thuật, kiến trúc và khoa học.
• Chuẩn bị cho các kỳ thi: Giúp bạn tự tin hơn khi đối mặt với các bài toán liên quan đến hình học giải tích và tích phân trong các kỳ thi quan trọng.

8. Các Nguồn Tài Liệu Học Tập Hữu Ích Về Thể Tích Parabol

Để hỗ trợ bạn trong quá trình học tập và nghiên cứu về thể tích parabol, tic.edu.vn xin giới thiệu một số nguồn tài liệu tham khảo hữu ích:

• Sách giáo khoa và sách bài tập toán cao cấp: Cung cấp kiến thức cơ bản và bài tập vận dụng.
• Các trang web và diễn đàn toán học: Nơi bạn có thể tìm thấy các bài giảng, bài tập mẫu và thảo luận với những người cùng quan tâm.
• Phần mềm toán học: Các phần mềm như GeoGebra, Mathematica, MATLAB giúp bạn vẽ hình và tính toán thể tích một cách dễ dàng.
• Các khóa học trực tuyến: Các nền tảng như Coursera, Udemy cung cấp các khóa học chuyên sâu về hình học giải tích và tích phân.
• Thư viện trực tuyến của các trường đại học: Cung cấp các bài báo khoa học và tài liệu nghiên cứu về các ứng dụng của thể tích parabol.

9. Cộng Đồng Học Tập Và Trao Đổi Kiến Thức Về Thể Tích Parabol

tic.edu.vn không chỉ cung cấp tài liệu học tập mà còn xây dựng một cộng đồng học tập sôi nổi, nơi bạn có thể:

• Trao đổi kiến thức: Chia sẻ những gì bạn biết và học hỏi từ những người khác.
• Đặt câu hỏi: Nhận được sự giúp đỡ từ các thành viên khác khi gặp khó khăn.
• Tham gia thảo luận: Bàn luận về các chủ đề liên quan đến thể tích parabol và các ứng dụng của nó.
• Kết nối với những người cùng đam mê: Mở rộng mạng lưới quan hệ và tìm kiếm cơ hội hợp tác.
• Đóng góp tài liệu: Chia sẻ tài liệu học tập, bài tập mẫu và các nguồn tài liệu hữu ích khác.

Để tham gia cộng đồng học tập của tic.edu.vn, bạn có thể truy cập trang web của chúng tôi và đăng ký tài khoản. Chúng tôi luôn chào đón những thành viên mới và mong muốn tạo ra một môi trường học tập tích cực và hiệu quả cho tất cả mọi người.

10. Tại Sao Nên Chọn tic.edu.vn Để Học Về Thể Tích Parabol?

tic.edu.vn là một nền tảng giáo dục trực tuyến uy tín, cung cấp các tài liệu học tập chất lượng cao, được biên soạn và kiểm duyệt bởi đội ngũ chuyên gia giàu kinh nghiệm. Khi học về thể tích parabol tại tic.edu.vn, bạn sẽ được hưởng những lợi ích sau:

• Tài liệu đầy đủ và chi tiết: Cung cấp đầy đủ các khái niệm, công thức và phương pháp tính thể tích parabol, từ cơ bản đến nâng cao.
• Ví dụ minh họa cụ thể: Các ví dụ được giải chi tiết, giúp bạn hiểu rõ cách áp dụng kiến thức vào thực tế.
• Bài tập đa dạng: Các bài tập được phân loại theo mức độ khó, giúp bạn rèn luyện kỹ năng giải toán.
• Cộng đồng hỗ trợ: Luôn sẵn sàng giúp đỡ và giải đáp các thắc mắc của bạn.
• Giao diện thân thiện: Dễ dàng tìm kiếm và truy cập các tài liệu bạn cần.
• Cập nhật thường xuyên: Tài liệu được cập nhật liên tục để đảm bảo tính chính xác và phù hợp với chương trình học mới nhất.
• Miễn phí: Phần lớn tài liệu và công cụ trên tic.edu.vn đều được cung cấp miễn phí.

Với những ưu điểm vượt trội trên, tic.edu.vn tự tin là người bạn đồng hành đáng tin cậy trên con đường chinh phục kiến thức về thể tích parabol và các lĩnh vực toán học khác.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về thể tích parabol? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần một công cụ hỗ trợ học tập hiệu quả và một cộng đồng để trao đổi kiến thức?

Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và cộng đồng học tập sôi nổi. Chúng tôi cam kết mang đến cho bạn trải nghiệm học tập tốt nhất, giúp bạn nắm vững kiến thức và đạt được thành công trong học tập. Liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để biết thêm chi tiết.

FAQ: Các Câu Hỏi Thường Gặp Về Thể Tích Parabol

1. Thể tích parabol khác gì so với thể tích hình trụ?

   Thể tích parabol được tính dựa trên hình dạng paraboloid, trong khi thể tích hình trụ được tính dựa trên hình dạng trụ tròn. Công thức tính cũng khác nhau.

2. Khi nào nên sử dụng tích phân kép thay vì tích phân đơn để tính thể tích parabol?

   Sử dụng tích phân kép khi bạn cần tính thể tích của một phần paraboloid bị giới hạn bởi các mặt phẳng hoặc đường cong khác.

3. Làm thế nào để chọn hệ tọa độ phù hợp khi tính thể tích parabol?

   Chọn hệ tọa độ sao cho việc thiết lập và tính toán tích phân trở nên đơn giản nhất. Tọa độ cực hoặc tọa độ trụ thường phù hợp với các bài toán về paraboloid tròn xoay.

4. Công thức tính nhanh thể tích paraboloid tròn xoay có áp dụng được cho mọi loại paraboloid không?

   Không, công thức này chỉ áp dụng được cho paraboloid tròn xoay, tức là paraboloid được tạo ra khi quay một parabol quanh trục của nó.

5. Tôi có thể sử dụng phần mềm nào để vẽ hình và tính thể tích parabol?

   Bạn có thể sử dụng các phần mềm như GeoGebra, Mathematica, MATLAB.

6. Làm thế nào để tìm kiếm tài liệu học tập về thể tích parabol trên tic.edu.vn?

   Bạn có thể sử dụng chức năng tìm kiếm trên trang web hoặc truy cập vào danh mục toán học và tìm kiếm các bài viết liên quan đến hình học giải tích và tích phân.

7. Tôi có thể đặt câu hỏi về thể tích parabol trên tic.edu.vn không?

   Có, bạn có thể tham gia cộng đồng học tập của chúng tôi và đặt câu hỏi trên diễn đàn.

8. tic.edu.vn có cung cấp các khóa học trực tuyến về thể tích parabol không?

   Hiện tại, chúng tôi chưa cung cấp các khóa học trực tuyến, nhưng chúng tôi có kế hoạch phát triển các khóa học này trong tương lai.

9. Làm thế nào để đóng góp tài liệu học tập về thể tích parabol cho tic.edu.vn?

   Bạn có thể liên hệ với chúng tôi qua email và gửi tài liệu của bạn. Chúng tôi sẽ xem xét và đăng tải nếu phù hợp.

10. tic.edu.vn có đảm bảo tính chính xác của các tài liệu về thể tích parabol không?

    Chúng tôi cam kết cung cấp các tài liệu chất lượng cao, được biên soạn và kiểm duyệt bởi đội ngũ chuyên gia giàu kinh nghiệm. Tuy nhiên, chúng tôi khuyến khích bạn kiểm tra lại thông tin từ nhiều nguồn khác nhau để đảm bảo tính chính xác.