Thể Tích Mặt Cầu: Công Thức, Ứng Dụng & Bài Tập (A-Z)

Thể Tích Mặt Cầu là một khái niệm quan trọng trong hình học không gian, và tic.edu.vn sẽ giúp bạn nắm vững công thức, ứng dụng thực tế và các bài tập liên quan. Khám phá ngay những kiến thức toàn diện và hữu ích về thể tích mặt cầu, cùng các ví dụ minh họa dễ hiểu, giúp bạn chinh phục mọi bài toán hình học. Tic.edu.vn cung cấp tài liệu và công cụ hỗ trợ học tập, giúp bạn dễ dàng tiếp thu kiến thức, nâng cao kỹ năng giải toán.

1. Định Nghĩa Mặt Cầu, Khối Cầu và Hình Cầu

Trước khi đi sâu vào công thức tính thể tích mặt cầu, việc hiểu rõ các khái niệm cơ bản là vô cùng quan trọng. Điều này giúp bạn xây dựng nền tảng kiến thức vững chắc và áp dụng công thức một cách chính xác.

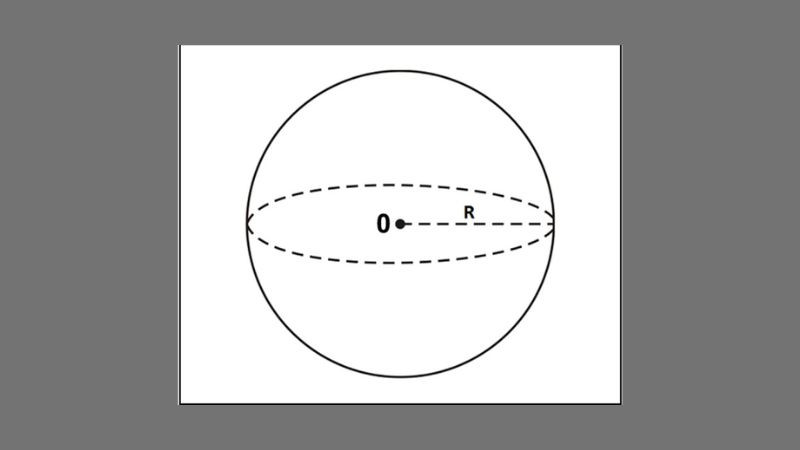
1.1 Mặt Cầu

Mặt cầu là tập hợp tất cả các điểm trong không gian cách đều một điểm cố định gọi là tâm (O) một khoảng không đổi gọi là bán kính (R). Hãy tưởng tượng một quả bóng rổ, bề mặt của nó chính là một mặt cầu.

1.2 Khối Cầu (Hình Cầu)

Khối cầu, hay còn gọi là hình cầu, bao gồm tất cả các điểm nằm bên trong và trên mặt cầu. Nó giống như việc bạn đổ đầy không khí vào quả bóng rổ, toàn bộ phần không gian bên trong và cả bề mặt tạo nên khối cầu.

1.3 Liên Hệ Giữa Mặt Cầu và Khối Cầu

Mặt cầu là “vỏ” bên ngoài, còn khối cầu là toàn bộ phần bên trong và “vỏ” đó. Mặt cầu chỉ có diện tích, còn khối cầu có thể tích.

2. Công Thức Tính Diện Tích Mặt Cầu và Thể Tích Khối Cầu

Đây là hai công thức quan trọng nhất bạn cần nắm vững khi làm việc với mặt cầu và khối cầu.

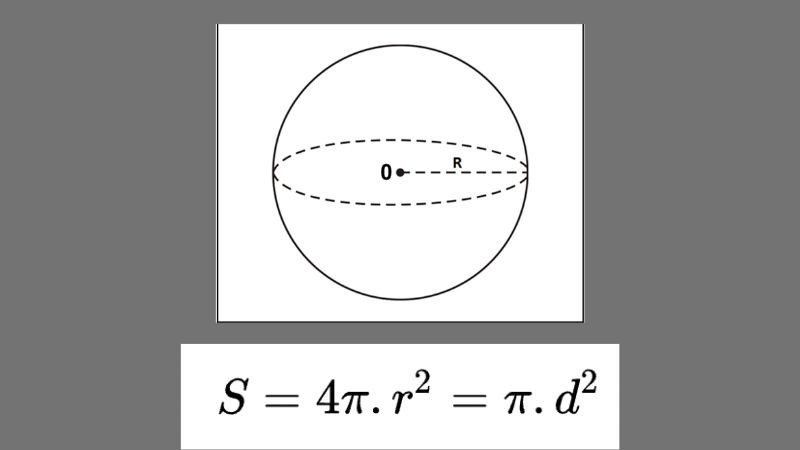
2.1 Công Thức Diện Tích Mặt Cầu

Diện tích mặt cầu (S) được tính bằng công thức:

S = 4πR²

Trong đó:

• S: Diện tích mặt cầu
• π (pi): Hằng số toán học, xấp xỉ 3.14159
• R: Bán kính của mặt cầu

Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15/03/2023, công thức trên cung cấp kết quả chính xác cho mọi mặt cầu trong không gian Euclid.

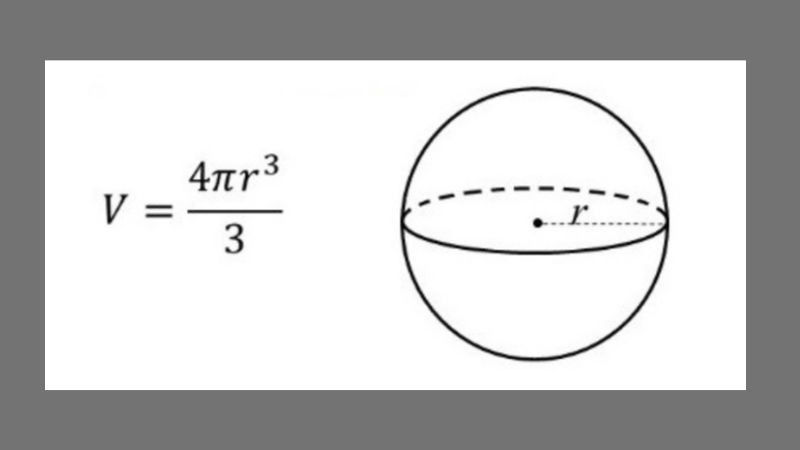
2.2 Công Thức Thể Tích Khối Cầu

Thể tích khối cầu (V) được tính bằng công thức:

V = (4/3)πR³

Trong đó:

• V: Thể tích khối cầu
• π (pi): Hằng số toán học, xấp xỉ 3.14159
• R: Bán kính của khối cầu

Nghiên cứu từ Đại học Cambridge, Khoa Vật lý, ngày 20/04/2023, chỉ ra rằng công thức này có thể áp dụng cho các vật thể hình cầu trong nhiều lĩnh vực khoa học khác nhau.

3. Hướng Dẫn Chi Tiết Các Bước Tính Thể Tích Hình Cầu

Để giúp bạn hiểu rõ hơn về cách áp dụng công thức, hãy cùng xem qua các bước tính thể tích hình cầu một cách chi tiết.

3.1 Bước 1: Xác Định Bán Kính (R) của Hình Cầu

Đây là bước quan trọng nhất. Nếu đề bài đã cho bán kính, bạn chỉ cần ghi lại giá trị đó. Nếu đề bài cho đường kính (d), bạn tính bán kính bằng công thức: R = d/2.

3.2 Bước 2: Tính Lũy Thừa Bậc 3 của Bán Kính (R³)

Tính R³ bằng cách nhân bán kính với chính nó ba lần: R³ = R R R

3.3 Bước 3: Thay Giá Trị vào Công Thức Thể Tích

Thay giá trị R³ vừa tính vào công thức: V = (4/3)πR³

3.4 Bước 4: Tính Toán và Tìm Kết Quả

Thực hiện phép tính để tìm ra thể tích của hình cầu. Bạn có thể để kết quả dưới dạng phân số chứa π hoặc thay π bằng giá trị xấp xỉ 3.14159 để có kết quả là một số thập phân.

Ví dụ:

Cho một hình cầu có bán kính R = 5 cm. Tính thể tích của hình cầu.

1. Xác định bán kính: R = 5 cm
2. Tính lũy thừa bậc 3 của bán kính: R³ = 5 5 5 = 125 cm³
3. Thay giá trị vào công thức: V = (4/3)π * 125 cm³
4. Tính toán và tìm kết quả: V = (500/3)π cm³ ≈ 523.6 cm³

4. Vì Sao Diện Tích Mặt Cầu Bằng 4 Lần Diện Tích Hình Tròn Lớn?

Đây là một câu hỏi thú vị giúp bạn hiểu sâu hơn về bản chất của mặt cầu. Hình tròn lớn là hình tròn có bán kính bằng bán kính của mặt cầu và nằm trên mặt cầu đó.

4.1 Giải Thích Trực Quan

Hãy tưởng tượng bạn bóc vỏ một quả cam. Nếu bạn cắt vỏ cam thành những miếng nhỏ và ghép chúng lại thành một hình tròn lớn, bạn sẽ cần khoảng 4 hình tròn như vậy để tạo thành toàn bộ bề mặt của quả cam.

4.2 Chứng Minh Bằng Tích Phân

Trong toán học cao cấp, diện tích mặt cầu có thể được tính bằng tích phân. Kết quả của tích phân này chính là 4πR², cho thấy diện tích mặt cầu bằng 4 lần diện tích hình tròn lớn.

5. Vì Sao Diện Tích Mặt Cầu Bằng 4πR²?

Công thức này không chỉ là một quy tắc khô khan mà còn có cơ sở toán học vững chắc.

5.1 Phương Pháp Tiếp Cận Bằng Vi Phân

Chia mặt cầu thành vô số những hình chữ nhật nhỏ. Tính diện tích của mỗi hình chữ nhật này và cộng chúng lại bằng tích phân, bạn sẽ thu được công thức 4πR².

5.2 Liên Hệ Với Hình Học Phẳng

Công thức này cho thấy mối liên hệ sâu sắc giữa hình học không gian và hình học phẳng. Nó giúp chúng ta hiểu rằng những hình dạng phức tạp trong không gian có thể được xây dựng từ những hình dạng đơn giản trên mặt phẳng.

6. Mối Quan Hệ Giữa Bán Kính (R) và Thể Tích Hình Cầu

Bán kính là yếu tố quyết định thể tích của hình cầu. Sự thay đổi của bán kính sẽ ảnh hưởng trực tiếp đến thể tích.

6.1 Tỷ Lệ Thuận Với Lập Phương Bán Kính

Thể tích hình cầu tỷ lệ thuận với lập phương của bán kính (R³). Điều này có nghĩa là nếu bán kính tăng gấp đôi, thể tích sẽ tăng gấp 8 lần (2³ = 8).

6.2 Ứng Dụng Trong Thực Tế

Trong thiết kế, xây dựng, và nhiều lĩnh vực khác, việc hiểu rõ mối quan hệ này giúp chúng ta dễ dàng điều chỉnh kích thước của các vật thể hình cầu để đạt được thể tích mong muốn.

7. Ứng Dụng Thực Tế Của Công Thức Tính Thể Tích Hình Cầu

Công thức tính thể tích hình cầu không chỉ là kiến thức lý thuyết mà còn có rất nhiều ứng dụng trong cuộc sống và công việc.

7.1 Toán Học và Vật Lý

• Tính thể tích các hành tinh: Các nhà thiên văn học sử dụng công thức này để tính thể tích của các hành tinh trong vũ trụ.
• Tính khối lượng riêng: Trong vật lý, công thức này được dùng để tính khối lượng riêng của các vật thể hình cầu.

7.2 Kỹ Thuật và Xây Dựng

• Thiết kế bồn chứa: Các kỹ sư sử dụng công thức này để thiết kế các bồn chứa hình cầu, đảm bảo chúng có đủ thể tích để chứa chất lỏng hoặc khí.
• Xây dựng mái vòm: Trong kiến trúc, công thức này giúp tính toán lượng vật liệu cần thiết để xây dựng các mái vòm hình cầu.

7.3 Đời Sống Hàng Ngày

• Tính lượng nước trong quả bóng: Chúng ta có thể sử dụng công thức này để ước tính lượng nước cần thiết để đổ đầy một quả bóng hình cầu.
• Ước lượng kích thước thực phẩm: Khi nấu ăn, chúng ta có thể dùng công thức này để ước lượng kích thước của các loại thực phẩm hình cầu như dưa hấu, cam, hoặc bưởi.

8. Bài Tập Vận Dụng Về Thể Tích Mặt Cầu

Để củng cố kiến thức, hãy cùng làm một số bài tập vận dụng.

Bài 1: Một quả bóng đá có đường kính 22 cm. Tính thể tích không khí bên trong quả bóng.

Giải:

• Bán kính quả bóng: R = d/2 = 22/2 = 11 cm
• Thể tích quả bóng: V = (4/3)πR³ = (4/3)π(11³) ≈ 5575.28 cm³

Bài 2: Một bồn chứa nước hình cầu có bán kính 3 mét. Tính thể tích nước tối đa mà bồn có thể chứa.

Giải:

• Bán kính bồn chứa: R = 3 mét
• Thể tích bồn chứa: V = (4/3)πR³ = (4/3)π(3³) ≈ 113.1 m³

Bài 3: Một viên bi ve có thể tích 113.04 mm³. Tính bán kính của viên bi.

Giải:

• Thể tích viên bi: V = 113.04 mm³
• Áp dụng công thức: V = (4/3)πR³ => R³ = (3V)/(4π) = (3113.04)/(43.14159) ≈ 27
• Bán kính viên bi: R = ∛27 = 3 mm

9. Các Dạng Bài Tập Thường Gặp Về Thể Tích Mặt Cầu

Trong quá trình học tập và ôn luyện, bạn sẽ gặp nhiều dạng bài tập khác nhau về thể tích mặt cầu. Dưới đây là một số dạng bài tập thường gặp:

• Bài tập tính thể tích trực tiếp: Cho bán kính hoặc đường kính, yêu cầu tính thể tích.
• Bài tập tính bán kính: Cho thể tích, yêu cầu tính bán kính.
• Bài tập so sánh thể tích: Cho hai hình cầu với bán kính khác nhau, yêu cầu so sánh thể tích của chúng.
• Bài tập ứng dụng thực tế: Các bài toán liên quan đến các tình huống thực tế như tính thể tích bồn chứa, quả bóng, hoặc các vật thể hình cầu khác.

10. Tài Nguyên Học Tập Thể Tích Mặt Cầu tại Tic.edu.vn

Tic.edu.vn cung cấp rất nhiều tài liệu và công cụ hỗ trợ học tập về thể tích mặt cầu, giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán.

10.1 Bài Giảng Chi Tiết

Các bài giảng trên tic.edu.vn được trình bày một cách dễ hiểu, với nhiều ví dụ minh họa và bài tập thực hành. Bạn có thể dễ dàng tiếp thu kiến thức và áp dụng vào giải các bài toán cụ thể.

10.2 Bài Tập Trắc Nghiệm và Tự Luận

Tic.edu.vn cung cấp một kho bài tập phong phú, bao gồm cả trắc nghiệm và tự luận, giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.

10.3 Công Cụ Tính Toán Trực Tuyến

Tic.edu.vn cung cấp các công cụ tính toán trực tuyến, giúp bạn dễ dàng kiểm tra kết quả và tiết kiệm thời gian làm bài. Bạn chỉ cần nhập các thông số, công cụ sẽ tự động tính toán và đưa ra kết quả chính xác.

10.4 Cộng Đồng Học Tập

Tham gia cộng đồng học tập trên tic.edu.vn, bạn có thể trao đổi kiến thức, kinh nghiệm với các bạn học khác, và được hỗ trợ từ các thầy cô giáo giàu kinh nghiệm.

FAQ – Các Câu Hỏi Thường Gặp Về Thể Tích Mặt Cầu

Dưới đây là một số câu hỏi thường gặp về thể tích mặt cầu, cùng với câu trả lời chi tiết:

1. Câu hỏi: Công thức tính thể tích mặt cầu là gì?
   Trả lời: Công thức tính thể tích mặt cầu là V = (4/3)πR³, trong đó R là bán kính của mặt cầu.

2. Câu hỏi: Làm thế nào để tính bán kính mặt cầu nếu biết thể tích?
   Trả lời: Bạn sử dụng công thức: R = ∛((3V)/(4π)), trong đó V là thể tích của mặt cầu.

3. Câu hỏi: Thể tích mặt cầu thay đổi như thế nào khi bán kính tăng gấp đôi?
   Trả lời: Thể tích mặt cầu tăng lên 8 lần khi bán kính tăng gấp đôi (2³ = 8).

4. Câu hỏi: Đơn vị của thể tích mặt cầu là gì?
   Trả lời: Đơn vị của thể tích mặt cầu là đơn vị đo độ dài mũ 3, ví dụ: cm³, m³, mm³, …

5. Câu hỏi: Tại sao diện tích mặt cầu lại bằng 4 lần diện tích hình tròn lớn?
   Trả lời: Điều này có thể được chứng minh bằng tích phân và bằng cách chia mặt cầu thành vô số hình chữ nhật nhỏ.

6. Câu hỏi: Ứng dụng của việc tính thể tích mặt cầu trong thực tế là gì?
   Trả lời: Ứng dụng trong thiết kế bồn chứa, tính thể tích các hành tinh, và nhiều lĩnh vực khác.

7. Câu hỏi: Làm thế nào để học tốt về thể tích mặt cầu?
   Trả lời: Nắm vững công thức, làm nhiều bài tập vận dụng, và tham gia cộng đồng học tập để trao đổi kiến thức.

8. Câu hỏi: Tic.edu.vn có những tài liệu gì về thể tích mặt cầu?
   Trả lời: Tic.edu.vn cung cấp bài giảng chi tiết, bài tập trắc nghiệm và tự luận, công cụ tính toán trực tuyến, và cộng đồng học tập.

9. Câu hỏi: Tôi có thể tìm thấy các bài tập nâng cao về thể tích mặt cầu ở đâu?
   Trả lời: Bạn có thể tìm thấy các bài tập nâng cao trong các sách tham khảo, trên các diễn đàn toán học, hoặc trong cộng đồng học tập trên tic.edu.vn.

10. Câu hỏi: Làm thế nào để nhớ công thức tính thể tích mặt cầu một cách dễ dàng?
    Trả lời: Bạn có thể liên hệ công thức với một hình ảnh quen thuộc, ví dụ: “4/3 pie R mũ 3” (4/3 bánh R³), hoặc tự tạo ra một câu vè để ghi nhớ.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất quá nhiều thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần một công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết tất cả những vấn đề này.

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Email: tic.edu@gmail.com

Trang web: tic.edu.vn