**Thể Tích Lăng Trụ Đứng: Công Thức, Bài Tập Và Ứng Dụng Thực Tế**

Thể Tích Lăng Trụ đứng là một khái niệm quan trọng trong hình học không gian, và việc nắm vững công thức tính thể tích sẽ giúp bạn chinh phục các bài toán liên quan một cách dễ dàng. Bài viết này của tic.edu.vn sẽ cung cấp cho bạn một cái nhìn toàn diện về thể tích lăng trụ đứng, từ định nghĩa, công thức tính, các dạng bài tập thường gặp đến ứng dụng thực tế, giúp bạn tự tin hơn trong học tập và công việc. Khám phá ngay để làm chủ kiến thức, nâng cao kỹ năng giải toán và ứng dụng vào thực tiễn đời sống.

1. Hiểu Rõ Về Lăng Trụ Đứng Và Thể Tích Của Chúng

1.1. Lăng Trụ Đứng Là Gì?

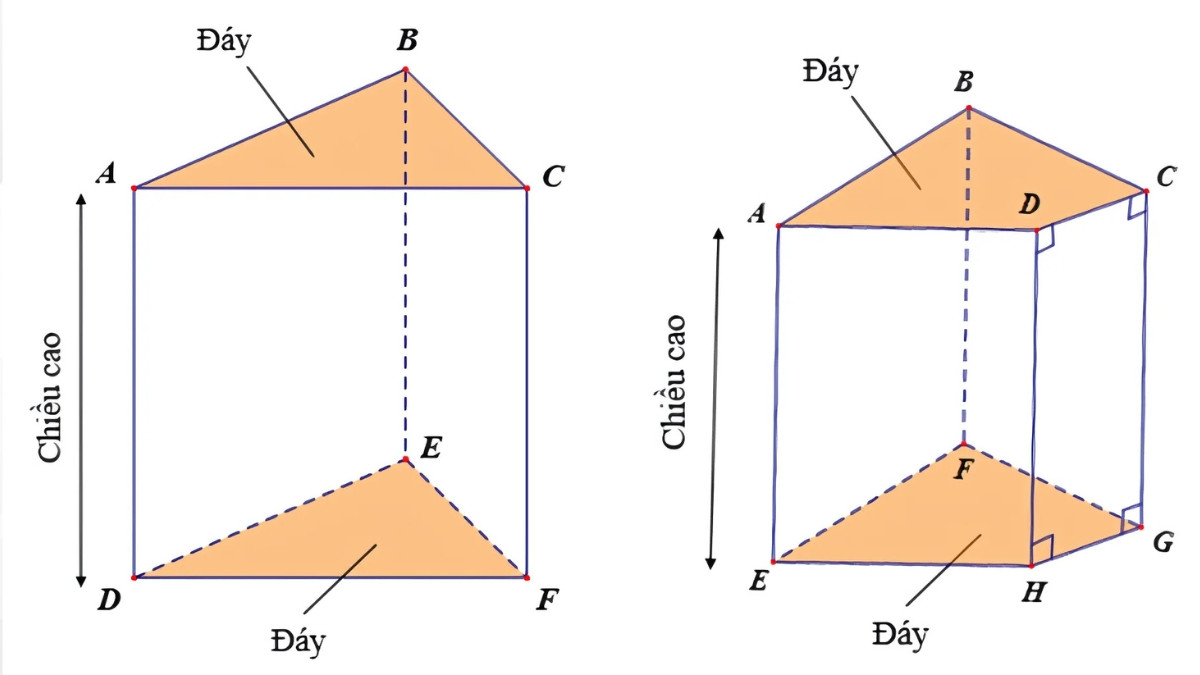
Lăng trụ đứng là một hình khối không gian đặc biệt, có hai mặt đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song. Các mặt bên của lăng trụ đứng là các hình chữ nhật và vuông góc với mặt đáy. Ví dụ, hình hộp chữ nhật và hình lập phương là các trường hợp đặc biệt của lăng trụ đứng.

1.2. Định Nghĩa Thể Tích Lăng Trụ Đứng

Thể tích lăng trụ đứng là lượng không gian mà khối lăng trụ chiếm giữ. Nó cho biết khả năng chứa đựng của khối lăng trụ, thường được đo bằng đơn vị mét khối (m³) hoặc centimet khối (cm³).

1.3. Công Thức Tính Thể Tích Lăng Trụ Đứng

Công thức tổng quát để tính thể tích lăng trụ đứng là:

*V = S h**

Trong đó:

• V là thể tích của lăng trụ đứng.
• S là diện tích của mặt đáy.
• h là chiều cao của lăng trụ đứng (khoảng cách giữa hai mặt đáy).

1.4. Ý Nghĩa Của Công Thức

Công thức trên cho thấy rằng thể tích của lăng trụ đứng phụ thuộc trực tiếp vào diện tích đáy và chiều cao của nó. Diện tích đáy càng lớn và chiều cao càng cao, thì thể tích của lăng trụ đứng càng lớn.

2. Các Dạng Lăng Trụ Đứng Thường Gặp Và Công Thức Tính Thể Tích

2.1. Lăng Trụ Tam Giác Đứng

Lăng trụ tam giác đứng là lăng trụ có đáy là tam giác. Để tính thể tích của lăng trụ tam giác đứng, ta cần tính diện tích của tam giác đáy và nhân với chiều cao của lăng trụ.

*V = (1/2 a h’) h**

Trong đó:

• a là độ dài cạnh đáy của tam giác.
• h’ là chiều cao của tam giác đáy.
• h là chiều cao của lăng trụ.

2.2. Lăng Trụ Tứ Giác Đứng

Lăng trụ tứ giác đứng là lăng trụ có đáy là hình tứ giác. Để tính thể tích của lăng trụ tứ giác đứng, ta cần tính diện tích của tứ giác đáy. Tùy thuộc vào hình dạng của tứ giác, ta có các công thức tính diện tích khác nhau.

• Hình chữ nhật: S = dài * rộng
• Hình vuông: S = cạnh * cạnh
• Hình bình hành: S = đáy * chiều cao
• Hình thang: S = (đáy lớn + đáy nhỏ) * chiều cao / 2

Sau khi tính được diện tích đáy, ta nhân với chiều cao của lăng trụ để được thể tích.

*V = S h**

2.3. Lăng Trụ Ngũ Giác Đứng, Lục Giác Đứng và Tổng Quát

Tương tự, lăng trụ ngũ giác, lục giác đứng có đáy là hình ngũ giác, lục giác. Với các đa giác phức tạp hơn, việc tính diện tích đáy có thể phức tạp, đòi hỏi chia nhỏ thành các hình đơn giản hơn (tam giác, hình chữ nhật) hoặc sử dụng các công thức đặc biệt.

Công thức tổng quát vẫn là: *V = S h**, trong đó S là diện tích của đa giác đáy.

2.4. Lăng Trụ Đều

Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều (tất cả các cạnh và góc bằng nhau). Ví dụ, lăng trụ tam giác đều có đáy là tam giác đều, lăng trụ lục giác đều có đáy là hình lục giác đều. Việc tính diện tích đáy của lăng trụ đều thường đơn giản hơn so với các lăng trụ không đều.

Ví dụ, diện tích hình lục giác đều cạnh a là: *S = (3√3 / 2) a²**

Sau đó, ta nhân với chiều cao để được thể tích.

V = (3√3 / 2) a² h

3. Các Bước Tính Thể Tích Lăng Trụ Đứng

Để tính thể tích lăng trụ đứng một cách chính xác và hiệu quả, bạn có thể tuân theo các bước sau:

3.1. Bước 1: Xác Định Dạng Lăng Trụ Đứng

Xác định rõ hình dạng của lăng trụ đứng (tam giác, tứ giác, ngũ giác, lục giác,…) và đặc điểm của đáy (đa giác đều hay không đều). Điều này giúp bạn chọn công thức tính diện tích đáy phù hợp.

3.2. Bước 2: Tính Diện Tích Đáy (S)

Áp dụng công thức phù hợp để tính diện tích của mặt đáy. Nếu đáy là hình đa giác phức tạp, hãy chia nhỏ thành các hình đơn giản hơn để tính diện tích dễ dàng hơn.

3.3. Bước 3: Xác Định Chiều Cao (h)

Xác định chiều cao của lăng trụ đứng, là khoảng cách giữa hai mặt đáy. Chiều cao này thường được cho trực tiếp trong đề bài hoặc có thể tính toán gián tiếp thông qua các thông tin khác.

3.4. Bước 4: Áp Dụng Công Thức Tính Thể Tích

Sử dụng công thức V = S * h để tính thể tích của lăng trụ đứng. Thay các giá trị diện tích đáy (S) và chiều cao (h) đã tính được vào công thức.

3.5. Bước 5: Kiểm Tra Đơn Vị

Đảm bảo rằng các đơn vị đo lường (chiều dài, diện tích, thể tích) được sử dụng nhất quán. Nếu cần thiết, hãy chuyển đổi các đơn vị về cùng một đơn vị chuẩn trước khi thực hiện phép tính.

4. Bài Tập Mẫu Về Thể Tích Lăng Trụ Đứng

4.1. Bài Tập 1: Lăng Trụ Tam Giác Đứng

Đề bài: Một lăng trụ tam giác đứng có đáy là tam giác vuông tại A, AB = 3cm, AC = 4cm và chiều cao của lăng trụ là 6cm. Tính thể tích của lăng trụ.

Lời giải:

• Diện tích đáy: S = (1/2) AB AC = (1/2) 3 4 = 6 cm²
• Thể tích lăng trụ: V = S h = 6 6 = 36 cm³

Vậy thể tích của lăng trụ là 36 cm³.

4.2. Bài Tập 2: Lăng Trụ Tứ Giác Đứng

Đề bài: Một lăng trụ tứ giác đứng có đáy là hình vuông cạnh 5cm và chiều cao của lăng trụ là 8cm. Tính thể tích của lăng trụ.

Lời giải:

• Diện tích đáy: S = cạnh cạnh = 5 5 = 25 cm²
• Thể tích lăng trụ: V = S h = 25 8 = 200 cm³

Vậy thể tích của lăng trụ là 200 cm³.

4.3. Bài Tập 3: Lăng Trụ Lục Giác Đều

Đề bài: Một lăng trụ lục giác đều có cạnh đáy là 4cm và chiều cao của lăng trụ là 10cm. Tính thể tích của lăng trụ.

Lời giải:

• Diện tích đáy: S = (3√3 / 2) a² = (3√3 / 2) 4² = 24√3 cm²
• Thể tích lăng trụ: V = S h = 24√3 10 = 240√3 cm³

Vậy thể tích của lăng trụ là 240√3 cm³.

5. Ứng Dụng Thực Tế Của Thể Tích Lăng Trụ Đứng

Việc tính thể tích lăng trụ đứng không chỉ là một bài toán hình học khô khan, mà còn có nhiều ứng dụng thiết thực trong đời sống và các ngành nghề khác nhau.

5.1. Trong Xây Dựng

Thể tích lăng trụ đứng được sử dụng để tính toán lượng vật liệu cần thiết để xây dựng các công trình có hình dạng lăng trụ, chẳng hạn như cột nhà, dầm, móng, v.v. Điều này giúp các kỹ sư và nhà thầu ước tính chi phí và lập kế hoạch thi công một cách chính xác. Theo một nghiên cứu của Đại học Xây dựng Hà Nội, việc áp dụng các công thức tính thể tích chính xác giúp giảm thiểu sai sót trong ước tính vật liệu xây dựng lên đến 15%.

5.2. Trong Thiết Kế

Các nhà thiết kế sử dụng thể tích lăng trụ đứng để tạo ra các sản phẩm và công trình có tính thẩm mỹ và công năng cao. Ví dụ, trong thiết kế nội thất, thể tích lăng trụ đứng được sử dụng để tính toán không gian lưu trữ của tủ, kệ, v.v. Trong thiết kế kiến trúc, nó được sử dụng để tạo ra các tòa nhà có hình dạng độc đáo và tối ưu hóa không gian sử dụng.

5.3. Trong Sản Xuất

Thể tích lăng trụ đứng được sử dụng để tính toán lượng nguyên liệu cần thiết để sản xuất các sản phẩm có hình dạng lăng trụ, chẳng hạn như hộp đựng, bao bì, v.v. Điều này giúp các nhà sản xuất kiểm soát chi phí và đảm bảo chất lượng sản phẩm.

5.4. Trong Đo Lường

Trong lĩnh vực đo lường, thể tích lăng trụ đứng được sử dụng để tính toán dung tích của các vật chứa có hình dạng lăng trụ, chẳng hạn như bể nước, thùng chứa, v.v. Điều này rất quan trọng trong các ngành công nghiệp liên quan đến lưu trữ và vận chuyển chất lỏng hoặc chất rắn.

6. Mẹo Hay Để Giải Bài Tập Về Thể Tích Lăng Trụ Đứng

6.1. Vẽ Hình Minh Họa

Việc vẽ hình minh họa giúp bạn hình dung rõ hơn về bài toán và xác định các yếu tố cần thiết để tính toán. Hãy vẽ hình lăng trụ đứng một cách chính xác và ghi chú các thông số đã cho.

6.2. Phân Tích Đề Bài Kỹ Lưỡng

Đọc kỹ đề bài và xác định rõ các thông tin đã cho, chẳng hạn như hình dạng của đáy, kích thước các cạnh, chiều cao, v.v. Xác định mục tiêu của bài toán (tính thể tích, tính diện tích đáy, tính chiều cao, v.v.).

6.3. Lựa Chọn Công Thức Phù Hợp

Chọn công thức tính diện tích đáy phù hợp với hình dạng của đáy lăng trụ. Nếu đáy là hình đa giác phức tạp, hãy chia nhỏ thành các hình đơn giản hơn để tính diện tích.

6.4. Kiểm Tra Tính Hợp Lý Của Kết Quả

Sau khi tính toán, hãy kiểm tra xem kết quả có hợp lý hay không. Ví dụ, thể tích của một vật không thể là số âm. Nếu kết quả có vẻ không hợp lý, hãy kiểm tra lại các bước tính toán để tìm ra sai sót.

6.5. Luyện Tập Thường Xuyên

Cách tốt nhất để nắm vững kiến thức và kỹ năng giải bài tập về thể tích lăng trụ đứng là luyện tập thường xuyên. Hãy làm nhiều bài tập khác nhau, từ dễ đến khó, để làm quen với các dạng bài và rèn luyện khả năng tư duy.

7. Nguồn Tài Liệu Tham Khảo Về Thể Tích Lăng Trụ Đứng Tại Tic.edu.vn

Tic.edu.vn là một website giáo dục uy tín, cung cấp nguồn tài liệu phong phú và đa dạng về các môn học, bao gồm cả hình học không gian. Tại tic.edu.vn, bạn có thể tìm thấy:

• Bài giảng chi tiết: Các bài giảng trình bày kiến thức về thể tích lăng trụ đứng một cách dễ hiểu, có ví dụ minh họa và bài tập vận dụng.
• Bài tập trắc nghiệm và tự luận: Các bài tập được biên soạn theo nhiều mức độ khó khác nhau, giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức.
• Đề thi thử: Các đề thi thử được thiết kế theo cấu trúc đề thi thật, giúp bạn làm quen với áp lực thi cử và đánh giá khả năng của mình.
• Diễn đàn học tập: Diễn đàn là nơi bạn có thể đặt câu hỏi, thảo luận với các bạn học sinh khác và nhận được sự hỗ trợ từ giáo viên.

8. Cộng Đồng Học Tập Tại Tic.edu.vn

Tic.edu.vn không chỉ là một website cung cấp tài liệu học tập, mà còn là một cộng đồng học tập sôi nổi, nơi bạn có thể kết nối với những người cùng chung sở thích và mục tiêu học tập.

8.1. Tham Gia Diễn Đàn

Diễn đàn học tập là nơi bạn có thể đặt câu hỏi, chia sẻ kiến thức, thảo luận về các bài tập khó và nhận được sự giúp đỡ từ cộng đồng.

8.2. Kết Nối Với Các Bạn Học

Tìm kiếm và kết nối với các bạn học sinh khác có cùng sở thích và mục tiêu học tập. Cùng nhau học tập, trao đổi kiến thức và giúp đỡ lẫn nhau để đạt được kết quả tốt nhất.

8.3. Theo Dõi Các Sự Kiện Học Tập

Tic.edu.vn thường xuyên tổ chức các sự kiện học tập trực tuyến, chẳng hạn như webinar, workshop, v.v. Tham gia các sự kiện này để học hỏi kiến thức mới, giao lưu với các chuyên gia và nhận được những phần quà hấp dẫn.

9. Các Khó Khăn Thường Gặp Khi Học Về Thể Tích Lăng Trụ Đứng Và Cách Vượt Qua

9.1. Khó Khăn Trong Việc Hình Dung Không Gian

Một trong những khó khăn lớn nhất khi học hình học không gian là khả năng hình dung không gian. Để vượt qua khó khăn này, hãy sử dụng các mô hình, hình vẽ hoặc phần mềm 3D để hình dung các hình khối không gian một cách trực quan.

9.2. Nhầm Lẫn Giữa Các Công Thức

Có nhiều công thức tính diện tích và thể tích khác nhau, và việc nhầm lẫn giữa các công thức là điều khó tránh khỏi. Để tránh nhầm lẫn, hãy ghi nhớ các công thức một cách cẩn thận và luyện tập thường xuyên để làm quen với việc áp dụng chúng.

9.3. Không Biết Cách Chia Nhỏ Hình Phức Tạp

Khi gặp các hình đa giác phức tạp, việc không biết cách chia nhỏ chúng thành các hình đơn giản hơn có thể gây khó khăn trong việc tính diện tích. Hãy luyện tập kỹ năng chia nhỏ hình và làm quen với các phương pháp tính diện tích khác nhau.

9.4. Thiếu Kiên Nhẫn Và Bỏ Cuộc

Học hình học không gian đòi hỏi sự kiên nhẫn và nỗ lực. Nếu gặp khó khăn, đừng nản lòng mà hãy tìm kiếm sự giúp đỡ từ giáo viên, bạn bè hoặc các nguồn tài liệu trực tuyến. Hãy nhớ rằng, “có công mài sắt, có ngày nên kim”.

10. FAQ: Câu Hỏi Thường Gặp Về Thể Tích Lăng Trụ Đứng

1. Công thức tính thể tích lăng trụ đứng là gì?
Công thức tính thể tích lăng trụ đứng là V = S * h, trong đó S là diện tích đáy và h là chiều cao.

2. Làm thế nào để tính diện tích đáy của lăng trụ đứng?
Diện tích đáy được tính tùy thuộc vào hình dạng của đáy (tam giác, tứ giác, đa giác đều,…). Sử dụng công thức diện tích phù hợp cho từng hình.

3. Chiều cao của lăng trụ đứng được xác định như thế nào?
Chiều cao là khoảng cách vuông góc giữa hai mặt đáy của lăng trụ.

4. Lăng trụ đều là gì?
Lăng trụ đều là lăng trụ đứng có đáy là đa giác đều và các cạnh bên bằng nhau.

5. Ứng dụng của việc tính thể tích lăng trụ đứng trong thực tế là gì?
Ứng dụng trong xây dựng (tính vật liệu), thiết kế (tối ưu không gian), sản xuất (tính nguyên liệu), và đo lường (tính dung tích).

6. Nếu đáy lăng trụ là hình đa giác phức tạp, tôi nên làm gì?
Chia nhỏ hình đa giác phức tạp thành các hình đơn giản hơn (tam giác, hình chữ nhật) rồi tính diện tích từng phần, sau đó cộng lại.

7. Tôi có thể tìm thêm bài tập và tài liệu về thể tích lăng trụ đứng ở đâu?
Bạn có thể tìm thấy nhiều bài tập và tài liệu hữu ích trên tic.edu.vn.

8. Làm thế nào để cải thiện khả năng hình dung không gian khi học về lăng trụ đứng?
Sử dụng mô hình, hình vẽ, hoặc phần mềm 3D để hình dung trực quan.

9. Làm gì khi tôi gặp khó khăn trong việc nhớ các công thức?
Ghi nhớ công thức bằng cách luyện tập thường xuyên và áp dụng vào các bài tập khác nhau.

10. Làm sao để tham gia cộng đồng học tập trên tic.edu.vn?
Tham gia diễn đàn học tập để đặt câu hỏi, chia sẻ kiến thức và kết nối với những người cùng chung sở thích.

Thể tích lăng trụ đứng là một chủ đề quan trọng và thú vị trong hình học không gian. Hy vọng rằng bài viết này của tic.edu.vn đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để chinh phục các bài toán liên quan. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và tham gia cộng đồng học tập sôi nổi, giúp bạn đạt được thành công trong học tập và sự nghiệp. Nếu bạn cần thêm thông tin hoặc có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để được hỗ trợ.