Tập Xác Định Hàm Mũ: Bí Quyết Chinh Phục Mọi Bài Toán

admin

2 tháng trước

Tập Xác định Hàm Mũ là kiến thức quan trọng trong chương trình toán học phổ thông, mở ra cánh cửa khám phá thế giới hàm số. Tic.edu.vn sẽ đồng hành cùng bạn, trang bị đầy đủ kiến thức và công cụ để bạn tự tin chinh phục mọi bài toán liên quan đến tập xác định của hàm mũ.

1. Tổng Quan Về Hàm Số Mũ

1.1. Định Nghĩa Hàm Số Mũ

Hàm số mũ là một khái niệm then chốt trong toán học, thường gặp trong chương trình học phổ thông và ứng dụng rộng rãi trong nhiều lĩnh vực khoa học kỹ thuật. Về bản chất, hàm số mũ là hàm số mà trong đó biến số xuất hiện ở vị trí số mũ.

Theo định nghĩa chính thức, hàm số mũ là hàm số có dạng:

y = f(x) = a^x

Trong đó:

a là một số thực dương, khác 1, được gọi là cơ số của hàm số mũ. Điều kiện a > 0 đảm bảo rằng hàm số mũ luôn có giá trị thực. Điều kiện a ≠ 1 giúp phân biệt hàm số mũ với hàm hằng.
x là biến số thực.

Ví dụ về hàm số mũ:

y = 2^x
y = (1/3)^x
y = 10^x

Ví dụ không phải là hàm số mũ:

y = x^2 (Đây là hàm số lũy thừa)
y = 1^x (Đây là hàm hằng)
y = (-2)^x (Không phải hàm số mũ vì cơ số âm)

Ứng dụng của hàm số mũ:

Hàm số mũ không chỉ là một khái niệm toán học trừu tượng mà còn có rất nhiều ứng dụng thực tế trong cuộc sống và khoa học, bao gồm:

Tăng trưởng dân số: Hàm số mũ được sử dụng để mô hình hóa sự tăng trưởng dân số theo thời gian.
Phân rã phóng xạ: Hàm số mũ mô tả quá trình phân rã của các chất phóng xạ.
Lãi kép: Tính lãi kép trong tài chính ngân hàng.
Vật lý: Mô tả các hiện tượng như sự suy giảm ánh sáng khi đi qua môi trường hấp thụ.
Sinh học: Mô hình hóa sự phát triển của vi khuẩn.
Kinh tế: Dự báo tăng trưởng kinh tế.

Theo một nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, hàm số mũ cung cấp một công cụ mạnh mẽ để mô tả và dự đoán nhiều hiện tượng trong thế giới thực.

1.2. Đạo Hàm Của Hàm Số Mũ

Đạo hàm của hàm số mũ là một công cụ quan trọng để khảo sát sự biến thiên và tìm cực trị của hàm số. Công thức đạo hàm của hàm số mũ như sau:

Cho hàm số y = a^x, với a > 0 và a ≠ 1, đạo hàm của hàm số là:

y' = a^x * ln(a)

Trong đó:

y' là đạo hàm của hàm số y theo biến x.
ln(a) là logarit tự nhiên của cơ số a.

Ví dụ:

Cho hàm số y = 2^x, đạo hàm của hàm số là y' = 2^x * ln(2).
Cho hàm số y = e^x, đạo hàm của hàm số là y' = e^x * ln(e) = e^x (vì ln(e) = 1).

Tổng quát hơn:

Cho hàm số y = a^(u(x)), trong đó u(x) là một hàm số theo biến x. Đạo hàm của hàm số là:

y' = a^(u(x)) * ln(a) * u'(x)

Trong đó:

u'(x) là đạo hàm của hàm số u(x) theo biến x.

Ví dụ:

Cho hàm số y = 2^(x^2), đạo hàm của hàm số là y' = 2^(x^2) * ln(2) * 2x.

Ứng dụng của đạo hàm hàm số mũ:

Tìm cực trị của hàm số: Đạo hàm giúp xác định các điểm cực đại và cực tiểu của hàm số, từ đó khảo sát được sự biến thiên của hàm số.
Xác định tính đơn điệu của hàm số: Dựa vào dấu của đạo hàm, ta có thể biết hàm số đồng biến hay nghịch biến trên một khoảng nào đó.
Giải các bài toán liên quan đến tốc độ thay đổi: Đạo hàm biểu thị tốc độ thay đổi của hàm số tại một điểm, có ứng dụng trong các bài toán vật lý, kinh tế.

1.3. Tính Chất Của Hàm Số Mũ

Hàm số mũ có những tính chất đặc trưng, giúp ta hiểu rõ hơn về đồ thị và ứng xử của chúng:

Tính Chất	Mô Tả
Tập xác định	`D = R` (Tập hợp tất cả các số thực)
Tập giá trị	`T = (0; +∞)` (Tập hợp tất cả các số thực dương)
Đạo hàm	`y' = a^x * ln(a)`
Chiều biến thiên	Nếu `a > 1`: Hàm số đồng biến trên `R`. Nếu `0 < a < 1`: Hàm số nghịch biến trên `R`.
Tiệm cận	Trục Ox là tiệm cận ngang của đồ thị hàm số.
Đồ thị	Luôn đi qua điểm (0; 1) và (1; a). Nằm phía trên trục hoành (y = a^x > 0 với mọi x thuộc R).

Giải thích chi tiết:

Tập xác định: Hàm số mũ y = a^x xác định với mọi giá trị thực của x. Điều này có nghĩa là bạn có thể thay bất kỳ số thực nào vào vị trí của x và luôn nhận được một giá trị y tương ứng.
Tập giá trị: Giá trị của hàm số mũ y = a^x luôn dương với mọi giá trị thực của x. Điều này có nghĩa là đồ thị của hàm số mũ luôn nằm phía trên trục hoành.
Đạo hàm: Đạo hàm của hàm số mũ y = a^x là y' = a^x * ln(a). Đạo hàm này cho biết tốc độ thay đổi của hàm số tại một điểm.
Chiều biến thiên:
- Nếu a > 1, hàm số mũ đồng biến trên R. Điều này có nghĩa là khi x tăng, y cũng tăng. Đồ thị của hàm số dốc lên từ trái sang phải.
- Nếu 0 < a < 1, hàm số mũ nghịch biến trên R. Điều này có nghĩa là khi x tăng, y giảm. Đồ thị của hàm số dốc xuống từ trái sang phải.
Tiệm cận: Trục Ox (đường thẳng y = 0) là tiệm cận ngang của đồ thị hàm số mũ. Điều này có nghĩa là khi x tiến tới vô cùng (dương hoặc âm), giá trị của y tiến gần đến 0, nhưng không bao giờ chạm vào trục Ox.
Đồ thị:
- Đồ thị của hàm số mũ luôn đi qua điểm (0; 1). Điều này có nghĩa là khi x = 0, y = a^0 = 1.
- Đồ thị của hàm số mũ luôn đi qua điểm (1; a). Điều này có nghĩa là khi x = 1, y = a^1 = a.
- Đồ thị của hàm số mũ luôn nằm phía trên trục hoành (y = a^x > 0 với mọi x thuộc R).

Những tính chất này giúp bạn hình dung và phân tích đồ thị của hàm số mũ một cách dễ dàng hơn.

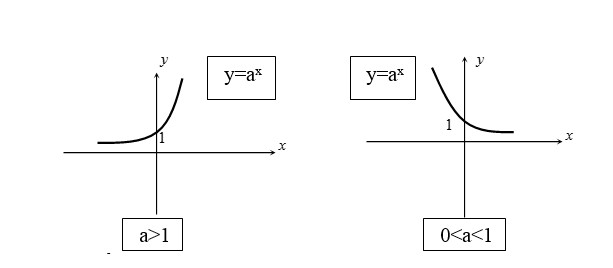
1.4. Đồ Thị Hàm Số Mũ

Đồ thị hàm số mũ là một đường cong đặc biệt, phản ánh rõ các tính chất của hàm số. Dưới đây là hình dạng tổng quát của đồ thị hàm số mũ:

Xét hàm số mũ y = a^x (a > 0; a ≠ 1)

Tập xác định: D = R.
Tập giá trị: T = (0; +∞).
Khi a > 1: Hàm số đồng biến.
Khi 0 < a < 1: Hàm số nghịch biến.

Đặc điểm đồ thị:

Đi qua điểm (0; 1).
Nằm phía trên trục hoành.
Nhận trục hoành làm tiệm cận ngang.

Hình ảnh minh họa đồ thị hàm số mũ với a > 1, thể hiện tính đồng biến và tiệm cận ngang.

Hình ảnh minh họa đồ thị hàm số mũ với 0 < a < 1, thể hiện tính nghịch biến và tiệm cận ngang.

Nhận xét:

Khi a > 1, đồ thị hàm số mũ có dạng một đường cong dốc lên từ trái sang phải. Đồ thị này tiến gần đến trục hoành khi x tiến tới âm vô cùng và tăng nhanh chóng khi x tiến tới dương vô cùng.
Khi 0 < a < 1, đồ thị hàm số mũ có dạng một đường cong dốc xuống từ trái sang phải. Đồ thị này tiến gần đến trục hoành khi x tiến tới dương vô cùng và tăng nhanh chóng khi x tiến tới âm vô cùng.

Việc nắm vững hình dạng và đặc điểm của đồ thị hàm số mũ giúp bạn giải quyết các bài toán liên quan đến hàm số này một cách trực quan và dễ dàng hơn.

2. Tìm Tập Xác Định Của Hàm Số Mũ

2.1. Định Nghĩa Tập Xác Định

Tập xác định (hay còn gọi là miền xác định) của một hàm số là tập hợp tất cả các giá trị mà biến số có thể nhận, sao cho hàm số đó có nghĩa (tức là cho ra một giá trị xác định). Nói cách khác, đó là tập hợp các giá trị đầu vào mà hàm số có thể xử lý.

Ví dụ:

Hàm số y = x^2 có tập xác định là R (tập hợp tất cả các số thực), vì bạn có thể thay bất kỳ số thực nào vào x và luôn nhận được một giá trị y tương ứng.
Hàm số y = 1/x có tập xác định là R {0} (tập hợp tất cả các số thực trừ số 0), vì bạn không thể chia cho 0.

Tầm quan trọng của việc tìm tập xác định:

Đảm bảo tính hợp lệ của hàm số: Việc tìm tập xác định giúp xác định những giá trị mà hàm số có nghĩa, tránh các trường hợp như chia cho 0, lấy căn bậc hai của số âm, hoặc logarit của số âm.
Khảo sát và vẽ đồ thị hàm số: Tập xác định là một yếu tố quan trọng để khảo sát sự biến thiên và vẽ đồ thị hàm số.
Giải quyết các bài toán ứng dụng: Trong các bài toán thực tế, tập xác định giúp xác định phạm vi giá trị có ý nghĩa của các biến số.

2.2. Điều Kiện Xác Định Của Hàm Số Mũ

Đối với hàm số mũ y = a^x, với a > 0 và a ≠ 1, điều kiện xác định như sau:

Nếu x là số thực bất kỳ: Hàm số mũ luôn xác định với mọi giá trị của x thuộc tập số thực R.
Nếu x là một biểu thức chứa biến: Ta cần xét điều kiện để biểu thức đó có nghĩa.

Ví dụ:

Hàm số y = 2^x có tập xác định là R, vì x có thể là bất kỳ số thực nào.
Hàm số y = 2^(1/x) có tập xác định là R {0}, vì x không thể bằng 0 (mẫu số phải khác 0).
Hàm số y = 2^(√x) có tập xác định là [0; +∞), vì x phải lớn hơn hoặc bằng 0 (biểu thức dưới căn phải không âm).

2.3. Các Bước Tìm Tập Xác Định Hàm Số Mũ

Để tìm tập xác định của hàm số mũ một cách hiệu quả, bạn có thể áp dụng các bước sau:

Bước 1: Xác định dạng của hàm số mũ.

Hàm số có dạng y = a^x hay y = a^(u(x)), trong đó u(x) là một biểu thức chứa biến x?

Bước 2: Xác định điều kiện để hàm số có nghĩa.

Nếu hàm số có dạng y = a^x, thì không có điều kiện gì cả. Tập xác định là R.
Nếu hàm số có dạng y = a^(u(x)), thì ta cần tìm điều kiện để biểu thức u(x) có nghĩa. Điều này có thể bao gồm:
- Mẫu số khác 0 (nếu u(x) là một phân thức).
- Biểu thức dưới căn bậc hai không âm (nếu u(x) chứa căn bậc hai).
- Biểu thức trong logarit dương (nếu u(x) chứa logarit).
- Các điều kiện khác tùy thuộc vào dạng của u(x).

Bước 3: Giải các phương trình và bất phương trình để tìm ra tập hợp các giá trị của x thỏa mãn điều kiện xác định.

Bước 4: Kết luận về tập xác định của hàm số.

2.4. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách tìm tập xác định của hàm số mũ, chúng ta sẽ cùng xét một số ví dụ sau:

Ví dụ 1: Tìm tập xác định của hàm số y = 5^(x^2 + 1).

Bước 1: Hàm số có dạng y = a^(u(x)), với a = 5 và u(x) = x^2 + 1.
Bước 2: Vì x^2 + 1 luôn dương với mọi giá trị của x, nên không có điều kiện gì cả.
Bước 3: Không cần giải phương trình hay bất phương trình.
Bước 4: Tập xác định của hàm số là R.

Ví dụ 2: Tìm tập xác định của hàm số y = 3^(1/(x - 2)).

Bước 1: Hàm số có dạng y = a^(u(x)), với a = 3 và u(x) = 1/(x - 2).
Bước 2: Điều kiện để hàm số có nghĩa là x - 2 ≠ 0.
Bước 3: Giải phương trình x - 2 ≠ 0, ta được x ≠ 2.
Bước 4: Tập xác định của hàm số là R {2}.

Ví dụ 3: Tìm tập xác định của hàm số y = 2^(√(4 - x)).

Bước 1: Hàm số có dạng y = a^(u(x)), với a = 2 và u(x) = √(4 - x).
Bước 2: Điều kiện để hàm số có nghĩa là 4 - x ≥ 0.
Bước 3: Giải bất phương trình 4 - x ≥ 0, ta được x ≤ 4.
Bước 4: Tập xác định của hàm số là (-∞; 4].

Ví dụ 4: Tìm tập xác định của hàm số y = ( (x + 2) / (x - 2) )^(-2018) - 3(16 - x^2)^(1 - √8) + 3.

Bước 1: Xác định dạng hàm số. Đây là một hàm số phức tạp, kết hợp nhiều yếu tố.
Bước 2: Xác định điều kiện để hàm số có nghĩa:
- (x + 2) / (x - 2) phải khác 0 và x - 2 phải khác 0 (do có mẫu số và số mũ âm). Điều này dẫn đến x ≠ -2 và x ≠ 2.
- 16 - x^2 > 0 (do có số mũ không nguyên). Điều này dẫn đến -4 < x < 4.
Bước 3: Giải các điều kiện trên, ta có:
- x ≠ -2
- x ≠ 2
- -4 < x < 4
Bước 4: Kết hợp các điều kiện, tập xác định của hàm số là (-4; 4) {-2; 2}.

3. Bài Tập Vận Dụng

Để củng cố kiến thức và rèn luyện kỹ năng tìm tập xác định của hàm số mũ, bạn hãy thử sức với các bài tập sau:

Tìm tập xác định của hàm số y = 7^(x/(x + 3)).
Tìm tập xác định của hàm số y = 4^(√(x - 1)).
Tìm tập xác định của hàm số y = 9^(1/(x^2 - 4)).
Tìm tập xác định của hàm số y = (x^2 - 1)^(x + 2).
Tìm tập xác định của hàm số y = e^(sin(x)).

Gợi ý:

Hãy áp dụng các bước đã hướng dẫn ở trên.
Chú ý đến các điều kiện xác định của phân thức, căn bậc hai, logarit (nếu có).
Sử dụng trục số hoặc biểu đồ để biểu diễn và kết hợp các điều kiện.

Bạn có thể tìm thêm các bài tập tương tự và lời giải chi tiết trên tic.edu.vn.

4. Hàm Số Logarit

4.1. Định Nghĩa Hàm Số Logarit

Hàm số logarit là hàm ngược của hàm số mũ. Hiểu một cách đơn giản, nếu hàm số mũ “hỏi” a mũ bao nhiêu để được x, thì hàm số logarit “hỏi” x là lũy thừa bậc mấy của a.

Theo định nghĩa, hàm số logarit cơ số a (với a > 0 và a ≠ 1) của x là hàm số được ký hiệu là:

y = logₐ(x)

Trong đó:

a là cơ số của logarit (phải dương và khác 1).
x là biểu thức lấy logarit (phải dương).
y là giá trị của logarit, tức là số mũ mà a phải được nâng lên để được x.

Ví dụ:

log₂(8) = 3 vì 2³ = 8.
log₁₀(100) = 2 vì 10² = 100.
logₑ(e) = 1 vì e¹ = e (với e là số Euler, khoảng 2.71828).

Mối quan hệ giữa hàm số mũ và hàm số logarit:

Hàm số mũ y = a^x và hàm số logarit y = logₐ(x) là hai hàm số ngược của nhau. Điều này có nghĩa là:

Nếu y = a^x thì x = logₐ(y).
Nếu y = logₐ(x) thì x = a^y.

Mối quan hệ này rất quan trọng để chuyển đổi giữa hai dạng hàm số và giải các bài toán liên quan.

4.2. Điều Kiện Xác Định Của Hàm Số Logarit

Để hàm số logarit có nghĩa, cần phải thỏa mãn các điều kiện sau:

Cơ số a phải dương và khác 1: a > 0 và a ≠ 1.
Biểu thức lấy logarit x phải dương: x > 0.

Giải thích:

Điều kiện a > 0 và a ≠ 1: Điều này xuất phát từ định nghĩa của hàm số logarit là hàm ngược của hàm số mũ. Hàm số mũ chỉ được định nghĩa khi cơ số dương và khác 1.
Điều kiện x > 0: Logarit của một số âm hoặc 0 không xác định trong tập số thực.

Ví dụ:

Hàm số y = log₂(x) có điều kiện xác định là x > 0.
Hàm số y = log₀.₅(x) có điều kiện xác định là x > 0.
Hàm số y = logₓ(5) có điều kiện xác định là x > 0 và x ≠ 1.
Hàm số y = log₂(x - 3) có điều kiện xác định là x - 3 > 0, tức là x > 3.

4.3. Các Bước Tìm Tập Xác Định Của Hàm Số Logarit

Để tìm tập xác định của hàm số logarit, bạn có thể thực hiện theo các bước sau:

Bước 1: Xác định dạng của hàm số logarit.

Hàm số có dạng y = logₐ(x) hay y = logᵤ(x)(v(x)), trong đó u(x) và v(x) là các biểu thức chứa biến x?

Bước 2: Xác định điều kiện để hàm số có nghĩa.

Nếu hàm số có dạng y = logₐ(x), thì điều kiện là x > 0 và a > 0, a ≠ 1.
Nếu hàm số có dạng y = logᵤ(x)(v(x)), thì ta cần tìm điều kiện để cả cơ số u(x) và biểu thức lấy logarit v(x) có nghĩa:
- u(x) > 0
- u(x) ≠ 1
- v(x) > 0

Bước 3: Giải các phương trình và bất phương trình để tìm ra tập hợp các giá trị của x thỏa mãn điều kiện xác định.

Bước 4: Kết luận về tập xác định của hàm số.

4.4. Ví Dụ Minh Họa

Để hiểu rõ hơn về cách tìm tập xác định của hàm số logarit, chúng ta sẽ cùng xét một số ví dụ sau:

Ví dụ 1: Tìm tập xác định của hàm số y = log₂(x + 1).

Bước 1: Hàm số có dạng y = logₐ(x), với a = 2 và biểu thức lấy logarit là x + 1.
Bước 2: Điều kiện để hàm số có nghĩa là x + 1 > 0.
Bước 3: Giải bất phương trình x + 1 > 0, ta được x > -1.
Bước 4: Tập xác định của hàm số là (-1; +∞).

Ví dụ 2: Tìm tập xác định của hàm số y = logₓ(x + 2).

Bước 1: Hàm số có dạng y = logᵤ(x)(v(x)), với cơ số u(x) = x và biểu thức lấy logarit v(x) = x + 2.
Bước 2: Điều kiện để hàm số có nghĩa là:
- x > 0
- x ≠ 1
- x + 2 > 0
Bước 3: Giải các điều kiện trên, ta có:
- x > 0
- x ≠ 1
- x > -2
Bước 4: Kết hợp các điều kiện, tập xác định của hàm số là (0; 1) ∪ (1; +∞).

Ví dụ 3: Tìm tập xác định của hàm số y = log₂(x² - 4x + 3).

Bước 1: Hàm số có dạng y = logₐ(x), với a = 2 và biểu thức lấy logarit là x² - 4x + 3.
Bước 2: Điều kiện để hàm số có nghĩa là x² - 4x + 3 > 0.
Bước 3: Giải bất phương trình x² - 4x + 3 > 0, ta được x < 1 hoặc x > 3.
Bước 4: Tập xác định của hàm số là (-∞; 1) ∪ (3; +∞).

5. Ứng Dụng Thực Tế

Việc nắm vững tập xác định của hàm số mũ và logarit không chỉ giúp bạn giải quyết các bài toán trong sách giáo khoa, mà còn có ứng dụng trong nhiều lĩnh vực thực tế:

Tính lãi kép trong tài chính: Hàm số mũ được sử dụng để tính lãi kép, giúp bạn dự đoán số tiền lãi thu được sau một khoảng thời gian nhất định. Việc xác định tập xác định của các biến số (ví dụ: lãi suất, thời gian gửi tiền) giúp bạn đưa ra các quyết định đầu tư hợp lý.
Mô hình hóa sự tăng trưởng dân số: Hàm số mũ được sử dụng để mô hình hóa sự tăng trưởng dân số theo thời gian. Tập xác định của các biến số (ví dụ: thời gian) giúp bạn giới hạn phạm vi dự đoán, tránh các kết quả phi thực tế.
Tính độ pH trong hóa học: Hàm số logarit được sử dụng để tính độ pH của một dung dịch. Độ pH chỉ có ý nghĩa trong một khoảng giá trị nhất định (thường từ 0 đến 14), do đó việc xác định tập xác định giúp bạn hiểu rõ hơn về tính chất của dung dịch.
Đo độ lớn của động đất: Thang Richter, một thang đo logarit, được sử dụng để đo độ lớn của động đất.

6. Lời Khuyên Khi Học Về Tập Xác Định Hàm Số Mũ

Nắm vững định nghĩa và tính chất: Hãy chắc chắn rằng bạn hiểu rõ định nghĩa và các tính chất cơ bản của hàm số mũ và logarit.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng.
Sử dụng công cụ hỗ trợ: Sử dụng máy tính cầm tay, phần mềm vẽ đồ thị, hoặc các công cụ trực tuyến để kiểm tra kết quả và trực quan hóa bài toán.
Tham khảo tài liệu: Đọc thêm sách tham khảo, tài liệu trên mạng, hoặc hỏi ý kiến thầy cô, bạn bè để hiểu sâu hơn về kiến thức.
Tìm kiếm sự giúp đỡ: Nếu bạn gặp khó khăn, đừng ngần ngại tìm kiếm sự giúp đỡ từ thầy cô, gia sư, hoặc các bạn học giỏi.
Liên hệ tic.edu.vn: Nếu bạn có bất kỳ thắc mắc nào, hãy liên hệ với tic.edu.vn qua email tic.edu@gmail.com hoặc truy cập website tic.edu.vn để được hỗ trợ.

7. Ưu Điểm Của Tic.edu.vn

So với các nguồn tài liệu và thông tin giáo dục khác, tic.edu.vn có những ưu điểm vượt trội sau:

Đa dạng: tic.edu.vn cung cấp nguồn tài liệu học tập phong phú, bao gồm lý thuyết, bài tập, đề thi, v.v. cho tất cả các môn học từ lớp 1 đến lớp 12.
Cập nhật: tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất, các xu hướng học tập tiên tiến, và các nguồn tài liệu mới.
Hữu ích: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất và đạt kết quả tốt hơn.
Cộng đồng hỗ trợ: tic.edu.vn xây dựng cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm, và nhận được sự giúp đỡ từ những người khác.
Miễn phí: Phần lớn tài liệu và công cụ trên tic.edu.vn đều được cung cấp miễn phí, giúp bạn tiết kiệm chi phí học tập.

8. Câu Hỏi Thường Gặp (FAQ)

Tập xác định của hàm số là gì?
Tập xác định của hàm số là tập hợp tất cả các giá trị mà biến số có thể nhận để hàm số có nghĩa.
Tại sao cần tìm tập xác định của hàm số?
Việc tìm tập xác định giúp đảm bảo tính hợp lệ của hàm số, khảo sát và vẽ đồ thị hàm số, và giải quyết các bài toán ứng dụng.
Điều kiện xác định của hàm số mũ là gì?
Đối với hàm số mũ y = a^x, điều kiện là a > 0 và a ≠ 1. Nếu x là một biểu thức chứa biến, ta cần xét thêm điều kiện để biểu thức đó có nghĩa.
Điều kiện xác định của hàm số logarit là gì?
Đối với hàm số logarit y = logₐ(x), điều kiện là a > 0, a ≠ 1, và x > 0.
Làm thế nào để tìm tập xác định của hàm số mũ?
Xác định dạng của hàm số, xác định điều kiện để hàm số có nghĩa, giải các phương trình và bất phương trình, và kết luận về tập xác định.
Làm thế nào để tìm tập xác định của hàm số logarit?
Xác định dạng của hàm số, xác định điều kiện để hàm số có nghĩa (cơ số dương và khác 1, biểu thức lấy logarit dương), giải các phương trình và bất phương trình, và kết luận về tập xác định.
Tôi có thể tìm thêm tài liệu học tập về hàm số mũ ở đâu?
Bạn có thể tìm thêm tài liệu trên tic.edu.vn, sách tham khảo, hoặc các trang web giáo dục uy tín.
Tôi có thể hỏi ai nếu tôi gặp khó khăn trong việc học về hàm số mũ?
Bạn có thể hỏi thầy cô, gia sư, bạn bè, hoặc tham gia các diễn đàn trực tuyến để được giải đáp thắc mắc.
tic.edu.vn có thể giúp tôi học về hàm số mũ như thế nào?
tic.edu.vn cung cấp nguồn tài liệu học tập phong phú, các công cụ hỗ trợ học tập trực tuyến, và một cộng đồng học tập sôi nổi để bạn trao đổi kiến thức và kinh nghiệm.
Làm sao để liên hệ với tic.edu.vn nếu tôi có thắc mắc?
Bạn có thể liên hệ với tic.edu.vn qua email tic.edu@gmail.com hoặc truy cập website tic.edu.vn.

9. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về hàm số mũ? Bạn mất thời gian để tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

tic.edu.vn cung cấp:

Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt.
Thông tin giáo dục mới nhất và chính xác.
Các công cụ hỗ trợ học tập trực tuyến hiệu quả.
Cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau.

Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn!

Truy cập tic.edu.vn ngay!