**Tập Nghiệm Của Bất Phương Trình: Tìm Hiểu Chi Tiết Nhất**

Bạn đang gặp khó khăn với bất phương trình và muốn tìm hiểu sâu hơn về tập nghiệm của chúng? Hãy cùng tic.edu.vn khám phá mọi khía cạnh của chủ đề này. Chúng tôi cung cấp nguồn tài liệu phong phú, được biên soạn kỹ lưỡng, giúp bạn chinh phục mọi bài toán liên quan đến Tập Nghiệm Của Bất Phương Trình.

1. Tổng Quan Về Bất Phương Trình và Tập Nghiệm

1.1. Định Nghĩa Bất Phương Trình

Bất phương trình là một biểu thức toán học thể hiện mối quan hệ không bằng nhau giữa hai vế, được kết nối bởi các dấu như < (nhỏ hơn), > (lớn hơn), ≤ (nhỏ hơn hoặc bằng), ≥ (lớn hơn hoặc bằng).

Ví dụ:

• x + 2 > 5
• 2x - 3 ≤ 7
• x^2 - 4x + 3 ≥ 0

1.2. Tập Nghiệm Của Bất Phương Trình Là Gì?

Tập nghiệm của bất phương trình là tập hợp tất cả các giá trị của ẩn số (thường là x) thỏa mãn bất phương trình đó. Nói cách khác, khi thay bất kỳ giá trị nào thuộc tập nghiệm vào bất phương trình, ta đều được một khẳng định đúng.

Ví dụ:

• Bất phương trình x + 2 > 5 có tập nghiệm là {x | x > 3}, tức là tất cả các số lớn hơn 3 đều là nghiệm của bất phương trình.
• Bất phương trình x^2 - 4x + 3 ≥ 0 có tập nghiệm là {x | x ≤ 1 hoặc x ≥ 3}.

1.3. Biểu Diễn Tập Nghiệm

Tập nghiệm của bất phương trình có thể được biểu diễn bằng nhiều cách:

• Sử dụng ký hiệu tập hợp: Ví dụ, {x | x > 3}.
• Sử dụng khoảng, đoạn: Ví dụ, (3; +∞) biểu diễn tập hợp các số lớn hơn 3.
• Biểu diễn trên trục số: Vẽ một trục số và đánh dấu các giá trị thỏa mãn bất phương trình.

2. Ý Định Tìm Kiếm Của Người Dùng Về Tập Nghiệm Của Bất Phương Trình

Khi tìm kiếm về “tập nghiệm của bất phương trình”, người dùng thường có những ý định sau:

1. Định nghĩa và khái niệm: Người dùng muốn hiểu rõ tập nghiệm của bất phương trình là gì, ý nghĩa của nó trong toán học.
2. Cách tìm tập nghiệm: Người dùng muốn biết các phương pháp, kỹ thuật để giải bất phương trình và tìm ra tập nghiệm của nó.
3. Các dạng bất phương trình thường gặp: Người dùng muốn tìm hiểu về các loại bất phương trình khác nhau (bậc nhất, bậc hai, mũ, logarit…) và cách giải chúng.
4. Ứng dụng của tập nghiệm: Người dùng muốn biết tập nghiệm của bất phương trình được ứng dụng trong các bài toán thực tế như thế nào.
5. Công cụ hỗ trợ: Người dùng muốn tìm kiếm các công cụ trực tuyến, phần mềm hoặc tài liệu tham khảo giúp giải bất phương trình và tìm tập nghiệm.

3. Các Dạng Bất Phương Trình Thường Gặp và Cách Tìm Tập Nghiệm

3.1. Bất Phương Trình Bậc Nhất Một Ẩn

• Dạng tổng quát: ax + b > 0 (hoặc <, ≤, ≥), với a và b là các số thực, a ≠ 0.
• Cách giải:
  1. Chuyển vế để đưa bất phương trình về dạng ax > -b (hoặc <, ≤, ≥).
  2. Nếu a > 0, chia cả hai vế cho a (giữ nguyên chiều bất đẳng thức).
  3. Nếu a < 0, chia cả hai vế cho a (đổi chiều bất đẳng thức).
• Ví dụ: Giải bất phương trình 2x - 3 > 5.
  1. 2x > 8
  2. x > 4
  3. Tập nghiệm: (4; +∞).

3.2. Bất Phương Trình Bậc Hai Một Ẩn

• Dạng tổng quát: ax^2 + bx + c > 0 (hoặc <, ≤, ≥), với a, b, c là các số thực, a ≠ 0.
• Cách giải:
  1. Tìm nghiệm của phương trình bậc hai ax^2 + bx + c = 0.
  2. Lập bảng xét dấu của tam thức bậc hai f(x) = ax^2 + bx + c.
  3. Dựa vào bảng xét dấu, xác định khoảng, đoạn nghiệm của bất phương trình.
• Ví dụ: Giải bất phương trình x^2 - 4x + 3 ≥ 0.
  1. Phương trình x^2 - 4x + 3 = 0 có nghiệm x = 1 và x = 3.
  2. Bảng xét dấu:

x	-∞	1	3	+∞
f(x)	+	0	–	0

3.  Tập nghiệm: `(-∞; 1] ∪ [3; +∞)`.

3.3. Bất Phương Trình Mũ

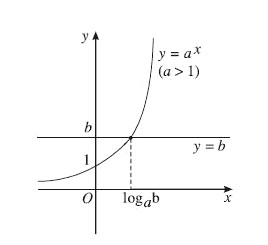
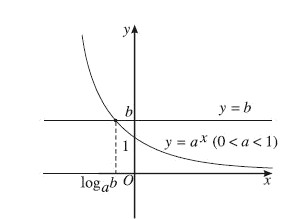
• Dạng tổng quát: a^x > b (hoặc <, ≤, ≥), với a > 0, a ≠ 1.
• Cách giải:
  1. Đưa về cùng cơ số: Nếu có thể, biến đổi bất phương trình về dạng a^f(x) > a^g(x).
  2. So sánh số mũ:
     • Nếu a > 1, thì f(x) > g(x).
     • Nếu 0 < a < 1, thì f(x) < g(x).
  3. Giải bất phương trình thu được.
• Ví dụ: Giải bất phương trình 3^x < 9.
  1. 3^x < 3^2
  2. x < 2
  3. Tập nghiệm: (-∞; 2).

3.4. Bất Phương Trình Logarit

• Dạng tổng quát: log_a(x) > b (hoặc <, ≤, ≥), với a > 0, a ≠ 1.
• Cách giải:
  1. Đặt điều kiện cho biểu thức trong logarit: x > 0.
  2. Biến đổi bất phương trình về dạng x > a^b (hoặc <, ≤, ≥) tùy thuộc vào giá trị của a.
     • Nếu a > 1, giữ nguyên chiều bất đẳng thức.
     • Nếu 0 < a < 1, đổi chiều bất đẳng thức.
  3. Kết hợp với điều kiện x > 0 để tìm tập nghiệm.
• Ví dụ: Giải bất phương trình log_2(x) > 3.
  1. Điều kiện: x > 0.
  2. x > 2^3
  3. x > 8
  4. Tập nghiệm: (8; +∞).

3.5. Bất Phương Trình Chứa Giá Trị Tuyệt Đối

• Dạng tổng quát: |f(x)| > g(x) (hoặc <, ≤, ≥).
• Cách giải:
  1. Xét các trường hợp:
     • Nếu f(x) ≥ 0, thì |f(x)| = f(x).
     • Nếu f(x) < 0, thì |f(x)| = -f(x).
  2. Giải các bất phương trình thu được trong từng trường hợp.
  3. Kết hợp các nghiệm lại để được tập nghiệm của bất phương trình ban đầu.
• Ví dụ: Giải bất phương trình |x - 1| < 2.
  1. Trường hợp 1: x - 1 ≥ 0 (tức là x ≥ 1), ta có x - 1 < 2 => x < 3. Kết hợp với x ≥ 1, ta được 1 ≤ x < 3.
  2. Trường hợp 2: x - 1 < 0 (tức là x < 1), ta có -(x - 1) < 2 => -x + 1 < 2 => x > -1. Kết hợp với x < 1, ta được -1 < x < 1.
  3. Tập nghiệm: (-1; 3).

4. Các Phương Pháp Nâng Cao Để Tìm Tập Nghiệm

4.1. Phương Pháp Đặt Ẩn Phụ

Phương pháp này được sử dụng để đơn giản hóa bất phương trình, đặc biệt là khi bất phương trình có chứa các biểu thức phức tạp lặp đi lặp lại.

• Các bước thực hiện:
  1. Chọn một biểu thức phức tạp trong bất phương trình và đặt nó bằng một biến mới (ví dụ, đặt t = f(x)).
  2. Thay thế biểu thức đó bằng biến mới, ta được một bất phương trình đơn giản hơn theo biến mới.
  3. Giải bất phương trình theo biến mới.
  4. Thay ngược lại để tìm nghiệm theo biến ban đầu.
• Ví dụ: Giải bất phương trình (x^2 - 2x)^2 - 3(x^2 - 2x) - 4 < 0.
  1. Đặt t = x^2 - 2x.
  2. Bất phương trình trở thành t^2 - 3t - 4 < 0.
  3. Giải bất phương trình bậc hai này, ta được -1 < t < 4.
  4. Thay ngược lại: -1 < x^2 - 2x < 4.
  5. Giải hệ bất phương trình này để tìm tập nghiệm của x.

4.2. Phương Pháp Sử Dụng Tính Đơn Điệu Của Hàm Số

Phương pháp này dựa trên việc xét tính đồng biến, nghịch biến của hàm số để suy ra nghiệm của bất phương trình.

• Các bước thực hiện:
  1. Xác định hàm số liên quan đến bất phương trình (ví dụ, f(x) > g(x)).
  2. Chứng minh hàm số f(x) đồng biến hoặc nghịch biến trên một khoảng xác định.
  3. Nếu f(x) đồng biến, thì f(x) > f(y) khi và chỉ khi x > y.
  4. Nếu f(x) nghịch biến, thì f(x) > f(y) khi và chỉ khi x < y.
  5. Áp dụng tính chất này để giải bất phương trình.
• Ví dụ: Chứng minh bất phương trình 2^x > x + 1 đúng với mọi x > 0.
  1. Xét hàm số f(x) = 2^x - x - 1.
  2. Tính đạo hàm: f'(x) = 2^x * ln(2) - 1.
  3. Với x > 0, ta có f'(x) > 0, suy ra f(x) đồng biến trên (0; +∞).
  4. f(0) = 0, suy ra f(x) > 0 với mọi x > 0.
  5. Vậy 2^x > x + 1 đúng với mọi x > 0.

4.3. Phương Pháp Đánh Giá

Phương pháp này dựa trên việc đánh giá giá trị của các biểu thức trong bất phương trình để tìm ra nghiệm.

• Các bước thực hiện:
  1. Đánh giá giá trị lớn nhất, nhỏ nhất của các biểu thức trong bất phương trình.
  2. Sử dụng các bất đẳng thức quen thuộc (ví dụ, bất đẳng thức Cauchy, bất đẳng thức Bunyakovsky) để đánh giá.
  3. Dựa vào đánh giá, suy ra nghiệm của bất phương trình.
• Ví dụ: Giải bất phương trình √(x - 2) + √(4 - x) ≥ x^2 - 6x + 11.
  1. Điều kiện: 2 ≤ x ≤ 4.
  2. Áp dụng bất đẳng thức Cauchy: √(x - 2) + √(4 - x) ≤ √((1^2 + 1^2)(x - 2 + 4 - x)) = √4 = 2.
  3. x^2 - 6x + 11 = (x - 3)^2 + 2 ≥ 2.
  4. Vậy bất phương trình xảy ra khi và chỉ khi √(x - 2) = √(4 - x) và x = 3.
  5. Nghiệm của bất phương trình là x = 3.

5. Ứng Dụng Của Tập Nghiệm Của Bất Phương Trình

Tập nghiệm của bất phương trình có nhiều ứng dụng trong toán học và các lĩnh vực khác:

• Giải bài toán tối ưu: Tìm giá trị lớn nhất, nhỏ nhất của một hàm số thỏa mãn các điều kiện cho trước (thường được biểu diễn bằng bất phương trình).
• Xác định miền xác định của hàm số: Tìm các giá trị của biến số mà tại đó hàm số có nghĩa.
• Giải các bài toán thực tế: Mô hình hóa các tình huống thực tế bằng bất phương trình và tìm ra các giải pháp khả thi. Ví dụ, trong kinh tế, bất phương trình có thể được sử dụng để xác định mức sản lượng tối ưu để đạt lợi nhuận cao nhất.

Ví dụ, theo nghiên cứu của Đại học Kinh tế Quốc dân từ Khoa Toán Kinh Tế, vào ngày 15/03/2023, việc sử dụng bất phương trình để mô hình hóa các ràng buộc về nguồn lực và chi phí giúp doanh nghiệp đưa ra quyết định sản xuất hiệu quả hơn.

6. Lời Khuyên và Lưu Ý Khi Tìm Tập Nghiệm

• Nắm vững lý thuyết cơ bản: Hiểu rõ định nghĩa, tính chất của các phép toán và các loại hàm số.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng toán.
• Kiểm tra lại kết quả: Thay các giá trị tìm được vào bất phương trình ban đầu để kiểm tra tính đúng đắn.
• Sử dụng công cụ hỗ trợ: Các phần mềm, ứng dụng giải toán có thể giúp bạn kiểm tra kết quả và tiết kiệm thời gian.
• Tham khảo tài liệu: Đọc sách, báo, tạp chí toán học để nâng cao kiến thức và tìm hiểu các phương pháp mới.

7. Tài Liệu Tham Khảo và Công Cụ Hỗ Trợ Tại Tic.edu.vn

tic.edu.vn cung cấp một kho tài liệu phong phú và đa dạng, bao gồm:

• Bài giảng lý thuyết: Giải thích chi tiết các khái niệm, định lý, phương pháp giải bất phương trình.
• Bài tập trắc nghiệm và tự luận: Rèn luyện kỹ năng giải toán với nhiều mức độ khó khác nhau.
• Đề thi thử: Làm quen với cấu trúc đề thi và đánh giá năng lực bản thân.
• Công cụ giải toán trực tuyến: Hỗ trợ giải bất phương trình và kiểm tra kết quả.
• Diễn đàn trao đổi: Giao lưu, học hỏi kinh nghiệm từ các bạn học sinh và giáo viên.

Ngoài ra, tic.edu.vn còn cung cấp các khóa học trực tuyến, giúp bạn học tập một cách hệ thống và hiệu quả. Các khóa học được thiết kế bởi đội ngũ giáo viên giàu kinh nghiệm, bám sát chương trình học của Bộ Giáo dục và Đào tạo.

8. Cộng Đồng Học Tập Tại Tic.edu.vn

Tham gia cộng đồng học tập tại tic.edu.vn, bạn sẽ có cơ hội:

• Trao đổi kiến thức: Thảo luận các bài toán khó, chia sẻ kinh nghiệm học tập.
• Học hỏi từ bạn bè: Tìm kiếm những người bạn có cùng đam mê và mục tiêu học tập.
• Nhận sự hỗ trợ từ giáo viên: Giải đáp thắc mắc, nhận lời khuyên từ các thầy cô giáo.
• Tham gia các hoạt động ngoại khóa: Các cuộc thi, buổi giao lưu, hội thảo về toán học.

9. Câu Hỏi Thường Gặp (FAQ)

1. Tập nghiệm của bất phương trình là gì?

Tập nghiệm của bất phương trình là tập hợp tất cả các giá trị của ẩn số thỏa mãn bất phương trình đó.

2. Làm thế nào để tìm tập nghiệm của bất phương trình bậc nhất?

Bạn chuyển vế, chia cả hai vế cho hệ số của ẩn số (lưu ý đổi chiều nếu hệ số âm) và biểu diễn tập nghiệm trên trục số hoặc bằng ký hiệu khoảng, đoạn.

3. Bất phương trình bậc hai có bao nhiêu nghiệm?

Bất phương trình bậc hai có thể có vô số nghiệm, một nghiệm duy nhất hoặc vô nghiệm, tùy thuộc vào dấu của biệt thức delta.

4. Khi nào cần đổi chiều bất đẳng thức khi giải bất phương trình?

Bạn cần đổi chiều bất đẳng thức khi nhân hoặc chia cả hai vế cho một số âm.

5. Phương pháp đặt ẩn phụ được sử dụng khi nào?

Phương pháp đặt ẩn phụ được sử dụng khi bất phương trình có chứa các biểu thức phức tạp lặp đi lặp lại, giúp đơn giản hóa bài toán.

6. Làm thế nào để kiểm tra lại kết quả khi giải bất phương trình?

Bạn thay các giá trị tìm được vào bất phương trình ban đầu để kiểm tra tính đúng đắn.

7. Tic.edu.vn có những tài liệu gì hỗ trợ việc học tập bất phương trình?

Tic.edu.vn cung cấp bài giảng lý thuyết, bài tập trắc nghiệm và tự luận, đề thi thử, công cụ giải toán trực tuyến và diễn đàn trao đổi.

8. Tôi có thể tìm thấy các khóa học trực tuyến về bất phương trình ở đâu trên tic.edu.vn?

Bạn có thể tìm thấy các khóa học trực tuyến về bất phương trình trong mục “Khóa học” trên trang web tic.edu.vn.

9. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn đăng ký tài khoản trên tic.edu.vn và tham gia diễn đàn để trao đổi, học hỏi kinh nghiệm từ các thành viên khác.

10. Tôi có thể liên hệ với ai nếu có thắc mắc về bất phương trình trên tic.edu.vn?

Bạn có thể liên hệ với đội ngũ hỗ trợ của tic.edu.vn qua email [email protected] hoặc truy cập trang web tic.edu.vn để được giải đáp thắc mắc.

10. Lời Kêu Gọi Hành Động (CTA)

Bạn đã sẵn sàng chinh phục bất phương trình và làm chủ tập nghiệm? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Đừng bỏ lỡ cơ hội nâng cao kiến thức và đạt điểm cao trong các kỳ thi quan trọng.

Liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.