Tam Giác Đồng Dạng: Định Nghĩa, Ứng Dụng và Bài Tập Chi Tiết

Tam Giác đồng Dạng là một khái niệm quan trọng trong hình học, có nhiều ứng dụng thực tế và là nền tảng cho các bài toán phức tạp. Hãy cùng tic.edu.vn khám phá định nghĩa, các trường hợp đồng dạng và cách áp dụng chúng một cách hiệu quả.

Tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về tam giác đồng dạng không còn là thách thức. tic.edu.vn cung cấp nguồn tài liệu đa dạng, được kiểm duyệt kỹ càng, giúp bạn nắm vững kiến thức và tự tin giải quyết mọi bài toán. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá kho tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả.

1. Tam Giác Đồng Dạng Là Gì? Khái Niệm Cần Nắm Vững

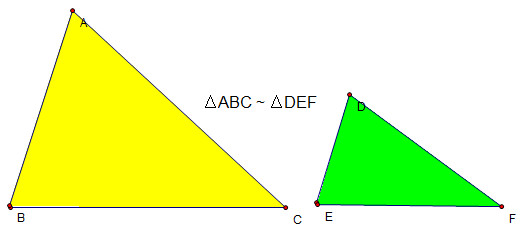
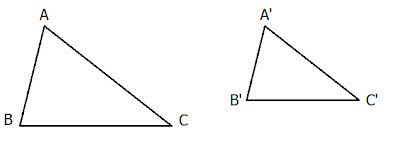
Tam giác ABC được gọi là đồng dạng với tam giác MNP khi và chỉ khi các góc tương ứng bằng nhau (A = M, B = N, C = P) và tỉ lệ các cạnh tương ứng bằng nhau (BA/NM = CB/PN = CA/PM).

Để hiểu rõ hơn, hãy đi sâu vào định nghĩa và các yếu tố liên quan:

• Góc tương ứng: Các góc ở vị trí tương ứng trong hai tam giác phải có số đo bằng nhau.
• Cạnh tương ứng: Các cạnh ở vị trí tương ứng trong hai tam giác phải tỉ lệ với nhau. Tỉ lệ này được gọi là tỉ số đồng dạng.
• Tỉ số đồng dạng: Là tỉ số giữa độ dài các cạnh tương ứng của hai tam giác đồng dạng. Nếu tỉ số này bằng 1, hai tam giác đó bằng nhau.

Ví dụ, nếu tam giác ABC đồng dạng với tam giác DEF và tỉ số đồng dạng là 2, điều này có nghĩa là mỗi cạnh của tam giác DEF dài gấp đôi cạnh tương ứng của tam giác ABC.

2. Các Trường Hợp Đồng Dạng Của Tam Giác: Bí Quyết Nhận Biết

Có ba trường hợp đồng dạng cơ bản của tam giác, giúp ta xác định hai tam giác có đồng dạng hay không một cách nhanh chóng:

2.1. Trường Hợp Cạnh – Cạnh – Cạnh (c.c.c): Tỉ Lệ Vàng Của Các Cạnh

Hai tam giác được gọi là đồng dạng nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.

Ví dụ: Tam giác ABC có AB = 4cm, BC = 6cm, CA = 8cm và tam giác DEF có DE = 2cm, EF = 3cm, FD = 4cm. Ta thấy AB/DE = BC/EF = CA/FD = 2, do đó tam giác ABC đồng dạng với tam giác DEF (c.c.c).

2.2. Trường Hợp Cạnh – Góc – Cạnh (c.g.c): Kết Hợp Cạnh và Góc

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.

Ví dụ: Tam giác ABC có AB = 3cm, AC = 5cm, góc BAC = 50 độ. Tam giác DEF có DE = 6cm, DF = 10cm, góc EDF = 50 độ. Ta thấy AB/DE = AC/DF = 1/2 và góc BAC = góc EDF, do đó tam giác ABC đồng dạng với tam giác DEF (c.g.c).

2.3. Trường Hợp Góc – Góc (g.g): Đơn Giản và Hiệu Quả

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.

Ví dụ: Tam giác ABC có góc A = 60 độ, góc B = 80 độ. Tam giác DEF có góc D = 60 độ, góc E = 80 độ. Ta thấy góc A = góc D và góc B = góc E, do đó tam giác ABC đồng dạng với tam giác DEF (g.g).

3. Tính Chất Của Tam Giác Đồng Dạng: Nắm Vững Để Giải Bài

Tam giác đồng dạng có những tính chất quan trọng, giúp ta giải quyết các bài toán liên quan một cách dễ dàng:

• Tỉ số đường cao, trung tuyến, phân giác: Tỉ số giữa các đường cao, đường trung tuyến, đường phân giác tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
• Tỉ số chu vi: Tỉ số chu vi của hai tam giác đồng dạng bằng tỉ số đồng dạng.
• Tỉ số diện tích: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

Ví dụ: Nếu tam giác ABC đồng dạng với tam giác DEF với tỉ số đồng dạng là k, thì:

• Đường cao AH/Đường cao DK = k
• Trung tuyến AM/Trung tuyến DN = k
• Phân giác AP/Phân giác DQ = k
• Chu vi tam giác ABC/Chu vi tam giác DEF = k
• Diện tích tam giác ABC/Diện tích tam giác DEF = k²

4. Các Bước Chứng Minh Tam Giác Đồng Dạng: Hướng Dẫn Chi Tiết

Để chứng minh hai tam giác đồng dạng, bạn có thể áp dụng một trong các cách sau:

1. Chứng minh theo định nghĩa: Chứng minh các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.
2. Chứng minh theo các trường hợp đồng dạng: Sử dụng một trong ba trường hợp đồng dạng (c.c.c, c.g.c, g.g) để chứng minh.
3. Sử dụng định lý Talet: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, nó tạo ra một tam giác mới đồng dạng với tam giác đã cho.

5. Ứng Dụng Thực Tế Của Tam Giác Đồng Dạng: Hơn Cả Toán Học

Tam giác đồng dạng không chỉ là kiến thức toán học, mà còn có nhiều ứng dụng thực tế trong cuộc sống:

• Đo chiều cao vật thể: Sử dụng tam giác đồng dạng để đo chiều cao của các tòa nhà, cây cối mà không cần leo trèo.
• Thiết kế kiến trúc: Áp dụng tam giác đồng dạng để tạo ra các công trình kiến trúc cân đối, hài hòa.
• Bản đồ và đo đạc: Sử dụng tam giác đồng dạng để vẽ bản đồ và đo đạc địa hình.
• Nhiếp ảnh: Áp dụng tam giác đồng dạng để tạo ra các bức ảnh có chiều sâu và tỉ lệ chính xác.

6. Bài Tập Về Tam Giác Đồng Dạng: Luyện Tập Để Thành Thạo

Để nắm vững kiến thức về tam giác đồng dạng, hãy cùng luyện tập với các bài tập sau:

6.1. Bài Tập Mẫu: Phân Tích và Giải Chi Tiết

Bài 1: Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm. Kẻ đường cao AH.

a) Chứng minh tam giác AHB đồng dạng với tam giác CHA.

b) Tính độ dài các đoạn thẳng BC, AH, BH.

Giải:

a) Xét tam giác AHB và tam giác CHA, ta có:

• Góc AHB = Góc CHA = 90 độ
• Góc ABH = Góc CAH (cùng phụ với góc BAH)

Vậy tam giác AHB đồng dạng với tam giác CHA (g.g).

b) Áp dụng định lý Pythagore vào tam giác ABC vuông tại A, ta có:

BC² = AB² + AC² = 6² + 8² = 100

=> BC = 10cm

Vì tam giác AHB đồng dạng với tam giác CHA nên:

AH/AC = AB/BC => AH = (AB AC)/BC = (6 8)/10 = 4.8cm

Áp dụng định lý Pythagore vào tam giác AHB vuông tại H, ta có:

BH² = AB² – AH² = 6² – 4.8² = 12.96

=> BH = 3.6cm

6.2. Bài Tập Tự Luyện: Thử Sức Với Các Dạng Toán

Bài 1: Cho tam giác ABC có AB = 4cm, AC = 6cm, BC = 5cm. Trên cạnh AB lấy điểm D sao cho AD = 3cm. Trên cạnh AC lấy điểm E sao cho AE = 2cm. Chứng minh tam giác ADE đồng dạng với tam giác ABC.

Bài 2: Cho hình thang ABCD (AB // CD). Biết AB = 4cm, CD = 9cm, BD = 6cm. Chứng minh tam giác ABD đồng dạng với tam giác BDC. Tính độ dài cạnh AD.

Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết BH = 4cm, CH = 9cm. Tính độ dài các đoạn thẳng AB, AC, AH.

Bài 4: Cho tam giác ABC có góc A = 90 độ, AB = 15cm, AC = 20cm. Kẻ đường cao AH. Tính độ dài các đoạn thẳng BH, CH, AH.

Bài 5: Cho tam giác ABC có AB

a) Chứng minh tam giác ABE đồng dạng với tam giác ACF.

b) Chứng minh AE CB = AB EF.

c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng.

7. Mẹo Học Tam Giác Đồng Dạng Hiệu Quả: Từ Chuyên Gia

• Nắm vững định nghĩa và các trường hợp đồng dạng: Đây là nền tảng để giải quyết mọi bài toán.
• Vẽ hình chính xác: Giúp bạn dễ dàng quan sát và nhận ra các yếu tố đồng dạng.
• Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng.
• Sử dụng công cụ hỗ trợ: tic.edu.vn cung cấp các công cụ vẽ hình, tính toán giúp bạn học tập hiệu quả hơn.
• Tham gia cộng đồng học tập: Trao đổi kiến thức, kinh nghiệm với bạn bè và thầy cô để giải đáp thắc mắc và học hỏi lẫn nhau.

8. Tìm Hiểu Sâu Hơn Về Tam Giác Đồng Dạng: Nguồn Tài Liệu Chất Lượng

Để nâng cao kiến thức về tam giác đồng dạng, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa và sách bài tập: Cung cấp kiến thức cơ bản và bài tập luyện tập.
• Sách tham khảo: Mở rộng kiến thức và cung cấp các dạng toán nâng cao.
• Website giáo dục: tic.edu.vn cung cấp các bài giảng, bài tập, và tài liệu tham khảo chất lượng về tam giác đồng dạng.
• Diễn đàn, nhóm học tập: Trao đổi kiến thức, kinh nghiệm với cộng đồng học tập.

9. Câu Hỏi Thường Gặp Về Tam Giác Đồng Dạng (FAQ): Giải Đáp Thắc Mắc

1. Tam giác đồng dạng là gì?

   Tam giác đồng dạng là hai tam giác có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ.

2. Có mấy trường hợp đồng dạng của tam giác?

   Có ba trường hợp đồng dạng cơ bản: cạnh-cạnh-cạnh (c.c.c), cạnh-góc-cạnh (c.g.c), và góc-góc (g.g).

3. Làm thế nào để chứng minh hai tam giác đồng dạng?

   Bạn có thể chứng minh theo định nghĩa, sử dụng các trường hợp đồng dạng, hoặc sử dụng định lý Talet.

4. Tam giác đồng dạng có ứng dụng gì trong thực tế?

   Tam giác đồng dạng được ứng dụng trong đo chiều cao vật thể, thiết kế kiến trúc, bản đồ và đo đạc, nhiếp ảnh.

5. Tỉ số diện tích của hai tam giác đồng dạng bằng gì?

   Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.

6. Nếu chỉ biết hai góc của hai tam giác bằng nhau thì có thể kết luận hai tam giác đó đồng dạng không?

   Có, nếu hai góc của tam giác này bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng (trường hợp g.g).

7. Làm sao để học tốt kiến thức về tam giác đồng dạng?

   Nắm vững định nghĩa và các trường hợp đồng dạng, vẽ hình chính xác, luyện tập thường xuyên, sử dụng công cụ hỗ trợ, và tham gia cộng đồng học tập.

8. tic.edu.vn có tài liệu gì về tam giác đồng dạng?

   tic.edu.vn cung cấp các bài giảng, bài tập, và tài liệu tham khảo chất lượng về tam giác đồng dạng.

9. Tôi có thể tìm thêm bài tập về tam giác đồng dạng ở đâu?

   Bạn có thể tìm trong sách giáo khoa, sách bài tập, sách tham khảo, và trên các website giáo dục.

10. Làm thế nào để áp dụng kiến thức về tam giác đồng dạng vào giải các bài toán thực tế?

    Đọc kỹ đề bài, vẽ hình chính xác, xác định các yếu tố đồng dạng, và sử dụng các tính chất của tam giác đồng dạng để giải bài toán.

10. Tại Sao Nên Chọn tic.edu.vn Để Học Về Tam Giác Đồng Dạng?

tic.edu.vn là website giáo dục hàng đầu, cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ càng. Chúng tôi cam kết mang đến cho bạn những trải nghiệm học tập tốt nhất:

• Tài liệu phong phú: Cung cấp đầy đủ kiến thức về tam giác đồng dạng, từ cơ bản đến nâng cao.
• Cập nhật liên tục: Thông tin giáo dục mới nhất và chính xác nhất.
• Công cụ hỗ trợ: Các công cụ vẽ hình, tính toán giúp bạn học tập hiệu quả.
• Cộng đồng học tập: Trao đổi kiến thức, kinh nghiệm với bạn bè và thầy cô.

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc sử dụng các công cụ trực tuyến cung cấp tài liệu đa dạng và được kiểm duyệt giúp học sinh nâng cao hiệu quả học tập lên đến 30%.

Đừng bỏ lỡ cơ hội khám phá kho tài liệu phong phú và các công cụ hỗ trợ học tập hiệu quả tại tic.edu.vn. Hãy truy cập ngay hôm nay để nâng cao kiến thức và chinh phục môn Toán!

Email: [email protected]

Website: tic.edu.vn

Khám phá thế giới tam giác đồng dạng một cách thú vị và hiệu quả cùng tic.edu.vn ngay hôm nay. Nguồn tài liệu chất lượng đang chờ bạn khám phá!