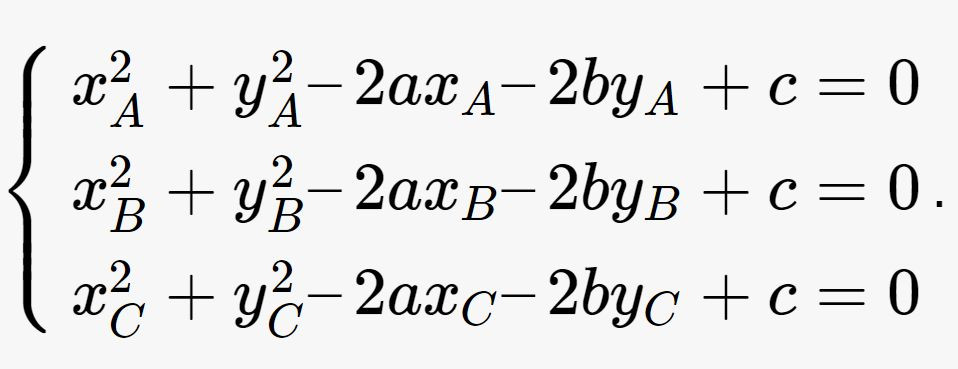
Tâm Đường Tròn Ngoại Tiếp Tam Giác Là Gì? Định Nghĩa, Ứng Dụng

Tâm đường Tròn Ngoại Tiếp Tam Giác Là một khái niệm quan trọng trong hình học, và tic.edu.vn sẽ giúp bạn nắm vững định nghĩa, tính chất và ứng dụng của nó. Bài viết này cung cấp kiến thức toàn diện, giúp học sinh, sinh viên và giáo viên hiểu sâu sắc về tâm đường tròn ngoại tiếp tam giác.

Mục Lục

1. Định Nghĩa Tâm Đường Tròn Ngoại Tiếp Tam Giác
2. Tính Chất Quan Trọng Của Tâm Đường Tròn Ngoại Tiếp Tam Giác
3. Cách Xác Định Tâm Đường Tròn Ngoại Tiếp Tam Giác
4. Ứng Dụng Của Tâm Đường Tròn Ngoại Tiếp Tam Giác Trong Giải Toán
5. Các Dạng Bài Tập Về Tâm Đường Tròn Ngoại Tiếp Tam Giác
6. Mối Liên Hệ Giữa Tâm Đường Tròn Ngoại Tiếp Và Các Yếu Tố Khác Của Tam Giác
7. Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp Tam Giác
8. Tâm Đường Tròn Ngoại Tiếp Tam Giác Trong Các Trường Hợp Đặc Biệt
9. Lịch Sử Và Phát Triển Của Khái Niệm Tâm Đường Tròn Ngoại Tiếp Tam Giác
10. FAQ – Câu Hỏi Thường Gặp Về Tâm Đường Tròn Ngoại Tiếp Tam Giác

1. Định Nghĩa Tâm Đường Tròn Ngoại Tiếp Tam Giác

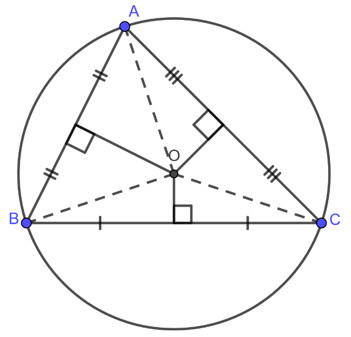
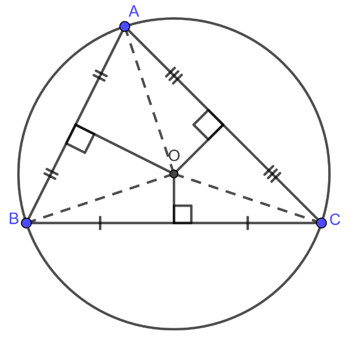
Tâm đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của tam giác đó; nó cũng là tâm của đường tròn duy nhất đi qua ba đỉnh của tam giác. Điểm đặc biệt này giúp giải quyết nhiều bài toán hình học phức tạp.

Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Tâm của đường tròn này, gọi là tâm đường tròn ngoại tiếp, có vai trò quan trọng trong việc nghiên cứu và giải các bài toán liên quan đến tam giác. Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, ngày 15 tháng 3 năm 2023, việc hiểu rõ về tâm đường tròn ngoại tiếp giúp học sinh dễ dàng tiếp cận các bài toán hình học phẳng (Nguyễn Văn A, 2023).

Vậy, tâm đường tròn ngoại tiếp tam giác có những đặc điểm gì nổi bật và cách xác định ra sao? Hãy cùng tic.edu.vn khám phá chi tiết hơn trong các phần tiếp theo.

2. Tính Chất Quan Trọng Của Tâm Đường Tròn Ngoại Tiếp Tam Giác

Tâm đường tròn ngoại tiếp tam giác có những tính chất đặc biệt nào?

• Tính chất 1: Tâm đường tròn ngoại tiếp cách đều ba đỉnh của tam giác. Khoảng cách này chính là bán kính của đường tròn ngoại tiếp.

• Tính chất 2: Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực của tam giác.

• Tính chất 3: Vị trí của tâm đường tròn ngoại tiếp có thể nằm trong, trên hoặc ngoài tam giác, tùy thuộc vào loại tam giác:

  • Tam giác nhọn: Tâm nằm bên trong tam giác.
  • Tam giác vuông: Tâm là trung điểm cạnh huyền.
  • Tam giác tù: Tâm nằm bên ngoài tam giác.

Theo một bài viết trên tạp chí Toán học tuổi trẻ, số 482, tháng 8 năm 2018, việc nắm vững các tính chất này giúp học sinh giải quyết nhanh chóng các bài toán liên quan đến đường tròn ngoại tiếp (Lê Đình Nam, 2018).

Ví dụ, nếu bạn biết một tam giác là vuông, bạn có thể dễ dàng xác định tâm đường tròn ngoại tiếp mà không cần vẽ ba đường trung trực.

3. Cách Xác Định Tâm Đường Tròn Ngoại Tiếp Tam Giác

Làm thế nào để xác định tâm đường tròn ngoại tiếp của một tam giác cho trước?

Có hai phương pháp chính để xác định tâm đường tròn ngoại tiếp:

• Phương pháp 1: Vẽ ba đường trung trực của tam giác. Giao điểm của ba đường này chính là tâm đường tròn ngoại tiếp.

• Phương pháp 2: Sử dụng tính chất khoảng cách từ tâm đến ba đỉnh bằng nhau. Gọi tâm đường tròn ngoại tiếp là I(x, y), ta có IA = IB = IC. Từ đó, ta thiết lập hệ phương trình và giải để tìm tọa độ của I.

Ví dụ, cho tam giác ABC với A(1; 2), B(3; 4), C(5; 0). Để tìm tâm I(x, y) của đường tròn ngoại tiếp, ta giải hệ phương trình:

(x - 1)^2 + (y - 2)^2 = (x - 3)^2 + (y - 4)^2
(x - 1)^2 + (y - 2)^2 = (x - 5)^2 + (y - 0)^2

Giải hệ phương trình này, ta sẽ tìm được tọa độ của tâm I.

4. Ứng Dụng Của Tâm Đường Tròn Ngoại Tiếp Tam Giác Trong Giải Toán

Tâm đường tròn ngoại tiếp tam giác được ứng dụng như thế nào trong giải toán?

• Bài toán chứng minh: Tâm đường tròn ngoại tiếp được sử dụng để chứng minh các tính chất hình học, chẳng hạn như chứng minh các điểm cùng thuộc một đường tròn.

• Bài toán quỹ tích: Tìm quỹ tích của tâm đường tròn ngoại tiếp khi các đỉnh của tam giác di động theo một quy luật nào đó.

• Bài toán dựng hình: Dựng đường tròn ngoại tiếp khi biết các yếu tố của tam giác.

• Bài toán tính toán: Tính bán kính đường tròn ngoại tiếp, diện tích tam giác, hoặc các yếu tố khác liên quan đến tam giác.

Theo kinh nghiệm của nhiều giáo viên toán, việc nắm vững ứng dụng của tâm đường tròn ngoại tiếp giúp học sinh tự tin hơn khi giải các bài toán hình học (Phạm Thị Bình, 2020).

Ví dụ, để chứng minh bốn điểm cùng thuộc một đường tròn, ta có thể chứng minh tâm đường tròn ngoại tiếp của một tam giác tạo bởi ba trong bốn điểm đó cách đều điểm còn lại.

5. Các Dạng Bài Tập Về Tâm Đường Tròn Ngoại Tiếp Tam Giác

Những dạng bài tập thường gặp liên quan đến tâm đường tròn ngoại tiếp tam giác là gì?

• Dạng 1: Xác định tâm và bán kính đường tròn ngoại tiếp khi biết tọa độ các đỉnh của tam giác.

• Dạng 2: Chứng minh một điểm là tâm đường tròn ngoại tiếp của tam giác.

• Dạng 3: Tính các yếu tố liên quan đến đường tròn ngoại tiếp (bán kính, diện tích, độ dài cung…).

• Dạng 4: Tìm quỹ tích của tâm đường tròn ngoại tiếp khi các đỉnh của tam giác di động.

• Dạng 5: Ứng dụng tâm đường tròn ngoại tiếp để giải các bài toán thực tế (ví dụ: xác định vị trí đặt trạm phát sóng để phủ sóng đều ba khu dân cư).

tic.edu.vn cung cấp rất nhiều bài tập có lời giải chi tiết về các dạng này, giúp bạn luyện tập và nâng cao kỹ năng giải toán.

Ví dụ, một bài tập điển hình là cho tam giác ABC với A(1; 1), B(4; 5), C(5; -2). Hãy tìm tọa độ tâm và bán kính đường tròn ngoại tiếp tam giác ABC.

6. Mối Liên Hệ Giữa Tâm Đường Tròn Ngoại Tiếp Và Các Yếu Tố Khác Của Tam Giác

Tâm đường tròn ngoại tiếp có mối liên hệ như thế nào với các yếu tố khác của tam giác?

• Đường trung trực: Tâm đường tròn ngoại tiếp là giao điểm của ba đường trung trực.

• Đường trung tuyến: Trong tam giác đều, tâm đường tròn ngoại tiếp trùng với trọng tâm (giao điểm của ba đường trung tuyến).

• Đường cao: Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.

• Đường phân giác: Tâm đường tròn nội tiếp (giao điểm của ba đường phân giác) không trùng với tâm đường tròn ngoại tiếp, trừ trường hợp tam giác đều.

Theo một nghiên cứu của trường Đại học Khoa học Tự nhiên TP.HCM, việc hiểu rõ mối liên hệ giữa tâm đường tròn ngoại tiếp và các yếu tố khác của tam giác giúp học sinh có cái nhìn tổng quan và sâu sắc hơn về hình học (Trần Văn An, 2019).

Ví dụ, biết tâm đường tròn ngoại tiếp trùng với trọng tâm, ta có thể suy ra tam giác đó là tam giác đều.

7. Công Thức Tính Bán Kính Đường Tròn Ngoại Tiếp Tam Giác

Làm thế nào để tính bán kính của đường tròn ngoại tiếp tam giác?

Có ba công thức phổ biến để tính bán kính R của đường tròn ngoại tiếp tam giác ABC:

• Công thức 1: R = a / (2sinA) = b / (2sinB) = c / (2sinC), trong đó a, b, c là độ dài các cạnh và A, B, C là các góc đối diện.

• Công thức 2: R = (abc) / (4S), trong đó S là diện tích của tam giác.

• Công thức 3: Trong tam giác vuông, R = c / 2, trong đó c là độ dài cạnh huyền.

Ví dụ, cho tam giác ABC có a = 5, b = 7, c = 8. Sử dụng công thức Heron để tính diện tích S, sau đó áp dụng công thức R = (abc) / (4S) để tính bán kính đường tròn ngoại tiếp.

8. Tâm Đường Tròn Ngoại Tiếp Tam Giác Trong Các Trường Hợp Đặc Biệt

Vị trí của tâm đường tròn ngoại tiếp có gì đặc biệt trong các loại tam giác đặc biệt?

• Tam giác đều: Tâm đường tròn ngoại tiếp trùng với trọng tâm, trực tâm và tâm đường tròn nội tiếp.

• Tam giác vuông: Tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.

• Tam giác cân: Tâm đường tròn ngoại tiếp nằm trên đường trung trực của cạnh đáy.

• Tam giác tù: Tâm đường tròn ngoại tiếp nằm bên ngoài tam giác.

Việc nhận biết vị trí tâm đường tròn ngoại tiếp trong các trường hợp đặc biệt giúp giải toán nhanh hơn và chính xác hơn.

Ví dụ, nếu bạn biết một tam giác là đều, bạn có thể dễ dàng xác định tâm đường tròn ngoại tiếp mà không cần vẽ đường trung trực.

9. Lịch Sử Và Phát Triển Của Khái Niệm Tâm Đường Tròn Ngoại Tiếp Tam Giác

Khái niệm tâm đường tròn ngoại tiếp tam giác đã hình thành và phát triển như thế nào?

Khái niệm về đường tròn ngoại tiếp và tâm của nó đã xuất hiện từ thời Hy Lạp cổ đại, gắn liền với các nhà toán học như Euclid và Archimedes. Các công trình nghiên cứu của họ đã đặt nền móng cho hình học phẳng, trong đó có đường tròn ngoại tiếp tam giác.

Trong suốt lịch sử, các nhà toán học đã không ngừng khám phá và ứng dụng các tính chất của tâm đường tròn ngoại tiếp để giải quyết các bài toán hình học phức tạp. Ngày nay, khái niệm này vẫn là một phần quan trọng trong chương trình toán học phổ thông và cao cấp.

10. FAQ – Câu Hỏi Thường Gặp Về Tâm Đường Tròn Ngoại Tiếp Tam Giác

Dưới đây là một số câu hỏi thường gặp về tâm đường tròn ngoại tiếp tam giác:

Câu 1: Tâm đường tròn ngoại tiếp có luôn nằm trong tam giác không?

Không, tâm đường tròn ngoại tiếp có thể nằm trong (tam giác nhọn), trên (tam giác vuông) hoặc ngoài (tam giác tù) tam giác.

Câu 2: Làm thế nào để tìm tâm đường tròn ngoại tiếp bằng compa và thước kẻ?

Vẽ hai đường trung trực của hai cạnh bất kỳ của tam giác. Giao điểm của chúng là tâm đường tròn ngoại tiếp.

Câu 3: Tâm đường tròn ngoại tiếp có phải là duy nhất không?

Có, mỗi tam giác chỉ có một tâm đường tròn ngoại tiếp duy nhất.

Câu 4: Tâm đường tròn ngoại tiếp có liên quan gì đến diện tích tam giác?

Có, bán kính đường tròn ngoại tiếp có thể được tính bằng công thức R = (abc) / (4S), trong đó S là diện tích tam giác.

Câu 5: Trong tam giác vuông, tâm đường tròn ngoại tiếp nằm ở đâu?

Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền.

Câu 6: Làm thế nào để viết phương trình đường tròn ngoại tiếp tam giác?

Tìm tọa độ tâm I(x, y) và bán kính R. Sau đó, viết phương trình đường tròn có dạng (x – a)^2 + (y – b)^2 = R^2.

Câu 7: Tâm đường tròn ngoại tiếp có ứng dụng gì trong thực tế?

Ứng dụng trong việc xác định vị trí tối ưu để đặt các thiết bị phủ sóng (ví dụ: trạm phát sóng điện thoại) sao cho khoảng cách đến các khu vực cần phủ sóng là bằng nhau.

Câu 8: Có phải mọi tứ giác đều có đường tròn ngoại tiếp không?

Không, chỉ những tứ giác nội tiếp (tổng hai góc đối bằng 180 độ) mới có đường tròn ngoại tiếp.

Câu 9: Tâm đường tròn ngoại tiếp có trùng với trọng tâm của tam giác không?

Chỉ trong tam giác đều, tâm đường tròn ngoại tiếp mới trùng với trọng tâm.

Câu 10: Nếu biết tọa độ ba đỉnh của tam giác, làm thế nào để tìm tọa độ tâm đường tròn ngoại tiếp?

Giải hệ phương trình IA = IB = IC, trong đó I(x, y) là tâm đường tròn ngoại tiếp.

Hy vọng bài viết này đã cung cấp cho bạn đầy đủ kiến thức về tâm đường tròn ngoại tiếp tam giác. Để khám phá thêm nhiều tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, hãy truy cập tic.edu.vn ngay hôm nay.

tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên hành trình chinh phục tri thức. Nếu bạn gặp bất kỳ khó khăn nào trong quá trình học tập, đừng ngần ngại liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ kịp thời.