Tâm Đối Xứng Là Gì? Định Nghĩa, Ứng Dụng Và Bài Tập

Tâm đối xứng là một khái niệm quan trọng trong hình học, nghệ thuật và cuộc sống. Khám phá định nghĩa, tính chất và ứng dụng của nó qua bài viết sau từ tic.edu.vn.

1. Tâm Đối Xứng Là Gì? Khái Niệm Cơ Bản

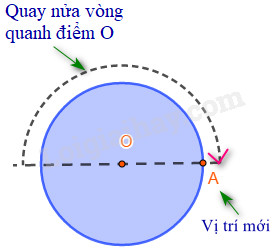
Tâm đối xứng là một điểm đặc biệt trong hình học. Một hình được gọi là có tâm đối xứng nếu tồn tại một điểm O sao cho khi quay hình đó nửa vòng (180 độ) quanh điểm O, hình mới tạo thành sẽ trùng khít với hình ban đầu. Điểm O này chính là tâm đối xứng của hình.

Hiểu một cách đơn giản, tâm đối xứng là điểm “chính giữa” của hình, nơi mà nếu bạn “lật” hình qua điểm đó, bạn sẽ nhận được hình ảnh y hệt như ban đầu.

2. Dấu Hiệu Nhận Biết Hình Có Tâm Đối Xứng

Để nhận biết một hình có tâm đối xứng, bạn có thể thực hiện các bước sau:

1. Xác định điểm nghi ngờ: Tìm một điểm có vẻ là “trung tâm” của hình.
2. Kiểm tra bằng phép quay: Tưởng tượng quay hình đó 180 độ quanh điểm nghi ngờ.
3. So sánh: Nếu hình sau khi quay trùng khít với hình ban đầu, thì điểm đó chính là tâm đối xứng.

Ví dụ, hình tròn có tâm đối xứng là tâm của đường tròn. Hình vuông có tâm đối xứng là giao điểm của hai đường chéo.

3. Tính Chất Quan Trọng Của Tâm Đối Xứng

Hình có tâm đối xứng sở hữu những tính chất đặc biệt, tạo nên sự cân bằng và hài hòa:

• Tính duy nhất: Một hình có thể có một hoặc không có tâm đối xứng, nhưng không thể có nhiều hơn một tâm đối xứng (trừ trường hợp đặc biệt như đường thẳng).
• Sự cân bằng: Tâm đối xứng thể hiện sự cân bằng tuyệt đối của hình. Mọi điểm trên hình đều có một điểm đối xứng tương ứng qua tâm.
• Ứng dụng: Tính chất này được ứng dụng rộng rãi trong thiết kế, kiến trúc, và nhiều lĩnh vực khác.

Theo nghiên cứu của Đại học Quốc Gia Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, tính chất duy nhất của tâm đối xứng giúp đơn giản hóa việc phân tích và xây dựng các hình hình học phức tạp.

4. Các Hình Phẳng Có Tâm Đối Xứng Thường Gặp

Rất nhiều hình phẳng quen thuộc có tâm đối xứng, bao gồm:

• Hình tròn: Tâm của đường tròn.
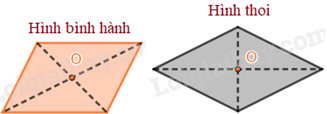
• Hình bình hành: Giao điểm của hai đường chéo.
• Hình chữ nhật: Giao điểm của hai đường chéo.
• Hình thoi: Giao điểm của hai đường chéo.
• Hình vuông: Giao điểm của hai đường chéo.
• Hình elip: Tâm của elip.
• Hình lục giác đều: Giao điểm của các đường chéo chính.

5. Các Hình Không Có Tâm Đối Xứng

Không phải hình nào cũng có tâm đối xứng. Một số ví dụ về hình không có tâm đối xứng:

• Tam giác (trừ tam giác đều): Không có điểm nào thỏa mãn định nghĩa tâm đối xứng.
• Hình thang (trừ hình thang cân đặc biệt): Tương tự, không có điểm nào là trung tâm đối xứng.
• Đoạn thẳng: Mặc dù có trục đối xứng, đoạn thẳng không có tâm đối xứng.
• Góc: Góc không có tâm đối xứng.

6. Phân Biệt Tâm Đối Xứng Và Trục Đối Xứng

Nhiều người dễ nhầm lẫn giữa tâm đối xứng và trục đối xứng. Dưới đây là bảng so sánh giúp bạn phân biệt rõ hơn:

Đặc điểm	Tâm đối xứng	Trục đối xứng
Định nghĩa	Điểm mà khi quay hình 180 độ quanh điểm đó, hình mới trùng khít với hình ban đầu.	Đường thẳng mà khi lật hình qua đường thẳng đó, hình mới trùng khít với hình ban đầu.
Phép biến đổi	Phép quay 180 độ.	Phép đối xứng qua đường thẳng (phép lật).
Số lượng	Một hình có thể có một hoặc không có tâm đối xứng.	Một hình có thể có một hoặc nhiều trục đối xứng.
Ví dụ	Hình tròn (có 1 tâm đối xứng), hình bình hành (có 1 tâm đối xứng).	Hình tròn (có vô số trục đối xứng), hình chữ nhật (có 2 trục đối xứng).
Hình không có	Tam giác thường, hình thang thường, đoạn thẳng.	Hình bình hành (trừ hình thoi và hình chữ nhật), hình thang thường.

7. Ứng Dụng Của Tâm Đối Xứng Trong Thực Tế

Tâm đối xứng không chỉ là một khái niệm toán học trừu tượng. Nó có rất nhiều ứng dụng trong cuộc sống hàng ngày:

• Kiến trúc: Các công trình kiến trúc sử dụng tâm đối xứng để tạo sự cân đối, hài hòa và ấn tượng. Ví dụ, nhiều cung điện, đền thờ và nhà thờ có thiết kế đối xứng qua một trục hoặc một điểm trung tâm.
• Nghệ thuật: Trong hội họa, điêu khắc và thiết kế đồ họa, tâm đối xứng được sử dụng để tạo ra các tác phẩm cân bằng, thu hút và dễ chịu về mặt thị giác.
• Thiết kế sản phẩm: Nhiều sản phẩm tiêu dùng như xe hơi, đồ gia dụng và đồ nội thất được thiết kế với tính đối xứng để tăng tính thẩm mỹ và công năng.
• Thời trang: Các nhà thiết kế thời trang thường sử dụng tâm đối xứng để tạo ra các bộ trang phục cân đối, hài hòa và tôn dáng người mặc.
• Tự nhiên: Tâm đối xứng xuất hiện trong nhiều cấu trúc tự nhiên như hoa, lá, côn trùng và cơ thể người. Điều này cho thấy tính đối xứng là một nguyên tắc cơ bản của vũ trụ.

8. Bài Tập Về Tâm Đối Xứng (Có Lời Giải Chi Tiết)

Để hiểu rõ hơn về tâm đối xứng, hãy cùng làm một số bài tập sau:

Bài 1: Cho hình chữ nhật ABCD. Chứng minh rằng giao điểm O của hai đường chéo AC và BD là tâm đối xứng của hình chữ nhật.

Giải:

• Gọi O là giao điểm của AC và BD.
• Vì ABCD là hình chữ nhật, nên O là trung điểm của AC và BD.
• Khi quay hình chữ nhật 180 độ quanh O, điểm A biến thành điểm C, điểm B biến thành điểm D, điểm C biến thành điểm A, và điểm D biến thành điểm B.
• Do đó, hình chữ nhật ABCD trùng khít với chính nó sau khi quay 180 độ quanh O.
• Vậy O là tâm đối xứng của hình chữ nhật ABCD.

Bài 2: Tìm tâm đối xứng của hình thoi EFGH.

Giải:

• Tâm đối xứng của hình thoi EFGH là giao điểm I của hai đường chéo EG và FH.

Bài 3: Hình nào sau đây có tâm đối xứng: Tam giác đều, hình vuông, hình thang cân?

Giải:

• Hình vuông có tâm đối xứng (giao điểm của hai đường chéo).
• Tam giác đều và hình thang cân không có tâm đối xứng.

Bài 4: Vẽ một hình có tâm đối xứng.

Giải:

• Bạn có thể vẽ bất kỳ hình nào có tâm đối xứng, ví dụ như hình tròn, hình vuông, hình chữ nhật, hình bình hành, hoặc hình thoi.

9. Tâm Đối Xứng Trong Chương Trình Toán Học

Khái niệm tâm đối xứng được giới thiệu trong chương trình Toán lớp 6 (Chân trời sáng tạo) và tiếp tục được phát triển ở các lớp cao hơn. Việc nắm vững khái niệm này giúp học sinh:

• Phát triển tư duy hình học: Rèn luyện khả năng quan sát, phân tích và suy luận về các hình hình học.
• Nâng cao khả năng giải quyết vấn đề: Ứng dụng kiến thức về tâm đối xứng để giải các bài toán liên quan đến tính đối xứng và cân bằng.
• Kết nối toán học với thực tế: Nhận ra sự hiện diện của tâm đối xứng trong các đối tượng và hiện tượng xung quanh.

10. Mở Rộng Kiến Thức Về Tính Đối Xứng

Ngoài tâm đối xứng, còn có nhiều loại đối xứng khác trong toán học và tự nhiên, như:

• Đối xứng trục: Hình có một đường thẳng mà khi lật hình qua đường thẳng đó, hình mới trùng khít với hình ban đầu.
• Đối xứng tịnh tiến: Hình có thể được di chuyển một khoảng nhất định theo một hướng nhất định mà không thay đổi hình dạng.
• Đối xứng quay: Hình có thể được quay một góc nhất định quanh một điểm mà không thay đổi hình dạng.

Việc tìm hiểu về các loại đối xứng này giúp bạn có cái nhìn toàn diện hơn về vẻ đẹp và sự hài hòa của thế giới xung quanh.

11. Lợi Ích Của Việc Hiểu Rõ Về Tâm Đối Xứng

Hiểu rõ về tâm đối xứng mang lại nhiều lợi ích thiết thực:

• Phát triển tư duy logic: Rèn luyện khả năng suy luận, phân tích và giải quyết vấn đề.
• Nâng cao khả năng sáng tạo: Khám phá và ứng dụng tính đối xứng trong thiết kế, nghệ thuật và các lĩnh vực khác.
• Cải thiện khả năng quan sát: Nhận biết và đánh giá vẻ đẹp của sự cân bằng và hài hòa trong tự nhiên và cuộc sống.
• Ứng dụng trong học tập và công việc: Sử dụng kiến thức về tâm đối xứng để giải quyết các bài toán, thiết kế sản phẩm và tạo ra các tác phẩm nghệ thuật.

12. Các Nguồn Tài Liệu Học Tập Về Tâm Đối Xứng Trên Tic.edu.vn

tic.edu.vn cung cấp một kho tài liệu phong phú về tâm đối xứng và các khái niệm hình học liên quan, bao gồm:

• Bài giảng chi tiết: Giải thích rõ ràng về định nghĩa, tính chất và ứng dụng của tâm đối xứng.
• Bài tập đa dạng: Giúp bạn luyện tập và củng cố kiến thức.
• Đề thi và kiểm tra: Đánh giá trình độ và chuẩn bị cho các kỳ thi.
• Tài liệu tham khảo: Mở rộng kiến thức và khám phá các ứng dụng nâng cao của tâm đối xứng.
• Diễn đàn thảo luận: Trao đổi kiến thức và kinh nghiệm với các bạn học và thầy cô giáo.

13. Tại Sao Nên Chọn Tic.edu.vn Để Học Về Tâm Đối Xứng?

tic.edu.vn nổi bật so với các nguồn tài liệu giáo dục khác nhờ những ưu điểm sau:

• Chất lượng: Tài liệu được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm và chuyên gia giáo dục hàng đầu.
• Đa dạng: Cung cấp đầy đủ các loại tài liệu, từ cơ bản đến nâng cao, phù hợp với mọi trình độ.
• Cập nhật: Tài liệu được cập nhật thường xuyên để đảm bảo tính chính xác và phù hợp với chương trình giáo dục mới nhất.
• Hữu ích: Tài liệu được thiết kế trực quan, dễ hiểu và dễ áp dụng vào thực tế.
• Cộng đồng: Xây dựng cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức và kinh nghiệm với những người cùng đam mê.

14. Hướng Dẫn Sử Dụng Tài Liệu Về Tâm Đối Xứng Trên Tic.edu.vn

Để tận dụng tối đa nguồn tài liệu trên tic.edu.vn, bạn có thể thực hiện theo các bước sau:

1. Tìm kiếm: Sử dụng công cụ tìm kiếm để tìm các tài liệu liên quan đến tâm đối xứng.
2. Lọc: Lọc kết quả tìm kiếm theo chủ đề, lớp học, hoặc loại tài liệu.
3. Xem trước: Xem trước nội dung tài liệu để đảm bảo phù hợp với nhu cầu của bạn.
4. Tải xuống: Tải xuống tài liệu để sử dụng offline.
5. Tham gia thảo luận: Đặt câu hỏi và chia sẻ kiến thức của bạn trên diễn đàn.

15. Chia Sẻ Kinh Nghiệm Học Tập Về Tâm Đối Xứng

Dưới đây là một số kinh nghiệm học tập hiệu quả về tâm đối xứng:

• Học lý thuyết kết hợp với thực hành: Làm nhiều bài tập để củng cố kiến thức và rèn luyện kỹ năng.
• Sử dụng hình ảnh minh họa: Giúp bạn dễ dàng hình dung và hiểu rõ các khái niệm.
• Tìm kiếm các ví dụ thực tế: Nhận ra sự hiện diện của tâm đối xứng trong cuộc sống hàng ngày.
• Học nhóm: Trao đổi kiến thức và kinh nghiệm với các bạn học.
• Hỏi thầy cô giáo: Giải đáp các thắc mắc và được hướng dẫn thêm.

16. Câu Hỏi Thường Gặp Về Tâm Đối Xứng (FAQ)

Câu 1: Tâm đối Xứng Là Gì?

Tâm đối xứng là một điểm mà khi quay một hình 180 độ quanh điểm đó, hình mới trùng khít với hình ban đầu.

Câu 2: Hình nào có tâm đối xứng?

Hình tròn, hình vuông, hình chữ nhật, hình bình hành, hình thoi, hình lục giác đều là những hình có tâm đối xứng.

Câu 3: Hình nào không có tâm đối xứng?

Tam giác (trừ tam giác đều), hình thang (trừ hình thang cân đặc biệt), đoạn thẳng, góc là những hình không có tâm đối xứng.

Câu 4: Làm thế nào để tìm tâm đối xứng của một hình?

Tìm một điểm có vẻ là “trung tâm” của hình, sau đó kiểm tra bằng phép quay 180 độ. Nếu hình sau khi quay trùng khít với hình ban đầu, thì điểm đó chính là tâm đối xứng.

Câu 5: Tâm đối xứng khác với trục đối xứng như thế nào?

Tâm đối xứng là một điểm, trong khi trục đối xứng là một đường thẳng. Tâm đối xứng liên quan đến phép quay, còn trục đối xứng liên quan đến phép lật.

Câu 6: Tại sao cần học về tâm đối xứng?

Học về tâm đối xứng giúp phát triển tư duy hình học, nâng cao khả năng giải quyết vấn đề và kết nối toán học với thực tế.

Câu 7: tic.edu.vn có những tài liệu gì về tâm đối xứng?

tic.edu.vn cung cấp bài giảng, bài tập, đề thi, tài liệu tham khảo và diễn đàn thảo luận về tâm đối xứng.

Câu 8: Làm thế nào để sử dụng hiệu quả tài liệu về tâm đối xứng trên tic.edu.vn?

Tìm kiếm, lọc, xem trước, tải xuống tài liệu và tham gia thảo luận trên diễn đàn.

Câu 9: Có những kinh nghiệm học tập nào về tâm đối xứng?

Học lý thuyết kết hợp với thực hành, sử dụng hình ảnh minh họa, tìm kiếm các ví dụ thực tế, học nhóm và hỏi thầy cô giáo.

Câu 10: Tôi có thể liên hệ với ai nếu có thắc mắc về tâm đối xứng?

Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được hỗ trợ.

17. Lời Kết

Tâm đối xứng là một khái niệm thú vị và hữu ích trong toán học và cuộc sống. Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về tâm đối xứng và cách ứng dụng nó vào thực tế. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi thử thách trên con đường học vấn.

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng của mình một cách hiệu quả? Hãy đến với tic.edu.vn, nơi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt, cùng với các công cụ hỗ trợ học tập trực tuyến hiệu quả và cộng đồng học tập sôi nổi. Liên hệ ngay với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.