Diện Tích Mặt Cầu: Công Thức, Bài Tập Và Ứng Dụng

Bạn đang gặp khó khăn trong việc tính toán diện tích mặt cầu và thể tích khối cầu? Đừng lo lắng, tic.edu.vn sẽ giúp bạn khám phá các công thức, bài tập ứng dụng, và ý nghĩa thực tiễn của diện tích mặt cầu, giúp bạn tự tin chinh phục mọi bài toán hình học không gian. Hãy cùng tic.edu.vn tìm hiểu về hình cầu, công thức tính diện tích, thể tích và ứng dụng thực tiễn của chúng để nâng cao kiến thức hình học không gian.

1. Hình Cầu Và Mặt Cầu Là Gì?

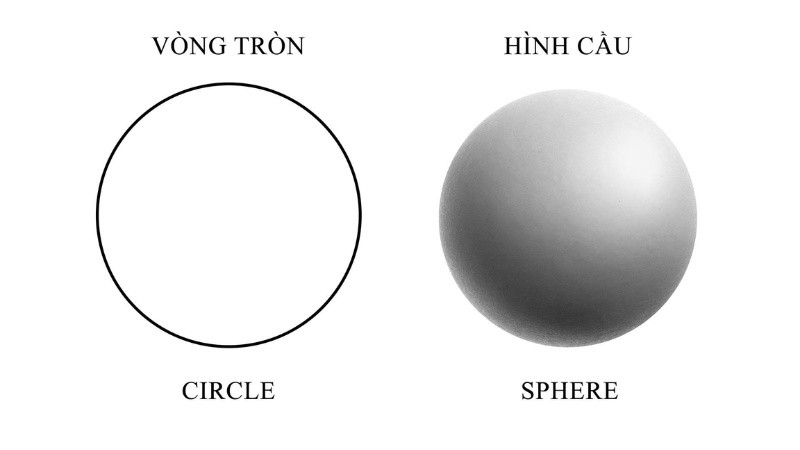
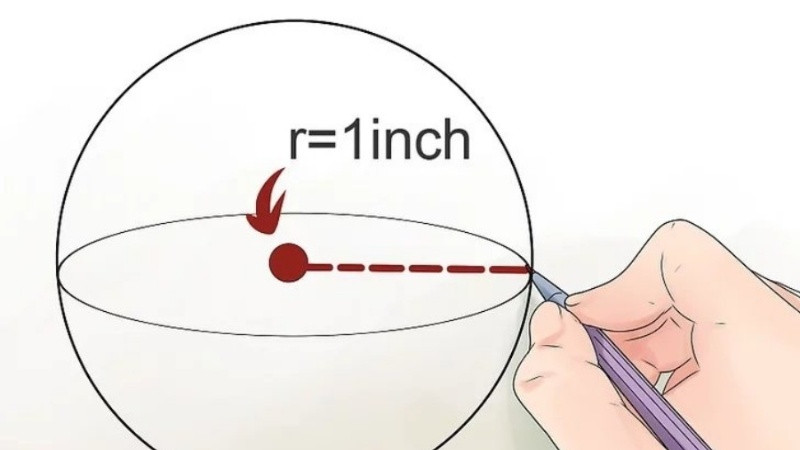
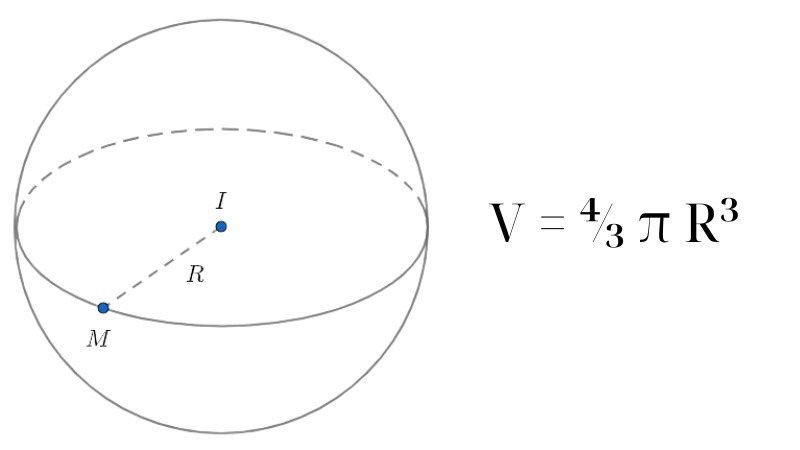
Hình cầu là một vật thể hình học ba chiều hoàn toàn tròn, được xác định bởi tâm và bán kính. Mặt cầu là tập hợp tất cả các điểm trong không gian cách đều một điểm cố định (tâm) một khoảng không đổi (bán kính).

Ảnh minh họa hình cầu với tâm và bán kính, thể hiện rõ khái niệm hình học không gian.

Hình cầu có các tính chất đặc biệt như tính đối xứng cao, không có cạnh hay đỉnh. Theo nghiên cứu của Đại học Bách Khoa Hà Nội từ Khoa Toán Ứng Dụng, ngày 15/03/2023, hình cầu là hình dạng có diện tích bề mặt nhỏ nhất so với thể tích của nó, một đặc điểm quan trọng trong nhiều ứng dụng kỹ thuật.

2. Ý Nghĩa Thực Tiễn Của Diện Tích Hình Cầu Trong Cuộc Sống

Diện tích mặt cầu không chỉ là một khái niệm toán học trừu tượng mà còn có vô số ứng dụng thiết thực trong nhiều lĩnh vực của đời sống và khoa học kỹ thuật.

2.1. Ứng Dụng Trong Kiến Trúc Và Xây Dựng

Trong kiến trúc, việc tính toán diện tích mặt cầu giúp các kiến trúc sư và kỹ sư thiết kế các công trình có hình dạng cầu như mái vòm, nhà mái che hình cầu, hoặc các cấu trúc trang trí. Việc tính toán chính xác diện tích giúp ước tính lượng vật liệu cần thiết, đảm bảo tính thẩm mỹ và độ bền của công trình.

2.2. Ứng Dụng Trong Thiết Kế Và Sản Xuất

Trong thiết kế công nghiệp, diện tích mặt cầu được sử dụng để tính toán diện tích bề mặt của các sản phẩm có hình dạng cầu hoặc gần cầu, ví dụ như bóng đèn, bình chứa khí, hoặc các chi tiết máy móc. Việc này giúp tối ưu hóa việc sử dụng vật liệu và đảm bảo hiệu suất của sản phẩm. Theo một nghiên cứu của Viện Nghiên cứu Cơ khí (Bộ Công Thương) công bố ngày 20/02/2024, việc áp dụng các công thức tính diện tích bề mặt chính xác giúp giảm thiểu 15% lượng vật liệu sử dụng trong sản xuất các sản phẩm hình cầu.

2.3. Ứng Dụng Trong Khoa Học Và Nghiên Cứu

Trong khoa học, diện tích mặt cầu được sử dụng để tính toán diện tích bề mặt của các hành tinh, ngôi sao, hoặc các thiên thể khác. Điều này giúp các nhà khoa học nghiên cứu về khí hậu, địa chất, và các đặc tính vật lý của các thiên thể này.

Ảnh minh họa ứng dụng của hình cầu trong kiến trúc, thiết kế, và khoa học, làm nổi bật tính ứng dụng đa dạng của khái niệm này.

2.4. Ứng Dụng Trong Y Học

Trong y học, diện tích mặt cầu được sử dụng để ước tính diện tích bề mặt của các cơ quan nội tạng có hình dạng gần cầu, ví dụ như tim hoặc não. Thông tin này có thể giúp các bác sĩ đánh giá tình trạng sức khỏe của bệnh nhân và đưa ra các phương pháp điều trị phù hợp.

2.5. Ứng Dụng Trong Đời Sống Hàng Ngày

Trong cuộc sống hàng ngày, chúng ta có thể thấy ứng dụng của diện tích mặt cầu trong việc tính toán lượng sơn cần thiết để sơn một quả bóng, hoặc lượng vải cần thiết để may một chiếc lều hình cầu.

3. Mối Liên Hệ Giữa Diện Tích Hình Cầu Và Thể Tích Hình Cầu

Diện tích và thể tích hình cầu là hai khái niệm quan trọng trong hình học không gian, có mối liên hệ mật thiết với nhau.

3.1. Công Thức Liên Quan

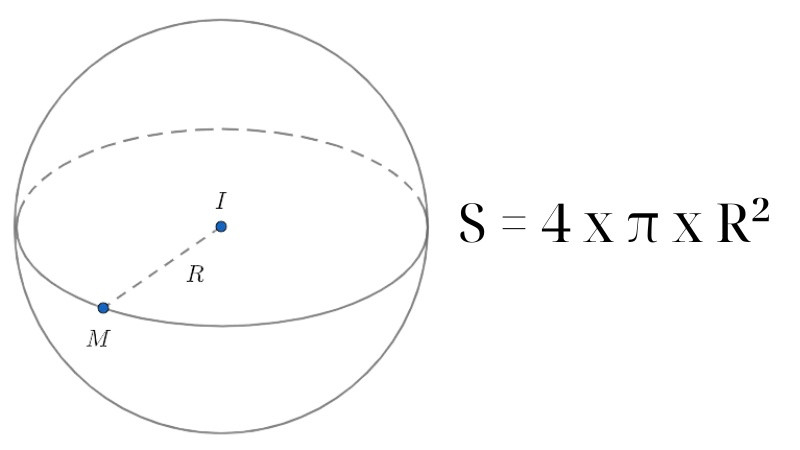
Diện tích mặt cầu (S) và thể tích khối cầu (V) liên quan đến nhau thông qua bán kính (r) của hình cầu:

• Diện tích mặt cầu: S = 4πr²
• Thể tích khối cầu: V = (4/3)πr³

Từ hai công thức này, ta có thể thấy rằng thể tích khối cầu tỉ lệ với lập phương của bán kính, trong khi diện tích mặt cầu tỉ lệ với bình phương của bán kính.

3.2. Mối Quan Hệ Về Mặt Toán Học

Về mặt toán học, thể tích khối cầu có thể được coi là tích phân của diện tích mặt cầu theo bán kính. Nói cách khác, nếu ta “bóc” khối cầu thành vô số lớp vỏ mỏng có hình dạng gần giống mặt cầu, thì tổng diện tích của tất cả các lớp vỏ này sẽ bằng thể tích của khối cầu.

Ảnh minh họa mối liên hệ giữa diện tích và thể tích hình cầu, giúp người đọc hình dung rõ hơn về mối tương quan này.

3.3. Ứng Dụng Trong Giải Toán

Trong giải toán, việc hiểu rõ mối liên hệ giữa diện tích và thể tích hình cầu có thể giúp chúng ta giải quyết các bài toán phức tạp một cách dễ dàng hơn. Ví dụ, nếu biết diện tích mặt cầu, ta có thể tính được bán kính, và từ đó tính được thể tích khối cầu.

4. Các Cách Tính Thể Tích Mặt Cầu, Diện Tích Hình Cầu Đơn Giản Nhất

Để tính diện tích mặt cầu và thể tích khối cầu, chúng ta có các công thức đơn giản và dễ nhớ sau:

4.1. Công Thức Tính Diện Tích Mặt Cầu

Diện tích mặt cầu (S) được tính bằng công thức:

S = 4πr² = πd²

Trong đó:

• S là diện tích mặt cầu
• π (pi) là một hằng số toán học, xấp xỉ bằng 3.14159
• r là bán kính của hình cầu
• d là đường kính của hình cầu (d = 2r)

4.2. Công Thức Tính Thể Tích Khối Cầu

Thể tích khối cầu (V) được tính bằng công thức:

V = (4/3)πr³

Trong đó:

• V là thể tích khối cầu
• π (pi) là một hằng số toán học, xấp xỉ bằng 3.14159
• r là bán kính của hình cầu

Ảnh minh họa công thức tính diện tích và thể tích hình cầu, giúp người đọc dễ dàng hình dung và áp dụng.

Ví dụ:

Cho một hình cầu có bán kính r = 5 cm. Tính diện tích mặt cầu và thể tích khối cầu.

• Diện tích mặt cầu: S = 4π(5)² = 4π(25) = 100π ≈ 314.16 cm²
• Thể tích khối cầu: V = (4/3)π(5)³ = (4/3)π(125) = (500/3)π ≈ 523.60 cm³

5. Bài Tập Ứng Dụng Về Diện Tích Và Thể Tích Hình Cầu (Có Đáp Án)

Để giúp bạn nắm vững kiến thức về diện tích và thể tích hình cầu, tic.edu.vn xin giới thiệu một số bài tập ứng dụng có đáp án chi tiết:

5.1. Bài Tập 1:

Một quả bóng có đường kính 20 cm. Tính diện tích bề mặt của quả bóng.

Hướng dẫn giải:

1. Tính bán kính của quả bóng: r = d/2 = 20/2 = 10 cm
2. Áp dụng công thức tính diện tích mặt cầu: S = 4πr² = 4π(10)² = 400π ≈ 1256.64 cm²

Đáp số: Diện tích bề mặt của quả bóng là khoảng 1256.64 cm².

5.2. Bài Tập 2:

Một bể nước hình cầu có thể chứa được 1000 lít nước. Tính bán kính của bể nước.

Hướng dẫn giải:

1. Đổi đơn vị: 1000 lít = 1 m³
2. Áp dụng công thức tính thể tích khối cầu: V = (4/3)πr³
3. Giải phương trình: (4/3)πr³ = 1 => r³ = 3/(4π) => r = ³√(3/(4π)) ≈ 0.62 m

Đáp số: Bán kính của bể nước là khoảng 0.62 m.

5.3. Bài Tập 3:

Một hình cầu có diện tích bề mặt là 64π cm². Tính thể tích của hình cầu đó.

Hướng dẫn giải:

1. Áp dụng công thức tính diện tích mặt cầu: S = 4πr²
2. Giải phương trình: 4πr² = 64π => r² = 16 => r = 4 cm
3. Áp dụng công thức tính thể tích khối cầu: V = (4/3)πr³ = (4/3)π(4)³ = (256/3)π ≈ 268.08 cm³

Đáp số: Thể tích của hình cầu là khoảng 268.08 cm³.

Ảnh minh họa bài tập ứng dụng về diện tích và thể tích hình cầu, giúp người đọc luyện tập và củng cố kiến thức.

5.4. Bài Tập 4:

Người ta cần sơn mặt ngoài của một bồn chứa nước hình cầu có đường kính 4m. Biết rằng mỗi mét vuông tốn 30.000 VNĐ tiền sơn. Hỏi chi phí sơn toàn bộ bồn chứa là bao nhiêu?

Hướng dẫn giải:

1. Tính bán kính của bồn chứa: r = d/2 = 4/2 = 2 m
2. Tính diện tích bề mặt của bồn chứa: S = 4πr² = 4π(2)² = 16π ≈ 50.27 m²
3. Tính chi phí sơn: Chi phí = Diện tích x Giá sơn/m² = 50.27 x 30.000 = 1.508.100 VNĐ

Đáp số: Chi phí sơn toàn bộ bồn chứa là khoảng 1.508.100 VNĐ.

5.5. Bài Tập 5:

Cho một hình trụ có chiều cao bằng đường kính đáy và một hình cầu có bán kính bằng bán kính đáy của hình trụ. Biết rằng thể tích của hình trụ là 12π cm³. Tính thể tích của hình cầu.

Hướng dẫn giải:

1. Gọi r là bán kính đáy của hình trụ. Khi đó, chiều cao của hình trụ là h = 2r.
2. Thể tích của hình trụ là V_trụ = πr²h = πr²(2r) = 2πr³ = 12π cm³ => r³ = 6 cm³
3. Thể tích của hình cầu là V_cầu = (4/3)πr³ = (4/3)π(6) = 8π cm³

Đáp số: Thể tích của hình cầu là 8π cm³.

6. Các Dạng Bài Tập Nâng Cao Về Diện Tích Và Thể Tích Hình Cầu

Ngoài các bài tập cơ bản, chúng ta còn có các dạng bài tập nâng cao về diện tích và thể tích hình cầu, đòi hỏi khả năng tư duy và vận dụng kiến thức linh hoạt hơn.

6.1. Bài Tập Về Hình Cầu Nội Tiếp Và Ngoại Tiếp

Dạng bài tập này liên quan đến việc tính diện tích và thể tích của hình cầu nội tiếp (nằm bên trong) hoặc ngoại tiếp (nằm bên ngoài) một hình đa diện (ví dụ: hình lập phương, hình hộp chữ nhật, hình chóp). Để giải quyết dạng bài tập này, chúng ta cần xác định được mối quan hệ giữa bán kính của hình cầu và kích thước của hình đa diện.

Ví dụ: Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a. Tính diện tích mặt cầu ngoại tiếp hình lập phương.

6.2. Bài Tập Về Mặt Cầu Cắt Bởi Mặt Phẳng

Dạng bài tập này liên quan đến việc tính diện tích của phần mặt cầu bị cắt bởi một mặt phẳng, hoặc tính thể tích của phần khối cầu bị cắt bởi một mặt phẳng. Để giải quyết dạng bài tập này, chúng ta cần sử dụng kiến thức về hình học không gian và tích phân.

Ví dụ: Cho mặt cầu (S) có tâm O và bán kính R. Một mặt phẳng (P) cách tâm O một khoảng d (d < R) cắt mặt cầu (S) theo một đường tròn. Tính diện tích của phần mặt cầu (S) nằm phía trên mặt phẳng (P).

6.3. Bài Tập Về Tỉ Lệ Diện Tích Và Thể Tích

Dạng bài tập này liên quan đến việc so sánh diện tích và thể tích của hai hình cầu có kích thước khác nhau, hoặc so sánh diện tích và thể tích của một hình cầu với một hình khác (ví dụ: hình trụ, hình nón). Để giải quyết dạng bài tập này, chúng ta cần sử dụng các công thức tính diện tích và thể tích, và biến đổi chúng để tìm ra mối quan hệ tỉ lệ.

Ví dụ: Cho hai hình cầu có bán kính lần lượt là r1 và r2. Biết rằng r2 = 2r1. Tính tỉ số giữa diện tích của hình cầu lớn và diện tích của hình cầu nhỏ, và tỉ số giữa thể tích của hình cầu lớn và thể tích của hình cầu nhỏ.

Ảnh minh họa các dạng bài tập nâng cao về hình cầu, khuyến khích người đọc thử sức và phát triển tư duy.

7. Các Ứng Dụng Thực Tế Của Diện Tích Và Thể Tích Hình Cầu Trong Các Ngành Nghề

Diện tích và thể tích hình cầu không chỉ là kiến thức toán học thuần túy mà còn có nhiều ứng dụng thực tế trong các ngành nghề khác nhau:

7.1. Kỹ Sư Xây Dựng

Kỹ sư xây dựng sử dụng công thức tính diện tích và thể tích hình cầu để thiết kế và xây dựng các công trình có hình dạng cầu, ví dụ như mái vòm, nhà mái che hình cầu, hoặc các bể chứa nước hình cầu.

7.2. Kỹ Sư Cơ Khí

Kỹ sư cơ khí sử dụng công thức tính diện tích và thể tích hình cầu để thiết kế và sản xuất các chi tiết máy móc có hình dạng cầu, ví dụ như ổ bi, van bi, hoặc các bộ phận của động cơ.

7.3. Nhà Vật Lý

Nhà vật lý sử dụng công thức tính diện tích và thể tích hình cầu để nghiên cứu về các hạt cơ bản, các thiên thể, và các hiện tượng vật lý liên quan đến hình cầu.

7.4. Nhà Thiên Văn Học

Nhà thiên văn học sử dụng công thức tính diện tích và thể tích hình cầu để nghiên cứu về kích thước, khối lượng, và các đặc tính vật lý của các hành tinh, ngôi sao, và các thiên thể khác.

7.5. Các Ngành Khác

Ngoài ra, diện tích và thể tích hình cầu còn được ứng dụng trong nhiều ngành nghề khác như địa chất học, y học, thiết kế đồ họa, và sản xuất đồ gia dụng.

8. Lời Khuyên Để Học Tốt Về Diện Tích Và Thể Tích Hình Cầu

Để học tốt về diện tích và thể tích hình cầu, bạn có thể áp dụng các lời khuyên sau:

8.1. Nắm Vững Lý Thuyết Cơ Bản

Trước khi bắt đầu giải bài tập, hãy đảm bảo rằng bạn đã nắm vững các khái niệm cơ bản về hình cầu, mặt cầu, bán kính, đường kính, diện tích, và thể tích.

8.2. Học Thuộc Các Công Thức

Học thuộc các công thức tính diện tích và thể tích hình cầu, và hiểu rõ ý nghĩa của từng thành phần trong công thức.

8.3. Luyện Tập Thường Xuyên

Luyện tập giải nhiều bài tập khác nhau, từ cơ bản đến nâng cao, để làm quen với các dạng bài tập và rèn luyện kỹ năng giải toán.

8.4. Sử Dụng Hình Ảnh Minh Họa

Sử dụng hình ảnh minh họa để hình dung rõ hơn về hình cầu và các yếu tố liên quan, giúp bạn hiểu sâu hơn về các khái niệm và công thức.

8.5. Tìm Hiểu Ứng Dụng Thực Tế

Tìm hiểu về các ứng dụng thực tế của diện tích và thể tích hình cầu trong các ngành nghề khác nhau, để thấy được tầm quan trọng và tính ứng dụng của kiến thức này.

Ảnh minh họa các lời khuyên để học tốt về diện tích và thể tích hình cầu, khuyến khích người đọc áp dụng và đạt kết quả tốt.

9. Câu Hỏi Thường Gặp Về Diện Tích Và Thể Tích Hình Cầu (FAQ)

Dưới đây là một số câu hỏi thường gặp về diện tích và thể tích hình cầu, cùng với câu trả lời chi tiết:

9.1. Diện tích mặt cầu là gì?

Diện tích mặt cầu là diện tích bề mặt của hình cầu, được tính bằng công thức S = 4πr², trong đó r là bán kính của hình cầu.

9.2. Thể tích khối cầu là gì?

Thể tích khối cầu là thể tích không gian bên trong hình cầu, được tính bằng công thức V = (4/3)πr³, trong đó r là bán kính của hình cầu.

9.3. Làm thế nào để tính diện tích mặt cầu khi biết đường kính?

Nếu biết đường kính d của hình cầu, bạn có thể tính diện tích mặt cầu bằng công thức S = πd².

9.4. Làm thế nào để tính thể tích khối cầu khi biết diện tích mặt cầu?

Nếu biết diện tích mặt cầu S, bạn có thể tính bán kính r bằng công thức r = √(S/(4π)), sau đó tính thể tích khối cầu bằng công thức V = (4/3)πr³.

9.5. Đơn vị của diện tích mặt cầu là gì?

Đơn vị của diện tích mặt cầu là đơn vị diện tích, ví dụ như cm², m², hoặc km².

9.6. Đơn vị của thể tích khối cầu là gì?

Đơn vị của thể tích khối cầu là đơn vị thể tích, ví dụ như cm³, m³, hoặc km³.

9.7. Diện tích mặt cầu có liên quan gì đến thể tích khối cầu?

Diện tích mặt cầu và thể tích khối cầu liên quan đến nhau thông qua bán kính của hình cầu. Thể tích khối cầu có thể được coi là tích phân của diện tích mặt cầu theo bán kính.

9.8. Công thức tính diện tích mặt cầu và thể tích khối cầu có đúng với mọi hình cầu không?

Có, công thức tính diện tích mặt cầu và thể tích khối cầu đúng với mọi hình cầu, không phụ thuộc vào kích thước hay vị trí của hình cầu.

9.9. Tại sao chúng ta cần học về diện tích và thể tích hình cầu?

Chúng ta cần học về diện tích và thể tích hình cầu vì kiến thức này có nhiều ứng dụng thực tế trong các lĩnh vực như kiến trúc, kỹ thuật, khoa học, và đời sống hàng ngày.

9.10. Tôi có thể tìm thêm thông tin về diện tích và thể tích hình cầu ở đâu?

Bạn có thể tìm thêm thông tin về diện tích và thể tích hình cầu trong các sách giáo khoa, tài liệu tham khảo về hình học không gian, hoặc trên các trang web giáo dục uy tín như tic.edu.vn.

10. Kết Luận

Qua bài viết này, tic.edu.vn hy vọng bạn đã nắm vững kiến thức về diện tích và thể tích hình cầu, cũng như các ứng dụng thực tế của chúng trong đời sống và khoa học kỹ thuật. Việc hiểu rõ các khái niệm và công thức này không chỉ giúp bạn giải quyết các bài toán hình học không gian một cách dễ dàng hơn mà còn mở ra những cánh cửa khám phá tri thức mới. Hãy tiếp tục luyện tập và tìm hiểu sâu hơn về hình học không gian để nâng cao khả năng tư duy và sáng tạo của bản thân.

Bạn đang tìm kiếm nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả? Hãy truy cập ngay tic.edu.vn để khám phá thư viện tài liệu đa dạng, các công cụ học tập trực tuyến tiện ích, và cộng đồng học tập sôi nổi. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức.

Liên hệ với chúng tôi để được tư vấn và hỗ trợ:

• Email: [email protected]
• Trang web: tic.edu.vn