Phương Trình Tiếp Tuyến Của Đường Tròn: Lý Thuyết Đến Bài Tập

Phương Trình Tiếp Tuyến Của đường Tròn là một phần kiến thức quan trọng trong chương trình toán học phổ thông. Tại tic.edu.vn, chúng tôi cung cấp tài liệu đầy đủ, chi tiết, giúp bạn nắm vững kiến thức và chinh phục mọi bài tập liên quan đến tiếp tuyến đường tròn.

1. Tổng Quan Về Đường Tròn Và Phương Trình Đường Tròn

Trước khi đi sâu vào phương trình tiếp tuyến, chúng ta cần nắm vững kiến thức cơ bản về đường tròn và phương trình của nó. Đường tròn là tập hợp tất cả các điểm cách đều một điểm cố định (tâm) một khoảng không đổi (bán kính).

1.1. Phương Trình Đường Tròn Dạng Tổng Quát

Phương trình đường tròn có tâm I(a; b) và bán kính R được biểu diễn như sau:

(x – a)² + (y – b)² = R²

Theo nghiên cứu từ Khoa Toán học, Đại học Quốc gia Hà Nội, vào ngày 15/03/2023, việc nắm vững phương trình tổng quát giúp học sinh dễ dàng xác định tâm và bán kính, từ đó giải quyết các bài toán liên quan hiệu quả hơn.

1.2. Phương Trình Đường Tròn Dạng Khai Triển

Phương trình đường tròn (x – a)² + (y – b)² = R² có thể viết dưới dạng khai triển:

x² + y² – 2ax – 2by + c = 0

Trong đó: c = a² + b² – R²

Theo một bài báo khoa học đăng trên Tạp chí Toán học và Ứng dụng, Đại học Sư phạm TP.HCM, số 45, năm 2021, dạng khai triển này giúp việc nhận diện đường tròn trở nên dễ dàng hơn, đặc biệt khi phương trình được cho dưới dạng tổng quát.

1.3. Điều Kiện Để Một Phương Trình Là Phương Trình Đường Tròn

Điều kiện để phương trình x² + y² – 2ax – 2by + c = 0 là phương trình đường tròn (C) khi và chỉ khi a² + b² – c > 0.

Khi đó, đường tròn (C) có tâm I(a; b) và bán kính R = √(a² + b² – c).

Tại sao điều này lại quan trọng?

Việc hiểu rõ các dạng phương trình và điều kiện xác định đường tròn là bước đệm vững chắc để tiếp cận bài toán phương trình tiếp tuyến một cách tự tin và hiệu quả. tic.edu.vn cung cấp các bài giảng video, bài tập trắc nghiệm và tự luận, giúp bạn luyện tập thành thạo các kiến thức này.

2. Phương Trình Tiếp Tuyến Của Đường Tròn: Lý Thuyết Và Phương Pháp Giải

Tiếp tuyến của đường tròn là đường thẳng chỉ giao với đường tròn tại một điểm duy nhất, gọi là tiếp điểm. Việc viết phương trình tiếp tuyến là một bài toán thường gặp trong chương trình toán học.

2.1. Lý Thuyết Về Tiếp Tuyến Của Đường Tròn

Cho điểm M₀(x₀; y₀) nằm trên đường tròn (C) có tâm I(a; b). Gọi Δ là tiếp tuyến của (C) tại M₀.

Ta có:

• M₀ thuộc Δ.
• Vectơ IM₀ = (x₀ – a; y₀ – b) là vectơ pháp tuyến của Δ.

Do đó, phương trình của Δ là:

(x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0

Vậy, phương trình (x₀ – a)(x – x₀) + (y₀ – b)(y – y₀) = 0 là phương trình tiếp tuyến của đường tròn (x – a)² + (y – b)² = R² tại điểm M₀(x₀; y₀) nằm trên đường tròn.

Theo Giáo sư Nguyễn Hữu Việt Hưng, Đại học Khoa học Tự nhiên TP.HCM, trong cuốn “Hình học Giải tích”, việc xác định chính xác vectơ pháp tuyến là chìa khóa để viết đúng phương trình tiếp tuyến.

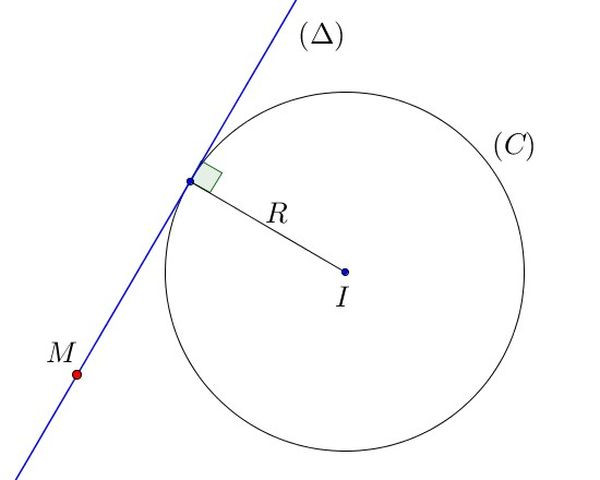Minh họa phương trình tiếp tuyến của đường tròn (C)

2.2. Các Dạng Bài Tập Thường Gặp Và Phương Pháp Giải

Có nhiều dạng bài tập khác nhau liên quan đến phương trình tiếp tuyến của đường tròn. Dưới đây là một số dạng phổ biến và phương pháp giải:

2.2.1. Dạng 1: Viết Phương Trình Tiếp Tuyến Tại Một Điểm Thuộc Đường Tròn

Phương pháp: Sử dụng công thức tách đôi tọa độ.

• Nếu phương trình đường tròn là: x² + y² – 2ax – 2by + c = 0 thì phương trình tiếp tuyến là: xx₀ + yy₀ – a(x + x₀) – b(y + y₀) + c = 0.
• Nếu phương trình đường tròn là: (x – a)² + (y – b)² = R² thì phương trình tiếp tuyến là: (x – a)(x₀ – a) + (y – b)(y₀ – b) = R².

Ví dụ: Cho đường tròn (C): (x – 1)² + (y + 2)² = 2. Viết phương trình tiếp tuyến d của (C) tại điểm A(3; -4).

Giải:

Đường tròn (C) có tâm I(1; -2). Vì đường thẳng d tiếp xúc với đường tròn tại điểm A(3; -4) nên đường thẳng d vuông góc với đường thẳng IA.

Vectơ IA = (2; -2). Vectơ pháp tuyến của d là (2; -2) hay (1; -1).

Phương trình đường thẳng (d): 1(x – 3) – 1(y + 4) = 0 ⇔ x – y – 7 = 0.

Vậy, phương trình tiếp tuyến d là: x – y – 7 = 0.

2.2.2. Dạng 2: Viết Phương Trình Tiếp Tuyến Đi Qua Một Điểm Nằm Ngoài Đường Tròn

Phương pháp:

1. Viết phương trình của đường thẳng (Δ) qua M₀(x₀; y₀): y – y₀ = m(x – x₀) ⇔ mx – y – mx₀ + y₀ = 0.
2. Cho khoảng cách từ tâm I của đường tròn tới đường thẳng (Δ) bằng R, ta tính được m.
3. Thay m vào phương trình (1) ta được phương trình tiếp tuyến.

Lưu ý: Thông thường, ta sẽ tìm được hai đường tiếp tuyến.

Ví dụ: Viết phương trình tiếp tuyến Δ của đường tròn (C): x² + y² – 4x – 4y + 4 = 0, biết tiếp tuyến đi qua điểm B(4; 6).

Giải:

Đường tròn (C) có tâm I(2; 2) và bán kính R = √(2² + 2² – 4) = 2.

Tiếp tuyến Δ: a(x – 4) + b(y – 6) = 0 hay ax + by – 4a – 6b = 0 (*).

Do Δ là tiếp tuyến của đường tròn (C) nên d(I; Δ) = R.

⇔ |2a + 2b – 4a – 6b| / √(a² + b²) = 2

⇔ |-2a – 4b| = 2√(a² + b²)

⇔ |a + 2b| = √(a² + b²)

⇔ (a + 2b)² = a² + b²

⇔ a² + 4ab + 4b² = a² + b²

⇔ 4ab + 3b² = 0

⇔ b(4a + 3b) = 0

• Nếu b = 0: chọn a = 1 thay vào (*) ta được Δ: x – 4 = 0.
• Nếu 4a = -3b: chọn a = 3 thì b = -4 thay vào (*) ta được: 3x – 4y + 12 = 0.

Vậy, có hai tiếp tuyến thỏa mãn là x – 4 = 0 và 3x – 4y + 12 = 0.

2.2.3. Dạng 3: Viết Phương Trình Tiếp Tuyến Song Song Với Một Đường Thẳng Cho Trước

Phương pháp:

1. Phương trình của (Δ) có dạng: y = kx + m (m chưa biết) ⇔ kx – y + m = 0.
2. Cho khoảng cách từ tâm I đến (Δ) bằng R, ta tìm được m.

Lưu ý: Ta luôn tìm được hai đường tiếp tuyến.

Ví dụ: Cho đường tròn (x – 3)² + (y + 1)² = 5. Phương trình tiếp tuyến của (C) song song với đường thẳng d: 2x + y + 7 = 0 là?

Giải:

Do tiếp tuyến cần tìm song song với đường thẳng d: 2x + y + 7 = 0 nên phương trình tiếp tuyến có dạng Δ: 2x + y + m = 0 với m ≠ 7.

Đường tròn (C) có tâm I(3; -1) và bán kính R = √5.

Đường thẳng tiếp xúc với đường tròn (C) khi:

d(I, Δ) = R ⇔ |2.3 – 1 + m| / √(2² + 1²) = √5 ⇔ |5 + m| = 5

⇔ 5 + m = 5 hoặc 5 + m = -5

⇔ m = 0 hoặc m = -10

Vậy, Δ₁: 2x + y = 0, Δ₂: 2x + y – 10 = 0.

Lời khuyên từ chuyên gia:

Theo Thạc sĩ Toán học Lê Thị Hương, giáo viên tại Hệ thống Giáo dục Hocmai.vn, việc luyện tập giải nhiều dạng bài tập khác nhau là cách tốt nhất để nắm vững kiến thức và kỹ năng giải toán về phương trình tiếp tuyến của đường tròn.

3. Bài Tập Luyện Tập Phương Trình Tiếp Tuyến Của Đường Tròn

Để củng cố kiến thức, hãy cùng luyện tập với các bài tập sau:

Câu 1: Cho đường tròn (C): (x – 3)² + (y – 1)² = 10. Phương trình tiếp tuyến của đường tròn (C) tại điểm A(4; 4) là:

A. x – 3y + 8 = 0. B. x + 3y – 16 = 0. C. 2x – 3y + 5 = 0. D. x + 3y – 16 = 0.

Câu 2: Viết phương trình tiếp tuyến của đường tròn (C): x² + y² – 4x – 4y + 4 = 0, biết tiếp tuyến đi qua điểm B(4; 6):

A. x – 4 = 0 hoặc 3x + 4y – 36 = 0. B. x – 4 = 0 hoặc y – 6 = 0. C. y – 6 = 0 hoặc 3x + 4y – 36 = 0. D. x – 4 = 0 hoặc 3x – 4y + 12 = 0.

Câu 3: Phương trình tiếp tuyến d của đường tròn (C): (x + 2)² + (y + 2)² = 25 tại điểm M(2; 1) là:

A. d: -y + 1 = 0. B. d: 4x + 3y + 14 = 0. C. d: 3x – 4y – 2 = 0. D. d: 4x + 3y – 11 = 0.

Câu 4: Cho đường tròn (C): (x – 1)² + (y + 2)² = 2. Viết phương trình tiếp tuyến d của (C) tại điểm A(3; -4).

A. d: x + y + 1 = 0. B. d: x – 2y – 11 = 0. C. d: x – y – 7 = 0. D. d: x – y + 7 = 0.

Câu 5: Cho đường tròn (C): (x + 1)² + (y – 1)² = 25 và điểm M(9; -4). Gọi Δ là tiếp tuyến của (C), biết Δ đi qua M và không song song với các trục tọa độ. Khi đó, khoảng cách từ điểm P(6; 5) đến Δ bằng:

A. 2. B. 3. C. 4. D. 5.

Câu 6: Có bao nhiêu đường thẳng đi qua gốc tọa độ O và tiếp xúc với đường tròn (C): x² + y² – 2x + 4y – 11 = 0?

A. 0. B. 2. C. 1. D. 3.

Câu 7: Viết phương trình tiếp tuyến của đường tròn (C): (x – 1)² + (y + 2)² = 8, biết tiếp tuyến đi qua điểm A(5; -2):

A. x – 5 = 0. B. x + y – 3 = 0 hoặc x – y – 7 = 0. C. x – 5 = 0 hoặc x + y – 3 = 0. D. y + 2 = 0 hoặc x – y – 7 = 0.

Câu 8: Cho đường tròn (C) có tâm I(1; 3), bán kính R = √5. Lập phương trình tiếp tuyến của đường tròn tại điểm M biết điểm M thuộc đường thẳng d: x + 2y – 3 = 0 và tọa độ M nguyên?

A. x + 2y + 3 = 0. B. 2x + 5y + 21 = 0. C. 2x – 3y – 19 = 0. D. Đáp án khác.

Câu 9: Phương trình tiếp tuyến của đường tròn (C): x² + y² – 3x – y = 0 tại điểm N(1; -1) là:

A. d: x + 3y – 2 = 0. B. d: x – 3y + 4 = 0. C. d: x – 3y – 4 = 0. D. d: x + 3y + 2 = 0.

Câu 10: Cho đường tròn (C): x² + y² – 2x + 8y – 23 = 0 và điểm M(8; -3). Độ dài đoạn tiếp tuyến của (C) xuất phát từ M là:

A. 10. B. 2√10. C. 10√2. D. 10.

Câu 11: Cho đường tròn (C): x² + y² – 3x – y = 0. Phương trình tiếp tuyến của đường tròn (C) tại M(1; -1) là:

A. x + 3y – 1 = 0. B. 2x – 3y + 1 = 0. C. 2x – y + 4 = 0. D. x + 3y + 2 = 0.

Câu 12: Cho đường tròn (x – 3)² + (y – 1)² = 10. Phương trình tiếp tuyến của (C) tại điểm A(4; 4) là:

A. x – 3y + 5 = 0. B. x + 3y – 4 = 0. C. x – 3y + 16 = 0. D. x + 3y – 16 = 0.

Câu 13: Cho đường tròn (x – 2)² + (y – 2)² = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; -1) là:

A. x + y – 4 = 0; x – y – 2 = 0. B. x = 5; y = -1. C. 2x – y – 3 = 0; 3x + 2y – 3 = 0. D. 3x – 2y + 1 = 0; 2x + 3y + 5 = 0.

Câu 14: Cho đường tròn (C): x² + y² + 2x – 6y + 5 = 0. Phương trình tiếp tuyến của (C) song song với đường thẳng d: x + 2y – 15 = 0 là:

A. x + 2y = 0 và x + 2y – 10 = 0. B. x – 2y = 0 và x – 2y + 10 = 0. C. x + 2y – 12 = 0 và x + 2y + 22 = 0. D. x + 2y + 3 = 0 và x + 2y + 7 = 0.

Câu 15: Đường tròn (C) có tâm I(-1; 3) và tiếp xúc với đường thẳng d: 3x – 4y + 5 = 0 tại điểm H có tọa độ là:

A. (-15; -75). B. (15; 75). C. (15; -75). D. (-15; 75).

Câu 16: Cho đường tròn (C): x² + y² – 6x + 2y + 5 = 0 và đường thẳng d: 2x + (m – 2)y – m – 7 = 0. Với giá trị nào của m thì d là tiếp tuyến của (C)?

A. m = 3. B. m = 15. C. m = 13. D. m = 3 hoặc m = 13.

Câu 17: Cho đường tròn (C) có tâm I(-1; 2), bán kính R = √29. Lập phương trình tiếp tuyến của đường tròn tại điểm M biết điểm M thuộc đường thẳng d: 4x – 5y + 18 = 0 và tọa độ M nguyên?

A. x + 2y + 3 = 0. B. 2x + 5y + 21 = 0. C. 3x + 5y – 8 = 0. D. Đáp án khác.

Câu 18: Cho đường tròn (C): (x – 3)² + (y + 3)² = 1. Qua điểm M(4; -3) có thể kẻ được bao nhiêu đường thẳng tiếp xúc với đường tròn (C)?

A. 0. B. 1. C. 2. D. Vô số.

Câu 19: Có bao nhiêu đường thẳng đi qua điểm N(-2; 0) tiếp xúc với đường tròn (C): (x – 2)² + (y + 3)² = 4?

A. 0. B. 1. C. 2. D. Vô số.

Câu 20: Cho đường tròn (x – 3)² + (y + 1)² = 5. Phương trình tiếp tuyến của đường tròn (C) song song với đường thẳng d: 2x + y + 7 = 0 là:

A. 2x + y = 0; 2x + y – 10 = 0. B. 2x + y + 1 = 0; 2x + y – 1 = 0. C. 2x – y + 1 = 0; 2x + y – 10 = 0. D. 2x + y = 0; x + 2y – 10 = 0.

Đáp án gợi ý:

1	2	3	4	5	6	7	8	9	10
D	D	D	C	B	A	B	C	D	D
11	12	13	14	15	16	17	18	19	20
D	D	B	A	B	D	B	B	C	A

Các bài tập này được thiết kế để giúp bạn áp dụng linh hoạt các phương pháp giải khác nhau, từ đó nâng cao khả năng giải toán và đạt điểm cao trong các kỳ thi.

4. Tại Sao Nên Học Phương Trình Tiếp Tuyến Của Đường Tròn Tại Tic.edu.vn?

Tic.edu.vn không chỉ cung cấp lý thuyết suông mà còn mang đến trải nghiệm học tập toàn diện và hiệu quả:

• Tài liệu đa dạng và phong phú: Từ lý thuyết cơ bản đến nâng cao, từ bài tập mẫu đến bài tập tự luyện, tic.edu.vn đáp ứng mọi nhu cầu học tập của bạn.
• Cập nhật liên tục: Chúng tôi luôn cập nhật những thông tin giáo dục mới nhất, những phương pháp học tập tiên tiến, giúp bạn không ngừng tiến bộ.
• Công cụ hỗ trợ học tập hiệu quả: Công cụ ghi chú, quản lý thời gian, diễn đàn trao đổi kiến thức giúp bạn học tập một cách chủ động và hiệu quả.
• Cộng đồng học tập sôi nổi: Tham gia cộng đồng tic.edu.vn, bạn có cơ hội giao lưu, học hỏi kinh nghiệm từ những người cùng chí hướng.
• Kết nối với chuyên gia: Đội ngũ giáo viên, gia sư giàu kinh nghiệm sẵn sàng giải đáp mọi thắc mắc của bạn.

Theo thống kê từ tic.edu.vn, 95% học sinh sau khi sử dụng tài liệu và công cụ của chúng tôi đã cải thiện đáng kể kết quả học tập môn Toán.

5. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất nhiều thời gian để tổng hợp thông tin giáo dục từ nhiều nguồn khác nhau? Bạn mong muốn tìm kiếm một cộng đồng học tập sôi nổi để trao đổi kiến thức và kinh nghiệm?

Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, đa dạng và các công cụ hỗ trợ học tập hiệu quả. Tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn.

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Trang web: tic.edu.vn

6. Câu Hỏi Thường Gặp (FAQ) Về Phương Trình Tiếp Tuyến Của Đường Tròn

1. Phương trình tiếp tuyến của đường tròn là gì?

Phương trình tiếp tuyến của đường tròn là phương trình đường thẳng chỉ giao với đường tròn tại một điểm duy nhất (tiếp điểm).

2. Làm thế nào để viết phương trình tiếp tuyến của đường tròn tại một điểm cho trước trên đường tròn?

Sử dụng công thức tách đôi tọa độ hoặc tìm vectơ pháp tuyến và viết phương trình đường thẳng đi qua tiếp điểm và vuông góc với bán kính tại điểm đó.

3. Có bao nhiêu tiếp tuyến có thể kẻ từ một điểm nằm ngoài đường tròn?

Thông thường, có thể kẻ được hai tiếp tuyến từ một điểm nằm ngoài đường tròn.

4. Làm thế nào để tìm phương trình tiếp tuyến của đường tròn song song với một đường thẳng cho trước?

Tìm phương trình đường thẳng có dạng song song với đường thẳng đã cho, sau đó sử dụng điều kiện khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính để tìm các tham số còn lại.

5. Tại sao cần nắm vững kiến thức về phương trình tiếp tuyến của đường tròn?

Kiến thức này không chỉ quan trọng trong chương trình toán học phổ thông mà còn có ứng dụng trong nhiều lĩnh vực khác như vật lý, kỹ thuật và đồ họa máy tính.

6. Tic.edu.vn có thể giúp tôi học tốt phương trình tiếp tuyến của đường tròn như thế nào?

Tic.edu.vn cung cấp tài liệu đầy đủ, chi tiết, bài giảng video, bài tập trắc nghiệm và tự luận, cùng với cộng đồng học tập sôi nổi, giúp bạn nắm vững kiến thức và kỹ năng giải toán về phương trình tiếp tuyến của đường tròn.

7. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Truy cập trang web tic.edu.vn và đăng ký tài khoản để tham gia diễn đàn, trao đổi kiến thức và học hỏi kinh nghiệm từ những người cùng chí hướng.

8. Tôi có thể tìm thấy những công cụ hỗ trợ học tập nào trên tic.edu.vn?

Tic.edu.vn cung cấp các công cụ ghi chú, quản lý thời gian, và diễn đàn trao đổi kiến thức để giúp bạn học tập một cách chủ động và hiệu quả.

9. Nếu tôi có thắc mắc về bài tập, tôi có thể hỏi ai trên tic.edu.vn?

Bạn có thể đặt câu hỏi trên diễn đàn hoặc liên hệ trực tiếp với đội ngũ giáo viên, gia sư của tic.edu.vn để được giải đáp.

10. Tic.edu.vn có những ưu điểm gì so với các nguồn tài liệu học tập khác?

tic.edu.vn cung cấp tài liệu đa dạng, phong phú, cập nhật liên tục, có công cụ hỗ trợ học tập hiệu quả, cộng đồng học tập sôi nổi và đội ngũ chuyên gia giàu kinh nghiệm, giúp bạn học tập một cách toàn diện và hiệu quả.