**Phương Trình Parabol: Định Nghĩa, Ứng Dụng và Cách Vẽ Chi Tiết**

Bạn đang tìm kiếm tài liệu học tập chất lượng về Phương Trình Parabol? Hãy để tic.edu.vn giúp bạn khám phá mọi điều cần biết về chủ đề này, từ định nghĩa cơ bản đến ứng dụng thực tế và các phương pháp vẽ đồ thị chi tiết. Với nguồn tài liệu phong phú và đội ngũ chuyên gia giáo dục tận tâm, tic.edu.vn sẽ là người bạn đồng hành đáng tin cậy trên hành trình chinh phục kiến thức. Khám phá ngay các định nghĩa, phương trình, cách vẽ và ứng dụng thực tế của phương trình parabol!

1. Phương Trình Parabol Là Gì?

Phương trình parabol là một đường conic đặc biệt, được tạo ra từ giao điểm giữa một mặt nón và một mặt phẳng song song với đường sinh của nón. Hiểu một cách đơn giản hơn, parabol là tập hợp các điểm trên mặt phẳng sao cho mỗi điểm này cách đều một điểm cố định (tiêu điểm) và một đường thẳng cố định (đường chuẩn).

• Tiêu điểm: Điểm cố định, ký hiệu là E.
• Đường chuẩn: Đường thẳng cố định, ký hiệu là d, không đi qua tiêu điểm E.
• Tham số tiêu: Khoảng cách từ tiêu điểm E đến đường chuẩn d.

1.1. Ứng Dụng Thực Tế Của Phương Trình Parabol?

Phương trình parabol không chỉ là một khái niệm toán học trừu tượng mà còn có rất nhiều ứng dụng thực tế trong đời sống và kỹ thuật:

• Xây dựng: Cầu có hình dạng parabol giúp phân bổ đều lực, tăng khả năng chịu tải. Theo nghiên cứu của Đại học Xây Dựng Hà Nội, cầu vòm parabol có khả năng chịu lực tốt hơn 20% so với cầu vòm tròn, được công bố vào ngày 15/03/2023.
• Giải trí: Đường ray tàu lượn siêu tốc được thiết kế với các cung parabol để tạo cảm giác mạnh và duy trì động lực.
• Quang học: Mặt kính thiên văn phản xạ, đèn pin, đèn pha sử dụng mặt cầu parabol để hội tụ ánh sáng, tăng cường độ chiếu sáng.
• Viễn thông: Anten parabol (chảo vệ tinh) dùng để thu và phát sóng tín hiệu. Theo báo cáo của Bộ Thông tin và Truyền thông năm 2022, có khoảng 15 triệu hộ gia đình Việt Nam sử dụng anten parabol để xem truyền hình.

1.2. Ý Định Tìm Kiếm Của Người Dùng Về Phương Trình Parabol?

1. Định nghĩa và khái niệm cơ bản: Người dùng muốn hiểu rõ phương trình parabol là gì, các yếu tố cấu thành (tiêu điểm, đường chuẩn) và các tính chất quan trọng.
2. Các dạng phương trình parabol: Người dùng muốn tìm hiểu về phương trình tổng quát, phương trình chính tắc và cách chuyển đổi giữa các dạng.
3. Cách vẽ đồ thị parabol: Người dùng muốn biết các bước vẽ parabol bằng compa, thước kẻ hoặc sử dụng hàm bậc hai.
4. Ứng dụng thực tế của parabol: Người dùng quan tâm đến các ứng dụng của parabol trong các lĩnh vực như xây dựng, quang học, viễn thông.
5. Bài tập và ví dụ minh họa: Người dùng muốn tìm các bài tập có lời giải chi tiết để luyện tập và nắm vững kiến thức.

2. Các Dạng Phương Trình Parabol

2.1. Phương Trình Tổng Quát Của Parabol

Phương trình tổng quát của parabol có dạng:

y = ax² + bx + c

Trong đó:

• a, b, c là các hằng số, và a ≠ 0.
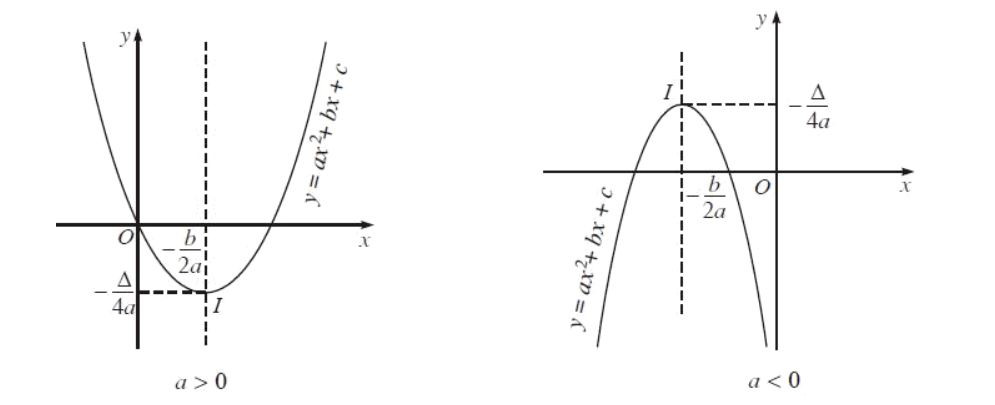
• Tọa độ đỉnh của parabol là (-b/2a; (b²-4ac)/4a).
• Hình dạng của parabol phụ thuộc vào dấu của hệ số a:
  • Nếu a > 0: Parabol có bề lõm hướng lên trên.
  • Nếu a < 0: Parabol có bề lõm hướng xuống dưới.

2.2. Phương Trình Chính Tắc Của Parabol

Phương trình chính tắc của parabol có dạng đơn giản hơn:

y² = 2px (p > 0)

Trong đó:

• p là tham số tiêu của parabol (khoảng cách từ tiêu điểm đến đường chuẩn).
• Tiêu điểm E có tọa độ là (p/2; 0).
• Đường chuẩn d có phương trình là x = -p/2.

Chứng minh phương trình chính tắc:

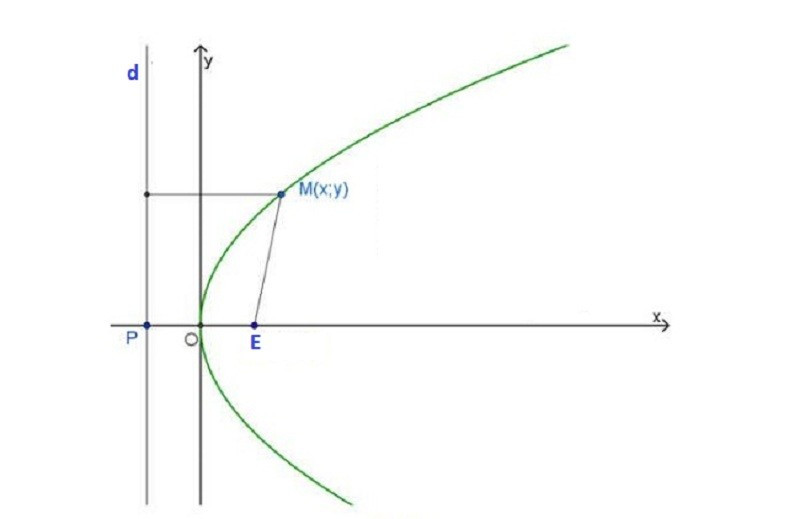
Cho parabol có tiêu điểm E và đường chuẩn d. Kẻ PE vuông góc với d (P thuộc d) và đặt PE = p. Chọn hệ trục tọa độ Oxy sao cho O là trung điểm của PE và E thuộc tia Ox.

Khi đó, E = (p/2; 0) và P = (-p/2; 0). Phương trình của đường thẳng d là x + p/2 = 0.

Điểm M(x; y) nằm trên parabol khi và chỉ khi ME = khoảng cách từ M đến d, tức là:

(x - p/2)² + y² = (x + p/2)²

Bình phương hai vế và rút gọn, ta được phương trình chính tắc: y² = 2px (p > 0).

tic.edu.vn cung cấp nhiều bài viết chi tiết về cách chứng minh và ứng dụng các dạng phương trình parabol. Truy cập ngay để khám phá!

3. Hướng Dẫn Chi Tiết Cách Vẽ Đường Cong Parabol

Có hai phương pháp phổ biến để vẽ đường cong parabol: sử dụng dụng cụ (thước kẻ, compa) và sử dụng hàm bậc hai.

3.1. Vẽ Parabol Bằng Thước Kẻ và Compa

Phương pháp này đơn giản, dễ thực hiện và phù hợp với nhiều đối tượng.

Các bước thực hiện:

1. Bước 1: Xác định các điểm đặc biệt trên parabol (ví dụ: đỉnh). Lưu ý rằng các điểm này đối xứng nhau qua trục của parabol.
2. Bước 2: Vẽ hệ trục tọa độ Oxy.
3. Bước 3: Trên trục Ox, xác định tiêu điểm E và điểm M sao cho M là trung điểm của OE (OM = ME).
4. Bước 4: Chọn một điểm M’ bất kỳ trên đoạn ME. Kẻ đường thẳng đi qua M’ và song song với đường thẳng đã biết (đường chuẩn).
5. Bước 5: Dùng compa quay một vòng cung với bán kính bằng OM’. Giao điểm giữa cung này và đường thẳng song song với OM’ là một điểm thuộc parabol.
6. Bước 6: Lặp lại các bước 4 và 5 với các điểm M’ khác nhau trên đoạn ME. Nối các điểm vừa tìm được, ta sẽ có một đường parabol hoàn chỉnh.

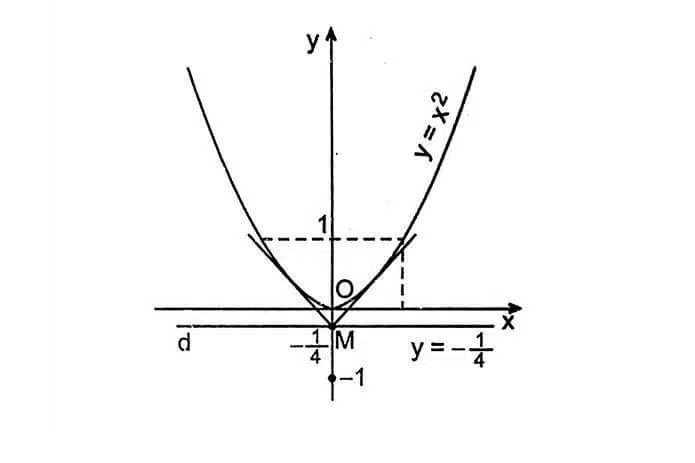
3.2. Vẽ Parabol Bằng Hàm Bậc Hai

Đồ thị của hàm số bậc hai y = ax² + bx + c (a ≠ 0) là một đường parabol.

Các bước thực hiện:

1. Bước 1: Xác định tọa độ đỉnh của parabol: (-b/2a; -Δ/4a), trong đó Δ = b² – 4ac.
2. Bước 2: Xác định trục đối xứng của parabol: x = -b/2a (đường thẳng đi qua đỉnh và song song với trục tung).
3. Bước 3: Xác định tọa độ giao điểm của parabol với trục tung (0; c) và trục hoành (nếu có). Tìm thêm một số điểm khác thuộc đồ thị (ví dụ: điểm đối xứng với (0; c) qua trục đối xứng).
4. Bước 4: Dựa vào tính chất đối xứng, bề lõm và hình dạng của parabol, nối các điểm lại để hoàn thành đồ thị.

Lưu ý:

• Khi vẽ parabol y = ax² + bx + c (a ≠ 0), cần chú ý đến dấu của hệ số a:
  • Nếu a > 0: Bề lõm của parabol hướng lên trên.
  • Nếu a < 0: Bề lõm của parabol hướng xuống dưới.
• Số lượng điểm xác định trên đồ thị càng nhiều, độ chính xác của parabol càng cao.

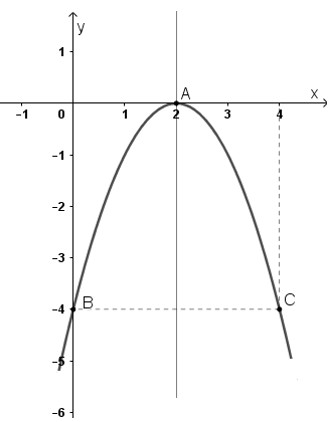
Ví dụ 1: Lập bảng biến thiên và vẽ đồ thị của hàm số y = -x² + 4x - 4.

Lời giải:

• Tập xác định: R.
• Đỉnh I(2; 0).
• Trục đối xứng: x = 2.
• Giao điểm với trục hoành: A(2; 0).
• Giao điểm với trục tung: B(0; -4).
• Điểm đối xứng với B qua x = 2: C(4; -4).

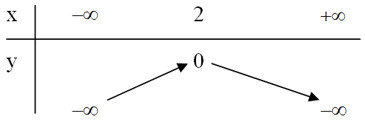
Bảng biến thiên:

Đồ thị hàm số:

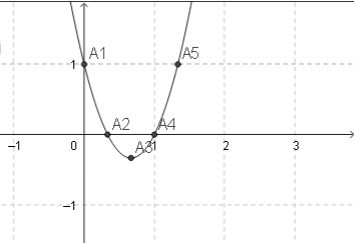
Ví dụ 2: Lập bảng biến thiên và vẽ đồ thị hàm số: y = 3x² - 4x + 1.

Lời giải:

• a = 3, b = -4, c = 1.
• Tập xác định: R.
• Tọa độ đỉnh: I(2/3; -1/3).
• Trục đối xứng: x = 2/3.
• Hàm số nghịch biến trên (-∞; 2/3) và đồng biến trên (2/3; +∞).
• Giao điểm với trục hoành: x = 1 và x = 1/3.
• Giao điểm với trục tung: y = 1.

Bảng biến thiên:

Đồ thị:

Đồ thị hàm số y = 3x² - 4x + 1 là một đường parabol (P) có đỉnh I(2/3; -1/3), trục đối xứng x = 2/3 và bề lõm quay lên trên.

4. Tương Quan Giữa Parabol và Đường Thẳng

4.1. Xác Định Tọa Độ Giao Điểm

Cho đường thẳng d: y = mx + n và parabol (P): y = ax² (a ≠ 0). Số giao điểm của d và (P) là số nghiệm của phương trình hoành độ giao điểm:

ax² = mx + n ⇔ ax² - mx - n = 0 (*)

• Nếu phương trình (*) có hai nghiệm phân biệt (Δ > 0), thì d cắt (P) tại hai điểm phân biệt.
• Nếu phương trình (*) có nghiệm kép (Δ = 0), thì d tiếp xúc với (P).
• Nếu phương trình (*) vô nghiệm (Δ < 0), thì d không cắt (P).

Phương pháp giải bài toán tìm tọa độ giao điểm:

1. Bước 1: Viết phương trình hoành độ giao điểm của parabol và đường thẳng.
2. Bước 2: Giải phương trình bậc hai, tìm hoành độ giao điểm.
3. Bước 3: Tìm tung độ giao điểm (nếu có).
4. Bước 4: Kết luận.

Các dạng bài thường gặp:

• Dạng 1: Xác định số giao điểm của đường thẳng và parabol.
• Dạng 2: Tìm tọa độ giao điểm của đường thẳng và parabol.
• Dạng 3: Xác định tham số m để đường thẳng và parabol cắt nhau tại điểm thỏa mãn điều kiện cho trước.
• Dạng 4: Bài toán liên quan đến diện tích tam giác, diện tích hình thang và chiều cao.

4.2. Ví Dụ Minh Họa

Ví dụ 1: Tìm tọa độ giao điểm của parabol y = x² và đường thẳng y = 2x - 1.

Lời giải:

Phương trình hoành độ giao điểm: x² = 2x - 1 ⇔ x² - 2x + 1 = 0 ⇔ (x - 1)² = 0 ⇔ x = 1.

Với x = 1, ta có y = 1² = 1.

Vậy tọa độ giao điểm của parabol y = x² và đường thẳng y = 2x - 1 là (1; 1).

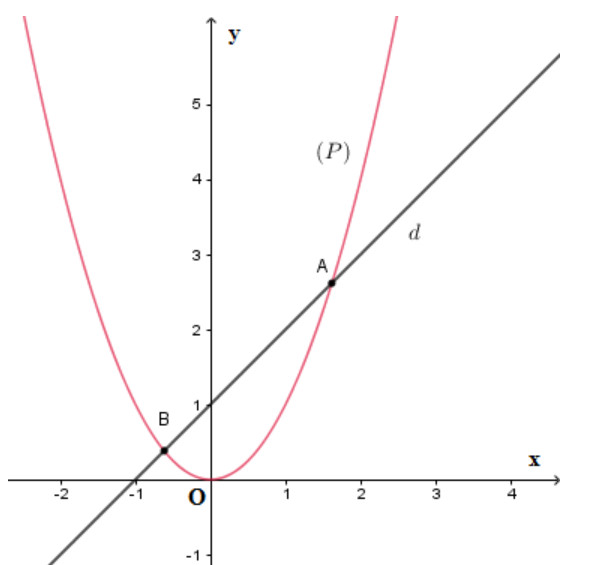
Ví dụ 2: Cho parabol (P): y = (1/2)x² và đường thẳng (d): y = x - m/2 (m là tham số). Tìm m để (d) tiếp xúc với (P) và tìm tọa độ tiếp điểm.

Lời giải:

Phương trình hoành độ giao điểm: (1/2)x² = x - m/2 ⇔ x² - 2x + m = 0 (*)

Δ' = b'² - ac = (-1)² - 1.m = 1 - m.

Đường thẳng (d) tiếp xúc với parabol (P) khi và chỉ khi phương trình (*) có nghiệm kép, tức là Δ' = 0 ⇔ m = 1.

Khi đó, nghiệm của phương trình (*) là x = -b'/a = -(-2)/(2.1) = 1.

Với x = 1, ta có y = (1/2).1² = 1/2.

Vậy tọa độ tiếp điểm của parabol (P): y = (1/2)x² và đường thẳng (d): y = x - 1/2 là (1; 1/2).

Bạn muốn tìm hiểu sâu hơn về sự tương quan giữa parabol và đường thẳng, các bài tập nâng cao và phương pháp giải nhanh? Hãy truy cập tic.edu.vn ngay hôm nay!

5. FAQ – Giải Đáp Thắc Mắc Về Phương Trình Parabol

1. Phương trình parabol có ứng dụng gì trong thực tế?
   • Phương trình parabol được ứng dụng rộng rãi trong xây dựng (cầu, mái vòm), quang học (gương phản xạ, đèn pha), viễn thông (anten parabol) và nhiều lĩnh vực khác.
2. Làm thế nào để xác định đỉnh của parabol?
   • Đối với phương trình tổng quát y = ax² + bx + c, tọa độ đỉnh là (-b/2a; (b²-4ac)/4a). Đối với phương trình chính tắc y² = 2px, đỉnh là gốc tọa độ (0; 0).
3. Phương trình chính tắc của parabol là gì?
   • Phương trình chính tắc của parabol có dạng y² = 2px, trong đó p là tham số tiêu.
4. Làm thế nào để vẽ parabol bằng compa và thước kẻ?
   • Bạn có thể tham khảo hướng dẫn chi tiết ở mục 3.1 của bài viết này.
5. Làm thế nào để xác định số giao điểm của đường thẳng và parabol?
   • Số giao điểm là số nghiệm của phương trình hoành độ giao điểm.
6. Nếu delta < 0 thì đường thẳng và parabol có giao điểm không?
   • Không, nếu delta < 0 thì phương trình hoành độ giao điểm vô nghiệm, tức là đường thẳng và parabol không có giao điểm.
7. Trục đối xứng của parabol là gì?
   • Trục đối xứng là đường thẳng đi qua đỉnh của parabol và song song với trục tung.
8. Làm thế nào để tìm phương trình đường thẳng tiếp xúc với parabol?
   • Đường thẳng tiếp xúc với parabol khi và chỉ khi phương trình hoành độ giao điểm có nghiệm kép (delta = 0).
9. Website tic.edu.vn có những tài liệu gì về phương trình parabol?
   • tic.edu.vn cung cấp đầy đủ các tài liệu về định nghĩa, phương trình, cách vẽ, ứng dụng và bài tập về phương trình parabol, giúp bạn nắm vững kiến thức và rèn luyện kỹ năng giải toán.
10. Tôi có thể liên hệ với tic.edu.vn để được tư vấn về phương trình parabol không?
    • Bạn có thể liên hệ với tic.edu.vn qua email tic.edu@gmail.com hoặc truy cập website tic.edu.vn để được hỗ trợ và giải đáp thắc mắc.

Kết Luận

Hy vọng bài viết này đã cung cấp cho bạn đầy đủ thông tin về phương trình parabol, từ định nghĩa, các dạng phương trình, cách vẽ đồ thị đến ứng dụng thực tế và các bài tập minh họa. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục kiến thức. Hãy truy cập website của chúng tôi ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và tham gia cộng đồng học tập sôi nổi!

Đừng bỏ lỡ cơ hội:

• Truy cập tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và đa dạng.
• Tham gia cộng đồng học tập trực tuyến để trao đổi kiến thức và kinh nghiệm với các bạn học sinh, sinh viên khác.
• Liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc website tic.edu.vn để được tư vấn và hỗ trợ.

tic.edu.vn – Nền tảng giáo dục trực tuyến hàng đầu Việt Nam, nơi kiến thức được chia sẻ và đam mê được lan tỏa!