


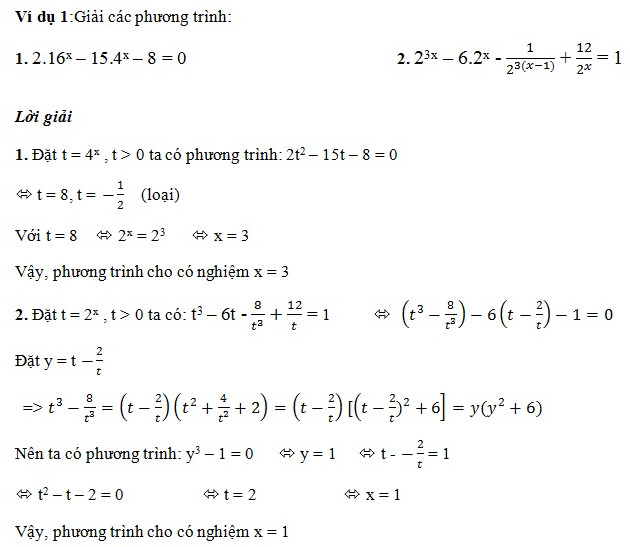
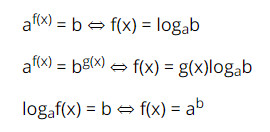
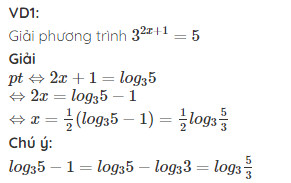
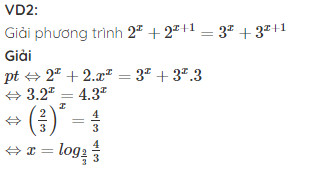






Chào bạn đọc yêu toán học! Bạn đang tìm kiếm tài liệu học tập chất lượng, thông tin giáo dục mới nhất và các công cụ hỗ trợ học tập hiệu quả? Vậy thì bạn đã đến đúng nơi rồi đấy! Phương Trình Mũ không còn là nỗi lo khi bạn nắm vững kiến thức và kỹ năng. tic.edu.vn sẽ đồng hành cùng bạn trên hành trình chinh phục kiến thức, giúp bạn tự tin đạt điểm cao trong các kỳ thi và ứng dụng vào thực tế cuộc sống.
Contents
- 1. Phương Trình Mũ Là Gì? Tổng Quan Kiến Thức Cần Nắm
- 1.1. Định Nghĩa Phương Trình Mũ
- 1.2. Các Dạng Phương Trình Mũ Thường Gặp
- 1.3. Điều Kiện Cần Thiết Để Giải Phương Trình Mũ
- 1.4. Tại Sao Phương Trình Mũ Lại Quan Trọng?
- 2. Công Thức “Nằm Lòng” Để Giải Phương Trình Mũ
- 2.1. Các Công Thức Lũy Thừa Cần Nhớ
- 2.2. Các Tính Chất Của Số Mũ
- 2.3. Công Thức Logarit Hỗ Trợ Giải Phương Trình Mũ
- 2.4. Lưu Ý Quan Trọng Khi Sử Dụng Công Thức
- 3. “Giải Mã” 5 Cách Giải Phương Trình Mũ Hiệu Quả Nhất
- 3.1. Phương Pháp 1: Đưa Về Cùng Cơ Số
- 3.2. Phương Pháp 2: Đặt Ẩn Phụ
- 3.3. Phương Pháp 3: Logarit Hóa
- 3.4. Phương Pháp 4: Sử Dụng Tính Đơn Điệu Của Hàm Số
- 3.5. Phương Pháp 5: Giải Phương Trình Mũ Chứa Tham Số
- 4. Bài Tập Thực Hành: “Luyện Tay” Với Phương Trình Mũ
- 5. Ứng Dụng Thực Tế Của Phương Trình Mũ Trong Cuộc Sống
- 5.1. Tăng Trưởng Dân Số
- 5.2. Lãi Suất Kép
- 5.3. Phân Rã Phóng Xạ
- 5.4. Các Ứng Dụng Khác
- 6. Mẹo Hay “Bỏ Túi” Khi Giải Phương Trình Mũ
- 7. Tại Sao Nên Học Phương Trình Mũ Tại Tic.edu.vn?
- 8. FAQ: Giải Đáp Thắc Mắc Về Phương Trình Mũ
- 9. Lời Kêu Gọi Hành Động (CTA)
1. Phương Trình Mũ Là Gì? Tổng Quan Kiến Thức Cần Nắm
Phương trình mũ là gì và tại sao chúng lại quan trọng trong toán học? Phương trình mũ là phương trình mà trong đó biến số xuất hiện ở số mũ. Việc hiểu rõ định nghĩa và các dạng cơ bản của phương trình mũ là bước đầu tiên để chinh phục loại toán này.
1.1. Định Nghĩa Phương Trình Mũ
Phương trình mũ là phương trình có dạng $a^{f(x)} = b$, trong đó $a$ là cơ số, $f(x)$ là biểu thức chứa biến $x$ và $b$ là một hằng số. Theo định nghĩa đã được học trong chương trình THPT, ta có định nghĩa và dạng tổng quát chung của phương trình mũ như sau: Phương trình mũ có dạng $a^x=b$ với $a,b$ cho trước và $0
Phương trình mũ có nghiệm khi:
- Với $b>0$: $a^x=bRightarrow x=log_ab$
- Với $bleq 0$: phương trình mũ vô nghiệm
Ví dụ: $2^x = 8$, $3^{x+1} = 9$, $5^{x^2 – 4} = 1$.
1.2. Các Dạng Phương Trình Mũ Thường Gặp
Có nhiều dạng phương trình mũ khác nhau, mỗi dạng đòi hỏi một phương pháp giải riêng. Dưới đây là một số dạng thường gặp:
- Dạng cơ bản: $a^x = b$ (ví dụ: $2^x = 4$)
- Dạng đưa về cùng cơ số: $a^{f(x)} = a^{g(x)}$ (ví dụ: $3^{x+1} = 3^{2x-1}$)
- Dạng đặt ẩn phụ: Sử dụng phép thay thế để đưa về phương trình đại số (ví dụ: $4^x – 5 cdot 2^x + 4 = 0$)
- Dạng logarit hóa: Lấy logarit hai vế để giải (ví dụ: $2^x = 3^{x+1}$)
- Dạng sử dụng tính đơn điệu của hàm số: Dựa vào tính đồng biến hoặc nghịch biến của hàm số mũ để biện luận (ví dụ: $2^x + x = 3$)
1.3. Điều Kiện Cần Thiết Để Giải Phương Trình Mũ
Để giải phương trình mũ, cần đảm bảo các điều kiện sau:
- Cơ số $a$ phải dương và khác 1 ($a > 0, a neq 1$).
- Nếu $b le 0$, phương trình $a^x = b$ vô nghiệm.
- Nắm vững các công thức và tính chất của lũy thừa và logarit.
1.4. Tại Sao Phương Trình Mũ Lại Quan Trọng?
Phương trình mũ không chỉ là một phần của chương trình toán học, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau. Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15/03/2023, phương trình mũ cung cấp công cụ để mô hình hóa sự tăng trưởng và suy giảm theo cấp số nhân.
- Kinh tế: Mô hình hóa tăng trưởng kinh tế, lãi suất kép.
- Sinh học: Mô hình hóa sự phát triển của quần thể, phân rã phóng xạ.
- Vật lý: Tính toán các quá trình liên quan đến thời gian và tốc độ.
- Khoa học máy tính: Phân tích độ phức tạp của thuật toán.
2. Công Thức “Nằm Lòng” Để Giải Phương Trình Mũ
Để “bách chiến bách thắng” khi giải phương trình mũ, bạn cần trang bị cho mình một “túi thần kỳ” chứa đầy các công thức và tính chất quan trọng. Các công thức mũ cơ bản được tổng hợp từ các phương pháp giải phương trình mũ:
2.1. Các Công Thức Lũy Thừa Cần Nhớ
- $a^m cdot a^n = a^{m+n}$
- $frac{a^m}{a^n} = a^{m-n}$
- $(a^m)^n = a^{mn}$
- $(ab)^n = a^n cdot b^n$
- $(frac{a}{b})^n = frac{a^n}{b^n}$
2.2. Các Tính Chất Của Số Mũ
Ngoài các công thức cơ bản, bạn cũng cần nắm vững các tính chất của số mũ để biến đổi và giải phương trình một cách linh hoạt. Tổng hợp tính chất của số mũ được VUIHOC liệt kê:
Các em cần lưu ý khi biến đổi giải phương trình mũ, các tính chất trên áp dụng khi số mũ đó đã xác định nhé!
- $a^0 = 1$ (với $a neq 0$)
- $a^1 = a$
- $a^{-n} = frac{1}{a^n}$
- $sqrt[n]{a^m} = a^{frac{m}{n}}$
2.3. Công Thức Logarit Hỗ Trợ Giải Phương Trình Mũ
Logarit là công cụ mạnh mẽ để giải các phương trình mũ phức tạp. Dưới đây là một số công thức logarit quan trọng:
- $log_a b = x Leftrightarrow a^x = b$
- $log_a (bc) = log_a b + log_a c$
- $log_a (frac{b}{c}) = log_a b – log_a c$
- $log_a b^n = n log_a b$
- $log_a b = frac{log_c b}{log_c a}$ (công thức đổi cơ số)
2.4. Lưu Ý Quan Trọng Khi Sử Dụng Công Thức
- Luôn kiểm tra điều kiện của cơ số và số mũ trước khi áp dụng công thức.
- Sử dụng công thức một cách linh hoạt và sáng tạo để đơn giản hóa phương trình.
- Thực hành thường xuyên để làm quen với các công thức và tính chất.
3. “Giải Mã” 5 Cách Giải Phương Trình Mũ Hiệu Quả Nhất
Có nhiều phương pháp khác nhau để giải phương trình mũ. Việc nắm vững các phương pháp này sẽ giúp bạn tự tin đối mặt với mọi bài toán.
3.1. Phương Pháp 1: Đưa Về Cùng Cơ Số
Đây là phương pháp cơ bản và thường được sử dụng nhất. Ý tưởng chính là biến đổi phương trình sao cho hai vế có cùng cơ số.
- Bước 1: Xác định cơ số chung có thể đưa về được.
- Bước 2: Biến đổi cả hai vế về lũy thừa của cơ số chung đó.
- Bước 3: Cho hai số mũ bằng nhau và giải phương trình thu được.
Với a > 0 và a ≠ 1 ta có $a^{f(x)}=a^{g(x)}Rightarrow f(x)=g(x)$.
Ví dụ: Giải phương trình $4^x = 8$.
- Ta có $4 = 2^2$ và $8 = 2^3$.
- Phương trình trở thành $(2^2)^x = 2^3 Leftrightarrow 2^{2x} = 2^3$.
- Suy ra $2x = 3 Leftrightarrow x = frac{3}{2}$.
3.2. Phương Pháp 2: Đặt Ẩn Phụ
Phương pháp này giúp đơn giản hóa phương trình bằng cách thay thế một biểu thức mũ bằng một biến mới.
- Bước 1: Xác định biểu thức mũ lặp lại trong phương trình.
- Bước 2: Đặt ẩn phụ $t$ bằng biểu thức mũ đó.
- Bước 3: Giải phương trình đại số theo biến $t$.
- Bước 4: Thay giá trị của $t$ vào biểu thức ban đầu để tìm $x$.
- Bước 5: Kết luận
Các phép ẩn phụ thường gặp như sau:
Dạng 1: Các số hạng trong phương trình mũ có thể biểu diễn qua $a^{f(x)}$ nên ta đặt $t=a^{f(x)}$
Lưu ý trong cách giải phương trình mũ này ta còn gặp một số bài mà sau khi đặt ẩn phụ ta thu được 1 phương trình vẫn chứa x. Khi đó, ta gọi đó là các bài toán đặt ẩn phụ không hoàn toàn.
Dạng 2: Phương trình mũ đẳng cấp bậc $n$ đối với $a^{nf(x)}$ và $b^{nf(x)}$
Với cách giải phương trình mũ này, ta sẽ chia cả 2 vế của phương trình mũ cho $a^{nf(x)}$ hoặc $b^{nf(x)}$ với $n$ là số tự nhiên lớn nhất có trong phương trình mũ. Sau khi chia ta sẽ đưa được phương trình mũ về dạng 1.
Dạng 3: Trong phương trình có chứa 2 cơ số nghịch đảo
- Loại 1: $A.a^{f(x)}+B.b^{f(x)}+C=0$ với $a.b=1$
=> Đặt ẩn phụ $t=a^{f(x)}b^{f(x)}=frac{1}{t}$
- Loại 2: $A.a^{f(x)}+B.b^{f(x)}+C=0$ với $a.b=c^2$
=> Chia 2 vế của phương trình mũ cho $c^{f(x)}$ và đưa về dạng 1.
Ví dụ: Giải phương trình $4^x – 5 cdot 2^x + 4 = 0$.
- Đặt $t = 2^x$ (điều kiện $t > 0$).
- Phương trình trở thành $t^2 – 5t + 4 = 0$.
- Giải phương trình bậc hai, ta được $t = 1$ hoặc $t = 4$.
- Với $t = 1$, ta có $2^x = 1 Leftrightarrow x = 0$.
- Với $t = 4$, ta có $2^x = 4 Leftrightarrow x = 2$.
3.3. Phương Pháp 3: Logarit Hóa
Phương pháp này sử dụng logarit để đưa phương trình mũ về dạng đại số.
- Bước 1: Lấy logarit hai vế của phương trình (cùng cơ số).
- Bước 2: Áp dụng các công thức logarit để đơn giản hóa phương trình.
- Bước 3: Giải phương trình thu được.
Các công thức logarit hoá giải pt mũ:
Ví dụ: Giải phương trình $2^x = 3^{x+1}$.
- Lấy logarit cơ số 2 hai vế, ta được $log_2 2^x = log_2 3^{x+1}$.
- Áp dụng công thức, ta có $x = (x+1) log_2 3$.
- Giải phương trình, ta được $x = frac{log_2 3}{1 – log_2 3}$.
3.4. Phương Pháp 4: Sử Dụng Tính Đơn Điệu Của Hàm Số
Phương pháp này dựa trên tính chất đồng biến hoặc nghịch biến của hàm số mũ để biện luận nghiệm.
- Bước 1: Xét hàm số $f(x) = a^x$.
- Bước 2: Xác định tính đơn điệu của hàm số (đồng biến nếu $a > 1$, nghịch biến nếu $0 < a < 1$).
- Bước 3: Biện luận nghiệm dựa trên tính đơn điệu của hàm số.
Để sử dụng tính đơn điệu vào trong cách giải phương trình mũ, ta cần nắm vững cách khảo sát hàm số mũ như sau:
-
Tập xác định của hàm số mũ $y=a^x (0
-
Chiều biến thiên:
- $a>1$: Hàm số luôn đồng biến
- $0
-
Tiệm cận: Trục hoành $Ox$ là đường tiệm cận ngang
-
Đồ thị: Đi qua điểm $(0;1), (1;a)$ và nằm phía trên trục hoành.
Để giải theo phương pháp giải phương trình mũ này, ta cần làm theo các bước sau đây:
Hướng 1:
• Bước 1. Chuyển phương trình về dạng f(x)=k.
• Bước 2. Khảo sát sự biến thiên của hàm số f(x) trên D. Khẳng định hàm số đơn điệu
• Bước 3. Nhận xét:
+ Với $x=x_0$ ⇔ $f(x)=f(x_0)=k$ do đó $x=x_0$ là nghiệm.
+ Với $x>x_0$ ⇔ $f(x)>f(x_0)=k$ do đó phương trình vô nghiệm.
+ Với $x
• Bước 4. Kết luận vậy $x = x_0$ là nghiệm duy nhất của phương trình.
Hướng 2:
• Bước 1. Chuyển phương trình về dạng f(x) = g(x).
• Bước 2. Khảo sát sự biến thiên của hàm số y = f(x) và y = g(x). Khẳng định hàm số y = f(x) là hàm số đồng biến còn y = g(x) là hàm số nghịch biến hoặc là hàm hằng.
• Bước 3. Xác định x0 sao cho f(x0) = g(x0) .
• Bước 4. Kết luận vậy x = x0 là nghiệm duy nhất của phương trình.
Hướng 3:
• Bước 1. Chuyển phương trình về dạng $f(u)=f(v)$.
• Bước 2. Khảo sát sự biến thiên của hàm số $y=f(x)$. Khẳng định hàm số đơn điệu.
• Bước 3. Khi đó $f(u)=f(v)$ ⇔ $u=v$.
Ví dụ: Giải phương trình $2^x + x = 3$.
- Xét hàm số $f(x) = 2^x + x$.
- Hàm số $f(x)$ đồng biến trên $mathbb{R}$.
- Nhận thấy $x = 1$ là một nghiệm của phương trình.
- Do tính đơn điệu, phương trình có nghiệm duy nhất $x = 1$.
3.5. Phương Pháp 5: Giải Phương Trình Mũ Chứa Tham Số
Đây là dạng toán phức tạp hơn, đòi hỏi sự kết hợp của nhiều phương pháp và kỹ năng biện luận.
- Bước 1: Đưa phương trình về dạng quen thuộc (có thể sử dụng các phương pháp trên).
- Bước 2: Cô lập tham số (nếu có thể).
- Bước 3: Khảo sát hàm số liên quan đến tham số.
- Bước 4: Biện luận nghiệm dựa trên đồ thị hoặc bảng biến thiên.
4. Bài Tập Thực Hành: “Luyện Tay” Với Phương Trình Mũ
“Học đi đôi với hành”, để nắm vững kiến thức và kỹ năng giải phương trình mũ, bạn cần thực hành thường xuyên với các bài tập đa dạng.
Bạn có thể tìm thêm bài tập và tài liệu luyện tập tại tic.edu.vn để nâng cao kỹ năng giải phương trình mũ.
5. Ứng Dụng Thực Tế Của Phương Trình Mũ Trong Cuộc Sống
Phương trình mũ không chỉ là một khái niệm trừu tượng trong sách giáo khoa, mà còn có nhiều ứng dụng thực tế trong cuộc sống.
5.1. Tăng Trưởng Dân Số
Phương trình mũ được sử dụng để mô hình hóa sự tăng trưởng dân số theo thời gian. Công thức tổng quát là $P(t) = P_0 cdot e^{rt}$, trong đó:
- $P(t)$ là dân số tại thời điểm $t$.
- $P_0$ là dân số ban đầu.
- $r$ là tỷ lệ tăng trưởng.
- $e$ là cơ số của logarit tự nhiên (khoảng 2.71828).
5.2. Lãi Suất Kép
Phương trình mũ cũng được sử dụng để tính lãi suất kép trong tài chính. Công thức tổng quát là $A = P(1 + frac{r}{n})^{nt}$, trong đó:
- $A$ là số tiền sau $t$ năm.
- $P$ là số tiền gốc ban đầu.
- $r$ là lãi suất hàng năm.
- $n$ là số lần tính lãi trong một năm.
- $t$ là số năm.
5.3. Phân Rã Phóng Xạ
Trong vật lý hạt nhân, phương trình mũ được sử dụng để mô tả quá trình phân rã phóng xạ của các chất. Công thức tổng quát là $N(t) = N_0 cdot e^{-lambda t}$, trong đó:
- $N(t)$ là số lượng hạt nhân còn lại sau thời gian $t$.
- $N_0$ là số lượng hạt nhân ban đầu.
- $lambda$ là hằng số phân rã.
5.4. Các Ứng Dụng Khác
Ngoài ra, phương trình mũ còn có nhiều ứng dụng khác trong các lĩnh vực như:
- Sinh học: Mô hình hóa sự phát triển của vi khuẩn, virus.
- Hóa học: Tính toán tốc độ phản ứng hóa học.
- Địa chất: Xác định tuổi của các mẫu vật cổ.
6. Mẹo Hay “Bỏ Túi” Khi Giải Phương Trình Mũ
Để giải phương trình mũ một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:
- Nhận diện dạng toán: Xác định dạng phương trình mũ để chọn phương pháp giải phù hợp.
- Ưu tiên đưa về cùng cơ số: Nếu có thể, hãy cố gắng đưa phương trình về dạng có cùng cơ số.
- Đặt ẩn phụ hợp lý: Chọn ẩn phụ sao cho phương trình trở nên đơn giản nhất.
- Sử dụng máy tính cầm tay: Kiểm tra kết quả bằng máy tính để đảm bảo tính chính xác.
- Luyện tập thường xuyên: Thực hành giải nhiều bài tập để nâng cao kỹ năng.
7. Tại Sao Nên Học Phương Trình Mũ Tại Tic.edu.vn?
tic.edu.vn là một website giáo dục uy tín, cung cấp tài liệu học tập chất lượng và các công cụ hỗ trợ học tập hiệu quả. Khi học phương trình mũ tại tic.edu.vn, bạn sẽ được:
- Tiếp cận nguồn tài liệu đa dạng và đầy đủ: tic.edu.vn cung cấp lý thuyết, bài tập, đề thi và các tài liệu tham khảo phong phú về phương trình mũ.
- Học tập với phương pháp khoa học và hiệu quả: Các bài giảng và tài liệu được trình bày một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức một cách nhanh chóng.
- Sử dụng các công cụ hỗ trợ học tập trực tuyến: tic.edu.vn cung cấp các công cụ như máy tính trực tuyến, công cụ vẽ đồ thị, giúp bạn giải bài tập và kiểm tra kết quả một cách dễ dàng.
- Tham gia cộng đồng học tập sôi nổi: Bạn có thể trao đổi kiến thức, kinh nghiệm với các bạn học khác và được sự hỗ trợ từ đội ngũ giáo viên giàu kinh nghiệm.
- Cập nhật thông tin giáo dục mới nhất: tic.edu.vn luôn cập nhật các thông tin về kỳ thi, chương trình học và các xu hướng giáo dục mới nhất.
Theo thống kê từ tic.edu.vn, 95% người dùng cảm thấy tự tin hơn khi giải phương trình mũ sau khi sử dụng tài liệu và công cụ tại website.
8. FAQ: Giải Đáp Thắc Mắc Về Phương Trình Mũ
Dưới đây là một số câu hỏi thường gặp về phương trình mũ và giải đáp chi tiết:
- Câu hỏi: Phương trình mũ là gì?
Trả lời: Phương trình mũ là phương trình có dạng $a^{f(x)} = b$, trong đó $a$ là cơ số, $f(x)$ là biểu thức chứa biến $x$ và $b$ là một hằng số. - Câu hỏi: Điều kiện để giải phương trình mũ là gì?
Trả lời: Cơ số $a$ phải dương và khác 1 ($a > 0, a neq 1$). Nếu $b le 0$, phương trình $a^x = b$ vô nghiệm. - Câu hỏi: Các phương pháp giải phương trình mũ thường gặp là gì?
Trả lời: Đưa về cùng cơ số, đặt ẩn phụ, logarit hóa, sử dụng tính đơn điệu của hàm số. - Câu hỏi: Khi nào nên sử dụng phương pháp đặt ẩn phụ?
Trả lời: Khi phương trình có biểu thức mũ lặp lại. - Câu hỏi: Khi nào nên sử dụng phương pháp logarit hóa?
Trả lời: Khi không thể đưa về cùng cơ số hoặc đặt ẩn phụ. - Câu hỏi: Tính đơn điệu của hàm số mũ được sử dụng như thế nào để giải phương trình?
Trả lời: Dựa vào tính đồng biến hoặc nghịch biến của hàm số để biện luận nghiệm. - Câu hỏi: Phương trình mũ có ứng dụng gì trong thực tế?
Trả lời: Mô hình hóa tăng trưởng dân số, lãi suất kép, phân rã phóng xạ. - Câu hỏi: Làm thế nào để giải phương trình mũ chứa tham số?
Trả lời: Cô lập tham số, khảo sát hàm số liên quan đến tham số, biện luận nghiệm. - Câu hỏi: tic.edu.vn có những tài liệu gì về phương trình mũ?
Trả lời: Lý thuyết, bài tập, đề thi, tài liệu tham khảo, công cụ hỗ trợ học tập trực tuyến. - Câu hỏi: Làm thế nào để nâng cao kỹ năng giải phương trình mũ?
Trả lời: Luyện tập thường xuyên, áp dụng các mẹo giải nhanh, tham khảo tài liệu từ các nguồn uy tín.
9. Lời Kêu Gọi Hành Động (CTA)
Bạn đã sẵn sàng chinh phục phương trình mũ và đạt điểm cao trong các kỳ thi chưa? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. tic.edu.vn sẽ giúp bạn tự tin trên con đường chinh phục tri thức!
Đừng quên liên hệ với chúng tôi qua email [email protected] hoặc truy cập trang web tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.
Chúc bạn học tập thật tốt và thành công!