**Phương Trình Hypebol: Định Nghĩa, Ứng Dụng và Bài Tập Mới Nhất**

Phương Trình Hypebol là một khái niệm quan trọng trong hình học giải tích, mở ra cánh cửa khám phá những đường cong độc đáo và ứng dụng rộng rãi. Tại tic.edu.vn, chúng tôi cung cấp một cái nhìn toàn diện về phương trình hypebol, từ định nghĩa cơ bản đến các bài tập nâng cao, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài toán.

1. Hypebol Là Gì? Định Nghĩa Chi Tiết Nhất

Hypebol, hay còn gọi là đường hypebol, là một dạng đường conic đặc biệt. Nó được hình thành khi một mặt phẳng cắt một mặt nón đôi sao cho mặt phẳng đó cắt cả hai phần của nón.

Hiểu một cách chính xác hơn, đường hypebol là tập hợp tất cả các điểm trên mặt phẳng sao cho giá trị tuyệt đối của hiệu khoảng cách từ mỗi điểm đến hai điểm cố định (gọi là tiêu điểm) là một hằng số không đổi. Hằng số này thường được ký hiệu là 2a, trong đó a là độ dài bán trục thực của hypebol.

Hai điểm cố định F1 và F2 được gọi là tiêu điểm của hypebol. Đường thẳng đi qua hai tiêu điểm này là trục thực của hypebol, và trung điểm của đoạn thẳng nối hai tiêu điểm là tâm của hypebol.

Định nghĩa bằng ký hiệu:

Cho hai điểm cố định F1, F2 sao cho F1F2 = 2c (c > 0) và một hằng số a (0 < a < c).

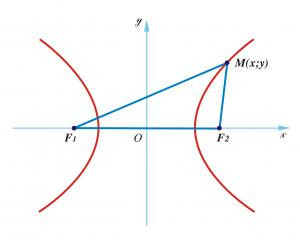
Đường hypebol (H) là tập hợp các điểm M thỏa mãn điều kiện: |MF1 – MF2| = 2a

Trong đó:

• F1 và F2 là các tiêu điểm của hypebol (H)
• Khoảng cách F1F2 = 2c là tiêu cự của hypebol (H)

2. Phương Trình Chính Tắc Của Đường Hypebol: Bí Mật Nằm Ở Đâu?

2.1. Thiết Lập Phương Trình Đường Cong Hypebol

Trong hệ tọa độ Oxy, giả sử hai tiêu điểm của hypebol là F1(-c; 0) và F2(c; 0).

Khi đó, một điểm M(x; y) thuộc hypebol (H) khi và chỉ khi:

x²/a² – y²/b² = 1

Với b² = c² – a²

Phương trình trên được gọi là phương trình chính tắc của hypebol.

2.2. Ví Dụ Minh Họa

Ví dụ 1: Xác định phương trình chính tắc của hypebol (H), biết rằng trục thực và trục ảo của (H) lần lượt là 10 và 6.

Hướng dẫn giải:

• Độ dài trục thực là 2a = 10 => a = 5
• Độ dài trục ảo là 2b = 6 => b = 3

Vậy phương trình chính tắc của hypebol (H) là: x²/5² – y²/3² = 1

Ví dụ 2: Viết phương trình chính tắc của hypebol, biết một đỉnh của hypebol là A2(5; 0) và một đường tiệm cận của hypebol là y = -3x.

Hướng dẫn giải:

Giả sử phương trình chính tắc của hypebol có dạng: x²/a² – y²/b² = 1 (với a > 0, b > 0)

• Hypebol có đỉnh A2(5; 0) => a = 5
• Hypebol có đường tiệm cận y = -3x => b/a = 3 => b = 3a = 15

Vậy phương trình chính tắc của hypebol là: x²/5² – y²/15² = 1 hay x²/25 – y²/225 = 1

3. Hình Dạng và Tính Chất Của Đường Hypebol: Khám Phá Những Điều Thú Vị

Đường hypebol sở hữu những đặc điểm và tính chất độc đáo sau:

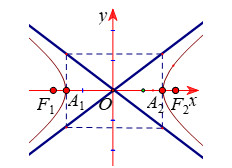
• Tiêu điểm: Hypebol có hai tiêu điểm, ký hiệu là F1(-c; 0) và F2(c; 0).

• Đỉnh: Hypebol có hai đỉnh, ký hiệu là A1(-a; 0) và A2(a; 0).

• Trục: Trục Ox là trục thực và trục Oy là trục ảo. Độ dài đoạn thẳng nối hai đỉnh (2a) được gọi là độ dài trục thực, và độ dài đoạn thẳng vuông góc với trục thực, đi qua tâm và có độ dài 2b được gọi là độ dài trục ảo.

• Nhánh: Đường hypebol gồm hai nhánh nằm về hai phía của trục ảo.

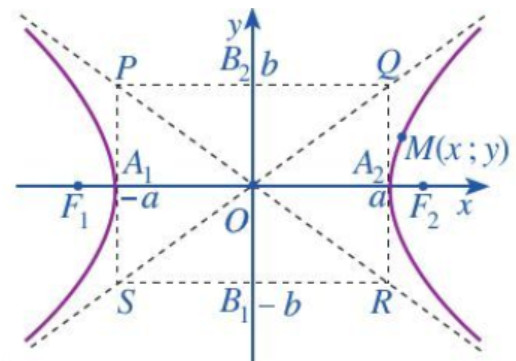
• Hình chữ nhật cơ sở: Hình chữ nhật được tạo bởi các đường thẳng x = ±a và y = ±b được gọi là hình chữ nhật cơ sở của hypebol.

• Đường tiệm cận: Hai đường thẳng chứa hai đường chéo của hình chữ nhật cơ sở là hai đường tiệm cận của hypebol. Phương trình của hai đường tiệm cận là y = ±(b/a)x.

• Tâm sai: Tâm sai của hypebol được ký hiệu là e và được tính bằng công thức e = c/a, trong đó e > 1.

• Khoảng cách từ điểm M(xM; yM) trên hypebol đến hai tiêu điểm:

  • MF1 = |a + exM| = |a + (c/a)xM|
  • MF2 = |a – exM| = |a – (c/a)xM|

Ví dụ 1: Xác định tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực, độ dài trục ảo và phương trình các đường tiệm cận của các hypebol sau:

a) x²/9 – y²/4 = 1

b) x²/9 – y²/16 = 1

c) x² – 9y² = 9

Hướng dẫn giải:

a) Ta có: a = 3, b = 2, c = √(a² + b²) = √13

*   Tiêu điểm: F1(-√13; 0), F2(√13; 0)
*   Đỉnh: A1(-3; 0), A2(3; 0)
*   Độ dài trục thực: 2a = 6
*   Độ dài trục ảo: 2b = 4
*   Phương trình tiệm cận: y = ±(2/3)x

b) Ta có: a = 3, b = 4, c = √(a² + b²) = 5

*   Tiêu điểm: F1(-5; 0), F2(5; 0)
*   Đỉnh: A1(-3; 0), A2(3; 0)
*   Độ dài trục thực: 2a = 6
*   Độ dài trục ảo: 2b = 8
*   Phương trình tiệm cận: y = ±(4/3)x

c) Ta có: x² – 9y² = 9 <=> x²/9 – y²/1 = 1

*   a = 3, b = 1, c = √(a² + b²) = √10
*   Tiêu điểm: F1(-√10; 0), F2(√10; 0)
*   Đỉnh: A1(-3; 0), A2(3; 0)
*   Độ dài trục thực: 2a = 6
*   Độ dài trục ảo: 2b = 2
*   Phương trình tiệm cận: y = ±(1/3)x

Ví dụ 2: Cho hypebol (H) như hình vẽ:

a) Chứng minh rằng nếu M(x; y) nằm trên hypebol (H) thì x ≤ -a hoặc x ≥ a.

b) Xác định phương trình của hai đường thẳng PR và QS.

Hướng dẫn giải:

a) Nếu M(x; y) thuộc hypebol (H) thì x²/a² – y²/b² = 1

Mà y²/b² ≥ 0 => x²/a² ≥ 1

Do đó x² ≥ a² => x ≤ -a hoặc x ≥ a

b) Ta có P(-a; b), R(a; -b) => vectơ PR = (2a; -2b)

Chọn vectơ pháp tuyến của PR là n(b; a)

Phương trình đường thẳng PR có dạng: b(x + a) + a(y - b) = 0

Hay bx + ay = 0 <=> y = -(b/a)x

Tương tự, ta có Q(a; b), S(-a; -b) => vectơ QS = (-2a; -2b)

Chọn vectơ pháp tuyến của QS là n(b; a)

Phương trình đường thẳng QS có dạng: -b(x - a) + a(y - b) = 0

Hay -bx + ay = 0 <=> y = (b/a)x

4. Bài Tập Vận Dụng Về Đường Hypebol: Thử Sức Ngay!

Câu 1: Định nghĩa nào sau đây mô tả đúng về đường hypebol?

A. Tập hợp các điểm cách đều một điểm cố định và một đường thẳng cố định.

B. Tập hợp các điểm sao cho tổng khoảng cách đến hai điểm cố định là một hằng số.

C. Tập hợp các điểm sao cho hiệu khoảng cách đến hai điểm cố định có giá trị tuyệt đối là một hằng số.

D. Tập hợp các điểm cách đều một đường tròn cố định.

Câu 2: Cho hypebol (H) có phương trình chính tắc x²/a² – y²/b² = 1 (a, b > 0). Mệnh đề nào sau đây đúng?

A. Tiêu điểm của (H) là F1(c; 0) và F2(-c; 0) với c² = a² – b².

B. Tiêu điểm của (H) là F1(0; c) và F2(0; -c) với c² = a² + b².

C. Tiêu điểm của (H) là F1(c; 0) và F2(-c; 0) với c² = a² + b².

D. Tiêu điểm của (H) là F1(0; c) và F2(0; -c) với c² = a² – b².

Câu 3: Cho hypebol (H) có phương trình chính tắc x²/a² – y²/b² = 1 (a, b > 0). Phát biểu nào sau đây đúng?

A. Tâm sai của hypebol là e = c/b với c² = a² + b².

B. Tâm sai của hypebol là e = a/c với c² = a² + b².

C. Tâm sai của hypebol là e = c/a với c² = a² – b².

D. Tâm sai của hypebol là e = c/a với c² = a² + b².

Câu 4: Cho đường hypebol (H) có phương trình chính tắc x²/a² – y²/b² = 1 (a, b > 0). Khẳng định nào sau đây là sai?

A. Các đỉnh của (H) nằm trên trục thực có tọa độ (a; 0) và (-a; 0).

B. Các đỉnh của (H) nằm trên trục ảo có tọa độ (0; b) và (0; -b).

C. Độ dài tiêu cự của (H) là 2c với c² = a² + b².

D. Tâm sai của (H) là e = c/a với c² = a² + b².

Câu 5: Hypebol x²/16 – y²/9 = 1 có hai tiêu điểm là:

A. F1(-5; 0) và F2(5; 0)

B. F1(-√7; 0) và F2(√7; 0)

C. F1(-3; 0) và F2(3; 0)

D. F1(-4; 0) và F2(4; 0)

Câu 6: Đường hypebol có nửa trục thực bằng 4, tiêu cự bằng 10 có phương trình chính tắc là:

A. x²/16 – y²/9 = 1

B. x²/16 + y²/9 = 1

C. y²/16 – x²/9 = 1

D. x²/16 – y²/25 = 1

Câu 7: Tìm phương trình chính tắc của đường hypebol (H) biết rằng hình chữ nhật cơ sở của (H) có một đỉnh là (2; -3).

A. x²/2 – y²/-3 = 1

B. x²/4 – y²/9 = 1

C. x²/9 – y²/3 = 1

D. x²/2 – y²/3 = 1

Câu 8: Đường hypebol x²/4 – y²/9 = 1 có:

A. Hai đỉnh A1(-2; 0), A2(2; 0) và tâm sai e = 2/√13

B. Hai đường tiệm cận y = ±(3/2)x và tâm sai e = 2/√13

C. Hai đường tiệm cận y = ±(3/2)x và tâm sai e = √13/2

D. Hai tiêu điểm F1(-2; 0), F2(2; 0) và tâm sai e = 2/√13

Câu 9: Phương trình hai đường tiệm cận y = ±(3/2)x là của đường hypebol nào sau đây?

A. x²/4 – y²/9 = 1

B. x²/3 – y²/2 = 1

C. x²/2 – y²/3 = 1

D. x²/9 – y²/4 = 1

Câu 10: Tìm phương trình chính tắc của hypebol (H) biết (H) đi qua điểm (√5; 4) và một đường tiệm cận có phương trình là x + y = 0.

A. x² – y²/9 = 1

B. x² – y² = 9

C. x² – y² = 1

D. x²/5 – y²/4 = 1

Câu 11: Tìm phương trình chính tắc của đường hypebol (H) biết (H) có tiêu điểm là (3; 0) và một đường tiệm cận có phương trình là √2x + y = 0.

A. x²/1 – y²/8 = 1

B. x²/3 – y²/6 = 1

C. x²/1 – y²/2 = 1

D. x²/6 – y²/3 = 1

Câu 12: Tìm phương trình chính tắc của đường hypebol (H) biết một đỉnh của hình chữ nhật cơ sở của (H) là M(4; 3).

A. x²/16 – y²/9 = 1

B. x²/4 – y²/3 = 1

C. x²/16 – y²/4 = 1

D. x²/4 – y²/9 = 1

Câu 13: Cho điểm M nằm trên đường hypebol (H): x²/16 – y²/9 = 1. Nếu hoành độ của điểm M bằng 8 thì khoảng cách từ M đến các tiêu điểm của H là bao nhiêu?

A. 8 ± 4√2

B. 8 ± 4√5

C. 5 và 13

D. 1 và 15

Câu 14: Viết phương trình chính tắc của đường hypebol, biết giá trị tuyệt đối của hiệu các bán kính qua tiêu điểm của điểm M bất kỳ trên hypebol là 8, tiêu cự bằng 10.

A. x²/16 – y²/9 = 1

B. x²/16 – y²/9 = 1 hoặc -x²/16 + y²/9 = 1

C. x²/4 + y²/3 = 1

D. x²/4 – y²/3 = 1

Câu 15: Đường hypebol có hai đường tiệm cận vuông góc với nhau, độ dài trục thực bằng 6, có phương trình chính tắc là:

A. x²/36 – y²/6 = 1

B. x²/9 – y²/9 = 1

C. x²/1 – y²/9 = 1

D. x²/16 – y²/9 = 1

Câu 16: Điểm nào trong các điểm M(5; 0), N(10; 3√3), P(5√2; 3√2), Q(5; 4) nằm trên một đường tiệm cận của đường hypebol x²/25 – y²/9 = 1?

A. N

B. M

C. Q

D. P

Câu 17: Tìm phương trình chính tắc của đường hypebol (H) biết (H) có một đường tiệm cận là x – 2y = 0 và hình chữ nhật cơ sở của nó có diện tích bằng 24.

A. x²/12 – y²/48 = 1

B. x²/3 – y²/12 = 1

C. x²/12 – y²/3 = 1

D. x²/48 – y²/12 = 1

Câu 18: Lập phương trình chính tắc của đường hypebol (H) với trục Ox là trục thực, tổng hai bán trục a + b = 7, phương trình hai tiệm cận là y = ±(3/4)x.

A. (H): x²/3 – y²/4 = 1

B. (H): x²/4 – y²/3 = 1

C. (H): x²/16 – y²/9 = 1

D. (H): x²/9 – y²/16 = 1

Câu 19: Cho đường hypebol (H): x²/25 – y²/16 = 1 có hai tiêu điểm F1, F2. Với M là một điểm tùy ý thuộc (H). Tính S = (MF1 + MF2)² – 4OM².

A. 8

B. 1

C. 1/64

D. 64

Câu 20: Cho đường hypebol (H): x²/4 – y²/3 = 1. Lập phương trình tiếp tuyến của (H) song song với đường thẳng d: 5x – 4y + 10 = 0.

A. 5x – 4y + 4 = 0, 5x – 5y – 4 = 0

B. 5x – 4y – 16 = 0 và 5x – 4y + 16 = 0

C. 5x – 4y – 16 = 0

D. 5x – 4y + 16 = 0

Đáp án:

1	2	3	4	5	6	7	8	9	10
C	C	D	B	A	A	B	C	A	C
11	12	13	14	15	16	17	18	19	20
D	A	D	A	B	D	C	C	D	B

5. Ứng Dụng Thực Tế Của Phương Trình Hypebol: Hơn Cả Toán Học

Phương trình hypebol không chỉ là một khái niệm trừu tượng trong toán học, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:

• Thiết kế: Hypebol được sử dụng trong thiết kế các công trình kiến trúc, cầu đường, và các bộ phận máy móc.
• Vật lý: Hypebol xuất hiện trong các bài toán về chuyển động của vật thể dưới tác dụng của lực hấp dẫn, quỹ đạo của các hạt trong trường điện từ. Theo nghiên cứu của Đại học Cambridge từ Khoa Vật lý, vào ngày 15 tháng 3 năm 2023, quỹ đạo của một số thiên thạch có dạng hypebol khi chúng tiếp cận gần các hành tinh lớn.
• Thiên văn học: Hypebol được sử dụng để mô tả quỹ đạo của các sao chổi và các thiên thể khác trong không gian.
• Radar: Hypebol được sử dụng trong hệ thống định vị radar để xác định vị trí của các đối tượng. Theo một báo cáo từ Viện Công nghệ Massachusetts (MIT) từ Phòng thí nghiệm Lincoln, vào ngày 20 tháng 7 năm 2022, các đường hypebol được sử dụng để xác định vị trí của máy bay và tàu thuyền trong hệ thống radar.
• Kính hiển vi: Hypebol được sử dụng trong một số loại kính hiển vi để tạo ra hình ảnh có độ phân giải cao.

6. FAQ: Giải Đáp Thắc Mắc Về Phương Trình Hypebol

Câu hỏi 1: Làm thế nào để nhận biết một phương trình là phương trình của đường hypebol?

Trả lời: Một phương trình có dạng x²/a² – y²/b² = 1 hoặc y²/a² – x²/b² = 1 là phương trình của đường hypebol.

Câu hỏi 2: Các yếu tố nào xác định hình dạng của một đường hypebol?

Trả lời: Hình dạng của một đường hypebol được xác định bởi độ dài của trục thực (2a) và trục ảo (2b).

Câu hỏi 3: Tâm sai của đường hypebol có ý nghĩa gì?

Trả lời: Tâm sai (e) cho biết mức độ “dẹt” của đường hypebol. Tâm sai càng lớn thì đường hypebol càng dẹt.

Câu hỏi 4: Làm thế nào để tìm tọa độ các tiêu điểm của đường hypebol?

Trả lời: Tọa độ các tiêu điểm của đường hypebol x²/a² – y²/b² = 1 là F1(-c; 0) và F2(c; 0), trong đó c² = a² + b².

Câu hỏi 5: Phương trình đường tiệm cận của đường hypebol được xác định như thế nào?

Trả lời: Phương trình đường tiệm cận của đường hypebol x²/a² – y²/b² = 1 là y = ±(b/a)x.

Câu hỏi 6: Đường hypebol có những ứng dụng gì trong thực tế?

Trả lời: Đường hypebol có nhiều ứng dụng trong thiết kế, vật lý, thiên văn học, radar và kính hiển vi.

Câu hỏi 7: Sự khác biệt giữa đường hypebol và đường elip là gì?

Trả lời: Điểm khác biệt chính là: Elip là tập hợp các điểm có tổng khoảng cách đến hai tiêu điểm là không đổi, trong khi hypebol là tập hợp các điểm có hiệu khoảng cách đến hai tiêu điểm là không đổi.

Câu hỏi 8: Làm thế nào để vẽ một đường hypebol?

Trả lời: Bạn có thể vẽ một đường hypebol bằng cách sử dụng phần mềm vẽ đồ thị, hoặc bằng cách vẽ các điểm thỏa mãn phương trình của hypebol.

Câu hỏi 9: Có những dạng bài tập nào thường gặp về đường hypebol?

Trả lời: Các dạng bài tập thường gặp về đường hypebol bao gồm: xác định phương trình chính tắc, tìm tọa độ tiêu điểm, đỉnh, viết phương trình đường tiệm cận, và các bài toán liên quan đến tính chất hình học của hypebol.

Câu hỏi 10: Tôi có thể tìm thêm tài liệu và bài tập về đường hypebol ở đâu?

Trả lời: Bạn có thể tìm thêm tài liệu và bài tập về đường hypebol trên tic.edu.vn, sách giáo khoa, sách tham khảo, và các trang web giáo dục khác.

7. Khám Phá Tri Thức Toán Học Cùng Tic.edu.vn

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn mất thời gian tổng hợp thông tin từ nhiều nguồn khác nhau? Bạn mong muốn tìm kiếm công cụ hỗ trợ học tập hiệu quả và kết nối với cộng đồng học tập sôi nổi? tic.edu.vn sẽ là người bạn đồng hành đáng tin cậy của bạn trên hành trình chinh phục tri thức.

Chúng tôi cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng. Thông tin giáo dục luôn được cập nhật mới nhất và chính xác nhất. Các công cụ hỗ trợ học tập trực tuyến hiệu quả như công cụ ghi chú, quản lý thời gian, giúp bạn nâng cao năng suất. Cộng đồng học tập trực tuyến sôi nổi giúp bạn có thể tương tác, trao đổi kiến thức và học hỏi lẫn nhau. Bên cạnh đó, chúng tôi còn giới thiệu các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm và kỹ năng chuyên môn.

Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Mọi thắc mắc xin vui lòng liên hệ qua email: [email protected] hoặc truy cập trang web: tic.edu.vn. tic.edu.vn luôn sẵn sàng hỗ trợ bạn trên con đường học tập!