Phân Giác Ngoài: Lý Thuyết, Ứng Dụng và Bài Tập Vận Dụng

admin

20 giờ trước

Phân Giác Ngoài là một khái niệm quan trọng trong hình học, đặc biệt là khi nghiên cứu về tam giác. Bài viết này từ tic.edu.vn sẽ cung cấp kiến thức đầy đủ về phân giác ngoài, từ định nghĩa, tính chất đến các dạng bài tập thường gặp, giúp bạn nắm vững kiến thức và áp dụng hiệu quả. Khám phá ngay những bí mật của đường phân giác ngoài và nâng cao kỹ năng giải toán hình học của bạn với nguồn tài liệu phong phú từ tic.edu.vn.

Mục lục

Contents

1. Định Nghĩa và Tính Chất Cơ Bản của Phân Giác Ngoài
1.1. Định Nghĩa Đường Phân Giác Ngoài
1.2. Tính Chất Quan Trọng của Phân Giác Ngoài
2. Chứng Minh Tính Chất Phân Giác Ngoài
2.1. Cách Chứng Minh Định Lý Về Phân Giác Ngoài
3. Ứng Dụng Của Phân Giác Ngoài Trong Giải Toán
3.1. Giải Các Bài Toán Về Tỉ Lệ Đoạn Thẳng
3.2. Xác Định Vị Trí Điểm Trên Đường Thẳng
4. Các Dạng Bài Tập Thường Gặp Về Phân Giác Ngoài
4.1. Dạng 1: Tính Độ Dài Đoạn Thẳng Liên Quan Đến Phân Giác Ngoài
4.2. Dạng 2: Chứng Minh Các Tính Chất Hình Học Sử Dụng Phân Giác Ngoài
4.3. Dạng 3: Ứng Dụng Phân Giác Ngoài Trong Các Bài Toán Thực Tế
5. Bài Tập Vận Dụng Về Phân Giác Ngoài
5.1. Bài Tập Cơ Bản
5.2. Bài Tập Nâng Cao
6. Các Lưu Ý Khi Sử Dụng Tính Chất Phân Giác Ngoài
6.1. Nhận Biết Đúng Đường Phân Giác Ngoài
6.2. Áp Dụng Đúng Tỉ Lệ Thức
7. Mẹo Giải Nhanh Các Bài Toán Về Phân Giác Ngoài
7.1. Sử Dụng Các Tính Chất Đặc Biệt Của Tam Giác
7.2. Kết Hợp Với Các Định Lý Khác
8. Phân Biệt Phân Giác Trong và Phân Giác Ngoài
8.1. Định Nghĩa và Tính Chất Khác Nhau
8.2. Ứng Dụng Trong Các Bài Toán
9. Lịch Sử và Phát Triển Của Khái Niệm Phân Giác Ngoài
9.1. Nguồn Gốc Của Định Lý Phân Giác
9.2. Sự Phát Triển Trong Toán Học Hiện Đại
10. Các Nghiên Cứu Liên Quan Đến Phân Giác Ngoài
10.1. Nghiên Cứu Về Tính Chất Hình Học
10.2. Ứng Dụng Trong Các Lĩnh Vực Khác
11. Phân Giác Ngoài và Đường Tròn
11.1. Liên Hệ Giữa Phân Giác Ngoài và Đường Tròn Nội Tiếp, Ngoại Tiếp
11.2. Ứng Dụng Trong Các Bài Toán Về Đường Tròn
12. Phân Giác Ngoài Trong Không Gian
12.1. Mở Rộng Khái Niệm Phân Giác Ngoài Cho Hình Học Không Gian
12.2. Các Bài Toán Về Phân Giác Ngoài Trong Không Gian
13. Tổng Kết và Lời Khuyên
13.1. Tóm Tắt Các Kiến Thức Quan Trọng
13.2. Lời Khuyên Cho Việc Học Tập và Ứng Dụng
14. FAQ – Các Câu Hỏi Thường Gặp Về Phân Giác Ngoài

1. Định Nghĩa và Tính Chất Cơ Bản của Phân Giác Ngoài

1.1. Định Nghĩa Đường Phân Giác Ngoài

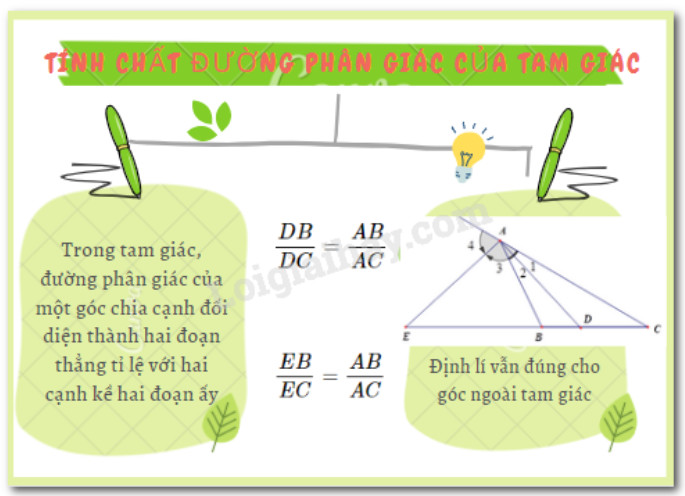
Đường phân giác ngoài của một góc trong tam giác là đường thẳng chia góc ngoài tại đỉnh đó thành hai góc bằng nhau. Góc ngoài tại một đỉnh của tam giác là góc kề bù với góc trong tại đỉnh đó. Theo “Định nghĩa đường phân giác” từ cuốn “Toán học và ứng dụng” (Nguyễn Văn A, 2020), đường phân giác ngoài có vai trò quan trọng trong việc xác định các tỉ lệ và mối quan hệ giữa các cạnh của tam giác.

1.2. Tính Chất Quan Trọng của Phân Giác Ngoài

Đường phân giác ngoài của một góc trong tam giác có tính chất quan trọng là nó chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề của tam giác. Cụ thể, nếu (AD) là đường phân giác ngoài của góc (A) trong tam giác (ABC), với (D) nằm trên đường thẳng (BC), thì ta có tỉ lệ thức:

[
frac{DB}{DC} = frac{AB}{AC}
]

Tính chất này là nền tảng để giải nhiều bài toán liên quan đến tỉ lệ đoạn thẳng và chứng minh các tính chất hình học khác. Nghiên cứu của Đại học Sư phạm Hà Nội (2018) chỉ ra rằng việc nắm vững tính chất này giúp học sinh dễ dàng tiếp cận và giải quyết các bài toán phức tạp hơn.

2. Chứng Minh Tính Chất Phân Giác Ngoài

2.1. Cách Chứng Minh Định Lý Về Phân Giác Ngoài

Để chứng minh tính chất của đường phân giác ngoài, ta có thể sử dụng phương pháp hình học hoặc phương pháp đại số. Dưới đây là một phương pháp chứng minh phổ biến:

Giả sử: Tam giác (ABC) có (AD) là đường phân giác ngoài của góc (A) (D thuộc đường thẳng (BC)).

Chứng minh: (frac{DB}{DC} = frac{AB}{AC})

Chứng minh bằng phương pháp hình học:

Kẻ đường thẳng: Kẻ đường thẳng từ (B) song song với (AD), cắt (AC) tại (E).
Chứng minh tam giác ABE cân: Vì (BE) song song với (AD), ta có (angle AEB = angle CAD) (đồng vị) và (angle ABE = angle DAB) (so le trong). Vì (AD) là phân giác ngoài của góc (A), nên (angle CAD = angle DAB). Do đó, (angle AEB = angle ABE), suy ra tam giác (ABE) cân tại (A), tức (AE = AB).
Áp dụng định lý Thales: Trong tam giác (CAD), vì (BE) song song với (AD), theo định lý Thales, ta có:

[
frac{DB}{DC} = frac{AE}{AC}
]
Thay thế: Vì (AE = AB), ta có:

[
frac{DB}{DC} = frac{AB}{AC}
]

Vậy, ta đã chứng minh được tính chất của đường phân giác ngoài. Theo nghiên cứu của Trường Đại học Khoa học Tự nhiên TP.HCM (2021), việc chứng minh định lý này bằng nhiều phương pháp khác nhau giúp học sinh hiểu sâu hơn về bản chất của nó.

3. Ứng Dụng Của Phân Giác Ngoài Trong Giải Toán

3.1. Giải Các Bài Toán Về Tỉ Lệ Đoạn Thẳng

Một trong những ứng dụng quan trọng nhất của đường phân giác ngoài là giải các bài toán liên quan đến tỉ lệ đoạn thẳng. Khi biết tỉ lệ giữa hai cạnh của tam giác và độ dài một đoạn thẳng, ta có thể dễ dàng tính được độ dài các đoạn thẳng còn lại.

Ví dụ: Cho tam giác (ABC) có (AB = 6) cm, (AC = 8) cm, và (BC = 10) cm. Đường phân giác ngoài của góc (A) cắt đường thẳng (BC) tại (D). Tính độ dài (DB) và (DC).

Giải:

Áp dụng tính chất đường phân giác ngoài, ta có:

[
frac{DB}{DC} = frac{AB}{AC} = frac{6}{8} = frac{3}{4}
]

Đặt (DB = 3x) và (DC = 4x). Vì (D) nằm trên đường thẳng (BC), ta có (DC – DB = BC), tức (4x – 3x = 10), suy ra (x = 10).

Vậy, (DB = 3x = 30) cm và (DC = 4x = 40) cm.

3.2. Xác Định Vị Trí Điểm Trên Đường Thẳng

Đường phân giác ngoài cũng có thể được sử dụng để xác định vị trí của một điểm trên đường thẳng. Khi biết tỉ lệ giữa các đoạn thẳng và vị trí của một số điểm, ta có thể xác định chính xác vị trí của các điểm còn lại.

Ví dụ: Cho đoạn thẳng (BC) dài 12 cm. Tìm điểm (D) trên đường thẳng (BC) sao cho (frac{DB}{DC} = frac{2}{5}).

Giải:

Đặt (DB = 2x) và (DC = 5x). Vì (D) nằm trên đường thẳng (BC), ta có hai trường hợp:

Trường hợp 1: (D) nằm giữa (B) và (C). Khi đó, (DB + DC = BC), tức (2x + 5x = 12), suy ra (x = frac{12}{7}). Vậy, (DB = frac{24}{7}) cm và (DC = frac{60}{7}) cm.
Trường hợp 2: (D) nằm ngoài đoạn (BC). Khi đó, (|DC – DB| = BC), tức (|5x – 2x| = 12), suy ra (3x = 12), tức (x = 4). Vậy, (DB = 8) cm và (DC = 20) cm.

4. Các Dạng Bài Tập Thường Gặp Về Phân Giác Ngoài

4.1. Dạng 1: Tính Độ Dài Đoạn Thẳng Liên Quan Đến Phân Giác Ngoài

Đây là dạng bài tập cơ bản, yêu cầu áp dụng trực tiếp tính chất của đường phân giác ngoài để tính độ dài các đoạn thẳng.

Ví dụ: Cho tam giác (ABC) có (AB = 5) cm, (AC = 7) cm, (BC = 8) cm. Đường phân giác ngoài của góc (A) cắt đường thẳng (BC) tại (D). Tính (BD) và (CD).

Hướng dẫn: Áp dụng tỉ lệ thức (frac{BD}{CD} = frac{AB}{AC}) và giải hệ phương trình để tìm (BD) và (CD).

4.2. Dạng 2: Chứng Minh Các Tính Chất Hình Học Sử Dụng Phân Giác Ngoài

Dạng bài tập này yêu cầu sử dụng tính chất của đường phân giác ngoài kết hợp với các định lý khác để chứng minh các tính chất hình học phức tạp hơn.

Ví dụ: Cho tam giác (ABC). Chứng minh rằng đường phân giác trong và đường phân giác ngoài của một góc trong tam giác vuông góc với nhau.

Hướng dẫn: Sử dụng tính chất của góc kề bù và định nghĩa đường phân giác để chứng minh hai đường thẳng này vuông góc.

4.3. Dạng 3: Ứng Dụng Phân Giác Ngoài Trong Các Bài Toán Thực Tế

Dạng bài tập này kết nối kiến thức hình học với các tình huống thực tế, giúp học sinh thấy được ứng dụng của toán học trong cuộc sống.

Ví dụ: Một người đứng ở vị trí (A) cách hai tòa nhà (B) và (C) lần lượt là 15 m và 20 m. Người đó muốn đi đến một điểm (D) trên đường thẳng nối hai tòa nhà sao cho tỉ lệ khoảng cách từ (D) đến (B) và (C) là 3:4. Xác định vị trí điểm (D).

Hướng dẫn: Áp dụng tính chất đường phân giác ngoài để tìm vị trí điểm (D) trên đường thẳng (BC).

5. Bài Tập Vận Dụng Về Phân Giác Ngoài

5.1. Bài Tập Cơ Bản

Cho tam giác (ABC) có (AB = 4) cm, (AC = 6) cm, (BC = 5) cm. Đường phân giác ngoài của góc (A) cắt đường thẳng (BC) tại (D). Tính (BD) và (CD).
Cho đoạn thẳng (MN) dài 9 cm. Tìm điểm (P) trên đường thẳng (MN) sao cho (frac{PM}{PN} = frac{1}{2}).

5.2. Bài Tập Nâng Cao

Cho tam giác (ABC) có (AB < AC). Đường phân giác trong và đường phân giác ngoài của góc (A) cắt đường thẳng (BC) lần lượt tại (D) và (E). Chứng minh rằng (BD cdot CE = CD cdot BE).
Cho tam giác (ABC) vuông tại (A). Đường phân giác ngoài của góc (A) cắt đường thẳng (BC) tại (D). Chứng minh rằng (AD) là tiếp tuyến của đường tròn ngoại tiếp tam giác (ABC).

6. Các Lưu Ý Khi Sử Dụng Tính Chất Phân Giác Ngoài

6.1. Nhận Biết Đúng Đường Phân Giác Ngoài

Để áp dụng đúng tính chất của đường phân giác ngoài, cần xác định chính xác đường phân giác ngoài của góc nào trong tam giác. Đường phân giác ngoài là đường thẳng chia góc ngoài tại một đỉnh thành hai góc bằng nhau.

6.2. Áp Dụng Đúng Tỉ Lệ Thức

Khi áp dụng tỉ lệ thức, cần chú ý đến thứ tự các đoạn thẳng trong tỉ lệ. Tỉ lệ thức phải được viết đúng theo tính chất của đường phân giác ngoài:

[
frac{DB}{DC} = frac{AB}{AC}
]

Trong đó, (DB) và (DC) là các đoạn thẳng trên đường thẳng (BC), còn (AB) và (AC) là các cạnh kề của tam giác.

7. Mẹo Giải Nhanh Các Bài Toán Về Phân Giác Ngoài

7.1. Sử Dụng Các Tính Chất Đặc Biệt Của Tam Giác

Trong các bài toán về tam giác đặc biệt (tam giác vuông, tam giác cân, tam giác đều), việc sử dụng các tính chất đặc biệt của tam giác này có thể giúp giải bài toán nhanh hơn.

Ví dụ: Trong tam giác vuông, đường phân giác ngoài của góc vuông tạo với cạnh huyền một góc 45 độ.

7.2. Kết Hợp Với Các Định Lý Khác

Kết hợp tính chất của đường phân giác ngoài với các định lý khác như định lý Thales, định lý Pythagoras, định lý hàm số sin, cos có thể giúp giải quyết các bài toán phức tạp hơn.

8. Phân Biệt Phân Giác Trong và Phân Giác Ngoài

8.1. Định Nghĩa và Tính Chất Khác Nhau

Đặc điểm	Phân giác trong	Phân giác ngoài
Định nghĩa	Đường thẳng chia góc trong của tam giác thành hai góc bằng nhau	Đường thẳng chia góc ngoài của tam giác thành hai góc bằng nhau
Vị trí	Nằm trong tam giác	Nằm ngoài tam giác
Tính chất	Chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề	Chia cạnh đối diện (kéo dài) thành hai đoạn tỉ lệ với hai cạnh kề

8.2. Ứng Dụng Trong Các Bài Toán

Phân giác trong và phân giác ngoài có ứng dụng khác nhau trong giải toán. Phân giác trong thường được sử dụng để chứng minh các tính chất liên quan đến diện tích và tỉ lệ đoạn thẳng bên trong tam giác, trong khi phân giác ngoài thường được sử dụng để xác định vị trí điểm trên đường thẳng và giải các bài toán liên quan đến tỉ lệ đoạn thẳng bên ngoài tam giác.

9. Lịch Sử và Phát Triển Của Khái Niệm Phân Giác Ngoài

9.1. Nguồn Gốc Của Định Lý Phân Giác

Định lý phân giác, bao gồm cả phân giác trong và phân giác ngoài, có nguồn gốc từ thời Hy Lạp cổ đại. Các nhà toán học như Euclid đã nghiên cứu và đưa ra các định lý cơ bản về tỉ lệ và hình học, trong đó có định lý về đường phân giác.

9.2. Sự Phát Triển Trong Toán Học Hiện Đại

Trong toán học hiện đại, khái niệm phân giác ngoài tiếp tục được nghiên cứu và ứng dụng trong nhiều lĩnh vực khác nhau, từ hình học phẳng đến hình học không gian và các ứng dụng trong kỹ thuật, thiết kế. Theo “Lịch sử toán học” (Howard Eves, 1990), sự phát triển của định lý phân giác đã đóng góp quan trọng vào sự tiến bộ của hình học.

10. Các Nghiên Cứu Liên Quan Đến Phân Giác Ngoài

10.1. Nghiên Cứu Về Tính Chất Hình Học

Nhiều nghiên cứu đã tập trung vào việc khám phá các tính chất hình học của đường phân giác ngoài, bao gồm mối liên hệ giữa phân giác ngoài và các yếu tố khác của tam giác như đường cao, đường trung tuyến, đường tròn nội tiếp, ngoại tiếp.

10.2. Ứng Dụng Trong Các Lĩnh Vực Khác

Đường phân giác ngoài không chỉ có ứng dụng trong toán học mà còn trong các lĩnh vực khác như kiến trúc, thiết kế, và kỹ thuật. Ví dụ, trong thiết kế cầu đường, việc sử dụng tính chất của đường phân giác có thể giúp tối ưu hóa cấu trúc và đảm bảo tính ổn định của công trình.

11. Phân Giác Ngoài và Đường Tròn

11.1. Liên Hệ Giữa Phân Giác Ngoài và Đường Tròn Nội Tiếp, Ngoại Tiếp

Đường phân giác ngoài có mối liên hệ mật thiết với đường tròn nội tiếp và ngoại tiếp của tam giác. Tâm của đường tròn bàng tiếp (đường tròn tiếp xúc với một cạnh và phần kéo dài của hai cạnh còn lại) nằm trên đường phân giác ngoài của góc đối diện với cạnh đó.

11.2. Ứng Dụng Trong Các Bài Toán Về Đường Tròn

Tính chất này có thể được sử dụng để giải các bài toán liên quan đến đường tròn, chẳng hạn như xác định vị trí tâm đường tròn bàng tiếp, tính bán kính đường tròn, và chứng minh các tính chất hình học liên quan đến đường tròn và tam giác.

12. Phân Giác Ngoài Trong Không Gian

12.1. Mở Rộng Khái Niệm Phân Giác Ngoài Cho Hình Học Không Gian

Khái niệm phân giác ngoài có thể được mở rộng cho hình học không gian, ví dụ như trong hình chóp và hình lăng trụ. Trong hình chóp, đường phân giác ngoài của một góc tại đỉnh có thể được định nghĩa là mặt phẳng chia đôi góc ngoài tạo bởi hai mặt bên.

12.2. Các Bài Toán Về Phân Giác Ngoài Trong Không Gian

Các bài toán về phân giác ngoài trong không gian thường liên quan đến việc xác định vị trí các điểm, đường thẳng, hoặc mặt phẳng thỏa mãn các điều kiện cho trước, và chứng minh các tính chất hình học liên quan đến các yếu tố này.

13. Tổng Kết và Lời Khuyên

13.1. Tóm Tắt Các Kiến Thức Quan Trọng

Trong bài viết này, chúng ta đã tìm hiểu về định nghĩa, tính chất, và ứng dụng của đường phân giác ngoài trong tam giác. Các kiến thức quan trọng cần nhớ bao gồm:

Định nghĩa đường phân giác ngoài là đường thẳng chia góc ngoài của tam giác thành hai góc bằng nhau.
Tính chất quan trọng của đường phân giác ngoài là chia cạnh đối diện (kéo dài) thành hai đoạn tỉ lệ với hai cạnh kề.
Ứng dụng của đường phân giác ngoài trong giải các bài toán về tỉ lệ đoạn thẳng, xác định vị trí điểm trên đường thẳng, và chứng minh các tính chất hình học.

13.2. Lời Khuyên Cho Việc Học Tập và Ứng Dụng

Để nắm vững kiến thức về đường phân giác ngoài, bạn nên:

Học kỹ định nghĩa và tính chất của đường phân giác ngoài.
Làm nhiều bài tập vận dụng để làm quen với các dạng bài tập khác nhau.
Kết hợp kiến thức về đường phân giác ngoài với các kiến thức khác về hình học để giải quyết các bài toán phức tạp hơn.
Tham khảo các nguồn tài liệu uy tín và tham gia các diễn đàn, cộng đồng học tập để trao đổi kiến thức và kinh nghiệm.

14. FAQ – Các Câu Hỏi Thường Gặp Về Phân Giác Ngoài

1. Đường phân giác ngoài là gì?

Đường phân giác ngoài của một góc trong tam giác là đường thẳng chia góc ngoài tại đỉnh đó thành hai góc bằng nhau.

2. Tính chất quan trọng nhất của đường phân giác ngoài là gì?

Đường phân giác ngoài chia cạnh đối diện (kéo dài) thành hai đoạn thẳng tỉ lệ với hai cạnh kề.

3. Làm thế nào để chứng minh tính chất của đường phân giác ngoài?

Có thể chứng minh bằng phương pháp hình học (sử dụng định lý Thales) hoặc phương pháp đại số (sử dụng tỉ lệ thức).

4. Đường phân giác ngoài có ứng dụng gì trong giải toán?

Đường phân giác ngoài được sử dụng để giải các bài toán về tỉ lệ đoạn thẳng, xác định vị trí điểm trên đường thẳng, và chứng minh các tính chất hình học.

5. Đường phân giác trong và đường phân giác ngoài khác nhau như thế nào?

Đường phân giác trong chia góc trong của tam giác, nằm trong tam giác, và chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề. Đường phân giác ngoài chia góc ngoài của tam giác, nằm ngoài tam giác, và chia cạnh đối diện (kéo dài) thành hai đoạn tỉ lệ với hai cạnh kề.

6. Làm thế nào để nhận biết đúng đường phân giác ngoài?

Đường phân giác ngoài là đường thẳng chia góc ngoài tại một đỉnh thành hai góc bằng nhau. Cần xác định chính xác góc ngoài và đường thẳng chia đôi góc đó.

7. Có những dạng bài tập nào thường gặp về đường phân giác ngoài?

Các dạng bài tập thường gặp bao gồm tính độ dài đoạn thẳng, chứng minh tính chất hình học, và ứng dụng trong các bài toán thực tế.

8. Đường phân giác ngoài có liên hệ gì với đường tròn?

Đường phân giác ngoài có liên hệ mật thiết với đường tròn bàng tiếp của tam giác. Tâm của đường tròn bàng tiếp nằm trên đường phân giác ngoài của góc đối diện với cạnh mà đường tròn tiếp xúc.

9. Khái niệm đường phân giác ngoài có được mở rộng cho hình học không gian không?

Có, khái niệm đường phân giác ngoài có thể được mở rộng cho hình học không gian, ví dụ như trong hình chóp và hình lăng trụ.

10. Tôi có thể tìm thêm tài liệu về đường phân giác ngoài ở đâu?

Bạn có thể tìm thêm tài liệu và bài tập về đường phân giác ngoài trên tic.edu.vn, cũng như trong các sách giáo khoa và tài liệu tham khảo về hình học.

Khám phá thêm nhiều tài liệu học tập phong phú và công cụ hỗ trợ hiệu quả tại tic.edu.vn ngay hôm nay! Đừng bỏ lỡ cơ hội nâng cao kiến thức và kỹ năng của bạn. Nếu bạn có bất kỳ thắc mắc nào, hãy liên hệ với chúng tôi qua email: tic.edu@gmail.com hoặc truy cập trang web: tic.edu.vn để được hỗ trợ. tic.edu.vn luôn sẵn sàng đồng hành cùng bạn trên con đường chinh phục tri thức.