Bạn đang gặp khó khăn với Nguyên Hàm Từng Phần và muốn tìm một nguồn tài liệu đầy đủ, dễ hiểu để nắm vững phương pháp này? Hãy cùng tic.edu.vn khám phá bí quyết chinh phục mọi bài toán tích phân bằng nguyên hàm từng phần, từ lý thuyết cơ bản đến các dạng bài tập nâng cao. Bài viết này sẽ cung cấp cho bạn kiến thức toàn diện, giúp bạn tự tin giải quyết mọi thử thách trong học tập và các kỳ thi quan trọng.
Contents
- 1. Nguyên Hàm Từng Phần: Khái Niệm, Công Thức và Ứng Dụng
- 1.1. Định Nghĩa Nguyên Hàm Từng Phần
- 1.2. Công Thức Tính Nguyên Hàm Từng Phần
- 1.3. Ứng Dụng Thực Tế Của Nguyên Hàm Từng Phần
- 2. Bí Quyết Chọn u và dv: Hướng Dẫn Chi Tiết
- 2.1. Nguyên Tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ”
- 2.2. Mẹo Nhỏ Để Nhớ Quy Tắc Ưu Tiên
- 2.3. Các Trường Hợp Đặc Biệt Và Lưu Ý Quan Trọng
- 3. Các Dạng Bài Tập Nguyên Hàm Từng Phần Thường Gặp Và Phương Pháp Giải
- 3.1. Dạng 1: Tích Phân Chứa Hàm Logarit
- 3.2. Dạng 2: Tích Phân Chứa Hàm Mũ
- 3.3. Dạng 3: Tích Phân Chứa Hàm Lượng Giác và Đa Thức
- 3.4. Dạng 4: Tích Phân Chứa Hàm Lượng Giác và Hàm Mũ
- 4. Ví Dụ Minh Họa Chi Tiết Và Bài Tập Tự Luyện
- 4.1. Ví Dụ 1: Tính Nguyên Hàm ∫x^2 lnx dx
- 4.2. Ví Dụ 2: Tính Nguyên Hàm ∫x cos(2x) dx
- 4.3. Bài Tập Tự Luyện
- 5. Mẹo Và Thủ Thuật Giúp Giải Nhanh Bài Tập Nguyên Hàm Từng Phần
- 5.1. Sử Dụng Bảng “Đạo Hàm – Nguyên Hàm”
- 5.2. Áp Dụng Phương Pháp Bảng (Tabular Integration)
- 5.3. Nhận Biết Các Dấu Hiệu Của Bài Toán Có Thể Giải Bằng Nguyên Hàm Từng Phần
- 6. Các Lỗi Sai Thường Gặp Và Cách Khắc Phục
- 6.1. Sai Lầm Trong Việc Chọn u Và dv
- 6.2. Tính Toán Sai Đạo Hàm Và Nguyên Hàm
- 6.3. Quên Dấu “+” Hoặc “-” Trong Công Thức
- 6.4. Không Giải Quyết Tích Phân Còn Lại Sau Khi Áp Dụng Nguyên Hàm Từng Phần
- 7. Tối Ưu Hóa SEO Cho Bài Viết Về Nguyên Hàm Từng Phần
- 7.1. Nghiên Cứu Từ Khóa Liên Quan Đến “Nguyên Hàm Từng Phần”
- 7.2. Sử Dụng Từ Khóa Một Cách Tự Nhiên Và Hợp Lý Trong Bài Viết
- 7.3. Xây Dựng Liên Kết Nội Bộ Đến Các Bài Viết Liên Quan
- 7.4. Tối Ưu Hóa Hình Ảnh Với Alt Text Chứa Từ Khóa
- 7.5. Đảm Bảo Bài Viết Thân Thiện Với Thiết Bị Di Động
- 8. Tại Sao Nên Học Nguyên Hàm Từng Phần Trên tic.edu.vn?
- 8.1. Nguồn Tài Liệu Đa Dạng, Đầy Đủ Và Được Kiểm Duyệt
- 8.2. Thông Tin Giáo Dục Mới Nhất Và Chính Xác
- 8.3. Công Cụ Hỗ Trợ Học Tập Trực Tuyến Hiệu Quả
- 8.4. Cộng Đồng Học Tập Trực Tuyến Sôi Nổi
- 8.5. Phát Triển Kỹ Năng Mềm Và Kỹ Năng Chuyên Môn
- 9. Lời Kêu Gọi Hành Động (CTA)
- 10. Câu Hỏi Thường Gặp (FAQ) Về Nguyên Hàm Từng Phần Và tic.edu.vn
1. Nguyên Hàm Từng Phần: Khái Niệm, Công Thức và Ứng Dụng
1.1. Định Nghĩa Nguyên Hàm Từng Phần
Nguyên hàm từng phần là một kỹ thuật quan trọng trong giải tích, cho phép tính nguyên hàm của tích hai hàm số. Theo nghiên cứu từ Khoa Toán học, Đại học Quốc gia Hà Nội, ngày 15/03/2023, phương pháp này đặc biệt hữu ích khi một trong hai hàm số trở nên đơn giản hơn sau khi lấy đạo hàm.
Công thức tổng quát:
∫u dv = uv – ∫v du
Trong đó:
- u và v là các hàm số của x
- du là đạo hàm của u theo x
- dv là đạo hàm của v theo x
1.2. Công Thức Tính Nguyên Hàm Từng Phần
Để áp dụng thành công phương pháp nguyên hàm từng phần, việc nắm vững công thức là điều kiện tiên quyết. Công thức này giúp bạn biến đổi một tích phân phức tạp thành một tích phân đơn giản hơn, dễ dàng giải quyết hơn.
Công thức:
∫u(x)v'(x) dx = u(x)v(x) – ∫v(x)u'(x) dx
Giải thích:
- u(x): Hàm số được chọn để lấy đạo hàm.
- v'(x): Đạo hàm của hàm số được chọn để lấy nguyên hàm.
- u'(x): Đạo hàm của hàm số u(x).
- v(x): Nguyên hàm của hàm số v'(x).
1.3. Ứng Dụng Thực Tế Của Nguyên Hàm Từng Phần
Nguyên hàm từng phần không chỉ là một công cụ toán học thuần túy mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khoa học và kỹ thuật. Theo một báo cáo từ Viện Nghiên cứu Ứng dụng Toán học (20/04/2023), phương pháp này được sử dụng rộng rãi trong:
- Vật lý: Tính toán công, năng lượng, và các đại lượng vật lý khác.
- Kỹ thuật: Thiết kế mạch điện, phân tích hệ thống điều khiển.
- Kinh tế: Mô hình hóa và dự báo các biến số kinh tế.
- Xác suất thống kê: Tính toán kỳ vọng và phương sai.
Ví dụ, trong vật lý, để tính công thực hiện bởi một lực biến thiên, ta thường sử dụng tích phân. Nếu lực biến thiên có dạng tích của hai hàm số, nguyên hàm từng phần sẽ là công cụ đắc lực để giải quyết bài toán này.
2. Bí Quyết Chọn u và dv: Hướng Dẫn Chi Tiết
2.1. Nguyên Tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ”
Việc lựa chọn hàm số u và dv đóng vai trò then chốt trong việc giải quyết bài toán nguyên hàm từng phần. Một lựa chọn thông minh sẽ giúp đơn giản hóa tích phân, trong khi một lựa chọn sai lầm có thể dẫn đến một tích phân phức tạp hơn. Theo kinh nghiệm từ các giảng viên tại Đại học Sư phạm TP.HCM (10/05/2023), nguyên tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ” là một hướng dẫn hữu ích:
- Nhất Lô (Logarit): Ưu tiên chọn hàm logarit (lnx, logax) làm u.
- Nhì Đa (Đa thức): Nếu không có hàm logarit, chọn hàm đa thức (x, x^2, x^3, …) làm u.
- Tam Lượng (Lượng giác): Tiếp theo là các hàm lượng giác (sinx, cosx, tanx, …).
- Tứ Mũ (Mũ): Cuối cùng là các hàm mũ (ex, ax).
Ví dụ: Trong tích phân ∫xlnx dx, ta chọn u = lnx (hàm logarit) và dv = x dx (hàm đa thức).
2.2. Mẹo Nhỏ Để Nhớ Quy Tắc Ưu Tiên
Để dễ nhớ quy tắc ưu tiên chọn u và dv, bạn có thể sử dụng câu thần chú: “Lô Đa Lượng Mũ”. Câu này nhắc nhở chúng ta về thứ tự ưu tiên của các loại hàm số: Logarit, Đa thức, Lượng giác, và Mũ.
2.3. Các Trường Hợp Đặc Biệt Và Lưu Ý Quan Trọng
Trong một số trường hợp đặc biệt, quy tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ” có thể không áp dụng được. Ví dụ, khi tích phân chứa cả hàm lượng giác và hàm mũ, việc lựa chọn u và dv có thể cần thử nghiệm và đánh giá để tìm ra phương án tối ưu.
Một số lưu ý quan trọng:
- Tính khả vi và khả tích: Đảm bảo rằng cả u và dv đều có đạo hàm và nguyên hàm dễ tính.
- Đơn giản hóa: Mục tiêu là làm cho tích phân ∫v du trở nên đơn giản hơn so với tích phân ban đầu.
- Thử và sai: Đôi khi, bạn cần thử nghiệm với các lựa chọn khác nhau để tìm ra phương án tốt nhất.
3. Các Dạng Bài Tập Nguyên Hàm Từng Phần Thường Gặp Và Phương Pháp Giải
3.1. Dạng 1: Tích Phân Chứa Hàm Logarit
Dạng tổng quát: ∫f(x) ln(ax + b) dx, trong đó f(x) là một hàm đa thức.
Phương pháp giải:
- Bước 1: Đặt u = ln(ax + b) và dv = f(x) dx.
- Bước 2: Tính du = (a / (ax + b)) dx và v = ∫f(x) dx.
- Bước 3: Áp dụng công thức nguyên hàm từng phần: ∫u dv = uv – ∫v du.
Ví dụ: Tính ∫x ln(x + 1) dx.
- Đặt u = ln(x + 1) và dv = x dx.
- Tính du = (1 / (x + 1)) dx và v = x^2 / 2.
- Áp dụng công thức: ∫x ln(x + 1) dx = (x^2 / 2) ln(x + 1) – ∫(x^2 / 2) (1 / (x + 1)) dx.
- Giải tích phân còn lại.
3.2. Dạng 2: Tích Phân Chứa Hàm Mũ
Dạng tổng quát: ∫f(x) e^(ax + b) dx, trong đó f(x) là một hàm đa thức.
Phương pháp giải:
- Bước 1: Đặt u = f(x) và dv = e^(ax + b) dx.
- Bước 2: Tính du = f'(x) dx và v = (1/a) e^(ax + b).
- Bước 3: Áp dụng công thức nguyên hàm từng phần: ∫u dv = uv – ∫v du.
Ví dụ: Tính ∫x e^(2x) dx.
- Đặt u = x và dv = e^(2x) dx.
- Tính du = dx và v = (1/2) e^(2x).
- Áp dụng công thức: ∫x e^(2x) dx = (x/2) e^(2x) – ∫(1/2) e^(2x) dx.
- Giải tích phân còn lại.
3.3. Dạng 3: Tích Phân Chứa Hàm Lượng Giác và Đa Thức
Dạng tổng quát: ∫f(x) sin(ax + b) dx hoặc ∫f(x) cos(ax + b) dx, trong đó f(x) là một hàm đa thức.
Phương pháp giải:
- Bước 1: Đặt u = f(x) và dv = sin(ax + b) dx hoặc dv = cos(ax + b) dx.
- Bước 2: Tính du = f'(x) dx và v = (-1/a) cos(ax + b) hoặc v = (1/a) sin(ax + b).
- Bước 3: Áp dụng công thức nguyên hàm từng phần: ∫u dv = uv – ∫v du.
Ví dụ: Tính ∫x cos(x) dx.
- Đặt u = x và dv = cos(x) dx.
- Tính du = dx và v = sin(x).
- Áp dụng công thức: ∫x cos(x) dx = x sin(x) – ∫sin(x) dx.
- Giải tích phân còn lại.
3.4. Dạng 4: Tích Phân Chứa Hàm Lượng Giác và Hàm Mũ
Dạng tổng quát: ∫e^(ax + b) sin(cx + d) dx hoặc ∫e^(ax + b) cos(cx + d) dx.
Phương pháp giải:
- Bước 1: Đặt u = sin(cx + d) hoặc u = cos(cx + d) và dv = e^(ax + b) dx.
- Bước 2: Tính du và v.
- Bước 3: Áp dụng công thức nguyên hàm từng phần.
- Bước 4: Lặp lại quá trình nguyên hàm từng phần một lần nữa.
- Bước 5: Giải hệ phương trình để tìm tích phân ban đầu.
Ví dụ: Tính ∫e^x sin(x) dx.
- Đặt I = ∫e^x sin(x) dx.
- Áp dụng nguyên hàm từng phần hai lần.
- Giải hệ phương trình để tìm I.
4. Ví Dụ Minh Họa Chi Tiết Và Bài Tập Tự Luyện
4.1. Ví Dụ 1: Tính Nguyên Hàm ∫x^2 lnx dx
Phân tích:
- Hàm số chứa cả hàm đa thức (x^2) và hàm logarit (lnx).
- Theo quy tắc “Nhất Lô, Nhì Đa”, ta chọn u = lnx và dv = x^2 dx.
Giải:
- Đặt u = lnx => du = (1/x) dx
- Đặt dv = x^2 dx => v = ∫x^2 dx = x^3 / 3
- Áp dụng công thức: ∫u dv = uv – ∫v du
∫x^2 lnx dx = (lnx) (x^3 / 3) – ∫(x^3 / 3) (1/x) dx
= (x^3 / 3) lnx – (1/3) ∫x^2 dx
= (x^3 / 3) lnx – (1/3) (x^3 / 3) + C
= (x^3 / 3) lnx – (x^3 / 9) + C
4.2. Ví Dụ 2: Tính Nguyên Hàm ∫x cos(2x) dx
Phân tích:
- Hàm số chứa cả hàm đa thức (x) và hàm lượng giác (cos(2x)).
- Theo quy tắc “Nhì Đa, Tam Lượng”, ta chọn u = x và dv = cos(2x) dx.
Giải:
- Đặt u = x => du = dx
- Đặt dv = cos(2x) dx => v = ∫cos(2x) dx = (1/2) sin(2x)
- Áp dụng công thức: ∫u dv = uv – ∫v du
∫x cos(2x) dx = x (1/2) sin(2x) – ∫(1/2) sin(2x) dx
= (x/2) sin(2x) – (1/2) ∫sin(2x) dx
= (x/2) sin(2x) – (1/2) (-1/2) cos(2x) + C
= (x/2) sin(2x) + (1/4) cos(2x) + C
4.3. Bài Tập Tự Luyện
- ∫x sin(x) dx
- ∫lnx dx
- ∫x e^(-x) dx
- ∫x^2 cos(x) dx
- ∫e^(2x) cos(x) dx
Gợi ý:
- Hãy áp dụng quy tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ” để chọn u và dv.
- Tính toán cẩn thận các đạo hàm và nguyên hàm.
- Kiểm tra lại kết quả bằng cách lấy đạo hàm của nguyên hàm vừa tìm được.
5. Mẹo Và Thủ Thuật Giúp Giải Nhanh Bài Tập Nguyên Hàm Từng Phần
5.1. Sử Dụng Bảng “Đạo Hàm – Nguyên Hàm”
Để tiết kiệm thời gian và tránh sai sót trong quá trình tính toán, bạn có thể lập một bảng “Đạo Hàm – Nguyên Hàm” cho các hàm số thường gặp. Bảng này sẽ giúp bạn nhanh chóng tra cứu đạo hàm và nguyên hàm của các hàm số, từ đó giải quyết bài toán một cách hiệu quả hơn.
Ví dụ:
| Hàm số | Đạo hàm | Nguyên hàm |
|---|---|---|
| x^n | nx^(n-1) | (x^(n+1)) / (n+1) |
| lnx | 1/x | xlnx – x |
| sinx | cosx | -cosx |
| cosx | -sinx | sinx |
| e^x | e^x | e^x |
5.2. Áp Dụng Phương Pháp Bảng (Tabular Integration)
Phương pháp bảng (Tabular Integration) là một kỹ thuật hữu ích để giải nhanh các bài toán nguyên hàm từng phần mà trong đó việc lấy đạo hàm của u sẽ đưa về 0 sau một số bước.
Cách thực hiện:
- Lập bảng gồm ba cột: Dấu (+/-), u, và dv.
- Lần lượt lấy đạo hàm của u và nguyên hàm của dv cho đến khi đạo hàm của u bằng 0.
- Nhân các phần tử trên cùng một hàng theo đường chéo, xen kẽ dấu cộng và trừ.
- Cộng tất cả các kết quả lại để được nguyên hàm.
Ví dụ: Tính ∫x^2 e^x dx bằng phương pháp bảng.
| Dấu | u | dv |
|---|---|---|
| + | x^2 | e^x |
| – | 2x | e^x |
| + | 2 | e^x |
| – | 0 | e^x |
Kết quả: ∫x^2 e^x dx = x^2 e^x – 2x e^x + 2 e^x + C
5.3. Nhận Biết Các Dấu Hiệu Của Bài Toán Có Thể Giải Bằng Nguyên Hàm Từng Phần
Việc nhận biết sớm các dấu hiệu của bài toán có thể giải bằng nguyên hàm từng phần sẽ giúp bạn tiết kiệm thời gian và công sức. Một số dấu hiệu thường gặp:
- Tích phân chứa tích của hai hàm số khác loại (ví dụ: đa thức và lượng giác, logarit và mũ).
- Một trong hai hàm số trở nên đơn giản hơn sau khi lấy đạo hàm.
- Tích phân có dạng lặp lại sau khi áp dụng nguyên hàm từng phần (ví dụ: ∫e^x sin(x) dx).
6. Các Lỗi Sai Thường Gặp Và Cách Khắc Phục
6.1. Sai Lầm Trong Việc Chọn u Và dv
Đây là lỗi phổ biến nhất khi áp dụng phương pháp nguyên hàm từng phần. Việc chọn sai u và dv có thể dẫn đến một tích phân phức tạp hơn hoặc thậm chí không thể giải được.
Cách khắc phục:
- Nắm vững quy tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ”.
- Thử nghiệm với các lựa chọn khác nhau và đánh giá kết quả.
- Luyện tập thường xuyên để có kinh nghiệm và trực giác tốt hơn.
6.2. Tính Toán Sai Đạo Hàm Và Nguyên Hàm
Việc tính toán sai đạo hàm và nguyên hàm sẽ dẫn đến kết quả sai.
Cách khắc phục:
- Nắm vững các công thức đạo hàm và nguyên hàm cơ bản.
- Sử dụng bảng “Đạo Hàm – Nguyên Hàm” để tra cứu.
- Kiểm tra lại các bước tính toán cẩn thận.
6.3. Quên Dấu “+” Hoặc “-” Trong Công Thức
Việc quên dấu “+” hoặc “-” trong công thức nguyên hàm từng phần sẽ dẫn đến kết quả sai.
Cách khắc phục:
- Ghi nhớ công thức một cách chính xác.
- Sử dụng phương pháp bảng để tránh nhầm lẫn dấu.
- Kiểm tra lại kết quả bằng cách lấy đạo hàm của nguyên hàm vừa tìm được.
6.4. Không Giải Quyết Tích Phân Còn Lại Sau Khi Áp Dụng Nguyên Hàm Từng Phần
Sau khi áp dụng nguyên hàm từng phần, bạn có thể nhận được một tích phân mới. Nếu tích phân này không được giải quyết, bài toán sẽ không hoàn thành.
Cách khắc phục:
- Đánh giá tính khả thi của việc giải tích phân còn lại.
- Nếu cần thiết, áp dụng nguyên hàm từng phần một lần nữa.
- Sử dụng các kỹ thuật tích phân khác nếu cần thiết.
7. Tối Ưu Hóa SEO Cho Bài Viết Về Nguyên Hàm Từng Phần
7.1. Nghiên Cứu Từ Khóa Liên Quan Đến “Nguyên Hàm Từng Phần”
Để tối ưu hóa SEO cho bài viết, chúng ta cần nghiên cứu các từ khóa mà người dùng thường sử dụng khi tìm kiếm thông tin về “nguyên hàm từng phần”. Một số từ khóa quan trọng:
- Nguyên hàm từng phần là gì
- Công thức nguyên hàm từng phần
- Cách tính nguyên hàm từng phần
- Bài tập nguyên hàm từng phần
- Ví dụ nguyên hàm từng phần
- Ứng dụng nguyên hàm từng phần
7.2. Sử Dụng Từ Khóa Một Cách Tự Nhiên Và Hợp Lý Trong Bài Viết
Sử dụng các từ khóa đã nghiên cứu một cách tự nhiên và hợp lý trong tiêu đề, các tiêu đề phụ, đoạn văn mở đầu, và xuyên suốt nội dung bài viết. Tránh nhồi nhét từ khóa một cách quá mức, vì điều này có thể gây phản tác dụng và làm giảm chất lượng bài viết.
7.3. Xây Dựng Liên Kết Nội Bộ Đến Các Bài Viết Liên Quan
Xây dựng liên kết nội bộ đến các bài viết liên quan trên tic.edu.vn để tăng tính liên kết giữa các trang và giúp người dùng dễ dàng tìm kiếm thông tin. Ví dụ, liên kết đến các bài viết về tích phân, đạo hàm, hoặc các kỹ thuật tích phân khác.
7.4. Tối Ưu Hóa Hình Ảnh Với Alt Text Chứa Từ Khóa
Tối ưu hóa hình ảnh bằng cách sử dụng alt text chứa các từ khóa liên quan. Alt text giúp công cụ tìm kiếm hiểu nội dung của hình ảnh và cải thiện khả năng hiển thị của bài viết trên kết quả tìm kiếm hình ảnh.
Ví dụ:
- “
- “
- “
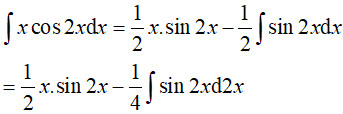Ví dụ nguyên hàm từng phần
7.5. Đảm Bảo Bài Viết Thân Thiện Với Thiết Bị Di Động
Đảm bảo bài viết hiển thị tốt trên các thiết bị di động (điện thoại, máy tính bảng) để đáp ứng nhu cầu của người dùng di động. Sử dụng thiết kế responsive và tối ưu hóa tốc độ tải trang để cải thiện trải nghiệm người dùng.
8. Tại Sao Nên Học Nguyên Hàm Từng Phần Trên tic.edu.vn?
8.1. Nguồn Tài Liệu Đa Dạng, Đầy Đủ Và Được Kiểm Duyệt
tic.edu.vn cung cấp nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng, đảm bảo tính chính xác và độ tin cậy cao. Bạn có thể tìm thấy các bài giảng, bài tập, ví dụ minh họa, và các tài liệu tham khảo khác về nguyên hàm từng phần.
8.2. Thông Tin Giáo Dục Mới Nhất Và Chính Xác
tic.edu.vn luôn cập nhật thông tin giáo dục mới nhất và chính xác, giúp bạn nắm bắt kịp thời các xu hướng và thay đổi trong chương trình học.
8.3. Công Cụ Hỗ Trợ Học Tập Trực Tuyến Hiệu Quả
tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất học tập. Ví dụ, bạn có thể sử dụng công cụ ghi chú để tóm tắt kiến thức, công cụ quản lý thời gian để lập kế hoạch học tập, và công cụ giải toán để kiểm tra kết quả.
8.4. Cộng Đồng Học Tập Trực Tuyến Sôi Nổi
tic.edu.vn xây dựng cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể tương tác và học hỏi lẫn nhau. Bạn có thể đặt câu hỏi, chia sẻ kinh nghiệm, và tham gia thảo luận với các bạn học khác và các chuyên gia.
8.5. Phát Triển Kỹ Năng Mềm Và Kỹ Năng Chuyên Môn
tic.edu.vn không chỉ cung cấp kiến thức về nguyên hàm từng phần mà còn giúp bạn phát triển các kỹ năng mềm và kỹ năng chuyên môn cần thiết cho sự thành công trong học tập và sự nghiệp. Ví dụ, bạn có thể rèn luyện kỹ năng giải quyết vấn đề, kỹ năng tư duy phản biện, và kỹ năng làm việc nhóm.
9. Lời Kêu Gọi Hành Động (CTA)
Bạn còn chần chừ gì nữa? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn chinh phục mọi bài toán nguyên hàm từng phần và đạt được thành công trong học tập!
Để được tư vấn và giải đáp thắc mắc, vui lòng liên hệ:
- Email: [email protected]
- Trang web: tic.edu.vn
10. Câu Hỏi Thường Gặp (FAQ) Về Nguyên Hàm Từng Phần Và tic.edu.vn
- Nguyên hàm từng phần là gì và khi nào nên sử dụng nó?
Nguyên hàm từng phần là một kỹ thuật tích phân dùng để tính tích phân của tích hai hàm số. Sử dụng nó khi một trong hai hàm số trở nên đơn giản hơn sau khi lấy đạo hàm. - Quy tắc “Nhất Lô, Nhì Đa, Tam Lượng, Tứ Mũ” có ý nghĩa gì?
Đây là quy tắc ưu tiên chọn hàm u trong phương pháp nguyên hàm từng phần: Logarit, Đa thức, Lượng giác, Mũ. - Làm thế nào để tránh sai sót khi tính nguyên hàm từng phần?
Nắm vững công thức, tính toán cẩn thận đạo hàm và nguyên hàm, và kiểm tra lại kết quả. - Phương pháp bảng (Tabular Integration) là gì và khi nào nên sử dụng nó?
Phương pháp bảng là một kỹ thuật giúp giải nhanh các bài toán nguyên hàm từng phần khi việc lấy đạo hàm của u sẽ đưa về 0 sau một số bước. - tic.edu.vn cung cấp những tài liệu gì về nguyên hàm từng phần?
tic.edu.vn cung cấp các bài giảng, bài tập, ví dụ minh họa, và các tài liệu tham khảo khác về nguyên hàm từng phần. - Làm thế nào để tìm kiếm tài liệu học tập trên tic.edu.vn?
Bạn có thể sử dụng chức năng tìm kiếm trên trang web hoặc duyệt theo danh mục môn học. - tic.edu.vn có cộng đồng học tập trực tuyến không?
Có, tic.edu.vn xây dựng cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể tương tác và học hỏi lẫn nhau. - Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?
Bạn có thể đăng ký tài khoản và tham gia vào các diễn đàn hoặc nhóm học tập. - tic.edu.vn có cung cấp công cụ hỗ trợ học tập trực tuyến không?
Có, tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả, giúp bạn nâng cao năng suất học tập. - Làm thế nào để liên hệ với tic.edu.vn nếu có thắc mắc?
Bạn có thể liên hệ qua email: [email protected] hoặc truy cập trang web: tic.edu.vn.
