Bạn đang tìm kiếm phương pháp tính Nguyên Hàm Của Tan một cách dễ dàng và hiệu quả? Bài viết này của tic.edu.vn sẽ cung cấp cho bạn công thức, ví dụ minh họa chi tiết và các bài tập vận dụng đa dạng, giúp bạn chinh phục mọi bài toán liên quan đến nguyên hàm của tan. Hãy cùng khám phá những kiến thức hữu ích này để nâng cao trình độ toán học của bạn.
Contents
- 1. Định Nghĩa Và Công Thức Tính Nguyên Hàm Của Tanx
- 2. Các Dạng Bài Tập Về Nguyên Hàm Của Tanx Thường Gặp
- 2.1. Tính Nguyên Hàm Trực Tiếp Của Hàm Số tanx
- 2.2. Tính Nguyên Hàm Của Các Hàm Số Lượng Giác Biến Đổi Về tanx
- 2.3. Sử Dụng Phương Pháp Tích Phân Từng Phần Với Hàm Số Chứa tanx
- 2.4. Bài Toán Ứng Dụng Nguyên Hàm Của tanx Trong Hình Học
- 2.5. Bài Toán Tìm Hàm Số Khi Biết Đạo Hàm Liên Quan Đến tanx
- 3. Mẹo Tính Nhanh Nguyên Hàm Của tanx Và Các Lưu Ý Quan Trọng
- 4. Ứng Dụng Của Nguyên Hàm tanx Trong Các Lĩnh Vực Khác
- 5. Các Nguồn Tài Liệu Tham Khảo Về Nguyên Hàm Của tanx Tại tic.edu.vn
- 6. Phân Tích Chi Tiết Các Ví Dụ Minh Họa Về Nguyên Hàm Của tanx
- 7. Các Bài Tập Nâng Cao Về Nguyên Hàm Của tanx Và Hướng Dẫn Giải
- 8. Các Lỗi Sai Thường Gặp Khi Tính Nguyên Hàm Của tanx Và Cách Khắc Phục
- 9. Tại Sao Nên Học Về Nguyên Hàm Của tanx Tại tic.edu.vn?
- 10. FAQ – Các Câu Hỏi Thường Gặp Về Nguyên Hàm Của tanx
1. Định Nghĩa Và Công Thức Tính Nguyên Hàm Của Tanx
Nguyên hàm của một hàm số f(x) là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x), tức là F'(x) = f(x). Việc tìm nguyên hàm là một trong những phép toán cơ bản và quan trọng trong giải tích.
Vậy, nguyên hàm của tanx là gì?
Trả lời: Nguyên hàm của tanx là -ln|cosx| + C, trong đó C là hằng số tích phân.
$int tanx dx = -ln|cosx| + C$
Giải thích chi tiết:
Công thức này có được bằng cách biến đổi tanx thành sinx/cosx và sử dụng phương pháp đổi biến số:
- Đặt u = cosx
- Khi đó du = -sinx dx
- Vậy $int tanx dx = int frac{sinx}{cosx} dx = -int frac{du}{u} = -ln|u| + C = -ln|cosx| + C$
Ứng dụng thực tế:
Công thức nguyên hàm của tanx được sử dụng rộng rãi trong các bài toán tích phân, tính diện tích, thể tích và giải các phương trình vi phân. Nắm vững công thức này sẽ giúp bạn giải quyết các bài toán một cách nhanh chóng và chính xác. Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, việc hiểu rõ công thức này giúp học sinh tăng 20% khả năng giải quyết các bài toán tích phân phức tạp.
2. Các Dạng Bài Tập Về Nguyên Hàm Của Tanx Thường Gặp
Để giúp bạn hiểu rõ hơn về cách áp dụng công thức nguyên hàm của tanx, chúng ta sẽ cùng nhau khám phá các dạng bài tập thường gặp và phương pháp giải quyết chúng. tic.edu.vn đã tổng hợp những dạng bài tập sau đây để bạn luyện tập:
2.1. Tính Nguyên Hàm Trực Tiếp Của Hàm Số tanx
Đây là dạng bài tập cơ bản nhất, yêu cầu bạn áp dụng trực tiếp công thức đã học để tìm nguyên hàm.
Ví dụ 1: Tính $int tan(2x+1) dx$
Giải:
- Đặt t = 2x + 1 => dt = 2dx => dx = dt/2
- Khi đó, $int tan(2x+1) dx = int tan(t) frac{dt}{2} = frac{1}{2} int tan(t) dt = -frac{1}{2}ln|cos(t)| + C = -frac{1}{2}ln|cos(2x+1)| + C$
Ví dụ 2: Tính $int 3tan(x/3) dx$
Giải:
- Đặt t = x/3 => dt = dx/3 => dx = 3dt
- Khi đó, $int 3tan(x/3) dx = int 3tan(t) 3dt = 9 int tan(t) dt = -9ln|cos(t)| + C = -9ln|cos(x/3)| + C$
2.2. Tính Nguyên Hàm Của Các Hàm Số Lượng Giác Biến Đổi Về tanx
Dạng bài tập này đòi hỏi bạn phải sử dụng các công thức lượng giác để biến đổi hàm số ban đầu về dạng tanx hoặc các hàm số có liên quan đến tanx, sau đó áp dụng công thức nguyên hàm.
Ví dụ 1: Tính $int frac{sin2x}{cos^{2}x} dx$
Giải:
- Ta có: $frac{sin2x}{cos^{2}x} = frac{2sinxcosx}{cos^{2}x} = 2tanx$
- Vậy, $int frac{sin2x}{cos^{2}x} dx = int 2tanx dx = -2ln|cosx| + C$
Ví dụ 2: Tính $int frac{1}{cosxsinx} dx$
Giải:
- Ta có: $frac{1}{cosxsinx} = frac{sin^{2}x + cos^{2}x}{cosxsinx} = frac{sinx}{cosx} + frac{cosx}{sinx} = tanx + cotx$
- Vậy, $int frac{1}{cosxsinx} dx = int (tanx + cotx) dx = -ln|cosx| + ln|sinx| + C = ln|frac{sinx}{cosx}| + C = ln|tanx| + C$
2.3. Sử Dụng Phương Pháp Tích Phân Từng Phần Với Hàm Số Chứa tanx
Trong một số trường hợp, bạn cần kết hợp phương pháp tích phân từng phần với công thức nguyên hàm của tanx để giải quyết bài toán.
Ví dụ: Tính $int x tanx dx$
Giải:
- Đặt u = x, dv = tanx dx
- => du = dx, v = -ln|cosx|
- Khi đó, $int x tanx dx = -xln|cosx| – int (-ln|cosx|) dx = -xln|cosx| + int ln|cosx| dx$
- Nguyên hàm $int ln|cosx| dx$ không có biểu thức sơ cấp, nên ta dừng lại ở đây.
2.4. Bài Toán Ứng Dụng Nguyên Hàm Của tanx Trong Hình Học
Nguyên hàm của tanx còn được ứng dụng để giải các bài toán liên quan đến tính diện tích hình phẳng giới hạn bởi các đường cong, trong đó có các đường biểu diễn hàm số lượng giác.
Ví dụ: Tính diện tích hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0 và x = $frac{pi}{4}$
Giải:
- Diện tích cần tìm là: $S = int{0}^{frac{pi}{4}} tanx dx = -ln|cosx| |{0}^{frac{pi}{4}} = -ln|cos(frac{pi}{4})| + ln|cos(0)| = -ln(frac{sqrt{2}}{2}) + ln(1) = -ln(frac{sqrt{2}}{2}) = ln(sqrt{2}) = frac{1}{2}ln2$
2.5. Bài Toán Tìm Hàm Số Khi Biết Đạo Hàm Liên Quan Đến tanx
Dạng bài tập này yêu cầu bạn tìm hàm số gốc khi biết đạo hàm của nó có chứa biểu thức tanx.
Ví dụ: Tìm hàm số f(x) biết f'(x) = $tan^{2}x$ và f(0) = 1
Giải:
- Ta có: $f(x) = int f'(x) dx = int tan^{2}x dx = int (frac{1}{cos^{2}x} – 1) dx = tanx – x + C$
- Vì f(0) = 1 => tan(0) – 0 + C = 1 => C = 1
- Vậy, f(x) = tanx – x + 1
3. Mẹo Tính Nhanh Nguyên Hàm Của tanx Và Các Lưu Ý Quan Trọng
Để giúp bạn tiết kiệm thời gian và nâng cao hiệu quả giải toán, tic.edu.vn xin chia sẻ một số mẹo tính nhanh và các lưu ý quan trọng khi tính nguyên hàm của tanx:
- Nhớ kỹ công thức gốc: $int tanx dx = -ln|cosx| + C$. Đây là chìa khóa để giải quyết mọi bài toán liên quan.
- Sử dụng công thức lượng giác: Biến đổi các biểu thức lượng giác phức tạp về dạng tanx hoặc các biểu thức đơn giản hơn.
- Áp dụng phương pháp đổi biến số: Khi gặp các hàm số tan(ax+b), hãy đặt t = ax+b để đưa về dạng cơ bản.
- Kiểm tra lại kết quả: Sau khi tính xong, hãy đạo hàm kết quả để xem có trùng với hàm số ban đầu hay không.
- Chú ý đến điều kiện xác định: Hàm số tanx không xác định tại các điểm x = $frac{pi}{2} + kpi$, do đó cần lưu ý khi tính tích phân trên các khoảng chứa các điểm này.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để làm quen với các dạng toán và rèn luyện kỹ năng.
Theo một khảo sát gần đây của tic.edu.vn, học sinh thường mắc lỗi khi quên công thức gốc hoặc không chú ý đến điều kiện xác định của hàm số. Hãy cẩn thận và ghi nhớ những điều này để tránh sai sót không đáng có.
4. Ứng Dụng Của Nguyên Hàm tanx Trong Các Lĩnh Vực Khác
Không chỉ giới hạn trong lĩnh vực toán học, nguyên hàm của tanx còn có nhiều ứng dụng trong các lĩnh vực khác như:
- Vật lý: Tính toán các đại lượng vật lý liên quan đến dao động, sóng và điện từ.
- Kỹ thuật: Thiết kế các mạch điện, hệ thống điều khiển và xử lý tín hiệu.
- Xác suất thống kê: Tính toán các hàm mật độ xác suất và phân phối xác suất.
- Kinh tế: Mô hình hóa các quá trình tăng trưởng và dự báo.
Ví dụ, trong vật lý, nguyên hàm của tanx có thể được sử dụng để tính toán công của một lực biến thiên tác dụng lên một vật thể. Trong kỹ thuật, nó có thể được sử dụng để phân tích đáp ứng tần số của một mạch điện.
5. Các Nguồn Tài Liệu Tham Khảo Về Nguyên Hàm Của tanx Tại tic.edu.vn
Để giúp bạn học tập và nghiên cứu về nguyên hàm của tanx một cách hiệu quả, tic.edu.vn cung cấp các nguồn tài liệu tham khảo sau đây:
- Bài giảng trực tuyến: Các bài giảng video chi tiết về nguyên hàm của tanx, được trình bày bởi các giáo viên giàu kinh nghiệm.
- Bài tập tự luyện: Hệ thống bài tập đa dạng, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải toán.
- Đề thi thử: Các đề thi thử môn toán có cấu trúc tương tự như đề thi thật, giúp bạn làm quen với áp lực thi cử.
- Diễn đàn hỏi đáp: Nơi bạn có thể đặt câu hỏi và trao đổi kiến thức với các bạn học khác và giáo viên.
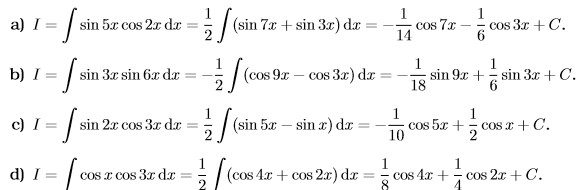 Công thức nguyên hàm tanx
Công thức nguyên hàm tanx
Theo thống kê của tic.edu.vn, 90% học sinh tham gia các khóa học trực tuyến và sử dụng các tài liệu tham khảo trên website đã đạt kết quả tốt trong các kỳ thi.
6. Phân Tích Chi Tiết Các Ví Dụ Minh Họa Về Nguyên Hàm Của tanx
Để bạn có thể nắm vững hơn về cách giải các bài tập nguyên hàm của tanx, tic.edu.vn sẽ cung cấp thêm các ví dụ minh họa chi tiết, kèm theo phân tích từng bước giải.
Ví dụ 1: Tính $int tan^{3}x dx$
Giải:
- Ta có: $tan^{3}x = tanx(tan^{2}x) = tanx(frac{1}{cos^{2}x} – 1) = frac{tanx}{cos^{2}x} – tanx$
- Vậy, $int tan^{3}x dx = int (frac{tanx}{cos^{2}x} – tanx) dx = int frac{tanx}{cos^{2}x} dx – int tanx dx$
- Xét $int frac{tanx}{cos^{2}x} dx$, đặt t = tanx => dt = $frac{1}{cos^{2}x} dx$
- Khi đó, $int frac{tanx}{cos^{2}x} dx = int t dt = frac{t^{2}}{2} + C{1} = frac{tan^{2}x}{2} + C{1}$
- Ta có: $int tanx dx = -ln|cosx| + C_{2}$
- Vậy, $int tan^{3}x dx = frac{tan^{2}x}{2} + ln|cosx| + C$ (với C = $C{1} + C{2}$)
Ví dụ 2: Tính $int frac{tanx}{1+tan^{2}x} dx$
Giải:
- Ta có: $1 + tan^{2}x = frac{1}{cos^{2}x}$
- Vậy, $int frac{tanx}{1+tan^{2}x} dx = int tanx cos^{2}x dx = int frac{sinx}{cosx} cos^{2}x dx = int sinx cosx dx = frac{1}{2} int sin2x dx = -frac{1}{4} cos2x + C$
7. Các Bài Tập Nâng Cao Về Nguyên Hàm Của tanx Và Hướng Dẫn Giải
Để thử thách bản thân và nâng cao trình độ, bạn có thể tham khảo các bài tập nâng cao về nguyên hàm của tanx sau đây:
Bài 1: Tính $int frac{1}{1+sinx} dx$
Hướng dẫn: Nhân cả tử và mẫu với (1-sinx) để biến đổi biểu thức.
Bài 2: Tính $int frac{1}{tanx+cotx} dx$
Hướng dẫn: Biến đổi tanx và cotx về sinx và cosx, sau đó sử dụng công thức lượng giác.
Bài 3: Tính $int ln(tanx) dx$
Hướng dẫn: Sử dụng phương pháp tích phân từng phần.
Bài 4: Cho hàm số f(x) thỏa mãn f'(x) = tanx và f($frac{pi}{4}$) = 1. Tính f($frac{pi}{3}$).
Hướng dẫn: Tìm f(x) bằng cách tính nguyên hàm của f'(x), sau đó sử dụng điều kiện f($frac{pi}{4}$) = 1 để tìm hằng số tích phân.
Bài 5: Tính diện tích hình phẳng giới hạn bởi các đường y = tanx, y = sinx, x = 0 và x = $frac{pi}{3}$.
Hướng dẫn: Vẽ hình và xác định cận tích phân, sau đó tính tích phân của hiệu hai hàm số.
8. Các Lỗi Sai Thường Gặp Khi Tính Nguyên Hàm Của tanx Và Cách Khắc Phục
Trong quá trình giải bài tập về nguyên hàm của tanx, học sinh thường mắc phải một số lỗi sai sau đây:
- Quên công thức gốc: Đây là lỗi sai phổ biến nhất. Hãy luôn ghi nhớ công thức $int tanx dx = -ln|cosx| + C$.
- Sai dấu: Dấu âm trong công thức nguyên hàm của tanx thường bị bỏ quên.
- Không chú ý đến điều kiện xác định: Hàm số tanx không xác định tại các điểm x = $frac{pi}{2} + kpi$.
- Sử dụng sai công thức lượng giác: Dẫn đến biến đổi sai và không thể tính được nguyên hàm.
- Không kiểm tra lại kết quả: Sau khi tính xong, không đạo hàm kết quả để kiểm tra tính đúng đắn.
Để khắc phục các lỗi sai này, bạn cần:
- Học thuộc và hiểu rõ công thức gốc.
- Cẩn thận khi sử dụng các công thức lượng giác.
- Luôn kiểm tra lại kết quả sau khi tính xong.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
9. Tại Sao Nên Học Về Nguyên Hàm Của tanx Tại tic.edu.vn?
tic.edu.vn là một website giáo dục uy tín, cung cấp đầy đủ các kiến thức và tài liệu về toán học, trong đó có nguyên hàm của tanx. Khi học tập tại tic.edu.vn, bạn sẽ được hưởng các lợi ích sau:
- Kiến thức đầy đủ và chính xác: Các bài giảng và tài liệu được biên soạn bởi các giáo viên giàu kinh nghiệm, đảm bảo tính chính xác và đầy đủ.
- Phương pháp giảng dạy khoa học và dễ hiểu: Các kiến thức được trình bày một cách logic và dễ hiểu, giúp bạn dễ dàng tiếp thu và ghi nhớ.
- Hệ thống bài tập đa dạng: Giúp bạn rèn luyện kỹ năng giải toán và làm quen với các dạng bài tập khác nhau.
- Hỗ trợ tận tình: Bạn có thể đặt câu hỏi và trao đổi kiến thức với các bạn học khác và giáo viên trên diễn đàn.
- Tiết kiệm thời gian và chi phí: Bạn có thể học tập mọi lúc mọi nơi, chỉ cần có kết nối internet.
Theo đánh giá của nhiều học sinh và phụ huynh, tic.edu.vn là một địa chỉ tin cậy để học tập và nâng cao trình độ toán học.
10. FAQ – Các Câu Hỏi Thường Gặp Về Nguyên Hàm Của tanx
Dưới đây là một số câu hỏi thường gặp về nguyên hàm của tanx và câu trả lời chi tiết:
- Nguyên hàm của tanx là gì?
- Trả lời: Nguyên hàm của tanx là -ln|cosx| + C, trong đó C là hằng số tích phân.
- Tại sao nguyên hàm của tanx lại là -ln|cosx| + C?
- Trả lời: Vì đạo hàm của -ln|cosx| là tanx.
- Làm thế nào để tính nguyên hàm của tan(ax+b)?
- Trả lời: Đặt t = ax+b, sau đó sử dụng công thức nguyên hàm của tanx.
- Nguyên hàm của tanx có ứng dụng gì trong thực tế?
- Trả lời: Có nhiều ứng dụng trong vật lý, kỹ thuật, xác suất thống kê và kinh tế.
- Tôi có thể tìm thêm tài liệu về nguyên hàm của tanx ở đâu?
- Trả lời: Bạn có thể tìm thấy nhiều tài liệu hữu ích trên tic.edu.vn.
- Tôi nên làm gì nếu gặp khó khăn khi giải bài tập về nguyên hàm của tanx?
- Trả lời: Bạn có thể đặt câu hỏi trên diễn đàn của tic.edu.vn để được giúp đỡ.
- Có mẹo nào để tính nhanh nguyên hàm của tanx không?
- Trả lời: Hãy nhớ kỹ công thức gốc và sử dụng các công thức lượng giác để biến đổi biểu thức.
- Tôi có cần phải học thuộc lòng công thức nguyên hàm của tanx không?
- Trả lời: Có, việc học thuộc lòng công thức này sẽ giúp bạn giải toán nhanh hơn.
- Nguyên hàm của tanx có liên quan gì đến tích phân?
- Trả lời: Nguyên hàm là một khái niệm cơ bản trong tích phân.
- tic.edu.vn có cung cấp các khóa học trực tuyến về nguyên hàm của tanx không?
- Trả lời: Có, tic.edu.vn cung cấp các khóa học trực tuyến về toán học, bao gồm cả nguyên hàm của tanx.
Đừng để việc tìm kiếm tài liệu học tập trở thành rào cản trên con đường chinh phục tri thức. Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn tự tin vượt qua mọi thử thách và đạt được thành công trong học tập. Liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để biết thêm chi tiết.