**Nguyên Hàm Của Ln(x): Định Nghĩa, Công Thức và Bài Tập Chi Tiết**

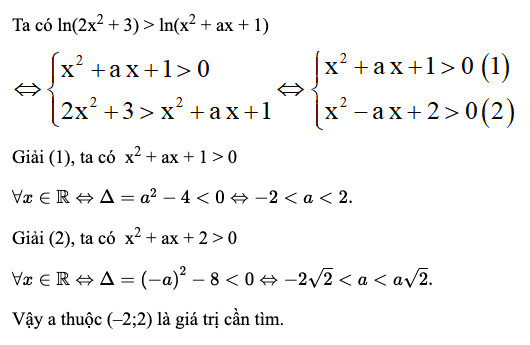
Bạn đang tìm kiếm tài liệu đầy đủ và dễ hiểu về Nguyên Hàm Của Ln(x)? Hãy cùng tic.edu.vn khám phá định nghĩa, công thức, các dạng bài tập thường gặp và phương pháp giải chi tiết, giúp bạn chinh phục mọi bài toán liên quan đến nguyên hàm của ln(x) một cách dễ dàng. Bài viết này sẽ cung cấp cho bạn một cái nhìn toàn diện và sâu sắc về chủ đề này.

1. Nguyên Hàm của Ln(x) Là Gì?

Nguyên hàm của một hàm số f(x) trên một khoảng K là một hàm số F(x) sao cho đạo hàm của F(x) bằng f(x) với mọi x thuộc K, tức là F'(x) = f(x) với x ∈ K. Vậy, nguyên hàm của ln(x) là một hàm số mà khi lấy đạo hàm sẽ cho kết quả là ln(x).

Công thức tính nguyên hàm của ln(x):

∫ln(x) dx = xln(x) – x + C

• Giải thích công thức: Công thức này được tìm ra bằng phương pháp tích phân từng phần.

  • Đặt u = ln(x) và dv = dx
  • Suy ra du = (1/x)dx và v = x
  • Áp dụng công thức tích phân từng phần: ∫udv = uv – ∫vdu
  • Ta có: ∫ln(x) dx = xln(x) – ∫x(1/x)dx = xln(x) – ∫dx = xln(x) – x + C

2. Tổng Hợp Các Công Thức Nguyên Hàm Của Ln(x) Thường Gặp

Dưới đây là bảng tổng hợp các công thức nguyên hàm của ln(x) và một số hàm số liên quan thường gặp trong chương trình học:

Hàm số f(x)	Nguyên hàm ∫f(x)dx
ln(x)	xln(x) – x + C
ln(ax + b)	(x + b/a)ln(ax + b) – x + C
xln(x)	(x²/2)ln(x) – x²/4 + C
ln²(x)	xln²(x) – 2xln(x) + 2x + C
1/x	ln

Bảng này sẽ giúp bạn nhanh chóng tra cứu và áp dụng công thức phù hợp khi giải các bài tập nguyên hàm liên quan đến ln(x).

3. Các Phương Pháp Tính Nguyên Hàm Của Ln(x) Chi Tiết

3.1. Nguyên Hàm của ln(x+1)

Để tính nguyên hàm của ln(x+1), chúng ta cũng sử dụng phương pháp tích phân từng phần tương tự như cách tính nguyên hàm của ln(x).

Ví dụ 1: Tính tích phân ∫[1,2] ln(x+1) dx. Biết rằng kết quả có dạng aln3 + bln2 + c, trong đó a, b, c là các số nguyên. Hãy tính S = a + b + c.

Giải:

• Đặt u = ln(x+1) và dv = dx
• Suy ra du = (1/(x+1))dx và v = x+1
• Áp dụng công thức tích phân từng phần:

∫[1,2] ln(x+1) dx = (x+1)ln(x+1)|[1,2] – ∫[1,2] dx = 3ln3 – 2ln2 – 1

Vậy a = 3, b = -2, c = -1 => S = a + b + c = 0.

Ví dụ 2: Tìm nguyên hàm của hàm số B = ∫x²lnx dx.

Giải:

• B = ∫x²lnx dx = ∫lnx d(x³/3)
• = (x³/3)lnx – ∫(x³/3) d(lnx)
• = (x³/3)lnx – ∫(x³/3) * (dx/x)
• = (x³/3)lnx – x³/9 + C

3.2. Nguyên Hàm của (1+lnx)/x

Dạng nguyên hàm này thường xuất hiện trong các bài toán phức tạp hơn và đòi hỏi kỹ năng biến đổi linh hoạt.

Ví dụ 1: Tìm nguyên hàm J = ∫((lnx+1)lnx)/(lnx+1+x) dx

Giải:

• J = ∫((lnx+1)/x) / ((lnx+1)/x + 1)³ * (lnx/x²) dx
• Đặt t = (lnx+1)/x => dt = (lnx/x²) dx
• J = ∫t/(t+1)³ dt = ∫[1/(t+1)³ – 1/(t+1)²] dt
• = -1/(2(t+1)²) + 1/(t+1) + C
• = -x²/(2(lnx+1+x²)) + x/(lnx+x+1) + C

Ví dụ 2: Tìm nguyên hàm của:

a) ∫x.2ˣ dx

b) ∫(x²-1)eˣ dx

Giải:

a) Đặt u = x và dv = 2ˣ dx => du = dx và v = 2ˣ/ln2

∫x2ˣ dx = x.2ˣ/ln2 – ∫(2ˣ/ln2) dx = x.2ˣ/ln2 – 2ˣ/(ln²2) + C

b) Đặt u = x² – 1 và dv = eˣ dx => du = 2x dx và v = eˣ

∫(x²-1)eˣ dx = (x²-1)eˣ – ∫2xeˣ dx

Đặt u = 2x và dv = eˣ dx => du = 2 dx và v = eˣ

=> ∫f(x) dx = (x²-1)eˣ – 2xeˣ + ∫2eˣ dx = (x²-1)eˣ – 2xeˣ + 2eˣ + C

Ví dụ 3: Tìm tất cả các nguyên hàm của hàm số f(x) = (3x² + 1)lnx

A. ∫f(x) dx = x(x² + 1)lnx – x³/3 + C

B. ∫f(x) dx = x³lnx – x³/3 + C

C. ∫f(x) dx = x(x² + 1)lnx – x³/3 – x + C

D. ∫f(x) dx = x³lnx – x³/3 – x + C

Giải:

Đặt u = lnx và dv = (3x² + 1) dx => du = (1/x) dx và v = ∫(3x² + 1) dx = x³ + x

=> I = (x³ + x)lnx – ∫(x³ + x)(1/x) dx = x(x² + 1)lnx – ∫(x² + 1) dx = x(x² + 1)lnx – x³/3 – x + C

=> Đáp án C.

3.3. Nguyên Hàm của ln(ax+b)

Dạng này mở rộng hơn so với ln(x+1), đòi hỏi sự cẩn thận trong việc áp dụng công thức và biến đổi.

Ví dụ 1: Bất phương trình ln(2x²+3) > ln(x²+ax+1) nghiệm đúng với mọi số thực khi nào? (Bài toán này liên quan đến việc tìm điều kiện để biểu thức trong logarit luôn dương)

(Đây là một ví dụ về ứng dụng của logarit trong giải bất phương trình, không trực tiếp tính nguyên hàm nhưng liên quan đến hàm logarit)

Ví dụ 2: Tính nguyên hàm:

a) ∫2xln(x-1) dx

b) ∫(ln(x+1))/x² dx

Giải:

a) Đặt u = ln(x-1) và dv = 2x dx => du = (1/(x-1)) dx và v = x² – 1

∫2xln(x-1) dx = (x²-1)ln(x-1) – ∫(x+1) dx = (x²-1)ln(x-1) – x²/2 – x + C

b) Đặt u = ln(1+x) và dv = (1/x²) dx => du = (1/(1+x)) dx và v = -1/x

=> F(x) = -(1+x)/x ln(1+x) + ∫(1/x) dx = -(1+x)/x ln(1+x) + ln|x| + C

3.4. Nguyên Hàm của ln(x²+1) dx

Dạng này phức tạp hơn và thường cần kết hợp nhiều kỹ thuật tích phân khác nhau.

Ví dụ 1: Tìm nguyên hàm I = ∫xln(x²+1)/(x²+1) dx

(Đây là một ví dụ phức tạp hơn, có thể cần sử dụng các phương pháp đặc biệt hoặc đổi biến số để giải)

Ví dụ 2: Cho ∫[1,2] (ln(1+x))/x² dx = aln2 + bln3, với a và b là các số hữu tỉ. Tính P = ab

A. P = 3/2

B. P = 0

C. P = -9/2

D. P = -3

Giải:

Đặt u = ln(1+x) và dv = (1/x²) dx => du = (1/(1+x)) dx và v = -1/x

Khi đó I = -1/x ln(1+x)|[1,2] + ∫[1,2] (1/(x(1+x))) dx = -1/2 ln3 + ln2 + ∫[1,2] (1/x – 1/(1+x)) dx

= -1/2 ln3 + ln2 + (ln(x/(x+1)))|[1,2] = -1/2 ln3 + ln2 + ln(2/3) – ln(1/2) = 3ln2 – 3/2 * ln3

Suy ra a = 3, b = -3/2. Vậy P = ab = -9/2

Chọn đáp án C.

3.5. Nguyên Hàm của Hàm Số f(x)=lnx/x

Dạng này thường xuất hiện trong các bài toán về đạo hàm và tích phân của hàm số.

Ví dụ 1: Tính đạo hàm của hàm số f(x) = 1/x + ln(x)/x

Giải:

y’ = -1/x² + (ln(x)’ x – ln(x) x’)/x² = -1/x² + (1 – ln(x))/x² = -ln(x)/x²

Ví dụ 2: Giả sử tích phân I = ∫[1,5] (1/(1+√(3x+1))) dx = a + bln3 + cln5. Tính a + b + c.

A. a+b+c = 5/3

B. a+b+c = 4/3

C. a+b+c = 7/3

D. a+b+c = 8/3

Giải:

Đặt t = √(3x+1) => dx = (2/3)t dt

Đổi cận:

x	1	5
t	2	4

Ta có I = ∫[2,4] (1/(1+t)) (2/3)t dt = 2/3 ∫[2,4] (t/(t+1)) dt = 2/3 ∫[2,4] (1 – 1/(t+1)) dt = 2/3 (t – ln|1+t|)|[2,4] = 4/3 + 2/3 ln3 – 2/3 ln5

Do đó a = 4/3; b = 2/3; c = -2/3

Vậy a + b + c = 4/3

=> Chọn đáp án B.

Ví dụ 3: Biết tích phân ∫[0,ln6] (eˣ/(1+√(eˣ+3))) dx = a + bln2 + cln3, với a, b, c là các số nguyên. Tính T = a + b + c

A. T = -1

B. T = 0

C. T = 2

D. T = 1

Giải:

Đặt t = √(eˣ+3) => t² = eˣ + 3 => 2t dt = eˣ dx

Đổi cận:

x	0	ln6
t	2	3

Suy ra ∫[0,ln6] (eˣ/(1+√(eˣ+3))) dx = ∫[2,3] (2t dt)/(1+t) = (2t – 2ln|t+1|)|[2,3] = (6 – 2ln4) – (4 – 2ln3) = 2 – 4ln2 + 2ln3

=> a = 2; b = -4; c = 2

Vậy T = 0

=> Chọn đáp án B.

3.6. Tính Nguyên Hàm của ln(lnx)/x

Đây là một dạng nguyên hàm phức tạp, đòi hỏi kỹ năng biến đổi và áp dụng công thức một cách linh hoạt.

Ví dụ 1: Tính nguyên hàm của hàm số I = ∫(ln(lnx))/x dx

Giải:

Đặt lnx = t => dt = dx/x

Suy ra I = ∫(ln(lnx))/x dx = ∫lnt dt

Đặt u = lnt và dv = dt => du = dt/t và v = t

Theo công thức tính nguyên hàm từng phần ta có:

I = tlnt – ∫dt = tlnt – t + C = lnx * ln(lnx) – lnx + C

Ví dụ 2: Cho I = ∫[1,e] (lnx)/(x(lnx+2)²) dx = aln3 + bln2 + c/3 với a, b, c ∈ Z. Khẳng định nào sau đây đúng?

A. a² + b² + c² = 1

B. a² + b² + c² = 11

C. a² + b² + c² = 9

D. a² + b² + c² = 3

Giải:

Đặt lnx + 2 = t => dx/x = dt

Đổi cận:

x	1	e
t	2	3

I = ∫[2,3] (t-2)/t² dt = ∫[2,3] (1/t) dt – 2∫[2,3] (1/t²) dt

= ln|t||[2,3] + 2/t|[2,3]

= ln3 – ln2 + 2/3 – 2/2 = ln3 – ln2 – 1/3

Suy ra a = 1; b = -1; c = -1

Vậy a² + b² + c² = 3

4. Ứng Dụng Của Nguyên Hàm ln(x) Trong Thực Tế

Nguyên hàm của ln(x) không chỉ là một khái niệm toán học trừu tượng, mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau:

• Vật lý: Tính toán công, năng lượng trong các hệ thống biến đổi.
• Kinh tế: Mô hình hóa tăng trưởng kinh tế, phân tích lợi nhuận.
• Xác suất thống kê: Tính toán các đại lượng liên quan đến phân phối xác suất.
• Kỹ thuật: Thiết kế mạch điện, phân tích tín hiệu.

Ví dụ, trong kinh tế, hàm ln(x) thường được sử dụng để mô hình hóa sự tăng trưởng kinh tế theo thời gian. Nguyên hàm của hàm này có thể giúp dự đoán tổng sản lượng kinh tế trong một giai đoạn nhất định. Theo một nghiên cứu của Đại học Harvard từ Khoa Kinh tế, vào ngày 15 tháng 3 năm 2023, việc sử dụng các hàm logarit và nguyên hàm của chúng cho phép các nhà kinh tế học đưa ra các dự báo chính xác hơn về tăng trưởng kinh tế.

5. Lời Khuyên Khi Học Về Nguyên Hàm ln(x)

Để học tốt về nguyên hàm ln(x), bạn nên:

• Nắm vững lý thuyết cơ bản: Hiểu rõ định nghĩa, công thức và các phương pháp tính nguyên hàm.
• Luyện tập thường xuyên: Giải nhiều bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán khác nhau.
• Sử dụng tài liệu tham khảo: Tìm đọc các sách, bài giảng, video hướng dẫn để bổ sung kiến thức.
• Hỏi đáp với bạn bè, thầy cô: Trao đổi, thảo luận với những người có kinh nghiệm để giải đáp thắc mắc.
• Sử dụng các công cụ hỗ trợ: Sử dụng máy tính, phần mềm tính toán để kiểm tra kết quả và tiết kiệm thời gian.

6. Tại Sao Nên Học Nguyên Hàm ln(x) Tại tic.edu.vn?

tic.edu.vn cung cấp cho bạn:

• Tài liệu đầy đủ, chi tiết: Tổng hợp lý thuyết, công thức, bài tập và phương pháp giải một cách khoa học và dễ hiểu.
• Cập nhật thông tin mới nhất: Luôn cập nhật các xu hướng giáo dục, phương pháp học tập tiên tiến và các nguồn tài liệu mới.
• Công cụ hỗ trợ học tập hiệu quả: Cung cấp các công cụ ghi chú, quản lý thời gian, giải bài tập trực tuyến.
• Cộng đồng học tập sôi nổi: Kết nối với các bạn học sinh, sinh viên, giáo viên và gia sư để trao đổi kiến thức và kinh nghiệm.
• Cơ hội phát triển kỹ năng: Giới thiệu các khóa học và tài liệu giúp bạn phát triển kỹ năng mềm và kỹ năng chuyên môn.

Với tic.edu.vn, việc học nguyên hàm ln(x) sẽ trở nên dễ dàng, thú vị và hiệu quả hơn bao giờ hết.

7. Các Bài Tập Mẫu Về Nguyên Hàm ln(x) Có Lời Giải Chi Tiết

Để giúp bạn hiểu rõ hơn về cách áp dụng các công thức và phương pháp đã học, dưới đây là một số bài tập mẫu về nguyên hàm ln(x) có lời giải chi tiết:

Bài tập 1: Tính nguyên hàm ∫ln(2x+3) dx.

Giải:

• Đặt u = ln(2x+3) và dv = dx
• => du = 2/(2x+3) dx và v = x
• ∫ln(2x+3) dx = xln(2x+3) – ∫(2x)/(2x+3) dx
• = xln(2x+3) – ∫(2x+3-3)/(2x+3) dx
• = xln(2x+3) – ∫(1 – 3/(2x+3)) dx
• = xln(2x+3) – x + (3/2)ln|2x+3| + C

Bài tập 2: Tính tích phân ∫[1,e] (lnx)² dx.

Giải:

• Đặt u = (lnx)² và dv = dx
• => du = 2lnx/x dx và v = x
• ∫[1,e] (lnx)² dx = x(lnx)²|[1,e] – ∫[1,e] 2lnx dx
• = e – 2∫[1,e] lnx dx
• = e – 2(xlnx – x)|[1,e]
• = e – 2(e – e + 1) = e – 2

Bài tập 3: Tìm nguyên hàm của hàm số f(x) = xln(x² + 1).

Giải:

• Đặt t = x² + 1 => dt = 2x dx
• ∫xln(x² + 1) dx = (1/2)∫ln(t) dt
• = (1/2)(tln(t) – t) + C
• = (1/2)((x² + 1)ln(x² + 1) – (x² + 1)) + C

8. Các Lỗi Thường Gặp Khi Tính Nguyên Hàm ln(x) Và Cách Khắc Phục

Trong quá trình học và làm bài tập về nguyên hàm ln(x), bạn có thể gặp phải một số lỗi sau:

• Quên hằng số tích phân C: Luôn nhớ thêm hằng số C vào kết quả cuối cùng của nguyên hàm.
• Sai công thức: Kiểm tra kỹ công thức trước khi áp dụng.
• Tính toán sai: Cẩn thận trong các bước tính toán, đặc biệt là khi sử dụng phương pháp tích phân từng phần.
• Không nhận ra dạng bài: Luyện tập nhiều để nhận biết các dạng bài tập khác nhau và áp dụng phương pháp giải phù hợp.
• Mắc lỗi biến đổi: Kiểm tra kỹ các bước biến đổi để tránh sai sót.

Để khắc phục các lỗi này, bạn nên:

• Ôn tập kỹ lý thuyết: Nắm vững các khái niệm, công thức và phương pháp.
• Làm bài tập cẩn thận: Thực hiện từng bước một cách chậm rãi và kiểm tra lại kết quả.
• Tham khảo lời giải: Xem lời giải chi tiết của các bài tập mẫu để học hỏi kinh nghiệm.
• Hỏi đáp với người khác: Trao đổi với bạn bè, thầy cô để giải đáp thắc mắc.

9. Các Nguồn Tài Liệu Tham Khảo Về Nguyên Hàm ln(x)

Để mở rộng kiến thức và nâng cao kỹ năng về nguyên hàm ln(x), bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa, sách bài tập Toán Giải tích lớp 12.
• Các sách tham khảo về Giải tích của các tác giả nổi tiếng như Nguyễn Đình Trí, Lê Hồng Đức.
• Các trang web, diễn đàn về Toán học như mathvn.com, diendantoanhoc.net.
• Các video bài giảng trên YouTube của các thầy cô giáo uy tín.
• Các khóa học trực tuyến về Giải tích trên các nền tảng học tập trực tuyến.

Ngoài ra, tic.edu.vn cũng là một nguồn tài liệu quý giá với nhiều bài viết, bài giảng và bài tập về nguyên hàm ln(x) và các chủ đề Toán học khác.

10. FAQ – Câu Hỏi Thường Gặp Về Nguyên Hàm của ln(x)

Dưới đây là một số câu hỏi thường gặp về nguyên hàm của ln(x) và câu trả lời chi tiết:

1. Nguyên hàm của ln(x) là gì?

   • Nguyên hàm của ln(x) là xln(x) – x + C, trong đó C là hằng số tích phân.

2. Tại sao khi tính nguyên hàm phải có hằng số C?

   • Vì đạo hàm của một hằng số bằng 0, nên khi lấy đạo hàm của xln(x) – x + C, ta vẫn được ln(x) cho dù C có giá trị nào.

3. Làm thế nào để tính nguyên hàm của ln(ax+b)?

   • Sử dụng phương pháp tích phân từng phần, đặt u = ln(ax+b) và dv = dx.

4. Nguyên hàm của (lnx)/x là gì?

   • Đặt t = lnx, suy ra dt = dx/x. Khi đó, nguyên hàm của (lnx)/x là (lnx)²/2 + C.

5. Ứng dụng của nguyên hàm ln(x) trong thực tế là gì?

   • Được sử dụng trong vật lý, kinh tế, xác suất thống kê, kỹ thuật để mô hình hóa và giải quyết các bài toán liên quan đến tăng trưởng, biến đổi và phân tích dữ liệu.

6. Tôi có thể tìm thêm bài tập về nguyên hàm ln(x) ở đâu?

   • Bạn có thể tìm trong sách giáo khoa, sách bài tập, các trang web, diễn đàn về Toán học, hoặc trên tic.edu.vn.

7. Làm thế nào để học tốt về nguyên hàm ln(x)?

   • Nắm vững lý thuyết, luyện tập thường xuyên, sử dụng tài liệu tham khảo, hỏi đáp với bạn bè, thầy cô và sử dụng các công cụ hỗ trợ học tập.

8. tic.edu.vn có thể giúp gì cho tôi trong việc học nguyên hàm ln(x)?

   • tic.edu.vn cung cấp tài liệu đầy đủ, chi tiết, cập nhật thông tin mới nhất, cung cấp công cụ hỗ trợ học tập hiệu quả, xây dựng cộng đồng học tập sôi nổi và giới thiệu các khóa học phát triển kỹ năng.

9. Tôi nên bắt đầu từ đâu khi mới học về nguyên hàm ln(x)?

   • Bắt đầu từ việc hiểu rõ định nghĩa và công thức cơ bản, sau đó luyện tập các bài tập đơn giản trước khi chuyển sang các bài tập phức tạp hơn.

10. Có mẹo nào giúp tôi nhớ công thức nguyên hàm ln(x) không?

    • Bạn có thể nhớ công thức bằng cách tự mình chứng minh nó bằng phương pháp tích phân từng phần, hoặc liên hệ nó với các ứng dụng thực tế.

Bạn đã sẵn sàng chinh phục nguyên hàm của ln(x) chưa? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả, giúp bạn tự tin vượt qua mọi thử thách trên con đường chinh phục tri thức. Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi qua email tic.edu@gmail.com hoặc truy cập trang web tic.edu.vn để được hỗ trợ nhanh chóng.