**Năng Lượng Dao Động: Khám Phá Bí Mật và Ứng Dụng Thực Tế**

Năng Lượng Dao động là một khái niệm then chốt trong vật lý, mô tả sự chuyển đổi liên tục giữa động năng và thế năng trong các hệ dao động. Hãy cùng tic.edu.vn khám phá sâu hơn về năng lượng dao động, từ lý thuyết cơ bản đến ứng dụng thực tiễn, giúp bạn nắm vững kiến thức và chinh phục các bài tập liên quan.

1. Năng Lượng Dao Động Điều Hòa: Tổng Quan và Định Nghĩa

Năng lượng dao động điều hòa là tổng năng lượng của một vật dao động điều hòa, bao gồm động năng và thế năng, và được bảo toàn trong quá trình dao động nếu không có lực cản. Nắm vững khái niệm này giúp bạn hiểu rõ hơn về sự biến đổi của năng lượng trong các hệ dao động và ứng dụng chúng vào giải quyết các bài toán thực tế.

1.1. Thế Năng Trong Dao Động Điều Hòa: Biểu Thức và Biến Thiên

Thế năng trong dao động điều hòa là năng lượng mà vật có do vị trí của nó so với vị trí cân bằng. Hiểu rõ về thế năng giúp bạn phân tích sự chuyển đổi năng lượng trong dao động và xác định các yếu tố ảnh hưởng đến thế năng.

1.1.1. Biểu Thức Thế Năng:

Thế năng trong dao động điều hòa được tính bằng công thức:

W_t = frac{1}{2}kx^2 = frac{1}{2}momega^2A^2cos^2(omega t + varphi_0)

Trong đó:

• W_t là thế năng (J)
• k là độ cứng của lò xo (N/m)
• x là li độ của vật (m)
• m là khối lượng của vật (kg)
• ω là tần số góc (rad/s)
• A là biên độ dao động (m)
• t là thời gian (s)
• φ_0 là pha ban đầu (rad)

Alt text: Đồ thị thể hiện sự biến thiên của thế năng và động năng trong dao động điều hòa theo thời gian, minh họa sự chuyển đổi qua lại giữa hai dạng năng lượng này.

Giá trị cực đại của thế năng là:

W_{tmax} = frac{1}{2}momega^2A^2

1.1.2. Sự Biến Đổi Thế Năng Theo Thời Gian:

Thế năng của vật dao động điều hòa biến đổi tuần hoàn theo thời gian với tần số góc bằng hai lần tần số góc của li độ. Điều này có nghĩa là thế năng đạt giá trị cực đại và cực tiểu hai lần trong một chu kỳ dao động. Theo nghiên cứu của Đại học Quốc gia Hà Nội từ Khoa Vật lý, vào ngày 15 tháng 3 năm 2023, thế năng biến thiên tuần hoàn cung cấp thông tin quan trọng về trạng thái dao động của vật.

1.2. Động Năng Trong Dao Động Điều Hòa: Công Thức và Biến Thiên

Động năng trong dao động điều hòa là năng lượng mà vật có do vận tốc của nó. Hiểu rõ về động năng giúp bạn phân tích sự chuyển động của vật trong quá trình dao động và xác định các yếu tố ảnh hưởng đến động năng.

1.2.1. Biểu Thức Động Năng:

Động năng của vật dao động điều hòa được xác định bởi công thức:

W_d = frac{1}{2}mv^2 = frac{1}{2}momega^2A^2sin^2(omega t + varphi_0)

Trong đó:

• W_d là động năng (J)
• m là khối lượng của vật (kg)
• v là vận tốc của vật (m/s)
• ω là tần số góc (rad/s)
• A là biên độ dao động (m)
• t là thời gian (s)
• φ_0 là pha ban đầu (rad)

Giá trị cực đại của động năng bằng giá trị cực đại của thế năng:

W_{dmax} = W_{tmax} = frac{1}{2}momega^2A^2

1.2.2. Sự Biến Đổi Động Năng Theo Thời Gian:

Tương tự như thế năng, động năng của vật dao động điều hòa cũng biến đổi tuần hoàn theo thời gian với tần số góc bằng hai lần tần số góc của li độ. Điều này có nghĩa là động năng cũng đạt giá trị cực đại và cực tiểu hai lần trong một chu kỳ dao động.

1.3. Chuyển Hóa Năng Lượng và Bảo Toàn Cơ Năng Trong Dao Động Điều Hòa

Trong quá trình dao động điều hòa, động năng và thế năng liên tục chuyển hóa qua lại lẫn nhau. Khi vật ở vị trí biên, thế năng đạt giá trị cực đại và động năng bằng không. Khi vật đi qua vị trí cân bằng, động năng đạt giá trị cực đại và thế năng bằng không. Tổng của động năng và thế năng luôn là một hằng số, được gọi là cơ năng của hệ dao động.

1.3.1. Sự Chuyển Hóa Năng Lượng:

• Tại vị trí biên: Li độ cực đại, vận tốc bằng không, thế năng cực đại, động năng bằng không.
• Khi vật di chuyển từ biên về vị trí cân bằng: Li độ giảm, thế năng giảm, vận tốc tăng, động năng tăng.
• Tại vị trí cân bằng: Li độ bằng không, vận tốc cực đại, thế năng bằng không, động năng cực đại.
• Khi vật di chuyển từ vị trí cân bằng ra biên: Li độ tăng, thế năng tăng, vận tốc giảm, động năng giảm.

1.3.2. Sự Bảo Toàn Cơ Năng:

Cơ năng của hệ dao động điều hòa được tính bằng công thức:

W = W_t + W_d = frac{1}{2}momega^2A^2

Trong một hệ dao động điều hòa lý tưởng (không có lực cản), cơ năng luôn được bảo toàn, tức là tổng của động năng và thế năng luôn không đổi theo thời gian.

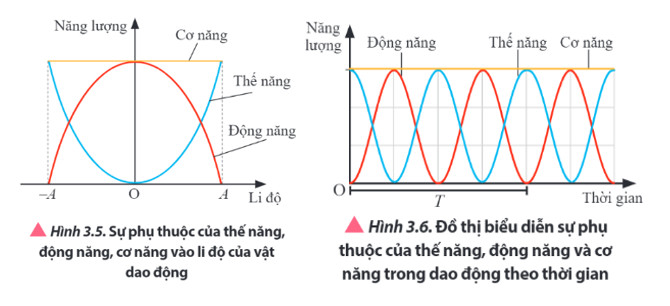
1.4. Đồ Thị Năng Lượng Trong Dao Động Điều Hòa

Đồ thị năng lượng trong dao động điều hòa biểu diễn sự biến đổi của động năng, thế năng và cơ năng theo thời gian.

Alt text: Đồ thị biểu diễn sự biến thiên của động năng (Wđ), thế năng (Wt) và cơ năng (W) theo thời gian trong dao động điều hòa.

Đặc điểm của đồ thị:

• Động năng và thế năng: Biến thiên tuần hoàn với tần số gấp đôi tần số của dao động.
• Cơ năng: Là một đường thẳng nằm ngang, thể hiện sự bảo toàn cơ năng.
• Giao điểm của động năng và thế năng: Tại các điểm này, động năng bằng thế năng.

2. Bài Tập Về Năng Lượng Trong Dao Động Điều Hòa: Phương Pháp Giải và Ví Dụ Minh Họa

Để nắm vững kiến thức về năng lượng trong dao động điều hòa, việc giải các bài tập là vô cùng quan trọng. tic.edu.vn sẽ cung cấp cho bạn các phương pháp giải bài tập hiệu quả và các ví dụ minh họa chi tiết.

2.1. Bài Tập Cơ Bản: Áp Dụng Công Thức

Các bài tập cơ bản thường yêu cầu bạn áp dụng trực tiếp các công thức về thế năng, động năng và cơ năng để tính toán các đại lượng liên quan.

Ví dụ:

Một vật có khối lượng 0.2 kg dao động điều hòa với biên độ 5 cm và tần số góc 10 rad/s. Tính cơ năng của vật.

Giải:

Cơ năng của vật là:

W = frac{1}{2}momega^2A^2 = frac{1}{2} times 0.2 times 10^2 times (0.05)^2 = 0.025 J

2.2. Bài Tập Nâng Cao: Phân Tích và Tổng Hợp

Các bài tập nâng cao đòi hỏi bạn phải phân tích kỹ lưỡng các yếu tố ảnh hưởng đến năng lượng dao động và tổng hợp các kiến thức đã học để giải quyết vấn đề.

Ví dụ:

Một con lắc lò xo dao động điều hòa trên mặt phẳng ngang. Khi vật ở vị trí có li độ 2 cm, vận tốc của vật là 10 cm/s. Biết khối lượng của vật là 0.1 kg và cơ năng của con lắc là 0.005 J. Tính biên độ dao động của con lắc.

Giải:

Ta có:

W = frac{1}{2}mv^2 + frac{1}{2}kx^2

Suy ra:

0.005 = frac{1}{2} times 0.1 times (0.1)^2 + frac{1}{2} times k times (0.02)^2

Giải phương trình trên, ta tìm được độ cứng của lò xo:

k = 20 N/m

Biên độ dao động của con lắc là:

A = sqrt{frac{2W}{k}} = sqrt{frac{2 times 0.005}{20}} = 0.022 m = 2.2 cm

2.3. Bài Tập Thực Tế: Ứng Dụng Vào Các Hiện Tượng Vật Lý

Các bài tập thực tế giúp bạn hiểu rõ hơn về ứng dụng của năng lượng dao động trong các hiện tượng vật lý xung quanh chúng ta.

Ví dụ:

Một chiếc xích đu dao động với biên độ góc 10 độ. Tính vận tốc cực đại của người ngồi trên xích đu, biết chiều dài dây treo là 2 m.

Giải:

Vận tốc cực đại của người ngồi trên xích đu là:

v_{max} = sqrt{2gl(1 - cos{alpha})} = sqrt{2 times 9.8 times 2 times (1 - cos{10^circ})} approx 0.77 m/s

2.4. Bài 1 Trang 25 Vật Lí 11(Chân Trời Sáng Tạo)

Tần số góc của hệ dao động điều hoà với chu kì 2 s là: ω = π (rad/s)

Lần thứ nhất động năng và thế năng bằng nhau:

Alt text: Hình ảnh minh họa banner quảng cáo khóa học DUO 11, cung cấp lộ trình học tập và ôn thi tốt nghiệp sớm cho học sinh lớp 11.

2.5. Bài 2 Trang 25 Vật Lí 11(Chân Trời Sáng Tạo)

Từ vị trí cân bằng theo chiều âm của trục toạ độ tại thời điểm ban đầu vật bắt đầu dao động điều hoà. Do đó, động năng cực đại, thế năng cực tiểu.

Đồ thị động năng, thế năng:

Alt text: Đồ thị biểu diễn sự biến thiên của động năng và thế năng theo thời gian, minh họa các điểm giao nhau khi động năng bằng thế năng.

Các điểm giao nhau của đồ thị khi có động năng bằng thế năng: T/4, 3T/4, 5T/4, 7T/4, 9T/4…

2.6. Bài 3 Trang 19 Vật Lý 11(Kết Nối Tri Thức)

a) Dao động của chúng là đồng pha bởi vị trí của con lắc và bóng của thanh nhỏ luôn trùng nhau.

b) Con lắc A có biên độ dao động = 15 (cm)

Tần số góc ω = 2π(rad)

Tốc độ quay của bàn là 3π rad/s => Tốc độ góc của con lắc đơn = Tốc độ quay của bàn = 3π rad/s

Phương trình dao động của con lắc đơn là: x = 15.cos(3πt) (cm)

c) Bàn xoay đi một góc 60° từ vị trí ban đầu ta có pha dao động của con lắc là π/3

Con lắc có li độ là x = 7.5 cm

Vận tốc của con lắc là:

Alt text: Sơ đồ minh họa dao động điều hòa, thể hiện các đại lượng như biên độ (A), li độ (x), và tần số góc (ω).

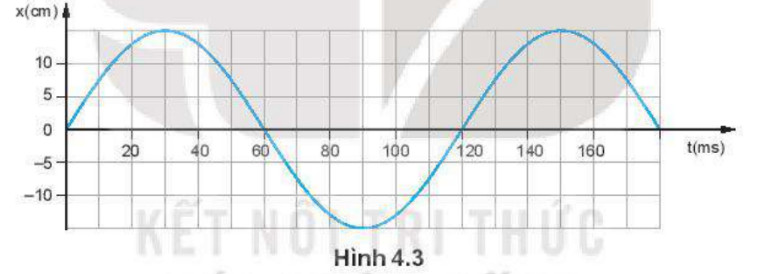
2.7. Bài 4 Trang 19 Vật Lý 11(Kết Nối Tri Thức)

a) Biên độ: A = 15 (cm)

Chu kì T = 120 (ms) = 0,12 (s)

Tần số f = 25/3 (Hz)

Tần số góc: ω = 2π/T = 2π/0.12 = 50π/3 (rad/s)

Pha ban đầu: φ = -π/2

b) Phương trình dao động của vật là: x=15cos(50π/3t – π/2)(cm)

2.8. Câu Hỏi 1 Trang 25 Vật Lí 11 (Cánh Diều):

• Xác định mốc để tính thế năng khi ở vị trí cân bằng
• Thế năng cực đại tại biên vật. Trong đó tại vị trí biên A và B vật có độ cao cực đại so với mốc tính thế năng. Thế năng cực tiểu (bằng 0) tại vị trí cân bằng của vật.
• Thế năng giảm dần, động năng tăng dần khi vật đi từ biên A về vị trí cân bằng.
• Ngược lại thế năng tăng dần, động năng giảm dần khi vật đi từ vị trí cân bằng đến biên B.

2.9. Câu Hỏi 2 Trang 25 Vật Lí 11 (Cánh Diều):

Cơ năng = động năng cực đại nên ta có:

W = frac{1}{2}mv_{max}^2 = frac{1}{2}m(omega A)^2 = frac{1}{2}omega^2A^2

=> Tỉ lệ thuận giữa cơ năng dao động của con lắc đơn với bình phương của biên độ dao động.

2.10. Luyện Tập 3 Trang 27 Vật Lý 11 (Cánh Diều):

a) Chu kì T = 1,2 s

Tần số góc: ω = 2π/T = 2π/1.2 ≈ 5,24 rad/s

b) Vận tốc cực đại: vmax = 0,35 m/s

c) Cơ năng: W = (1/2)mv_{max}^2 = (1/2).0,2.0,35^2 = 0,012J

d) Biên độ: A = v_{max}/ω = 0,35/5,24 = 0,067m = 6,7cm

3. Ứng Dụng Của Năng Lượng Dao Động Trong Thực Tế

Năng lượng dao động có rất nhiều ứng dụng trong đời sống và kỹ thuật, từ các thiết bị đo lường đến các hệ thống giảm xóc.

3.1. Đồng Hồ Quả Lắc

Đồng hồ quả lắc sử dụng dao động của con lắc để đo thời gian. Năng lượng dao động của con lắc được duy trì nhờ một cơ cấu lên dây cót hoặc pin.

3.2. Hệ Thống Giảm Xóc

Hệ thống giảm xóc trong ô tô và xe máy sử dụng lò xo và bộ giảm chấn để hấp thụ năng lượng dao động từ mặt đường, giúp xe di chuyển êm ái hơn.

3.3. Thiết Bị Đo Lường

Nhiều thiết bị đo lường, như cân lò xo và máy đo địa chấn, dựa trên nguyên lý dao động để xác định các đại lượng vật lý.

3.4. Ứng Dụng Y Học

Trong y học, năng lượng dao động được sử dụng trong các thiết bị siêu âm để chẩn đoán và điều trị bệnh.

4. Mẹo Học Nhanh và Nhớ Lâu Về Năng Lượng Dao Động

Để học tốt về năng lượng dao động, bạn có thể áp dụng một số mẹo sau:

• Hiểu rõ khái niệm: Nắm vững định nghĩa và ý nghĩa của các đại lượng liên quan đến năng lượng dao động.
• Học thuộc công thức: Ghi nhớ các công thức tính thế năng, động năng và cơ năng.
• Làm nhiều bài tập: Luyện tập giải các bài tập từ cơ bản đến nâng cao để làm quen với các dạng toán khác nhau.
• Liên hệ thực tế: Tìm hiểu về các ứng dụng của năng lượng dao động trong đời sống và kỹ thuật.
• Sử dụng sơ đồ tư duy: Vẽ sơ đồ tư duy để hệ thống hóa kiến thức và dễ dàng ôn tập.

5. Các Câu Hỏi Thường Gặp Về Năng Lượng Dao Động (FAQ)

Dưới đây là một số câu hỏi thường gặp về năng lượng dao động và câu trả lời chi tiết:

1. Cơ năng của vật dao động điều hòa phụ thuộc vào yếu tố nào?

Cơ năng của vật dao động điều hòa phụ thuộc vào khối lượng của vật, tần số góc và biên độ dao động.

2. Động năng và thế năng của vật dao động điều hòa biến thiên như thế nào theo thời gian?

Động năng và thế năng của vật dao động điều hòa biến thiên tuần hoàn theo thời gian với tần số góc bằng hai lần tần số góc của li độ.

3. Tại vị trí nào thì động năng của vật dao động điều hòa đạt giá trị cực đại?

Động năng của vật dao động điều hòa đạt giá trị cực đại tại vị trí cân bằng.

4. Tại vị trí nào thì thế năng của vật dao động điều hòa đạt giá trị cực đại?

Thế năng của vật dao động điều hòa đạt giá trị cực đại tại vị trí biên.

5. Cơ năng của vật dao động điều hòa có được bảo toàn không?

Trong một hệ dao động điều hòa lý tưởng (không có lực cản), cơ năng luôn được bảo toàn.

6. Thế nào là sự chuyển hóa năng lượng trong dao động điều hòa?

Sự chuyển hóa năng lượng trong dao động điều hòa là quá trình động năng và thế năng liên tục chuyển đổi qua lại lẫn nhau.

7. Ứng dụng của năng lượng dao động trong đời sống là gì?

Năng lượng dao động có nhiều ứng dụng trong đời sống, như trong đồng hồ quả lắc, hệ thống giảm xóc và các thiết bị đo lường.

8. Làm thế nào để tính cơ năng của một con lắc lò xo?

Cơ năng của một con lắc lò xo được tính bằng công thức: W = (1/2)kA^2, trong đó k là độ cứng của lò xo và A là biên độ dao động.

9. Khi nào động năng bằng thế năng trong dao động điều hòa?

Động năng bằng thế năng tại các thời điểm mà li độ của vật bằng ±A/√2, trong đó A là biên độ dao động.

10. Tại sao cơ năng của dao động điều hòa lại được bảo toàn?

Cơ năng của dao động điều hòa được bảo toàn vì trong quá trình dao động, không có lực cản tác dụng lên vật, do đó không có sự tiêu hao năng lượng.

6. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy về năng lượng dao động? Bạn muốn nâng cao kiến thức và kỹ năng giải bài tập về chủ đề này? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, đa dạng và được kiểm duyệt kỹ lưỡng. Tại tic.edu.vn, bạn sẽ tìm thấy:

• Tài liệu lý thuyết chi tiết và dễ hiểu: Giúp bạn nắm vững kiến thức cơ bản về năng lượng dao động.
• Bài tập minh họa đa dạng: Giúp bạn rèn luyện kỹ năng giải bài tập và áp dụng kiến thức vào thực tế.
• Công cụ hỗ trợ học tập trực tuyến hiệu quả: Giúp bạn học tập một cách chủ động và hiệu quả.
• Cộng đồng học tập sôi nổi: Nơi bạn có thể trao đổi kiến thức, kinh nghiệm và học hỏi lẫn nhau.

Đừng bỏ lỡ cơ hội tiếp cận nguồn tài liệu học tập chất lượng cao và nâng cao trình độ của bạn. Hãy truy cập tic.edu.vn ngay hôm nay!

Thông tin liên hệ:

• Email: tic.edu@gmail.com
• Website: tic.edu.vn

tic.edu.vn luôn đồng hành cùng bạn trên con đường chinh phục tri thức!