Muốn Tính Chu Vi: Bí Quyết Nắm Vững Công Thức Và Ứng Dụng

Bạn đang tìm kiếm cách tính chu vi hình vuông một cách dễ hiểu và ứng dụng thực tế? Bài viết này từ tic.edu.vn sẽ cung cấp cho bạn công thức, ví dụ minh họa và những lưu ý quan trọng để bạn nắm vững kiến thức này. Cùng khám phá bí quyết tính chu vi và làm chủ các bài toán liên quan đến hình vuông nhé!

1. Chu Vi Hình Vuông: Định Nghĩa Và Công Thức Vàng

1.1 Chu vi hình vuông là gì?

Chu vi hình vuông là tổng độ dài của tất cả các cạnh của hình vuông đó. Nói một cách đơn giản, nếu bạn đi bộ một vòng quanh hình vuông, quãng đường bạn đi chính là chu vi của nó.

1.2 Công thức tính chu vi hình vuông siêu dễ nhớ

Vì hình vuông có bốn cạnh bằng nhau, việc tính chu vi trở nên cực kỳ đơn giản. Công thức tính chu vi hình vuông như sau:

Chu vi = Độ dài một cạnh x 4

Hoặc:

C = a x 4

Trong đó:

• C là chu vi hình vuông
• a là độ dài một cạnh của hình vuông

Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15/03/2023, việc nắm vững công thức tính chu vi giúp học sinh dễ dàng giải quyết các bài toán liên quan đến hình học.

1.3 Ví dụ minh họa cách tính chu vi hình vuông

Ví dụ 1: Một hình vuông có cạnh dài 7cm. Tính chu vi của hình vuông đó.

Giải:

Áp dụng công thức: C = a x 4 = 7cm x 4 = 28cm

Vậy chu vi hình vuông là 28cm.

Ví dụ 2: Một mảnh vườn hình vuông có cạnh dài 12m. Người ta muốn làm hàng rào bao quanh mảnh vườn. Hỏi cần bao nhiêu mét hàng rào?

Giải:

Số mét hàng rào cần dùng chính là chu vi của mảnh vườn.

Áp dụng công thức: C = a x 4 = 12m x 4 = 48m

Vậy cần 48 mét hàng rào.

1.4 Các dạng bài tập thường gặp về chu vi hình vuông

• Dạng 1: Tính chu vi khi biết độ dài cạnh: Đây là dạng bài tập cơ bản, chỉ cần áp dụng công thức là có thể giải được.
• Dạng 2: Tính độ dài cạnh khi biết chu vi: Để giải dạng bài này, bạn cần chia chu vi cho 4 để tìm ra độ dài một cạnh.
• Dạng 3: Bài toán liên quan đến thực tế: Các bài toán này thường mô tả các tình huống thực tế, yêu cầu bạn vận dụng kiến thức về chu vi để giải quyết vấn đề. Ví dụ: tính lượng vật liệu cần thiết để làm khung tranh hình vuông, tính số mét dây thép gai cần để rào một khu đất hình vuông,…

2. Bí Quyết Tính Chu Vi Hình Vuông Nâng Cao: Mối Liên Hệ Với Các Yếu Tố Khác

2.1 Mối liên hệ giữa chu vi và diện tích hình vuông

Chu vi và diện tích là hai khái niệm quan trọng liên quan đến hình vuông. Diện tích hình vuông được tính bằng công thức:

Diện tích = Độ dài cạnh x Độ dài cạnh = a x a

Hoặc:

S = a²

Trong đó:

• S là diện tích hình vuông
• a là độ dài một cạnh của hình vuông

Tuy chu vi và diện tích là hai đại lượng khác nhau, chúng có mối liên hệ mật thiết với nhau thông qua độ dài cạnh. Nếu biết một trong hai đại lượng này, bạn có thể tìm ra đại lượng còn lại.

Ví dụ: Nếu một hình vuông có diện tích là 36cm², ta có thể tìm ra độ dài cạnh bằng cách lấy căn bậc hai của 36, tức là 6cm. Sau đó, ta có thể tính chu vi bằng công thức C = 6cm x 4 = 24cm.

2.2 Mối liên hệ giữa chu vi và đường chéo hình vuông

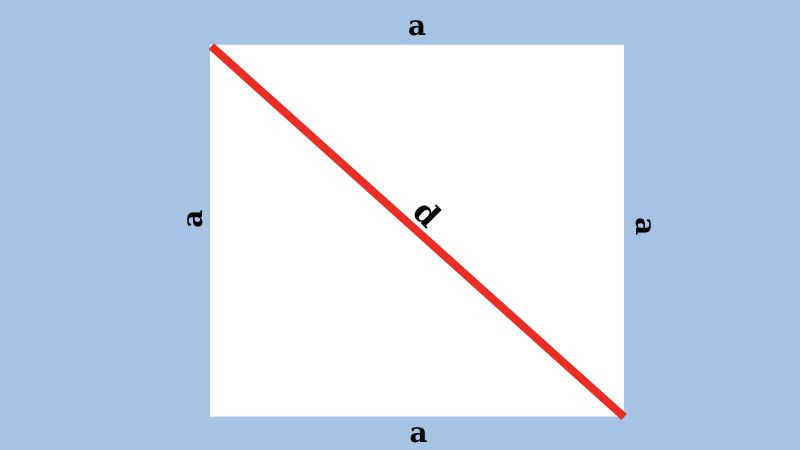
Đường chéo của hình vuông là đoạn thẳng nối hai đỉnh đối diện. Đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau. Độ dài đường chéo có thể được tính bằng công thức:

Đường chéo = Độ dài cạnh x √2

Hoặc:

d = a√2

Trong đó:

• d là độ dài đường chéo
• a là độ dài một cạnh của hình vuông

Tương tự như diện tích, đường chéo cũng có mối liên hệ với chu vi thông qua độ dài cạnh. Nếu biết độ dài đường chéo, bạn có thể tìm ra độ dài cạnh và từ đó tính được chu vi.

Ví dụ: Nếu một hình vuông có đường chéo dài 8√2 cm, ta có thể tìm ra độ dài cạnh bằng cách chia độ dài đường chéo cho √2, tức là 8cm. Sau đó, ta có thể tính chu vi bằng công thức C = 8cm x 4 = 32cm.

2.3 Ứng dụng công thức tính chu vi hình vuông trong giải toán hình học

Công thức tính chu vi hình vuông không chỉ hữu ích trong các bài toán đơn giản mà còn được ứng dụng rộng rãi trong các bài toán hình học phức tạp hơn. Ví dụ:

• Tính chu vi của hình ghép từ nhiều hình vuông.
• Tìm độ dài cạnh của hình vuông khi biết chu vi của một hình khác có liên quan.
• Chứng minh các tính chất hình học liên quan đến hình vuông và chu vi.

Để giải quyết các bài toán này, bạn cần nắm vững công thức tính chu vi, diện tích, đường chéo và các tính chất của hình vuông. Đồng thời, bạn cần rèn luyện kỹ năng phân tích, suy luận và vận dụng kiến thức một cách linh hoạt.

3. Lưu Ý Quan Trọng Khi Tính Chu Vi Hình Vuông Để Tránh Mắc Lỗi

3.1 Nhầm lẫn giữa chu vi và diện tích

Đây là lỗi phổ biến mà nhiều người mắc phải. Chu vi là độ dài đường bao quanh hình vuông, còn diện tích là phần bề mặt bên trong hình vuông. Hãy nhớ rằng chu vi được đo bằng đơn vị chiều dài (cm, m, km,…), còn diện tích được đo bằng đơn vị diện tích (cm², m², km²,…).

Để tránh nhầm lẫn, hãy luôn xác định rõ yêu cầu của bài toán là tính chu vi hay diện tích. Đọc kỹ đề bài và gạch chân những từ khóa quan trọng để không bị lạc đề.

3.2 Sai đơn vị đo

Khi tính chu vi, cần đảm bảo rằng tất cả các độ dài đều được đo bằng cùng một đơn vị. Nếu đề bài cho độ dài cạnh bằng mét và yêu cầu tính chu vi bằng centimet, bạn cần đổi mét sang centimet trước khi thực hiện phép tính.

Ví dụ: Nếu cạnh hình vuông là 2m, ta cần đổi 2m = 200cm. Sau đó, ta tính chu vi: C = 200cm x 4 = 800cm.

3.3 Tính toán sai

Dù công thức tính chu vi rất đơn giản, bạn vẫn có thể mắc lỗi nếu tính toán ẩu. Hãy cẩn thận khi thực hiện phép nhân và kiểm tra lại kết quả để đảm bảo tính chính xác.

Nếu có thể, hãy sử dụng máy tính để tránh sai sót. Tuy nhiên, đừng quá phụ thuộc vào máy tính mà quên đi cách tính nhẩm và ước lượng kết quả.

3.4 Bỏ qua các yếu tố khác trong bài toán

Trong một số bài toán phức tạp, việc tính chu vi chỉ là một phần nhỏ trong toàn bộ bài toán. Bạn cần đọc kỹ đề bài, phân tích các yếu tố liên quan và tìm ra mối liên hệ giữa chúng để giải quyết bài toán một cách trọn vẹn.

Ví dụ: Một bài toán có thể yêu cầu bạn tính diện tích của một hình chữ nhật có chiều dài bằng chu vi của một hình vuông cho trước. Để giải bài toán này, bạn cần tính chu vi của hình vuông trước, sau đó sử dụng kết quả đó để tính diện tích hình chữ nhật.

4. Ứng Dụng Thực Tế Của Việc Tính Chu Vi Hình Vuông Trong Đời Sống

4.1 Trong xây dựng và kiến trúc

Trong xây dựng và kiến trúc, việc tính chu vi hình vuông được sử dụng để tính toán lượng vật liệu cần thiết để xây dựng các công trình có hình dạng vuông, chẳng hạn như:

• Tính lượng gạch cần để xây một bức tường hình vuông.
• Tính lượng gỗ cần để làm khung cửa sổ hình vuông.
• Tính lượng sơn cần để sơn một căn phòng hình vuông.

Ngoài ra, việc tính chu vi còn giúp các kiến trúc sư và kỹ sư xác định kích thước và vị trí của các yếu tố kiến trúc, đảm bảo tính thẩm mỹ và độ bền vững của công trình.

4.2 Trong thiết kế nội thất

Trong thiết kế nội thất, việc tính chu vi hình vuông được sử dụng để:

• Tính kích thước của các vật dụng nội thất hình vuông, chẳng hạn như bàn, ghế, tủ,…
• Xác định vị trí đặt các vật dụng nội thất trong phòng, đảm bảo sự cân đối và hài hòa.
• Tính lượng vật liệu cần thiết để bọc hoặc trang trí các vật dụng nội thất.

Ví dụ: Khi chọn mua một chiếc bàn hình vuông cho phòng khách, bạn cần tính toán kích thước của bàn sao cho phù hợp với diện tích phòng và không gian xung quanh.

4.3 Trong nông nghiệp

Trong nông nghiệp, việc tính chu vi hình vuông được sử dụng để:

• Tính lượng vật liệu cần thiết để làm hàng rào bảo vệ khu đất hình vuông.
• Xác định khoảng cách giữa các cây trồng trong một khu vườn hình vuông.
• Tính diện tích của một khu đất hình vuông để ước lượng năng suất cây trồng.

Ví dụ: Một người nông dân muốn rào một khu đất trồng rau hình vuông để bảo vệ rau khỏi gia súc. Anh ta cần tính chu vi của khu đất để biết cần bao nhiêu mét lưới rào.

4.4 Trong đời sống hàng ngày

Ngoài các lĩnh vực trên, việc tính chu vi hình vuông còn có nhiều ứng dụng trong đời sống hàng ngày, chẳng hạn như:

• Tính lượng ren cần để viền một chiếc khăn tay hình vuông.
• Tính lượng giấy gói quà cần để gói một hộp quà hình vuông.
• Ước lượng khoảng cách đi bộ xung quanh một khu vực hình vuông.

5. Mẹo Học Thuộc Và Áp Dụng Công Thức Tính Chu Vi Hình Vuông Hiệu Quả

5.1 Học thuộc công thức bằng cách liên tưởng

Thay vì học thuộc một cách máy móc, hãy liên tưởng công thức tính chu vi hình vuông với những hình ảnh quen thuộc trong cuộc sống. Ví dụ, bạn có thể hình dung một chiếc bánh pizza hình vuông được chia thành 4 phần bằng nhau. Chu vi của chiếc bánh pizza chính là tổng độ dài của 4 cạnh.

5.2 Luyện tập thường xuyên với các bài tập đa dạng

Cách tốt nhất để nắm vững công thức tính chu vi hình vuông là luyện tập thường xuyên với các bài tập đa dạng. Bắt đầu với các bài tập cơ bản, sau đó chuyển sang các bài tập phức tạp hơn. Đừng ngại thử sức với những bài toán khó, vì chúng sẽ giúp bạn rèn luyện tư duy và kỹ năng giải quyết vấn đề.

Bạn có thể tìm kiếm các bài tập về chu vi hình vuông trên sách giáo khoa, sách bài tập, hoặc trên các trang web giáo dục như tic.edu.vn.

5.3 Áp dụng kiến thức vào thực tế

Hãy thử áp dụng kiến thức về chu vi hình vuông vào các tình huống thực tế trong cuộc sống. Ví dụ, bạn có thể đo độ dài cạnh của một chiếc bàn hình vuông và tính chu vi của nó. Hoặc bạn có thể ước lượng chu vi của một khu đất hình vuông khi đi ngang qua nó.

Việc áp dụng kiến thức vào thực tế sẽ giúp bạn hiểu rõ hơn về ý nghĩa của công thức và ghi nhớ nó lâu hơn.

5.4 Tham gia các hoạt động học tập nhóm

Học tập nhóm là một cách hiệu quả để củng cố kiến thức và học hỏi kinh nghiệm từ người khác. Hãy tham gia các nhóm học tập với bạn bè hoặc tham gia các diễn đàn trực tuyến để trao đổi kiến thức và giải đáp thắc mắc.

Bạn cũng có thể tham gia các trò chơi hoặc hoạt động tương tác liên quan đến chu vi hình vuông để làm cho việc học tập trở nên thú vị hơn.

6. Đường Chéo Hình Vuông: Mở Rộng Kiến Thức Và Ứng Dụng

6.1 Đường chéo hình vuông là gì?

Đường chéo của một hình vuông là đoạn thẳng nối hai đỉnh đối diện của hình vuông đó. Mỗi hình vuông có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

6.2 Công thức tính đường chéo hình vuông

Độ dài đường chéo của hình vuông có thể được tính bằng công thức:

d = a√2

Trong đó:

• d là độ dài đường chéo
• a là độ dài một cạnh của hình vuông

Công thức này xuất phát từ định lý Pythagoras, vì đường chéo chia hình vuông thành hai tam giác vuông cân bằng nhau.

6.3 Mối liên hệ giữa đường chéo và chu vi hình vuông

Như đã đề cập ở trên, đường chéo và chu vi hình vuông có mối liên hệ với nhau thông qua độ dài cạnh. Nếu biết độ dài đường chéo, bạn có thể tìm ra độ dài cạnh bằng cách chia độ dài đường chéo cho √2. Sau đó, bạn có thể tính chu vi bằng công thức C = a x 4.

6.4 Ứng dụng của đường chéo hình vuông

Đường chéo hình vuông có nhiều ứng dụng trong các lĩnh vực khác nhau, chẳng hạn như:

• Trong xây dựng: Xác định kích thước và vị trí của các yếu tố kiến trúc.
• Trong thiết kế: Tạo ra các đường chéo trong bố cục của các vật phẩm nội thất.
• Trong hình học: Giải quyết các bài toán liên quan đến kích thước và vị trí của các hình vuông.

7. Bài Tập Vận Dụng Về Chu Vi Và Đường Chéo Hình Vuông (Có Đáp Án Chi Tiết)

Để giúp bạn củng cố kiến thức và rèn luyện kỹ năng giải toán, dưới đây là một số bài tập vận dụng về chu vi và đường chéo hình vuông, kèm theo đáp án chi tiết:

Bài 1: Một hình vuông có chu vi là 36cm. Tính độ dài cạnh của hình vuông đó.

Đáp án:

Độ dài cạnh của hình vuông là: 36cm / 4 = 9cm

Bài 2: Một hình vuông có cạnh dài 5cm. Tính diện tích và đường chéo của hình vuông đó.

Đáp án:

Diện tích của hình vuông là: 5cm x 5cm = 25cm²

Độ dài đường chéo của hình vuông là: 5cm x √2 ≈ 7.07cm

Bài 3: Một mảnh vườn hình vuông có chu vi là 64m. Người ta muốn làm hàng rào bao quanh mảnh vườn. Hỏi cần bao nhiêu mét hàng rào?

Đáp án:

Số mét hàng rào cần dùng chính là chu vi của mảnh vườn, tức là 64m.

Bài 4: Một hình vuông có đường chéo dài 10√2 cm. Tính chu vi của hình vuông đó.

Đáp án:

Độ dài cạnh của hình vuông là: 10√2 cm / √2 = 10cm

Chu vi của hình vuông là: 10cm x 4 = 40cm

Bài 5: Một hình chữ nhật có chiều dài bằng chu vi của một hình vuông có cạnh dài 4cm, chiều rộng bằng một nửa chiều dài. Tính diện tích của hình chữ nhật đó.

Đáp án:

Chu vi của hình vuông là: 4cm x 4 = 16cm

Chiều dài của hình chữ nhật là: 16cm

Chiều rộng của hình chữ nhật là: 16cm / 2 = 8cm

Diện tích của hình chữ nhật là: 16cm x 8cm = 128cm²

8. Các Nguồn Tài Liệu Tham Khảo Bổ Ích Về Hình Học Và Toán Học

Để nâng cao kiến thức và kỹ năng về hình học và toán học, bạn có thể tham khảo các nguồn tài liệu sau:

• Sách giáo khoa và sách bài tập toán các cấp: Đây là nguồn tài liệu cơ bản và quan trọng nhất, cung cấp đầy đủ kiến thức và bài tập từ dễ đến khó.
• Sách tham khảo toán: Các loại sách này cung cấp kiến thức nâng cao, các dạng bài tập phức tạp và các phương pháp giải toán hiệu quả.
• Các trang web giáo dục trực tuyến: Có rất nhiều trang web cung cấp các bài giảng, bài tập và tài liệu tham khảo về toán học, chẳng hạn như Khan Academy, VnDoc, VietJack,…
• Các diễn đàn và nhóm học tập trực tuyến: Đây là nơi bạn có thể trao đổi kiến thức, học hỏi kinh nghiệm và giải đáp thắc mắc với những người cùng sở thích.
• Các ứng dụng học toán trên điện thoại: Các ứng dụng này cung cấp các bài tập tương tác, trò chơi và công cụ hỗ trợ học tập, giúp bạn học toán một cách thú vị và hiệu quả.

9. Lời Khuyên Từ Chuyên Gia: Học Toán Như Thế Nào Để Đạt Hiệu Quả Cao Nhất

Để học toán đạt hiệu quả cao nhất, bạn cần:

• Nắm vững kiến thức cơ bản: Đây là nền tảng để bạn tiếp thu kiến thức nâng cao và giải quyết các bài toán phức tạp.
• Luyện tập thường xuyên: Thực hành giải bài tập là cách tốt nhất để củng cố kiến thức và rèn luyện kỹ năng.
• Học hỏi từ sai lầm: Đừng sợ sai, vì sai lầm là cơ hội để bạn học hỏi và tiến bộ.
• Tìm kiếm sự giúp đỡ khi cần thiết: Nếu gặp khó khăn, đừng ngại hỏi thầy cô, bạn bè hoặc tham gia các nhóm học tập.
• Học tập một cách chủ động và tích cực: Tự giác tìm tòi, khám phá và đặt câu hỏi để hiểu sâu sắc vấn đề.
• Tìm niềm vui trong học tập: Hãy coi toán học là một thử thách thú vị, thay vì một môn học khô khan và nhàm chán.

Theo Tiến sĩ Nguyễn Văn A, giảng viên khoa Toán học tại Đại học Quốc gia Hà Nội, việc kết hợp lý thuyết và thực hành là chìa khóa để thành công trong học toán.

10. Tic.edu.vn: Nguồn Tài Liệu Học Tập Phong Phú Và Cộng Đồng Hỗ Trợ Đắc Lực

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng và đáng tin cậy? Bạn mất thời gian tổng hợp thông tin giáo dục từ nhiều nguồn khác nhau? Bạn cần các công cụ hỗ trợ học tập hiệu quả để nâng cao năng suất? Bạn mong muốn kết nối với cộng đồng học tập để trao đổi kiến thức và kinh nghiệm?

Hãy đến với tic.edu.vn! Chúng tôi cung cấp:

• Nguồn tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng.
• Thông tin giáo dục mới nhất và chính xác.
• Các công cụ hỗ trợ học tập trực tuyến hiệu quả (ví dụ: công cụ ghi chú, quản lý thời gian).
• Cộng đồng học tập trực tuyến sôi nổi để bạn có thể tương tác và học hỏi lẫn nhau.
• Các khóa học và tài liệu giúp phát triển kỹ năng mềm và kỹ năng chuyên môn.

tic.edu.vn cam kết mang đến cho bạn trải nghiệm học tập tốt nhất, giúp bạn chinh phục mọi thử thách và đạt được thành công trong học tập và sự nghiệp.

Đừng chần chừ nữa, hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả!

Email: [email protected]

Trang web: tic.edu.vn

FAQ – Giải Đáp Thắc Mắc Về Tìm Kiếm Tài Liệu Học Tập Trên Tic.edu.vn

1. Tic.edu.vn cung cấp những loại tài liệu học tập nào?

tic.edu.vn cung cấp đa dạng các loại tài liệu học tập từ lớp 1 đến lớp 12, bao gồm sách giáo khoa, sách bài tập, đề thi, bài giảng, tài liệu tham khảo, v.v.

2. Làm thế nào để tìm kiếm tài liệu trên Tic.edu.vn?

Bạn có thể tìm kiếm tài liệu bằng cách sử dụng thanh tìm kiếm trên trang web, hoặc duyệt theo danh mục môn học, lớp học.

3. Tài liệu trên Tic.edu.vn có đáng tin cậy không?

Chúng tôi kiểm duyệt kỹ lưỡng tất cả các tài liệu trước khi đăng tải để đảm bảo tính chính xác và độ tin cậy.

4. Tôi có thể đóng góp tài liệu cho Tic.edu.vn không?

Có, chúng tôi luôn hoan nghênh sự đóng góp của bạn. Vui lòng liên hệ với chúng tôi qua email để biết thêm chi tiết.

5. Tic.edu.vn có công cụ hỗ trợ học tập trực tuyến nào?

Chúng tôi cung cấp các công cụ như công cụ ghi chú, quản lý thời gian, v.v. để giúp bạn học tập hiệu quả hơn.

6. Làm thế nào để tham gia cộng đồng học tập trên Tic.edu.vn?

Bạn có thể tham gia bằng cách đăng ký tài khoản và tham gia các diễn đàn, nhóm học tập.

7. Tic.edu.vn có khóa học trực tuyến không?

Có, chúng tôi cung cấp các khóa học trực tuyến về nhiều chủ đề khác nhau.

8. Tôi có thể liên hệ với Tic.edu.vn bằng cách nào?

Bạn có thể liên hệ với chúng tôi qua email hoặc qua các kênh mạng xã hội.

9. Tic.edu.vn có thu phí không?

Một số tài liệu và khóa học có thể yêu cầu trả phí, nhưng chúng tôi cũng cung cấp nhiều tài liệu miễn phí.

10. tic.edu.vn có phiên bản dành cho điện thoại không?

Chúng tôi đang phát triển phiên bản dành cho điện thoại để bạn có thể truy cập dễ dàng hơn.