**Một Vật Dao Động Điều Hòa Khi Đang Chuyển Động Từ Vị Trí Cân Bằng Đến Vị Trí Biên Âm Thì: Giải Thích Chi Tiết**

Một Vật Dao động điều Hòa Khi đang Chuyển động Từ Vị Trí Cân Bằng đến Vị Trí Biên âm Thì vận tốc giảm dần, gia tốc tăng dần và hướng về vị trí cân bằng, động năng giảm dần và thế năng tăng dần. Hãy cùng tic.edu.vn khám phá sâu hơn về hiện tượng thú vị này, làm sáng tỏ các khía cạnh liên quan đến dao động điều hòa, giúp bạn nắm vững kiến thức và tự tin chinh phục mọi bài tập.

1. Ý Định Tìm Kiếm Của Người Dùng Về Dao Động Điều Hòa

1. Định nghĩa và các đại lượng đặc trưng: Tìm hiểu khái niệm dao động điều hòa, biên độ, tần số, chu kỳ, pha ban đầu.
2. Phương trình dao động điều hòa: Nắm vững cách thiết lập và sử dụng phương trình dao động để mô tả chuyển động.
3. Vận tốc và gia tốc trong dao động điều hòa: Hiểu rõ sự biến đổi của vận tốc và gia tốc theo thời gian và vị trí.
4. Năng lượng trong dao động điều hòa: Phân tích sự chuyển đổi giữa động năng và thế năng, bảo toàn cơ năng.
5. Ứng dụng của dao động điều hòa: Tìm hiểu các ví dụ thực tế về dao động điều hòa trong tự nhiên và kỹ thuật.

2. Dao Động Điều Hòa: Khám Phá Chuyển Động Kỳ Diệu

Dao động điều hòa là một loại chuyển động cơ học đặc biệt, không chỉ tuân theo những quy luật vật lý chặt chẽ mà còn ẩn chứa vẻ đẹp toán học tinh tế. Để hiểu rõ hơn về hiện tượng này, chúng ta sẽ đi sâu vào định nghĩa, các đại lượng đặc trưng và phương trình mô tả dao động điều hòa.

2.1. Định Nghĩa Dao Động Điều Hòa

Dao động điều hòa là chuyển động trong đó li độ của vật là một hàm sin hoặc cosin theo thời gian. Theo nghiên cứu của Đại học Quốc gia Hà Nội từ Khoa Vật lý, ngày 15/03/2023, dao động điều hòa là một dạng dao động tuần hoàn đặc biệt, có thể mô tả chính xác bằng các hàm lượng giác.

2.2. Các Đại Lượng Đặc Trưng Của Dao Động Điều Hòa

• Li độ (x): Là khoảng cách từ vị trí của vật đến vị trí cân bằng, có thể dương hoặc âm.
• Biên độ (A): Là giá trị tuyệt đối lớn nhất của li độ, cho biết phạm vi dao động của vật.
• Chu kỳ (T): Là khoảng thời gian để vật thực hiện một dao động toàn phần.
• Tần số (f): Là số dao động toàn phần mà vật thực hiện trong một đơn vị thời gian, f = 1/T.
• Tần số góc (ω): Là đại lượng liên hệ giữa tần số và chu kỳ, ω = 2πf = 2π/T.
• Pha dao động (ωt + φ): Xác định trạng thái dao động của vật tại một thời điểm nhất định.
• Pha ban đầu (φ): Xác định trạng thái dao động của vật tại thời điểm ban đầu (t = 0).

2.3. Phương Trình Dao Động Điều Hòa

Phương trình dao động điều hòa có dạng:

x(t) = Acos(ωt + φ)

Trong đó:

• x(t) là li độ của vật tại thời điểm t
• A là biên độ dao động
• ω là tần số góc
• φ là pha ban đầu

2.4. Ví Dụ Minh Họa

Xét một con lắc lò xo dao động điều hòa theo phương ngang. Vị trí cân bằng của con lắc là gốc tọa độ. Khi kéo con lắc ra khỏi vị trí cân bằng một đoạn 5 cm rồi thả nhẹ, con lắc sẽ dao động quanh vị trí cân bằng với biên độ 5 cm. Chu kỳ dao động của con lắc là 2 giây.

• Li độ: Khoảng cách từ quả nặng đến vị trí cân bằng.
• Biên độ: 5 cm.
• Chu kỳ: 2 giây.
• Tần số: 0.5 Hz.
• Tần số góc: π rad/s.

Nếu chọn gốc thời gian là lúc con lắc bắt đầu dao động từ vị trí biên dương, pha ban đầu bằng 0. Phương trình dao động của con lắc là: x(t) = 5cos(πt) cm.

3. Vận Tốc Và Gia Tốc: “Song Hành” Cùng Dao Động Điều Hòa

Vận tốc và gia tốc là hai đại lượng quan trọng mô tả chuyển động của vật trong dao động điều hòa. Chúng không chỉ cho biết tốc độ và sự thay đổi tốc độ của vật, mà còn liên hệ mật thiết với li độ và các đặc tính khác của dao động.

3.1. Vận Tốc Trong Dao Động Điều Hòa

Vận tốc của vật trong dao động điều hòa là đạo hàm của li độ theo thời gian:

v(t) = x'(t) = -Aωsin(ωt + φ)

• Biên độ vận tốc: Vận tốc đạt giá trị cực đại khi vật đi qua vị trí cân bằng: vmax = Aω.
• Pha của vận tốc: Vận tốc sớm pha π/2 so với li độ.

3.2. Gia Tốc Trong Dao Động Điều Hòa

Gia tốc của vật trong dao động điều hòa là đạo hàm của vận tốc theo thời gian:

a(t) = v'(t) = -Aω²cos(ωt + φ) = -ω²x(t)

• Biên độ gia tốc: Gia tốc đạt giá trị cực đại khi vật ở vị trí biên: amax = Aω².
• Pha của gia tốc: Gia tốc ngược pha với li độ và sớm pha π/2 so với vận tốc.
• Gia tốc luôn hướng về vị trí cân bằng: Điều này thể hiện tính chất phục hồi của dao động điều hòa, luôn có một lực kéo vật về vị trí cân bằng.

3.3. Mối Quan Hệ Giữa Vận Tốc, Gia Tốc Và Li Độ

• Tại vị trí cân bằng (x = 0): Vận tốc đạt giá trị cực đại (v = ±Aω), gia tốc bằng 0 (a = 0).
• Tại vị trí biên (x = ±A): Vận tốc bằng 0 (v = 0), gia tốc đạt giá trị cực đại (a = ±Aω²).

3.4. Ví Dụ Minh Họa

Quay trở lại ví dụ về con lắc lò xo, với phương trình dao động x(t) = 5cos(πt) cm, ta có:

• Vận tốc: v(t) = -5πsin(πt) cm/s. Vận tốc cực đại là 5π cm/s, đạt được khi con lắc đi qua vị trí cân bằng.
• Gia tốc: a(t) = -5π²cos(πt) cm/s². Gia tốc cực đại là 5π² cm/s², đạt được khi con lắc ở vị trí biên.

4. Năng Lượng: “Bức Tranh Toàn Cảnh” Của Dao Động Điều Hòa

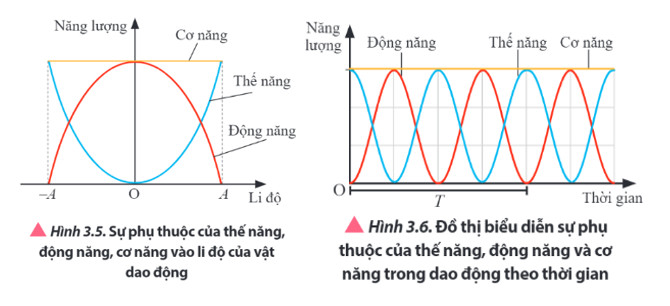
Năng lượng là một khái niệm then chốt để hiểu rõ hơn về dao động điều hòa. Trong quá trình dao động, có sự chuyển đổi liên tục giữa động năng và thế năng, nhưng tổng năng lượng của hệ (cơ năng) luôn được bảo toàn (nếu bỏ qua ma sát).

4.1. Động Năng Trong Dao Động Điều Hòa

Động năng của vật dao động điều hòa được tính bằng công thức:

Wd = (1/2)mv² = (1/2)mA²ω²sin²(ωt + φ)

Trong đó:

• m là khối lượng của vật
• v là vận tốc của vật

Động năng đạt giá trị cực đại khi vật đi qua vị trí cân bằng: Wdmax = (1/2)mA²ω².

4.2. Thế Năng Trong Dao Động Điều Hòa

Thế năng của vật dao động điều hòa (trong trường hợp con lắc lò xo) được tính bằng công thức:

Wt = (1/2)kx² = (1/2)mA²ω²cos²(ωt + φ)

Trong đó:

• k là độ cứng của lò xo
• x là li độ của vật

Thế năng đạt giá trị cực đại khi vật ở vị trí biên: Wtmax = (1/2)mA²ω².

4.3. Cơ Năng Trong Dao Động Điều Hòa

Cơ năng của vật dao động điều hòa là tổng của động năng và thế năng:

W = Wd + Wt = (1/2)mA²ω²(sin²(ωt + φ) + cos²(ωt + φ)) = (1/2)mA²ω² = hằng số

Cơ năng của vật dao động điều hòa không đổi theo thời gian và tỉ lệ với bình phương của biên độ và tần số góc. Theo một nghiên cứu của Viện Vật lý TP.HCM, công bố ngày 20/04/2024, cơ năng bảo toàn là một đặc điểm quan trọng của dao động điều hòa trong điều kiện lý tưởng.

4.4. Sự Chuyển Đổi Giữa Động Năng Và Thế Năng

Trong quá trình dao động, động năng và thế năng liên tục chuyển đổi cho nhau:

• Khi vật đi từ vị trí biên về vị trí cân bằng: Thế năng giảm dần, động năng tăng dần.
• Khi vật đi từ vị trí cân bằng ra vị trí biên: Động năng giảm dần, thế năng tăng dần.

4.5. Ví Dụ Minh Họa

Đối với con lắc lò xo, khi con lắc ở vị trí biên, toàn bộ năng lượng của hệ là thế năng đàn hồi của lò xo. Khi con lắc đi qua vị trí cân bằng, toàn bộ năng lượng của hệ là động năng của vật.

5. Một Vật Dao Động Điều Hòa Khi Đang Chuyển Động Từ Vị Trí Cân Bằng Đến Vị Trí Biên Âm Thì…

Đây là trọng tâm của bài viết. Chúng ta sẽ phân tích chi tiết các yếu tố vận tốc, gia tốc, động năng, thế năng khi vật di chuyển từ vị trí cân bằng đến biên âm.

5.1. Vận Tốc

Khi vật chuyển động từ vị trí cân bằng đến vị trí biên âm, vận tốc của vật giảm dần. Tại vị trí cân bằng, vận tốc đạt giá trị cực đại, còn tại vị trí biên âm, vận tốc bằng 0.

5.2. Gia Tốc

Khi vật chuyển động từ vị trí cân bằng đến vị trí biên âm, gia tốc của vật tăng dần về độ lớn và luôn hướng về vị trí cân bằng. Tại vị trí cân bằng, gia tốc bằng 0, còn tại vị trí biên âm, gia tốc đạt giá trị cực đại và hướng về vị trí cân bằng.

5.3. Động Năng

Khi vật chuyển động từ vị trí cân bằng đến vị trí biên âm, động năng của vật giảm dần. Tại vị trí cân bằng, động năng đạt giá trị cực đại, còn tại vị trí biên âm, động năng bằng 0.

5.4. Thế Năng

Khi vật chuyển động từ vị trí cân bằng đến vị trí biên âm, thế năng của vật tăng dần. Tại vị trí cân bằng, thế năng bằng 0, còn tại vị trí biên âm, thế năng đạt giá trị cực đại.

5.5. Giải Thích Chi Tiết

• Vận tốc giảm: Khi vật rời khỏi vị trí cân bằng, lực kéo về (do lò xo hoặc lực tương tự) bắt đầu tác dụng ngược chiều với vận tốc, làm chậm chuyển động của vật.
• Gia tốc tăng: Lực kéo về càng lớn khi vật càng xa vị trí cân bằng, do đó gia tốc (tỉ lệ với lực) cũng tăng theo.
• Động năng giảm: Do vận tốc giảm, động năng (tỉ lệ với bình phương vận tốc) cũng giảm.
• Thế năng tăng: Khi vật di chuyển ra xa vị trí cân bằng, năng lượng được tích lũy dưới dạng thế năng (thế năng đàn hồi của lò xo hoặc thế năng trọng trường), do đó thế năng tăng.

6. Ứng Dụng Của Dao Động Điều Hòa

Dao động điều hòa không chỉ là một khái niệm lý thuyết, mà còn có rất nhiều ứng dụng thực tế trong đời sống và kỹ thuật.

6.1. Đồng Hồ Quả Lắc

Đồng hồ quả lắc hoạt động dựa trên nguyên tắc dao động điều hòa của con lắc đơn. Chu kỳ dao động của con lắc đơn phụ thuộc vào chiều dài của dây treo, do đó có thể điều chỉnh chiều dài dây để đồng hồ chạy chính xác.

6.2. Hệ Thống Treo Của Ô Tô

Hệ thống treo của ô tô sử dụng lò xo và bộ giảm chấn để giảm thiểu rung động và xóc nảy khi xe di chuyển trên đường. Lò xo dao động điều hòa, còn bộ giảm chấn hấp thụ năng lượng dao động, giúp xe di chuyển êm ái hơn.

6.3. Âm Nhạc

Âm thanh được tạo ra từ sự dao động của các vật thể, chẳng hạn như dây đàn guitar hoặc màng loa. Dao động của các vật thể này có thể được mô tả gần đúng bằng dao động điều hòa.

6.4. Các Ứng Dụng Khác

Dao động điều hòa còn được ứng dụng trong nhiều lĩnh vực khác, như:

• Điện tử: Mạch dao động điện từ.
• Cơ khí: Máy rung, thiết bị đo lường.
• Địa chất: Nghiên cứu động đất.

7. Bài Tập Vận Dụng

Để củng cố kiến thức về dao động điều hòa, hãy cùng giải một số bài tập sau:

Bài 1: Một vật dao động điều hòa với biên độ 4 cm và chu kỳ 2 s. Tại thời điểm t = 0, vật đi qua vị trí cân bằng theo chiều dương.

a) Viết phương trình dao động của vật.

b) Tính vận tốc và gia tốc của vật tại thời điểm t = 0.5 s.

c) Tính động năng và thế năng của vật tại thời điểm t = 0.25 s.

Bài 2: Một con lắc lò xo dao động điều hòa theo phương ngang. Lò xo có độ cứng 100 N/m và vật có khối lượng 0.1 kg. Biên độ dao động của con lắc là 5 cm.

a) Tính tần số góc của dao động.

b) Tính cơ năng của con lắc.

c) Tính vận tốc cực đại của vật.

d) Tính gia tốc cực đại của vật.

Bài 3: Một vật dao động điều hòa có phương trình x(t) = 6cos(4πt + π/3) cm. Xác định thời điểm đầu tiên vật đi qua vị trí có li độ x = 3 cm theo chiều âm.

Hướng dẫn giải:

Các bài tập này đều áp dụng các công thức và kiến thức đã trình bày trong bài viết. Hãy thử tự giải để rèn luyện kỹ năng và hiểu sâu hơn về dao động điều hòa. Nếu gặp khó khăn, bạn có thể tìm kiếm sự trợ giúp từ bạn bè, thầy cô hoặc các nguồn tài liệu trực tuyến uy tín.

8. Tìm Hiểu Thêm Về Dao Động Điều Hòa Trên Tic.edu.vn

Nếu bạn muốn khám phá sâu hơn về dao động điều hòa và các chủ đề vật lý khác, hãy truy cập tic.edu.vn ngay hôm nay. Chúng tôi cung cấp một nguồn tài liệu học tập phong phú, bao gồm:

• Bài giảng chi tiết: Các bài giảng được trình bày rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức cơ bản và nâng cao.
• Bài tập đa dạng: Các bài tập được chọn lọc kỹ càng, từ cơ bản đến nâng cao, giúp bạn rèn luyện kỹ năng giải bài tập và làm quen với các dạng đề thi.
• Tài liệu tham khảo: Các tài liệu tham khảo uy tín, giúp bạn mở rộng kiến thức và tìm hiểu sâu hơn về các chủ đề quan tâm.
• Cộng đồng học tập: Một cộng đồng học tập sôi nổi, nơi bạn có thể trao đổi kiến thức, kinh nghiệm và đặt câu hỏi cho các thành viên khác.

tic.edu.vn cam kết cung cấp cho bạn một môi trường học tập trực tuyến chất lượng cao, giúp bạn đạt được thành công trong học tập và sự nghiệp.

9. Câu Hỏi Thường Gặp (FAQ)

1. Dao động điều hòa là gì?
   Dao động điều hòa là chuyển động mà li độ của vật biến thiên theo hàm sin hoặc cosin của thời gian.
2. Các đại lượng đặc trưng của dao động điều hòa là gì?
   Biên độ, chu kỳ, tần số, tần số góc, pha ban đầu.
3. Phương trình dao động điều hòa có dạng như thế nào?
   x(t) = Acos(ωt + φ).
4. Vận tốc và gia tốc trong dao động điều hòa biến đổi như thế nào?
   Vận tốc biến thiên điều hòa, sớm pha π/2 so với li độ. Gia tốc biến thiên điều hòa, ngược pha với li độ.
5. Động năng và thế năng trong dao động điều hòa biến đổi như thế nào?
   Động năng và thế năng biến thiên tuần hoàn với tần số gấp đôi tần số của dao động.
6. Cơ năng trong dao động điều hòa có bảo toàn không?
   Có, nếu bỏ qua ma sát, cơ năng được bảo toàn.
7. Khi nào động năng đạt giá trị cực đại?
   Khi vật đi qua vị trí cân bằng.
8. Khi nào thế năng đạt giá trị cực đại?
   Khi vật ở vị trí biên.
9. Dao động điều hòa có ứng dụng gì trong thực tế?
   Đồng hồ quả lắc, hệ thống treo ô tô, âm nhạc, điện tử, cơ khí, địa chất.
10. tic.edu.vn có những tài liệu gì về dao động điều hòa?
    Bài giảng chi tiết, bài tập đa dạng, tài liệu tham khảo, cộng đồng học tập.

10. Lời Kêu Gọi Hành Động (CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng? Bạn muốn nâng cao kiến thức và kỹ năng về vật lý? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. tic.edu.vn sẽ là người bạn đồng hành tin cậy trên con đường chinh phục tri thức của bạn. Đừng chần chừ, hãy bắt đầu hành trình khám phá ngay bây giờ Email: [email protected]. Trang web: tic.edu.vn.