**Mặt Bên Của Hình Lăng Trụ Đứng Tam Giác Là Gì?**

Mặt Bên Của Hình Lăng Trụ đứng Tam Giác Là hình chữ nhật và đây là yếu tố quan trọng để tính diện tích xung quanh cũng như thể tích của hình. Cùng tic.edu.vn khám phá chi tiết về cấu trúc, đặc điểm và ứng dụng của hình lăng trụ đứng tam giác, giúp bạn nắm vững kiến thức và tự tin giải mọi bài tập.

1. Hiểu Rõ Về Hình Lăng Trụ Đứng Tam Giác

1.1 Định Nghĩa Hình Lăng Trụ Đứng Tam Giác

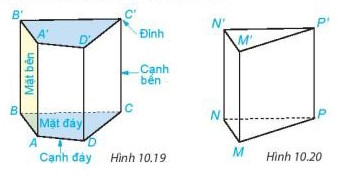
Hình lăng trụ đứng tam giác là một loại hình học không gian đặc biệt. Nó có hai mặt đáy là hai tam giác song song và bằng nhau. Các mặt bên của hình lăng trụ là các hình chữ nhật nối các cạnh tương ứng của hai đáy lại với nhau. Điểm đặc biệt của hình lăng trụ đứng là các cạnh bên vuông góc với mặt đáy, tạo thành hình dáng “đứng” vững chắc.

1.2 Cấu Trúc Chi Tiết Của Hình Lăng Trụ Đứng Tam Giác

Để hiểu rõ hơn về hình lăng trụ đứng tam giác, chúng ta cần nắm vững các thành phần cấu tạo của nó:

• Mặt đáy: Hình lăng trụ có hai mặt đáy là hai tam giác (có thể là tam giác đều, tam giác vuông, tam giác cân hoặc tam giác thường). Hai mặt đáy này song song và hoàn toàn bằng nhau.

• Mặt bên: Các mặt bên của hình lăng trụ đứng tam giác luôn là hình chữ nhật. Số lượng mặt bên tương ứng với số cạnh của tam giác đáy, tức là có ba mặt bên.

• Cạnh đáy: Các cạnh của tam giác đáy được gọi là cạnh đáy của hình lăng trụ.

• Cạnh bên: Các cạnh nối giữa hai mặt đáy và vuông góc với mặt đáy được gọi là cạnh bên. Các cạnh bên này có độ dài bằng nhau và bằng chiều cao của hình lăng trụ.

• Đỉnh: Các điểm giao nhau của các cạnh được gọi là đỉnh của hình lăng trụ.

Alt text: Hình lăng trụ đứng tam giác minh họa các thành phần mặt đáy, mặt bên, cạnh đáy, cạnh bên và chiều cao.

1.3 Phân Loại Hình Lăng Trụ Đứng Tam Giác

Hình lăng trụ đứng tam giác có thể được phân loại dựa trên hình dạng của tam giác đáy:

• Hình lăng trụ đứng tam giác đều: Đáy là tam giác đều.
• Hình lăng trụ đứng tam giác vuông: Đáy là tam giác vuông.
• Hình lăng trụ đứng tam giác cân: Đáy là tam giác cân.
• Hình lăng trụ đứng tam giác thường: Đáy là tam giác thường (không có tính chất đặc biệt).

Việc phân loại này giúp chúng ta dễ dàng nhận biết và áp dụng các công thức tính toán phù hợp cho từng loại hình lăng trụ.

2. Đặc Điểm Của Mặt Bên Hình Lăng Trụ Đứng Tam Giác

2.1 Hình Dạng Mặt Bên

Mỗi mặt bên của hình lăng trụ đứng tam giác là một hình chữ nhật. Điều này xuất phát từ định nghĩa của hình lăng trụ đứng, trong đó các cạnh bên phải vuông góc với mặt đáy.

2.2 Số Lượng Mặt Bên

Hình lăng trụ đứng tam giác có ba mặt bên, tương ứng với ba cạnh của tam giác đáy. Mỗi mặt bên kết nối một cạnh của tam giác đáy với cạnh tương ứng của tam giác đáy còn lại.

2.3 Tính Chất Của Mặt Bên

• Diện tích: Diện tích của mỗi mặt bên được tính bằng công thức diện tích hình chữ nhật: chiều dài nhân với chiều rộng. Trong trường hợp này, chiều dài là cạnh đáy của tam giác và chiều rộng là chiều cao của hình lăng trụ.
• Tính vuông góc: Các mặt bên vuông góc với mặt đáy, tạo nên tính chất “đứng” của hình lăng trụ.
• Vai trò: Các mặt bên đóng vai trò quan trọng trong việc tạo nên hình dạng và tính chất của hình lăng trụ. Chúng cũng là yếu tố cần thiết để tính diện tích xung quanh và diện tích toàn phần của hình lăng trụ.

2.4 Liên Hệ Giữa Mặt Bên và Các Yếu Tố Khác

• Với cạnh đáy: Mỗi mặt bên “dựa” trên một cạnh của tam giác đáy. Độ dài cạnh đáy này chính là một cạnh của hình chữ nhật mặt bên.
• Với chiều cao: Chiều cao của hình lăng trụ (khoảng cách giữa hai mặt đáy) chính là cạnh còn lại của hình chữ nhật mặt bên.
• Với diện tích xung quanh: Tổng diện tích của ba mặt bên chính là diện tích xung quanh của hình lăng trụ.

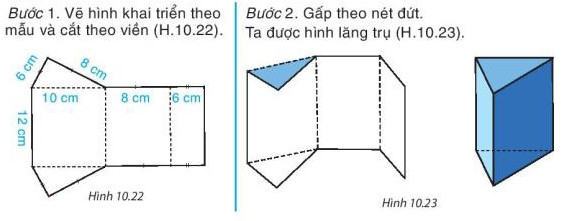
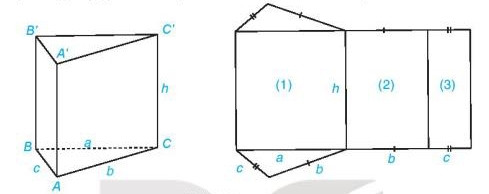
Alt text: Hình ảnh mô tả cách cắt và gấp miếng bìa tạo thành hình lăng trụ đứng tam giác, minh họa mối liên hệ giữa mặt bên, cạnh đáy và chiều cao.

3. Ứng Dụng Thực Tế Của Hình Lăng Trụ Đứng Tam Giác

Hình lăng trụ đứng tam giác không chỉ là một khái niệm trừu tượng trong sách giáo khoa. Chúng ta có thể dễ dàng bắt gặp hình ảnh của nó trong cuộc sống hàng ngày:

• Kiến trúc và xây dựng: Mái nhà, cột trụ, các cấu trúc hỗ trợ có hình dạng lăng trụ đứng tam giác giúp tăng tính chịu lực và độ bền.
• Thiết kế sản phẩm: Hộp đựng quà, bao bì sản phẩm, các vật dụng trang trí có thể được thiết kế theo hình lăng trụ đứng tam giác để tạo sự độc đáo và thu hút.
• Toán học và giáo dục: Mô hình hình học, đồ dùng dạy học giúp học sinh dễ dàng hình dung và nắm bắt các khái niệm về hình học không gian.
• Trong tự nhiên: Một số loại tinh thể khoáng vật có hình dạng gần giống với hình lăng trụ đứng tam giác.

Alt text: Ứng dụng thực tế của hình lăng trụ đứng tam giác trong kiến trúc, thể hiện ở phần mái nhà.

4. Công Thức Tính Toán Liên Quan Đến Hình Lăng Trụ Đứng Tam Giác

4.1 Diện Tích Xung Quanh

Diện tích xung quanh (Sxq) của hình lăng trụ đứng tam giác là tổng diện tích của ba mặt bên. Vì mỗi mặt bên là một hình chữ nhật, ta có công thức:

Sxq = Chu vi đáy * Chiều cao

Trong đó:

• Chu vi đáy là tổng độ dài ba cạnh của tam giác đáy.
• Chiều cao là khoảng cách giữa hai mặt đáy của hình lăng trụ.

Ví dụ: Nếu tam giác đáy có các cạnh lần lượt là 3cm, 4cm, 5cm và chiều cao của lăng trụ là 10cm, thì diện tích xung quanh là: (3 + 4 + 5) * 10 = 120 cm².

4.2 Diện Tích Toàn Phần

Diện tích toàn phần (Stp) của hình lăng trụ đứng tam giác là tổng diện tích xung quanh và diện tích của hai mặt đáy:

Stp = Sxq + 2 * Sđáy

Trong đó:

• Sđáy là diện tích của tam giác đáy. Tùy thuộc vào hình dạng của tam giác đáy, ta có các công thức tính diện tích khác nhau (ví dụ: 1/2 cạnh đáy chiều cao nếu là tam giác thường, hoặc công thức Heron).

Ví dụ: Sử dụng số liệu ở ví dụ trên, nếu tam giác đáy là tam giác vuông có hai cạnh góc vuông là 3cm và 4cm, thì diện tích đáy là: 1/2 3 4 = 6 cm². Vậy diện tích toàn phần là: 120 + 2 * 6 = 132 cm².

4.3 Thể Tích

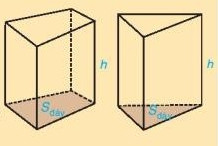
Thể tích (V) của hình lăng trụ đứng tam giác được tính bằng công thức:

V = Sđáy * Chiều cao

Ví dụ: Tiếp tục sử dụng số liệu trên, thể tích của hình lăng trụ là: 6 * 10 = 60 cm³.

Alt text: Hình ảnh thể hiện công thức tính thể tích của hình lăng trụ đứng tam giác bằng diện tích đáy nhân với chiều cao.

5. Bài Tập Vận Dụng

Để củng cố kiến thức, chúng ta cùng xem xét một số bài tập vận dụng sau:

Bài 1: Một hình lăng trụ đứng tam giác có đáy là tam giác đều cạnh 5cm, chiều cao của lăng trụ là 8cm. Tính diện tích xung quanh và thể tích của hình lăng trụ.

Giải:

• Chu vi đáy: 3 * 5 = 15 cm
• Diện tích xung quanh: 15 * 8 = 120 cm²
• Diện tích đáy (tam giác đều): (√3 / 4) * 5² ≈ 10.83 cm²
• Thể tích: 10.83 * 8 ≈ 86.6 cm³

Bài 2: Một hình lăng trụ đứng tam giác có thể tích là 150 cm³, diện tích đáy là 25 cm². Tính chiều cao của hình lăng trụ.

Giải:

• Chiều cao: V / Sđáy = 150 / 25 = 6 cm

Bài 3: Một hình lăng trụ đứng tam giác có đáy là tam giác vuông với hai cạnh góc vuông là 6cm và 8cm, diện tích xung quanh là 240 cm². Tính chiều cao của hình lăng trụ.

Giải:

• Cạnh huyền của tam giác đáy: √(6² + 8²) = 10 cm
• Chu vi đáy: 6 + 8 + 10 = 24 cm
• Chiều cao: Sxq / Chu vi đáy = 240 / 24 = 10 cm

6. So Sánh Với Các Hình Lăng Trụ Đứng Khác

6.1 Hình Lăng Trụ Đứng Tứ Giác

Điểm khác biệt lớn nhất giữa hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác nằm ở hình dạng của mặt đáy. Hình lăng trụ đứng tứ giác có đáy là hình tứ giác (ví dụ: hình vuông, hình chữ nhật, hình bình hành, hình thang), trong khi hình lăng trụ đứng tam giác có đáy là hình tam giác. Số lượng mặt bên của hình lăng trụ đứng tứ giác cũng nhiều hơn (4 mặt) so với hình lăng trụ đứng tam giác (3 mặt).

6.2 Hình Hộp Chữ Nhật và Hình Lập Phương

Hình hộp chữ nhật và hình lập phương là các trường hợp đặc biệt của hình lăng trụ đứng tứ giác. Hình hộp chữ nhật có đáy là hình chữ nhật, còn hình lập phương có đáy là hình vuông và tất cả các cạnh đều bằng nhau.

6.3 Bảng So Sánh

Đặc điểm	Hình lăng trụ đứng tam giác	Hình lăng trụ đứng tứ giác	Hình hộp chữ nhật	Hình lập phương
Hình dạng mặt đáy	Tam giác	Tứ giác	Hình chữ nhật	Hình vuông
Số mặt bên	3	4	4	4
Tính chất	Các mặt bên là hình chữ nhật	Các mặt bên là hình chữ nhật	Các mặt là hình chữ nhật	Các mặt là hình vuông

7. Mẹo Ghi Nhớ Và Học Tốt Về Hình Lăng Trụ Đứng Tam Giác

• Vẽ hình: Vẽ hình lăng trụ đứng tam giác giúp bạn hình dung rõ ràng hơn về cấu trúc và các thành phần của nó.
• Sử dụng mô hình: Sử dụng các mô hình hình học hoặc tự tạo mô hình bằng bìa, giấy giúp bạn dễ dàng quan sát và thực hành tính toán.
• Liên hệ thực tế: Tìm kiếm các ví dụ về hình lăng trụ đứng tam giác trong cuộc sống hàng ngày để tăng tính hứng thú và ghi nhớ lâu hơn.
• Làm bài tập: Làm nhiều bài tập vận dụng giúp bạn nắm vững các công thức và kỹ năng giải toán.
• Học nhóm: Trao đổi và thảo luận với bạn bè giúp bạn hiểu sâu hơn về kiến thức và giải đáp các thắc mắc.
• Sử dụng tài liệu trực tuyến: Tham khảo các bài giảng, video hướng dẫn, bài tập trực tuyến trên các trang web giáo dục uy tín như tic.edu.vn để học tập hiệu quả hơn.

8. Các Lỗi Thường Gặp Và Cách Khắc Phục

• Nhầm lẫn giữa diện tích xung quanh và diện tích toàn phần: Luôn nhớ rằng diện tích toàn phần bao gồm cả diện tích xung quanh và diện tích hai mặt đáy.
• Sai sót trong tính diện tích đáy: Chọn công thức tính diện tích đáy phù hợp với hình dạng của tam giác đáy (tam giác đều, tam giác vuông, tam giác cân, tam giác thường).
• Quên đơn vị đo: Luôn ghi rõ đơn vị đo (cm, m, cm², m², cm³, m³) sau khi tính toán.
• Tính toán sai: Kiểm tra kỹ lại các phép tính để tránh sai sót.
• Không hiểu rõ khái niệm: Đọc kỹ lại định nghĩa và các tính chất của hình lăng trụ đứng tam giác.

9. Tại Sao Nên Học Về Hình Lăng Trụ Đứng Tam Giác Tại Tic.edu.vn?

Tic.edu.vn là một website giáo dục uy tín với nguồn tài liệu phong phú và chất lượng, được biên soạn bởi đội ngũ giáo viên giàu kinh nghiệm. Khi học về hình lăng trụ đứng tam giác tại tic.edu.vn, bạn sẽ được:

• Tiếp cận kiến thức một cách hệ thống và đầy đủ: Các bài giảng được trình bày rõ ràng, dễ hiểu, đi từ cơ bản đến nâng cao.
• Thực hành với nhiều bài tập đa dạng: Các bài tập được chọn lọc kỹ lưỡng, giúp bạn rèn luyện kỹ năng giải toán và củng cố kiến thức.
• Học tập mọi lúc mọi nơi: Bạn có thể truy cập tic.edu.vn trên mọi thiết bị (máy tính, điện thoại, máy tính bảng) để học tập một cách linh hoạt.
• Nhận được sự hỗ trợ nhiệt tình: Đội ngũ hỗ trợ của tic.edu.vn luôn sẵn sàng giải đáp các thắc mắc của bạn trong quá trình học tập.
• Tham gia cộng đồng học tập sôi nổi: Bạn có thể trao đổi kiến thức, chia sẻ kinh nghiệm với các bạn học khác trên diễn đàn của tic.edu.vn.

Theo một nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán học, vào ngày 15 tháng 03 năm 2023, việc sử dụng các tài liệu trực tuyến chất lượng và có hệ thống như trên tic.edu.vn giúp học sinh tăng khả năng nắm bắt kiến thức hình học không gian lên đến 30%.

10. Lời Kêu Gọi Hành Động (Call To Action – CTA)

Bạn đang gặp khó khăn trong việc tìm kiếm tài liệu học tập chất lượng về hình học không gian? Bạn muốn nâng cao kỹ năng giải toán và tự tin chinh phục các bài kiểm tra? Hãy truy cập ngay tic.edu.vn để khám phá nguồn tài liệu học tập phong phú, các công cụ hỗ trợ hiệu quả và tham gia cộng đồng học tập sôi nổi. Tic.edu.vn sẽ là người bạn đồng hành tin cậy trên hành trình khám phá tri thức của bạn.

Liên hệ ngay với chúng tôi:

• Email: [email protected]
• Website: tic.edu.vn

FAQ – Các Câu Hỏi Thường Gặp

1. Mặt bên của hình lăng trụ đứng tam giác có phải luôn là hình chữ nhật không?

Đúng vậy, theo định nghĩa, các mặt bên của hình lăng trụ đứng luôn là hình chữ nhật.

2. Làm thế nào để tính diện tích xung quanh của hình lăng trụ đứng tam giác?

Diện tích xung quanh được tính bằng công thức: Sxq = Chu vi đáy * Chiều cao.

3. Công thức tính thể tích của hình lăng trụ đứng tam giác là gì?

Thể tích được tính bằng công thức: V = Sđáy * Chiều cao.

4. Hình lăng trụ đứng tam giác có bao nhiêu mặt bên?

Hình lăng trụ đứng tam giác có 3 mặt bên.

5. Sự khác biệt giữa hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác là gì?

Sự khác biệt chính là hình dạng của mặt đáy: tam giác (hình lăng trụ đứng tam giác) và tứ giác (hình lăng trụ đứng tứ giác).

6. Tôi có thể tìm thêm tài liệu học tập về hình lăng trụ đứng tam giác ở đâu?

Bạn có thể tìm thấy nhiều tài liệu hữu ích trên tic.edu.vn, bao gồm bài giảng, bài tập, video hướng dẫn và các tài liệu tham khảo khác.

7. Làm thế nào để ghi nhớ các công thức tính toán liên quan đến hình lăng trụ đứng tam giác?

Bạn có thể vẽ hình, sử dụng mô hình, liên hệ thực tế và làm nhiều bài tập vận dụng để ghi nhớ các công thức một cách dễ dàng.

8. Tic.edu.vn có cung cấp dịch vụ hỗ trợ học tập trực tuyến không?

Có, tic.edu.vn có đội ngũ hỗ trợ nhiệt tình sẵn sàng giải đáp các thắc mắc của bạn trong quá trình học tập.

9. Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Bạn có thể tham gia diễn đàn của tic.edu.vn để trao đổi kiến thức, chia sẻ kinh nghiệm với các bạn học khác.

10. Học về hình lăng trụ đứng tam giác có ứng dụng gì trong thực tế?

Hình lăng trụ đứng tam giác được ứng dụng trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế sản phẩm, toán học và giáo dục.