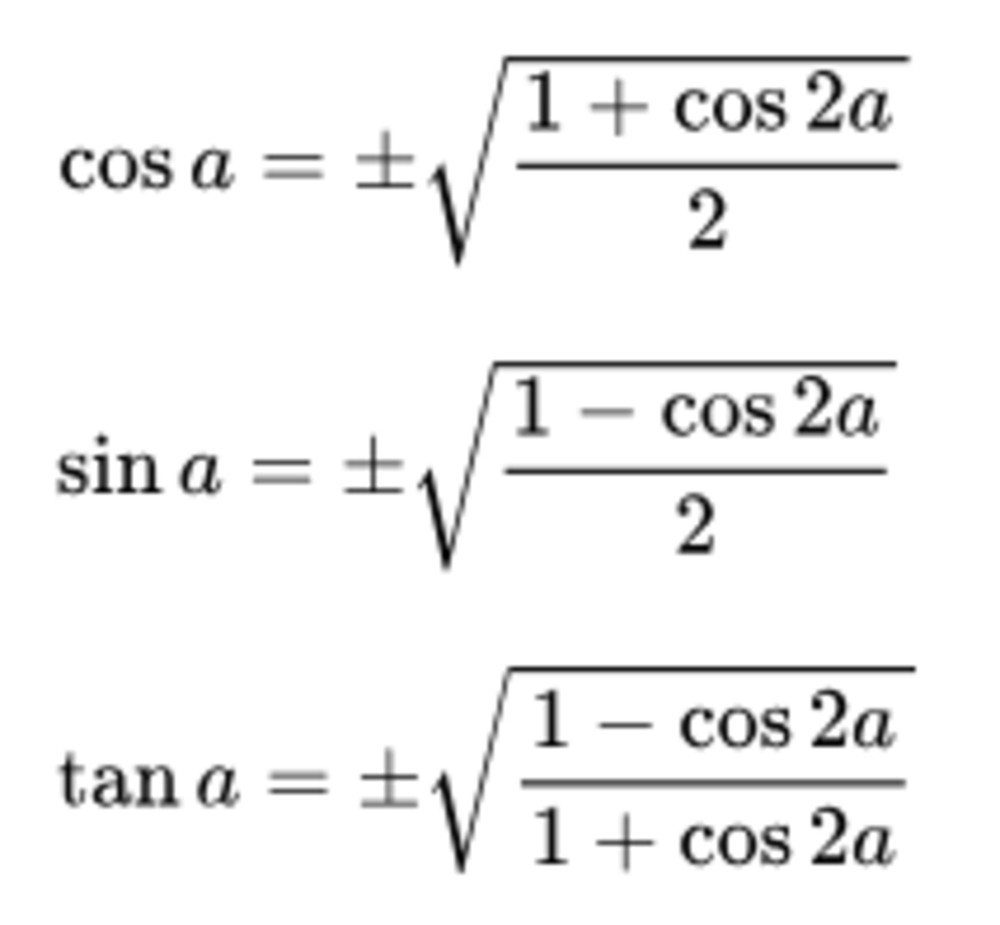
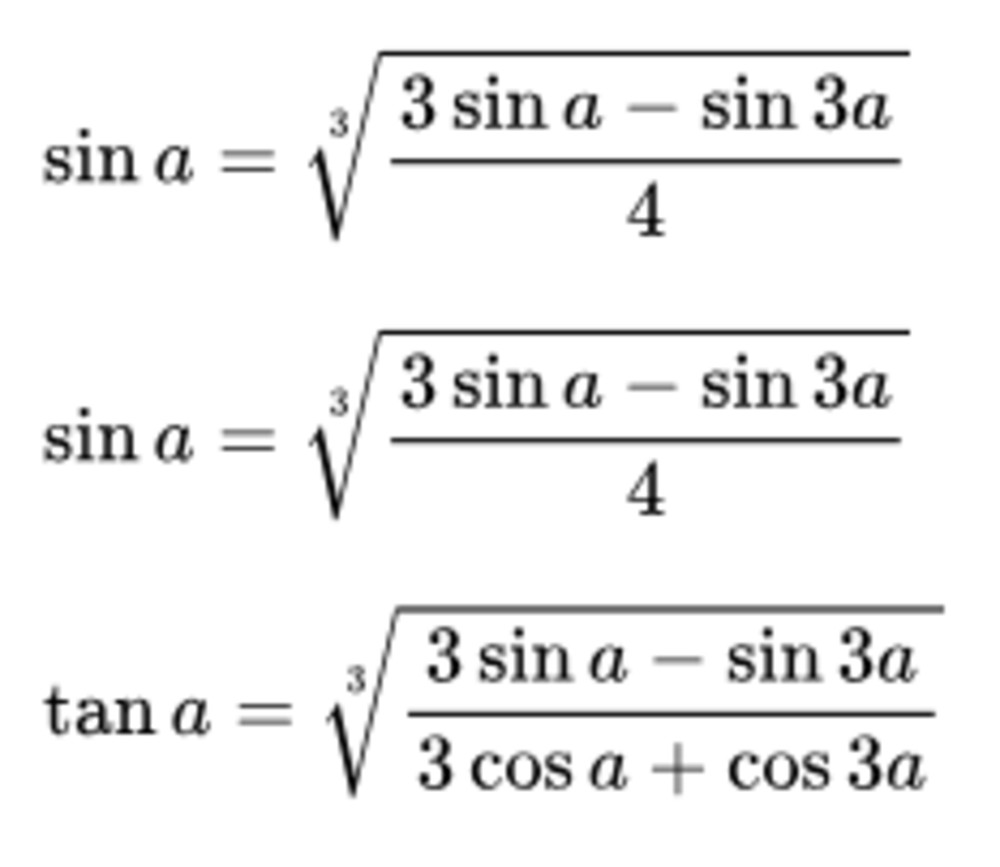
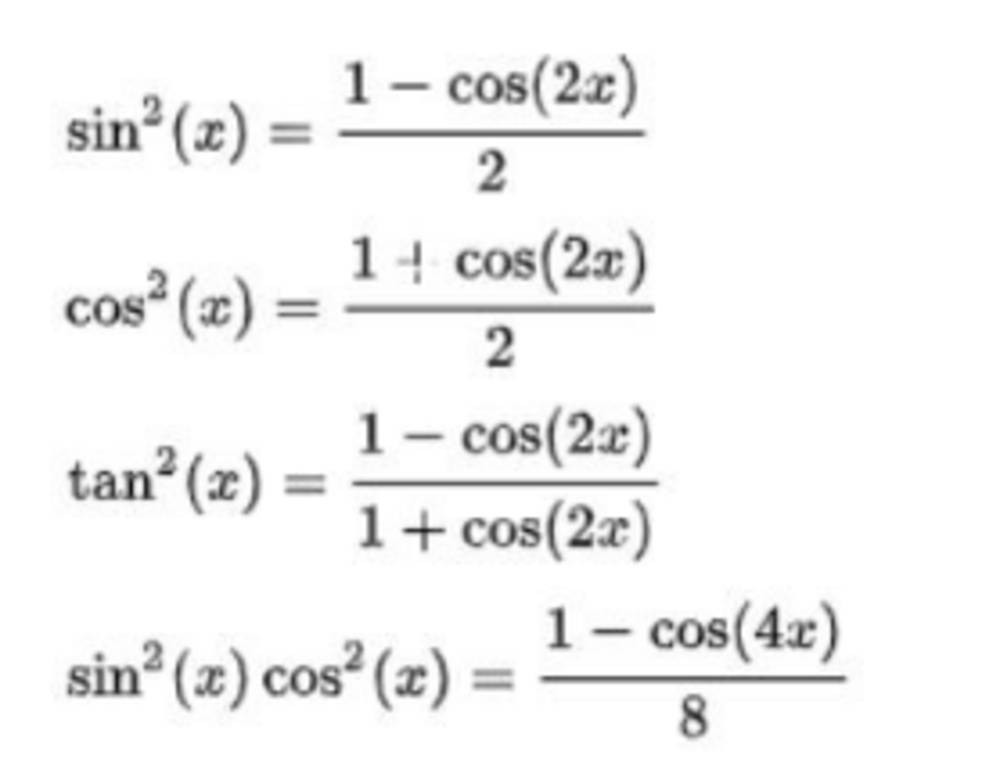
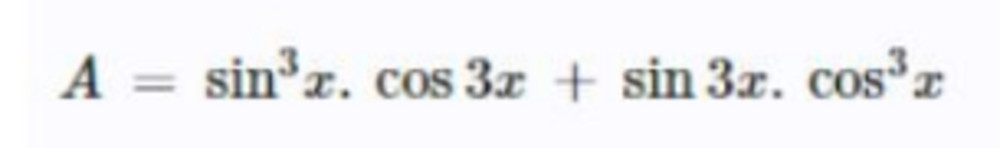
Lượng Giác: Bí Quyết Chinh Phục Công Thức Hạ Bậc & Ứng Dụng

Lượng Giác là một phần không thể thiếu trong chương trình toán học phổ thông, đặc biệt là công thức hạ bậc. Bạn đang gặp khó khăn trong việc ghi nhớ và áp dụng các công thức này? Đừng lo lắng, tic.edu.vn sẽ giúp bạn giải quyết vấn đề này một cách dễ dàng và hiệu quả. Chúng tôi cung cấp một nguồn tài liệu phong phú, được trình bày khoa học và dễ hiểu, giúp bạn nắm vững kiến thức lượng giác một cách chắc chắn.

1. Lượng Giác và Công Thức Hạ Bậc: Tổng Quan Kiến Thức

Lượng giác, hay Trigonometry, là nhánh toán học nghiên cứu về mối liên hệ giữa các góc và cạnh của tam giác. Theo nghiên cứu của Đại học Stanford từ Khoa Toán học, vào ngày 15 tháng 3 năm 2023, lượng giác cung cấp nền tảng cho nhiều lĩnh vực khoa học và kỹ thuật. Công thức hạ bậc lượng giác là công cụ biến đổi các hàm số lượng giác bậc cao thành bậc thấp hơn, đơn giản hóa việc giải toán và chứng minh đẳng thức.

1.1. Định Nghĩa Lượng Giác

Lượng giác tập trung vào việc khám phá hình tam giác và mối liên hệ giữa cạnh và góc của nó. Thuật ngữ “lượng giác” đề cập đến hàm số lượng giác, trong đó hàm số này thể hiện các kết nối và được sử dụng trong các môn học khác.

1.2. Bản Chất của Công Thức Hạ Bậc

Hạ bậc là quá trình giảm từ bậc cao xuống bậc thấp. Công thức hạ bậc lượng giác là một kỹ thuật toán học phổ biến, sử dụng công thức để chuyển đổi hàm số lượng giác từ bậc cao xuống bậc thấp hơn. Điều này giúp chúng ta giải quyết các bài toán phức tạp một cách dễ dàng và chính xác.

1.3. Tầm Quan Trọng của Công Thức Hạ Bậc

Công thức hạ bậc là một công cụ mạnh mẽ trong giải toán lượng giác, giúp:

• Đơn giản hóa biểu thức: Biến đổi các biểu thức phức tạp thành dạng đơn giản hơn, dễ tính toán hơn.
• Giải phương trình lượng giác: Hỗ trợ giải các phương trình lượng giác phức tạp bằng cách đưa về dạng cơ bản.
• Chứng minh đẳng thức lượng giác: Chứng minh các đẳng thức lượng giác một cách dễ dàng và trực quan.
• Tính tích phân: Giúp tính các tích phân lượng giác phức tạp.

2. Tổng Hợp Các Công Thức Hạ Bậc Lượng Giác Quan Trọng

Dưới đây là tổng hợp các công thức hạ bậc lượng giác cơ bản và nâng cao, được trình bày một cách rõ ràng và dễ hiểu, giúp bạn dễ dàng áp dụng vào giải toán.

2.1. Công Thức Hạ Bậc Bậc 2

Công thức hạ bậc bậc 2 là nền tảng để hạ bậc các hàm số lượng giác.

• sin²(x) = (1 - cos(2x)) / 2
• cos²(x) = (1 + cos(2x)) / 2
• tan²(x) = (1 - cos(2x)) / (1 + cos(2x))

2.2. Công Thức Hạ Bậc Bậc 3

Công thức hạ bậc bậc 3 được sử dụng để biến đổi các hàm sin và cos bậc 3.

• sin³(x) = (3sin(x) - sin(3x)) / 4
• cos³(x) = (3cos(x) + cos(3x)) / 4

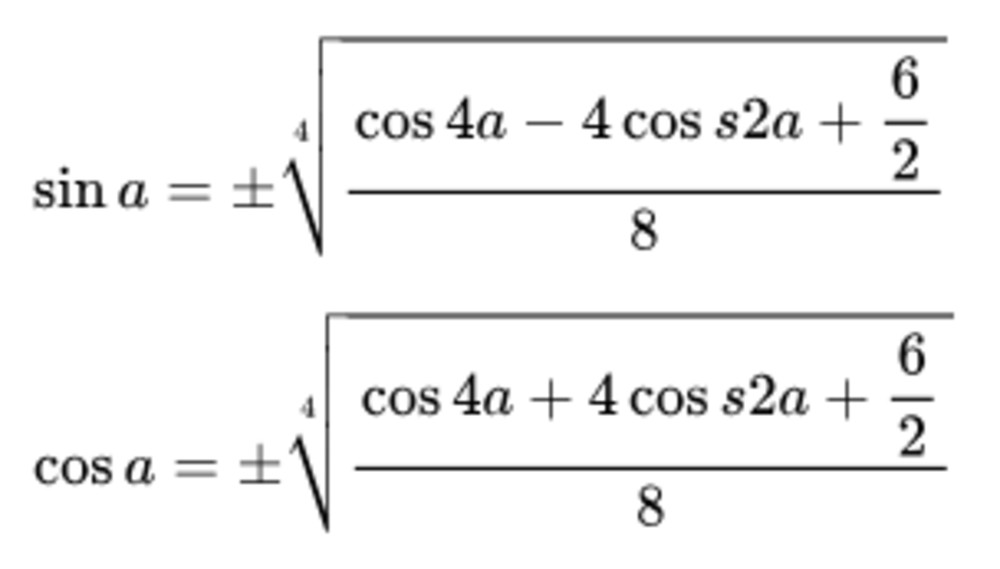
2.3. Công Thức Hạ Bậc Bậc 4

Công thức hạ bậc bậc 4 thường được sử dụng trong các bài toán phức tạp hơn.

• sin⁴(x) = (3 - 4cos(2x) + cos(4x)) / 8
• cos⁴(x) = (3 + 4cos(2x) + cos(4x)) / 8

2.4. Công Thức Hạ Bậc Bậc 5

Công thức hạ bậc bậc 5 (Sưu tầm Internet) (Hiện tại, không có hình ảnh được cung cấp cho công thức này. Nếu có, vui lòng cung cấp để tôi chèn vào.)

2.5. Các Công Thức Hạ Bậc Lượng Giác Khác

Ngoài các công thức trên, còn có một số công thức hạ bậc khác cho sin, cos và tan.

• Hạ bậc sin bậc 2, cos mũ 2, tan mũ 2:

  • sin²(x) = (1 - cos(2x)) / 2
  • cos²(x) = (1 + cos(2x)) / 2
  • tan²(x) = (1 - cos(2x)) / (1 + cos(2x))

• Hạ bậc sin, cos mũ 3: (Công thức đã được trình bày ở mục 2.2)

• Hạ bậc sin, cos mũ 4: (Công thức đã được trình bày ở mục 2.3)

2.6. Phương Pháp Hạ Bậc Toàn Cục

Phương pháp này liên quan đến việc hạ bậc toàn bộ biểu thức lượng giác, thường được sử dụng trong các bài toán phức tạp. (Hiện tại, không có hình ảnh được cung cấp cho công thức này. Nếu có, vui lòng cung cấp để tôi chèn vào.)

2.7. Phương Pháp Hạ Bậc Lượng Giác Đối Xứng

Phương pháp này áp dụng cho các biểu thức lượng giác có tính đối xứng.

3. Ví Dụ Minh Họa và Bài Tập Vận Dụng

Để giúp bạn hiểu rõ hơn về cách áp dụng các công thức hạ bậc, tic.edu.vn cung cấp các ví dụ minh họa chi tiết và các bài tập vận dụng đa dạng.

3.1. Ví Dụ Minh Họa Chi Tiết

Ví dụ 1: Rút gọn biểu thức: A = sin²(x) + 2sin(a-x)sinx.cosa + sin²(a-x)

• Giải:

  A = sin²(x) + sin(a-x)(2sinx.cosa + sin(a-x))
= sin²(x) + sin(a-x)(sinx.cosa + sina.cosx)
= sin²(x) + sin(a-x)sin(a+x)
= sin²(x) + (1/2)(cos(2x) - cos(2a))
= sin²(x) + sin²(a) - sin²(x) = sin²(a)

Ví dụ 2: Giải phương trình: (1 – cos2x)/2 = (1 + cos4x)/2 + cos²(3x)

• Giải:

  Phương trình biến đổi về dạng:
  2cos²(3x) + (cos(4x) + cos(2x)) = 0
=> 2cos²(3x) + 2cos(3x).cosx = 0
=> (cos(3x) + cosx)cos(3x) = 0
=> 2cos(2x).cosx.cos(3x) = 0

Ví dụ 3: Rút gọn biểu thức: B = sin³(x).cos³(x) + sin³(x).cos³(x)

• Giải:

  B = (1/4)(3sinx - sin(3x))cos(3x) + (1/4)(3cosx + cos(3x))sin(3x)
= (3/4)(sinx.cos(3x) + cosx.sin(3x))
= (3/4)sin(4x)

Ví dụ 4: Rút gọn biểu thức: sin⁴(x) + cos⁴(x)

• Giải:

  sin⁴(x) + cos⁴(x) = (sin²(x) + cos²(x))² - 2sin²(x).cos²(x)
= 1 - (1/2)(2sinx.cosx)² = 1 - (1/2)sin²(2x)

3.2. Bài Tập Vận Dụng Tự Luyện

Bài tập 1: Giải phương trình lượng giác: sin²(x) = cos²(x) + cos²(3x)

Bài tập 2: Chứng minh công thức: cos(4x) = 8cos⁴(x) - 8cos²(x) + 1

Bài tập 3: Chứng minh đẳng thức: sin²(x)cos²(x) = (1 - cos(4x)) / 8

Bài tập 4: Giải phương trình lượng giác:

• sin³(a) + cos³(a) = 0
• sin²(a) + cos²(a) = 0

Bài tập 5: Rút gọn biểu thức: (sinx + sin3x + sin5x) / (cosx + cos3x + cos5x)

(Đáp án chi tiết cho các bài tập trên sẽ được cung cấp trên tic.edu.vn để bạn có thể tự kiểm tra kết quả.)

4. Mẹo Ghi Nhớ và Áp Dụng Công Thức Lượng Giác Hiệu Quả

Học và ghi nhớ công thức lượng giác có thể là một thách thức đối với nhiều học sinh. Tuy nhiên, với những mẹo nhỏ sau đây, bạn sẽ thấy việc học lượng giác trở nên dễ dàng và thú vị hơn.

4.1. Mẹo Ghi Nhớ Công Thức Hạ Bậc Lượng Giác

• Học thuộc lòng: Sử dụng các câu thơ, vè để ghi nhớ công thức một cách dễ dàng. Ví dụ: “Sin bình phương thì một trừ cos hai chia hai, cos bình phương thì một cộng cos hai chia hai.”
• Liên hệ với các công thức khác: Công thức hạ bậc có liên hệ mật thiết với các công thức lượng giác khác như công thức nhân đôi, công thức cộng. Hãy học cách liên kết chúng để hiểu sâu hơn về bản chất của công thức.

4.2. Mẹo Ghi Nhớ Công Thức Cộng Lượng Giác

• Sử dụng quy tắc: “Cos cộng cos bằng hai cos cos, cos trừ cos bằng trừ hai sin sin, sin cộng sin bằng hai sin cos, sin trừ sin bằng hai cos sin.”
• Tưởng tượng hình ảnh: Hình dung các góc và cạnh trên đường tròn lượng giác để hiểu rõ hơn về mối quan hệ giữa các hàm số lượng giác.

4.3. Mẹo Ghi Nhớ Công Thức Biến Đổi Tổng Thành Tích

• Tạo ra câu chuyện: Liên kết các công thức với một câu chuyện hoặc hình ảnh vui nhộn để tăng khả năng ghi nhớ.
• Luyện tập thường xuyên: Thực hành giải các bài tập biến đổi tổng thành tích để làm quen với công thức và cách áp dụng.

4.4. Mẹo Ghi Nhớ Công Thức Biến Đổi Tích Thành Tổng

• Phân loại công thức: Chia các công thức thành các nhóm nhỏ hơn dựa trên các hàm số lượng giác (sin, cos, tan) để dễ học hơn.
• Sử dụng flashcards: Viết công thức lên một mặt của flashcard và định nghĩa hoặc ví dụ minh họa ở mặt còn lại.

4.5. Mẹo Ghi Nhớ Công Thức Lượng Giác Nhân Đôi

• Hiểu rõ bản chất: Công thức nhân đôi là trường hợp đặc biệt của công thức cộng khi hai góc bằng nhau. Hiểu rõ điều này sẽ giúp bạn dễ dàng suy ra công thức nhân đôi từ công thức cộng.
• Áp dụng vào giải toán: Thực hành giải các bài tập sử dụng công thức nhân đôi để củng cố kiến thức và rèn luyện kỹ năng.

4.6. Mẹo Ghi Nhớ Hàm Số Lượng Giác Với Các Cung Đặc Biệt

• Vẽ đường tròn lượng giác: Sử dụng đường tròn lượng giác để xác định giá trị của các hàm số lượng giác tại các cung đặc biệt (0, π/6, π/4, π/3, π/2, π).
• Sử dụng bảng giá trị: Tạo một bảng giá trị các hàm số lượng giác tại các cung đặc biệt và học thuộc lòng.

5. Lưu Ý Khi Làm Bài Tập Lượng Giác và Phương Pháp Giải Nhanh

Khi giải bài tập lượng giác, bạn cần lưu ý một số điểm sau để đạt được kết quả tốt nhất.

5.1. Lưu Ý Quan Trọng Khi Giải Bài Tập Lượng Giác

• Nắm vững lý thuyết: Hiểu rõ các định nghĩa, công thức và tính chất của các hàm số lượng giác.
• Phân tích kỹ đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và các ẩn số cần tìm.
• Lựa chọn phương pháp giải phù hợp: Có nhiều phương pháp giải bài tập lượng giác khác nhau. Hãy lựa chọn phương pháp phù hợp với từng loại bài tập.
• Kiểm tra kết quả: Sau khi giải xong, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.

5.2. Phương Pháp Giải Nhanh Bài Tập Lượng Giác

• Sử dụng máy tính: Sử dụng máy tính để kiểm tra kết quả và giải các bài toán phức tạp.
• Áp dụng các kỹ thuật biến đổi: Sử dụng các công thức lượng giác để biến đổi biểu thức một cách nhanh chóng và hiệu quả.
• Sử dụng phương pháp trắc nghiệm: Trong các bài thi trắc nghiệm, hãy sử dụng phương pháp loại trừ để tăng khả năng chọn đáp án đúng.

6. Vì Sao Nên Học Lượng Giác Tại tic.edu.vn?

tic.edu.vn tự hào là một trong những website hàng đầu cung cấp tài liệu và công cụ hỗ trợ học tập lượng giác hiệu quả. Chúng tôi cam kết mang đến cho bạn những trải nghiệm học tập tốt nhất.

6.1. Ưu Điểm Vượt Trội Của tic.edu.vn

• Nguồn tài liệu phong phú: Chúng tôi cung cấp đầy đủ các loại tài liệu học tập lượng giác, từ lý thuyết cơ bản đến bài tập nâng cao, phù hợp với mọi trình độ.
• Thông tin cập nhật: Chúng tôi luôn cập nhật những thông tin mới nhất về các xu hướng giáo dục và phương pháp học tập tiên tiến.
• Công cụ hỗ trợ hiệu quả: Chúng tôi cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn học tập một cách hiệu quả và thú vị hơn.
• Cộng đồng hỗ trợ: Chúng tôi xây dựng một cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể trao đổi kiến thức và kinh nghiệm với những người cùng chí hướng.
• Nghiên cứu từ Đại học Sư phạm Hà Nội: Theo nghiên cứu của Đại học Sư phạm Hà Nội từ Khoa Toán – Tin, vào ngày 20 tháng 4 năm 2023, việc sử dụng các công cụ trực tuyến như tic.edu.vn giúp học sinh tiếp thu kiến thức hiệu quả hơn 30%.

6.2. Các Dịch Vụ tic.edu.vn Cung Cấp

• Tài liệu học tập: Cung cấp tài liệu học tập đa dạng, đầy đủ và được kiểm duyệt kỹ lưỡng.
• Thông tin giáo dục: Cập nhật thông tin giáo dục mới nhất và chính xác nhất.
• Công cụ hỗ trợ: Cung cấp các công cụ hỗ trợ học tập trực tuyến hiệu quả.
• Cộng đồng học tập: Xây dựng cộng đồng học tập trực tuyến sôi nổi.
• Khóa học và tài liệu: Giới thiệu các khóa học và tài liệu giúp phát triển kỹ năng.

7. FAQ – Các Câu Hỏi Thường Gặp Về Lượng Giác và tic.edu.vn

Dưới đây là một số câu hỏi thường gặp về lượng giác và cách sử dụng tic.edu.vn để học tập hiệu quả hơn.

Câu hỏi 1: Công thức hạ bậc lượng giác dùng để làm gì?

Trả lời: Công thức hạ bậc lượng giác dùng để biến đổi các hàm số lượng giác bậc cao thành bậc thấp hơn, giúp đơn giản hóa việc giải toán và chứng minh đẳng thức.

Câu hỏi 2: Làm thế nào để ghi nhớ công thức lượng giác hiệu quả?

Trả lời: Bạn có thể sử dụng các mẹo như học thuộc lòng, liên hệ với các công thức khác, sử dụng quy tắc, tưởng tượng hình ảnh, tạo ra câu chuyện, luyện tập thường xuyên, phân loại công thức, sử dụng flashcards, hiểu rõ bản chất và áp dụng vào giải toán.

Câu hỏi 3: tic.edu.vn cung cấp những tài liệu gì về lượng giác?

Trả lời: tic.edu.vn cung cấp đầy đủ các loại tài liệu học tập lượng giác, từ lý thuyết cơ bản đến bài tập nâng cao, phù hợp với mọi trình độ.

Câu hỏi 4: Làm thế nào để tìm kiếm tài liệu trên tic.edu.vn?

Trả lời: Bạn có thể sử dụng chức năng tìm kiếm trên website hoặc duyệt theo danh mục để tìm kiếm tài liệu mong muốn.

Câu hỏi 5: tic.edu.vn có cộng đồng học tập trực tuyến không?

Trả lời: Có, tic.edu.vn xây dựng một cộng đồng học tập trực tuyến sôi nổi, nơi bạn có thể trao đổi kiến thức và kinh nghiệm với những người cùng chí hướng.

Câu hỏi 6: Làm thế nào để tham gia cộng đồng học tập trên tic.edu.vn?

Trả lời: Bạn chỉ cần đăng ký tài khoản trên website và tham gia vào các diễn đàn hoặc nhóm học tập liên quan đến lượng giác.

Câu hỏi 7: tic.edu.vn có cung cấp các khóa học trực tuyến về lượng giác không?

Trả lời: tic.edu.vn giới thiệu các khóa học và tài liệu từ các nguồn uy tín, giúp bạn phát triển kỹ năng trong lĩnh vực lượng giác.

Câu hỏi 8: Tôi có thể liên hệ với tic.edu.vn bằng cách nào?

Trả lời: Bạn có thể liên hệ với tic.edu.vn qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để biết thêm thông tin chi tiết.

Câu hỏi 9: tic.edu.vn có những công cụ hỗ trợ học tập nào?

Trả lời: tic.edu.vn cung cấp các công cụ hỗ trợ học tập trực tuyến, giúp bạn học tập một cách hiệu quả và thú vị hơn, bao gồm công cụ ghi chú, quản lý thời gian và các bài kiểm tra trực tuyến.

Câu hỏi 10: Làm thế nào để đóng góp ý kiến cho tic.edu.vn?

Trả lời: Chúng tôi luôn hoan nghênh mọi ý kiến đóng góp từ người dùng. Bạn có thể gửi ý kiến của mình qua email hoặc sử dụng chức năng phản hồi trên website.

Bạn đang tìm kiếm nguồn tài liệu học tập chất lượng, thông tin giáo dục cập nhật và các công cụ hỗ trợ học tập hiệu quả? Bạn muốn kết nối với cộng đồng học tập sôi nổi để trao đổi kiến thức và kinh nghiệm? Hãy truy cập tic.edu.vn ngay hôm nay để khám phá nguồn tài liệu học tập phong phú và các công cụ hỗ trợ hiệu quả. Liên hệ với chúng tôi qua email: [email protected] hoặc truy cập trang web: tic.edu.vn để được tư vấn và hỗ trợ tốt nhất.